Pflichtteil 1
Aufgabe 1
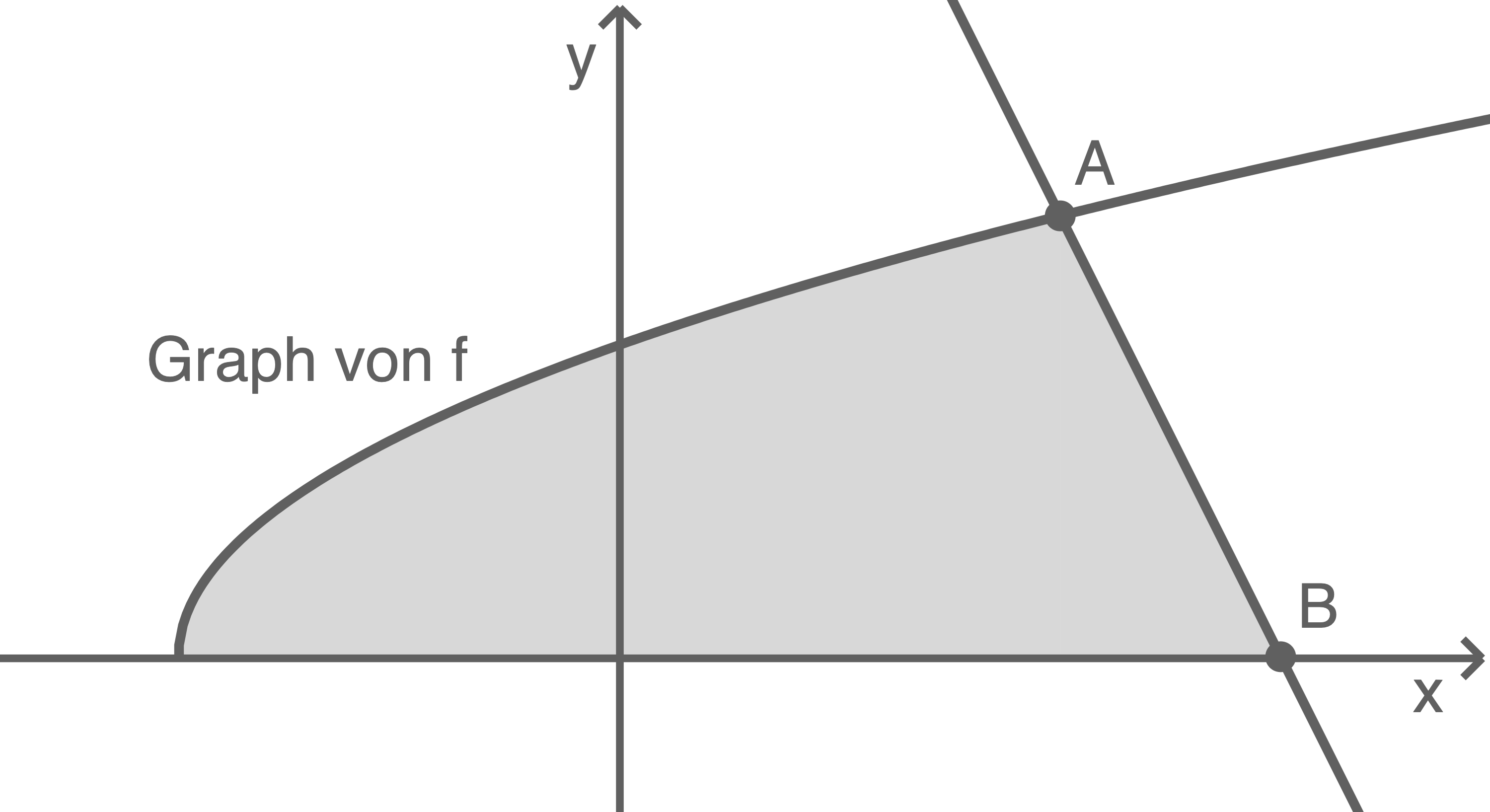
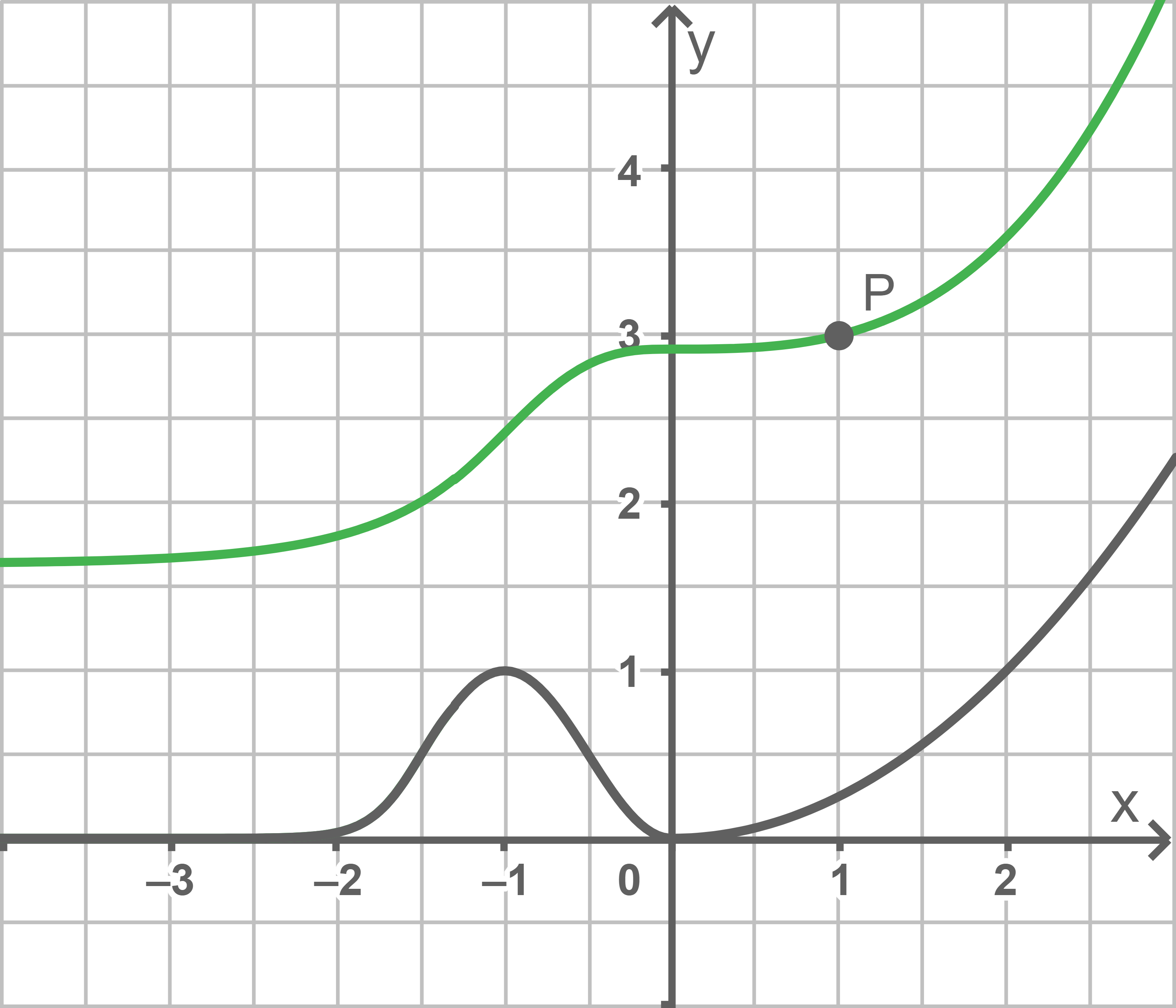
Die Abbildung zeigt den Graphen der Funktion  mit
mit  und die Gerade durch die Punkte
und die Gerade durch die Punkte  und
und 
a)
Gib die maximale Definitionsmenge der Funktion  an.
an.
(0,5 VP)
b)
Bestimme den Inhalt der markierten Fläche.
(2 VP)
Aufgabe 2
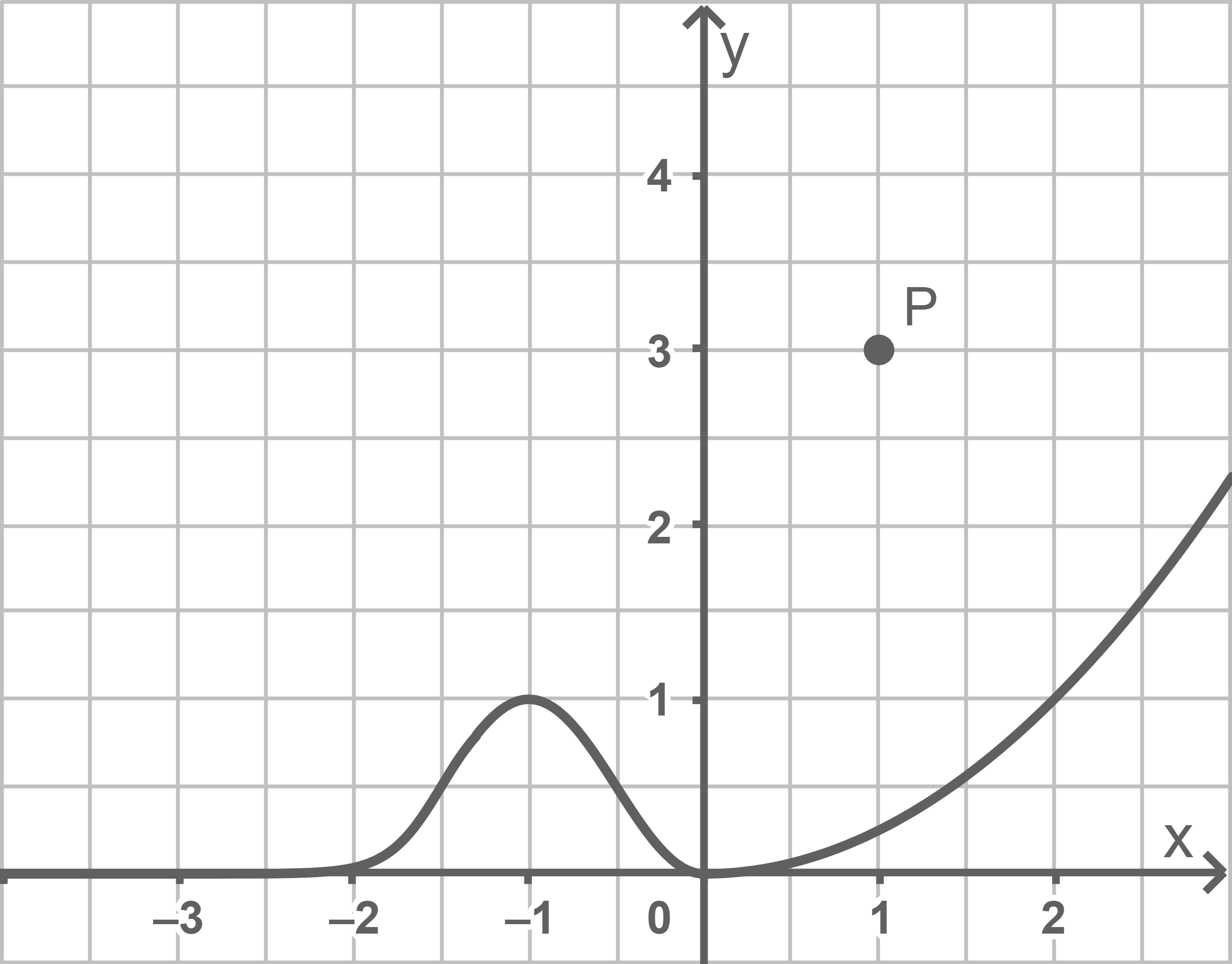
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion  , dessen einzige Extrempunkte
, dessen einzige Extrempunkte  und
und  sind, sowie den Punkt
sind, sowie den Punkt 
a)
Gib die Koordinaten des Tiefpunkts des Graphen der in  definierten Funktion
definierten Funktion  mit
mit  an.
an.
(1 VP)
b)
Der Graph einer Stammfunktion von  verläuft durch
verläuft durch  Skizziere diesen Graphen in der Abbildung.
Skizziere diesen Graphen in der Abbildung.
(1,5 VP)
Aufgabe 3
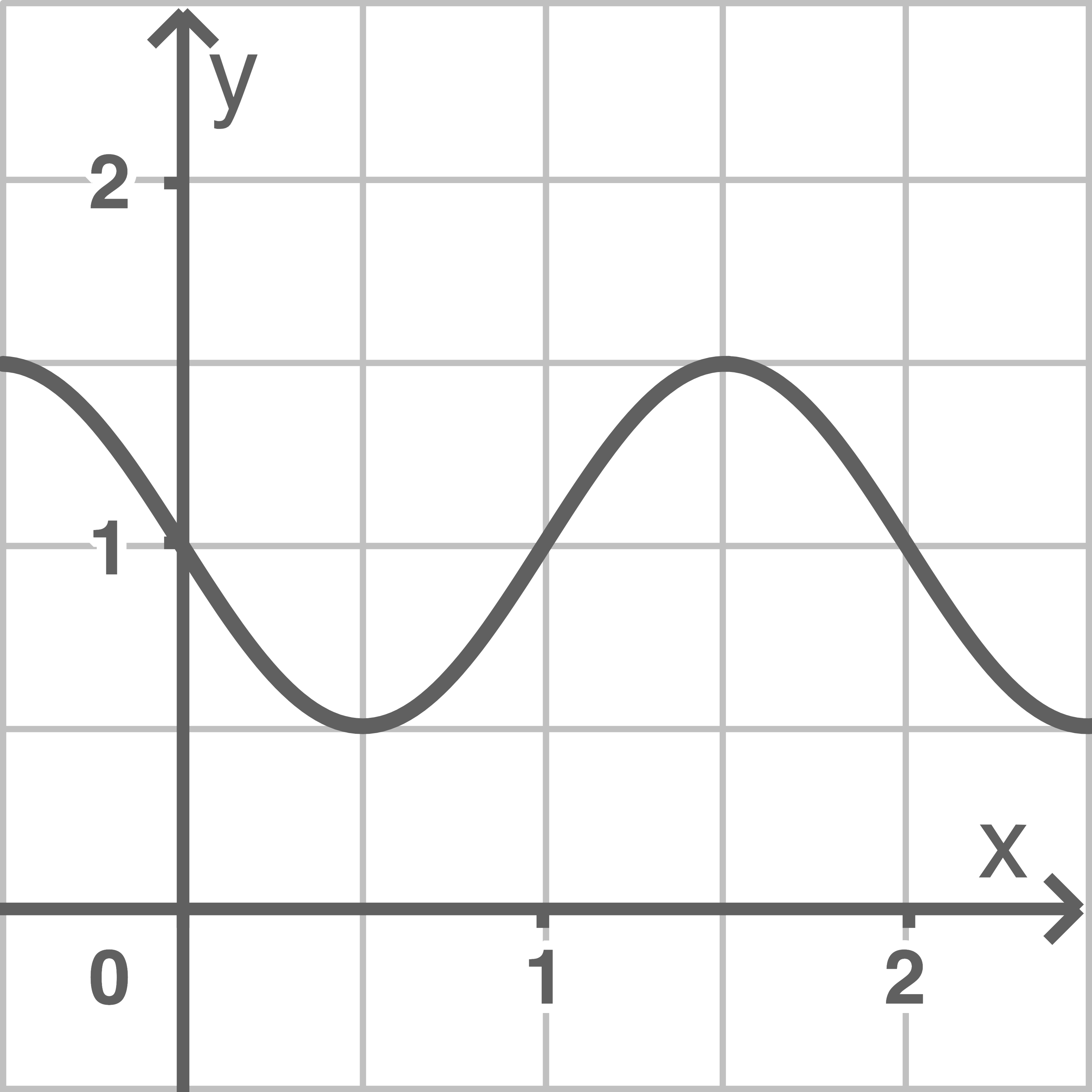
Die Abbildung zeigt den Graphen einer in  definierten Funktion
definierten Funktion 
a)
Beurteile die folgende Aussage:
„Für jeden Wert von  mit
mit  ist die Steigung des Graphen von
ist die Steigung des Graphen von  kleiner als 3.“
kleiner als 3.“
(1 VP)
b)
Mit dem Term  kann das Volumen eines Körpers berechnet werden.
Begründe, dass dieses Volumen größer als
kann das Volumen eines Körpers berechnet werden.
Begründe, dass dieses Volumen größer als  ist.
ist.
(1,5 VP)
Aufgabe 4
Gegeben ist die Gerade
a)
Zeige, dass  in der Ebene
in der Ebene  liegt.
liegt.
(1 VP)
b)
Gegeben ist außerdem die Schar der Geraden  mit
mit  und
und  .
Weise nach, dass
.
Weise nach, dass  und
und  für jeden Wert von
für jeden Wert von  windschief sind.
windschief sind.
(1,5 VP)
Aufgabe 5
Gegeben sind die Geraden
a)
Begründe, dass  und
und  nicht identisch sind.
nicht identisch sind.
(0,5 VP)
b)
Die Gerade  soll durch Spiegelung an einer Ebene auf die Gerade
soll durch Spiegelung an einer Ebene auf die Gerade  abgebildet werden.
Bestimme eine Gleichung einer geeigneten Ebene und erläutere das Vorgehen.
abgebildet werden.
Bestimme eine Gleichung einer geeigneten Ebene und erläutere das Vorgehen.
(2 VP)
Aufgabe 6
In einem Behälter befinden sich fünf Kugeln, auf denen jeweils eine Zahl steht. Auf drei der Kugeln steht die Zahl 2, auf zwei der Kugeln die negative Zahl
a)
Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term  berechnet werden kann.
berechnet werden kann.
(0,5 VP)
b)
Die Zufallsgröße  gibt das Produkt der Zahlen an, die auf den beiden entnommenen Kugeln stehen. Der Erwartungswert von
gibt das Produkt der Zahlen an, die auf den beiden entnommenen Kugeln stehen. Der Erwartungswert von  ist 4.
Bestimme den Wert von
ist 4.
Bestimme den Wert von 
(2 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Der Radikand nimmt keine negativen Werte an. Somit folgt:

b)
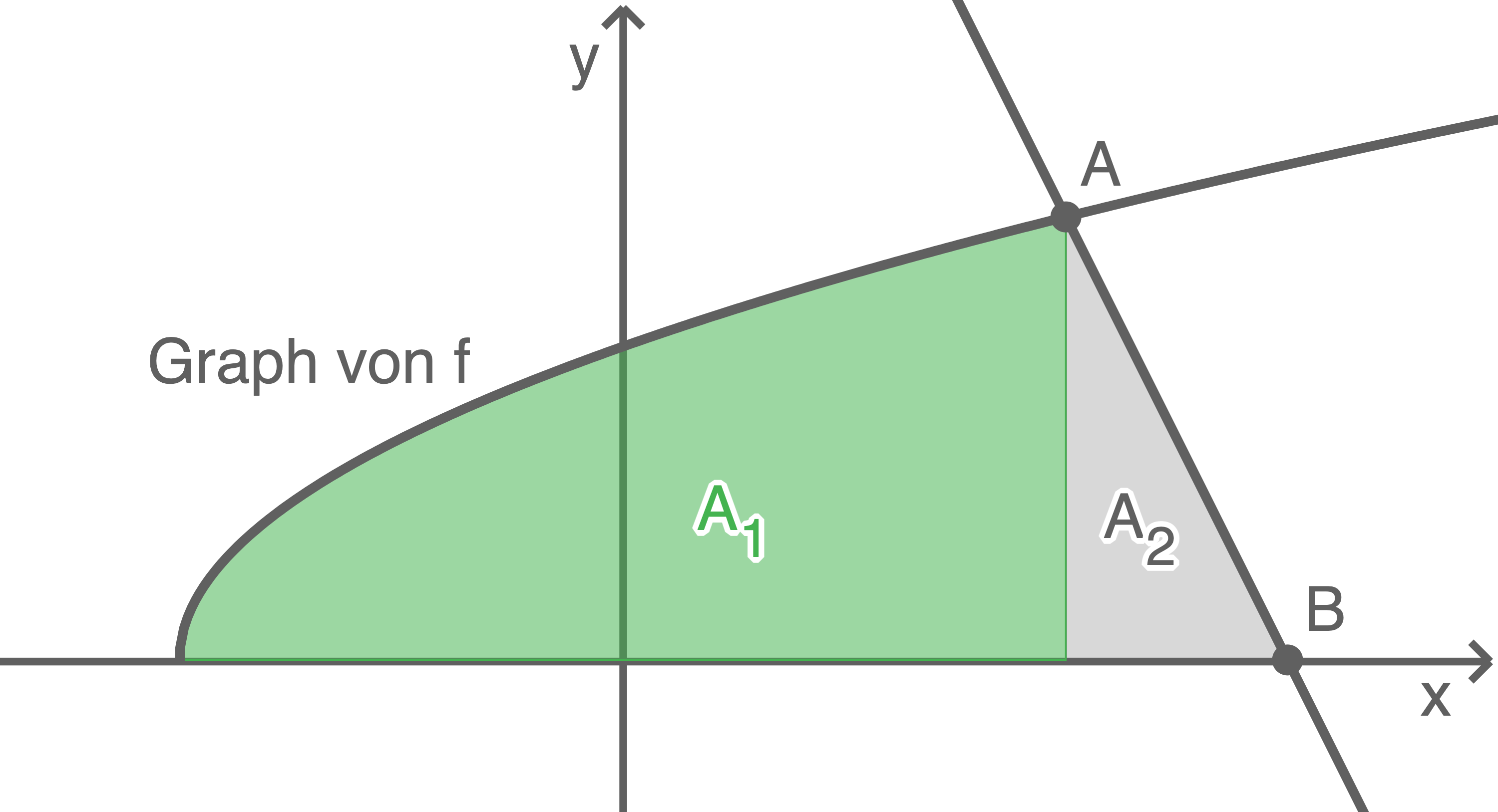
Die markierte Fläche kann in zwei Abschnitte unterteilt werden:
 Nullstelle von
Nullstelle von  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
f(x)&=& 0&\\[5pt]
\sqrt{x+2}&=& 0&\quad \scriptsize \mid\; (\;)^2\\[5pt]
x+2&=& 0&\quad \scriptsize \mid\; -2\\[5pt]
x&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/dc96107149a87d86f16b21a7a99f1a1a8372f9880447d1fd7b28e4ef79518ec8_light.svg) Für den Inhalt der Fläche
Für den Inhalt der Fläche  folgt:
folgt:
![\(\begin{array}[t]{rll}
A_1&=& \displaystyle\int_{-2}^{2}\sqrt{x+2}\;\mathrm dx&\\[5pt]
&=& \left[\dfrac{2}{3}\cdot (x+2)^{\frac{3}{2}}\right]_{-2}^2&\\[5pt]
&=& \dfrac{2}{3}\cdot (2+2)^{\frac{3}{2}}-\dfrac{2}{3}\cdot (-2+2)^{\frac{3}{2}}&\\[5pt]
&=& \dfrac{2}{3}\cdot 4^{\frac{3}{2}}-0&\\[5pt]
&=& \dfrac{2}{3}\cdot \sqrt{4^3}&\\[5pt]
&=& \dfrac{16}{3} \; [\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/6a121e99df0df1ddfd82f0a15b97b1f2a0b5a90b0fb5301d9e96ddf249b268c2_light.svg) Die Fläche
Die Fläche  entspricht einer Dreiecksfläche:
entspricht einer Dreiecksfläche:
![\(\begin{array}[t]{rll}
A_2&=& \dfrac{1}{2}\cdot a\cdot b & \\[5pt]
&=& \dfrac{1}{2}\cdot 1\cdot 2 & \\[5pt]
&=& 1 \; [\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/45801e24d6023de59a72c36c83d077ec8b835f9f4c8ce0fc44017908e607c40e_light.svg) Der Inhalt der markierten Fläche ist somit gegeben durch:
Der Inhalt der markierten Fläche ist somit gegeben durch:
![\(\begin{array}[t]{rll}
A&=& A_1+A_2& \\[5pt]
&=& \dfrac{16}{3}+1& \\[5pt]
&\approx& \dfrac{19}{3} \; [\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/5702a3c626c63999e42fd3f863960402d7be494d5e33439e40cb022d3a0b3c0f_light.svg)

Lösung 2
a)
Der Graph von  ergibt sich aus dem Graphen von
ergibt sich aus dem Graphen von  durch Verschiebung um 3 Längeneinheiten in positive
durch Verschiebung um 3 Längeneinheiten in positive  -Richtung und Spiegelung an der
-Richtung und Spiegelung an der  -Achse.
Aufgrund der Spiegelung entspricht der Hochpunkt des Graphen von
-Achse.
Aufgrund der Spiegelung entspricht der Hochpunkt des Graphen von  nach entsprechender Verschiebung also dem Tiefpunkt des Graphen von
nach entsprechender Verschiebung also dem Tiefpunkt des Graphen von  Durch Spiegelung an der
Durch Spiegelung an der  -Achse ergeben sich die Koordinaten des Tiefpunkts des Graphen von
-Achse ergeben sich die Koordinaten des Tiefpunkts des Graphen von  mit
mit 
b)
Lösung 3
a)
Der Abbildung kann entnommen werden, dass die Steigung des Graphen für  im Punkt
im Punkt  am größten ist.
Durch Einzeichnen der Tangente an den Graphen in diesem Punkt ergibt sich, dass die Steigung in diesem Punkt kleiner als 3 ist.
Die Aussage ist somit richtig.
am größten ist.
Durch Einzeichnen der Tangente an den Graphen in diesem Punkt ergibt sich, dass die Steigung in diesem Punkt kleiner als 3 ist.
Die Aussage ist somit richtig.
b)
Der Term  beschreibt das Volumen des Rotationskörpers der Fläche, die vom Graphen von
beschreibt das Volumen des Rotationskörpers der Fläche, die vom Graphen von  den Koordinatenachsen und der Gleichung
den Koordinatenachsen und der Gleichung  eingeschlossen wird.
eingeschlossen wird.
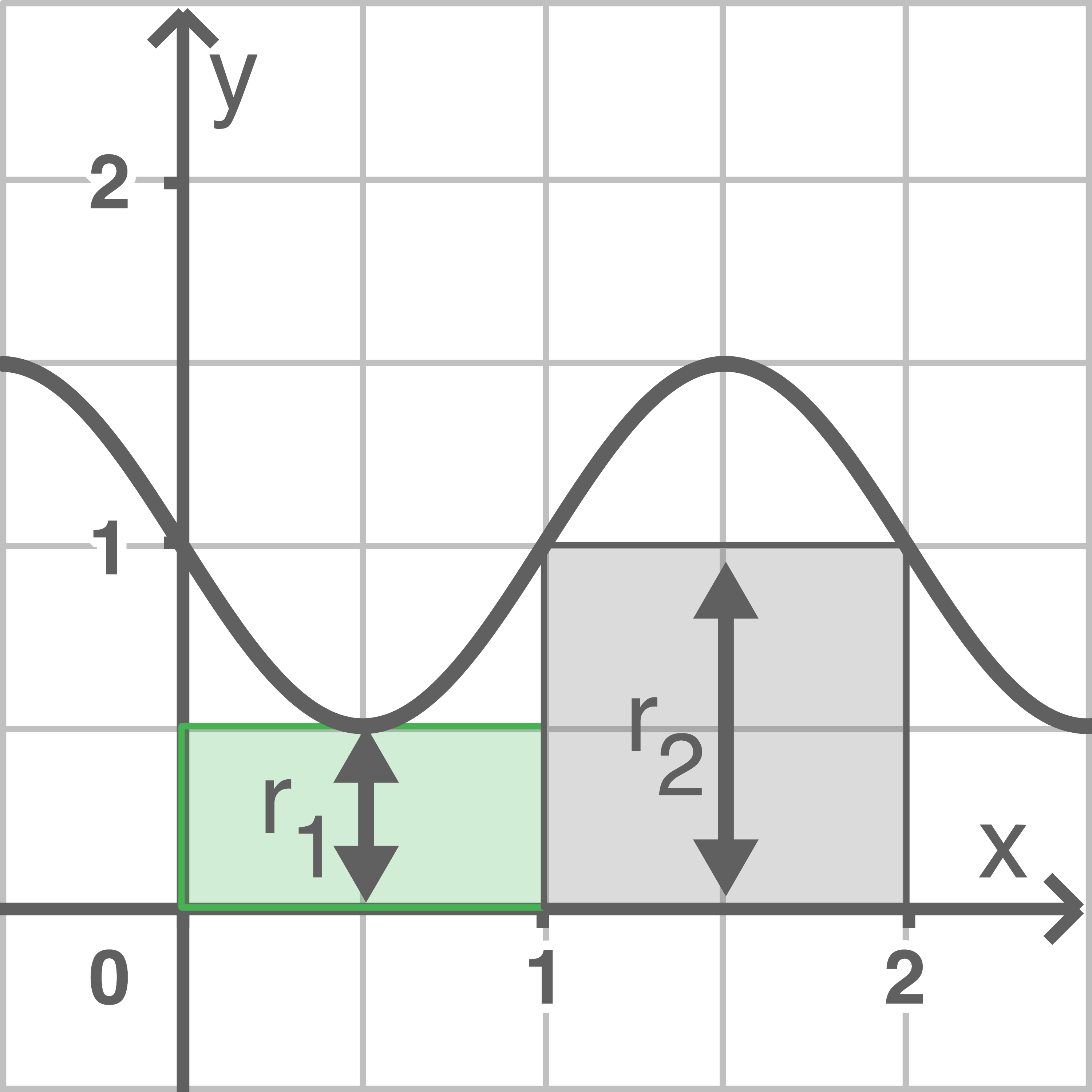
Der Term  beschreibt das Volumen der Rotationskörper zweier Zylinder mit den Radien
beschreibt das Volumen der Rotationskörper zweier Zylinder mit den Radien  und
und  und einer jeweiligen Höhe von 1.
Aus der Abbildung ergibt sich, dass das Volumen der rotierenden Zylinder folglich kleiner als das Volumen des rotierenden Graphen von
und einer jeweiligen Höhe von 1.
Aus der Abbildung ergibt sich, dass das Volumen der rotierenden Zylinder folglich kleiner als das Volumen des rotierenden Graphen von  ist.
ist.

Lösung 4
a)
Aus der Geradengleichung  lassen sich
lassen sich 
 und
und  herauslesen.
Einsetzen in die Ebenengleichung ergibt:
herauslesen.
Einsetzen in die Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
E: t+1+(1-t)&=& 2& \\[5pt]
2&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/41561129c9c5d9cdb32dfdd0794f4196cce8effdcc11282872ddacaa6a712c51_light.svg) Somit liegt die Gerade
Somit liegt die Gerade  in der Ebene
in der Ebene 
b)
Zwei Geraden sind genau dann windschief, wenn sie nicht parallel bzw. identisch parallel zueinander sind und keinen gemeinsamen Schnittpunkt haben.
Parallelität überprüfen:
Es muss gelten:
 Da aus der ersten Zeile
Da aus der ersten Zeile  , aus der zweiten Zeile
, aus der zweiten Zeile  und aus der dritten Zeile
und aus der dritten Zeile  folgt, hat diese Gleichung keine Lösung.
Die Gerade
folgt, hat diese Gleichung keine Lösung.
Die Gerade  und die Geraden der Schar
und die Geraden der Schar  sind folglich unabhängig von
sind folglich unabhängig von  weder parallel noch identisch parallel zueinander.
Schnittpunkt prüfen:
Aus der dritten Zeile folgt
weder parallel noch identisch parallel zueinander.
Schnittpunkt prüfen:
Aus der dritten Zeile folgt  und eingesetzt in die erste Zeile
und eingesetzt in die erste Zeile  Einsetzen in die zweite Zeile ergibt jedoch
Einsetzen in die zweite Zeile ergibt jedoch  was zu einem Widerspruch führt.
Die Gerade
was zu einem Widerspruch führt.
Die Gerade  und die Geraden der Schar
und die Geraden der Schar  haben somit keinen Schnittpunkt miteinander und sind folglich für jeden Wert von
haben somit keinen Schnittpunkt miteinander und sind folglich für jeden Wert von  windschief.
windschief.
Lösung 5
a)
b)
Da sich die Geraden  und
und  im Punkt
im Punkt  schneiden, muss dieser in der gesuchten Ebene liegen.
Die Gerade
schneiden, muss dieser in der gesuchten Ebene liegen.
Die Gerade  kann an den beiden Ebenen gespiegelt werden, welche sowohl den Punkt
kann an den beiden Ebenen gespiegelt werden, welche sowohl den Punkt  als auch die Gerade der Winkelhalbierenden der Richtungsvektoren von
als auch die Gerade der Winkelhalbierenden der Richtungsvektoren von  und
und  enthalten.
Da die beiden Richtungsvektoren der Geraden
enthalten.
Da die beiden Richtungsvektoren der Geraden  und
und  die gleiche Länge
die gleiche Länge  besitzen, ergeben sich die Normalenvektoren aus der Summe bzw. der Differenz der Richtungsvektoren.
Die Normalenvektoren
besitzen, ergeben sich die Normalenvektoren aus der Summe bzw. der Differenz der Richtungsvektoren.
Die Normalenvektoren  und
und  der beiden Spiegelebenen folgen also mit:
der beiden Spiegelebenen folgen also mit:

 Einsetzen des gemeinsamen Stützpunkts
Einsetzen des gemeinsamen Stützpunkts  in die allgemeine Ebenengleichung liefert:
Eine mögliche Ebenengleichung ergibt sich also mit:
in die allgemeine Ebenengleichung liefert:
Eine mögliche Ebenengleichung ergibt sich also mit:
![\(\begin{array}[t]{rll}
E_1: \quad 3\cdot x_1+3\cdot x_2&=& 6&\quad \scriptsize \mid\; :3\\[5pt]
x_1+x_2&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/9c5d5f57cfab7be5a298248b8a6ecc13e496f917205375a61c9326fde20aa6a5_light.svg) Analog gilt:
Eine mögliche Ebenengleichung ergibt sich also außerdem mit:
Analog gilt:
Eine mögliche Ebenengleichung ergibt sich also außerdem mit:

Lösung 6
a)
„Es werden zwei Kugeln aus dem Behälter gezogen, die mit unterschiedlichen Zahlen beschriftet sind."
b)