Wahlteil B2

Die Punkte $A(6\mid 6 \mid 0)$ , $B(2\mid 8 \mid 0)$ und $O(0\mid 0\mid 0)$ sind Eckpunkte einer dreiseitgen Pyramide mit der Spitze $S(4\mid 6 \mid 10)$ . Die Ebene $E$ enthält die Punkte $A,B$ und $C(2 \mid 3 \mid 5)$ .

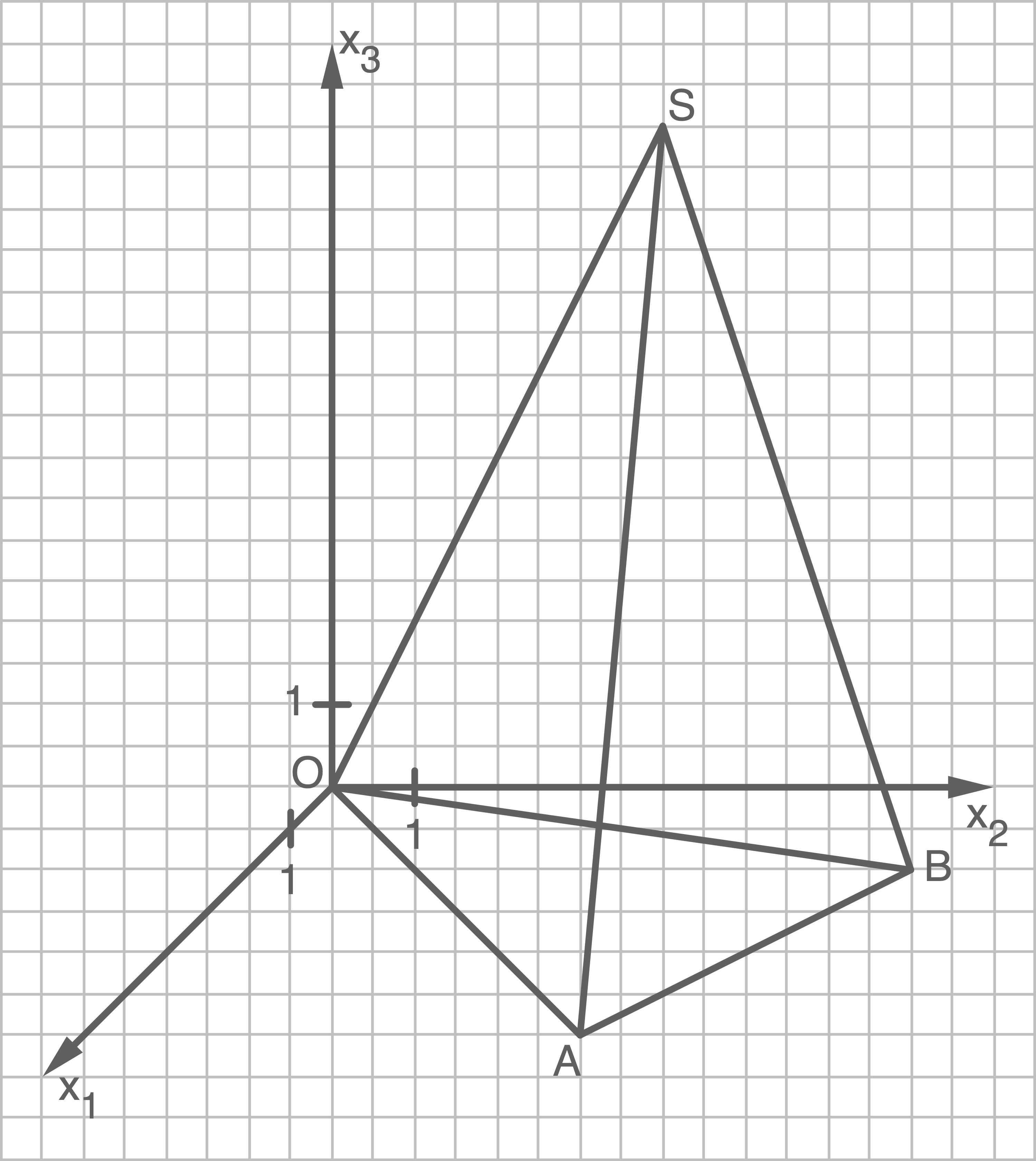
Stelle die Pyramide in einem geeigneten Koordinatensystem dar.
Bestimme eine Koordinatengleichung der Ebene $E$ .
(Teilergebnis: $E:x_1+2x_2+2x_3=18$ )

(3 VP)

Zeige, dass das Dreieck $ABC$ gleichschenklig ist.
Berechne das Volumen der Pyramide, die das Dreieck $ABC$ als Grundfläche und den Punkt $S$ als Spitze hat.

(4 VP)

In einem Koordinatensystem, bei dem die $x_1x_2$ -Ebene den Erdboden beschreibt, stellt die Pyramide $ABOS$ ein Kunstwerk dar (Koordinatenangaben in $\text {m}$ ).
An der Stelle, die durch den Punkt $F(8\mid 3 \mid 0)$ beschrieben wird, steht ein Mast senkrecht auf dem Erdboden. Auf dem Mast treffendes Sonnenlicht lässt sich durch parallele Geraden mit dem Richtungsvektor $\overrightarrow{v}= \pmatrix{-9\\1\\-4}$ beschreiben.
Der Schattenpunkt der Mastspitze liegt auf der Kante des Kunstwerks, die durch die Strecke $OS$ beschrieben wird.
Beschreibe ein Verfahren, mit dem man die Höhe des Masts rechnerisch bestimmen kann.

(3 VP)

Pyramide im Koordinatensystem darstellen

Diagramm eines dreidimensionalen Koordinatensystems mit Punkten und Linien.

Koordinatengleichung bestimmen

Ein Normalenvektor von $E$ wird mithilfe des Kreuzproduktes zweier Verbindungsvektoren der drei Punkte $A,$ $B$ und $C$ bestimmt:

$\begin{array}[t]{rll} \overrightarrow{n} &=& \overrightarrow{AB}\times \overrightarrow{AC} \\[5pt] &=& \pmatrix{-4\\2\\0}\times \pmatrix{-4\\-3\\5} \\[5pt] &=& \pmatrix{2\cdot 5 - 0\cdot (-3) \\ 0\cdot (-4) - (-4)\cdot 5 \\ (-4) \cdot (-3) - 2\cdot (-4) }\\[5pt] &=& \pmatrix{10\\20 \\ 20} \\[5pt] &=& 10\cdot \pmatrix{1\\2\\2} \end{array}$

Du kannst nun sowohl den ursprünglichen Normalenvektor als auch den gekürzten verwenden. Mithilfe einer Punktprobe mit einem der drei Punkte erhältst du:

$A(6\mid 6\mid 0)$ in $E:$

$\begin{array}[t]{rll} x_1 +2x_2 +2x_3 &=& d \\[5pt] 6 +2\cdot 6 + 2\cdot 0 &=& d \\[5pt] 18 &=& d \end{array}$

Eine Gleichung von $E$ in Koordinatenform lautet:

$E:x_1 +2x_2 +2x_3 = 18$

Gleichschenkligkeit zeigen

$\begin{array}[t]{rll} \left|\overrightarrow{AC} \right| &=& \left|\pmatrix{-4\\-3\\5} \right|\\[5pt] &=& \sqrt{(-4)^2 +(-3)^2 +5^2 } \\[5pt] &=& \sqrt{50} \\[10pt] \left|\overrightarrow{BC} \right| &=& \left|\pmatrix{0\\-5\\5} \right|\\[5pt] &=& \sqrt{0^2 +(-5)^2 +5^2 } \\[5pt] &=& \sqrt{50} \\[10pt] \end{array}$

Zwei Seiten des Dreiecks $ABC$ sind gleich lang. Das Dreieck ist also gleichschenklig.

Volumen der Pyramide berechnen

1. Schritt: Größe der Grundfläche berechnen

Da das Dreieck $ABC$ gleichschenklig ist und $\overline{AC}$ und $\overline{BC}$ die beiden Schenkel sind, ist $\overline{AB}$ die Grundseite.
Die zugehörige Höhe verläuft vom Mittelpunkt von $\overline{AB}$ zum Punkt $C.$

$\begin{array}[t]{rll} \overrightarrow{OM}_{AB} &=& \frac{1}{2} \cdot \left( \overrightarrow{OA} +\overrightarrow{OB}\right) \\[5pt] &=& \frac{1}{2} \cdot \left( \pmatrix{6\\6\\0} +\pmatrix{2\\8\\0}\right) \\[5pt] &=& \pmatrix{4\\7\\0} \\[10pt] h_{ABC} &=& \left|\overrightarrow{MC}\right| \\[5pt] &=& \left| \pmatrix{-2\\-4\\5} \right| \\[5pt] &=& \sqrt{(-2)^2 +(-4)^2 +5^2 } \\[5pt] &=& \sqrt{45} \\[10pt] \left|\overrightarrow{AB} \right| &=& \left|\pmatrix{-4\\ 2\\ 0} \right| \\[5pt] &=& \sqrt{(-4)^2 +2^2 +0^2 } \\[5pt] &=& \sqrt{20}\\[5pt] \end{array}$

Für den Flächeninhalt des Dreiecks $ABC$ folgt:

$\begin{array}[t]{rll} G &=& \frac{1}{2}\cdot \left|\overrightarrow{AB} \right|\cdot h_{ABC} \\[5pt] &=& \frac{1}{2} \cdot \sqrt{20} \sqrt{45} \\[5pt] &=& 15\\[5pt] \end{array}$

2. Schritt: Höhe der Pyramide berechnen

Die Höhe der Pyramide entspricht dem Abstand der Spitze $S$ zur Ebene $E.$ Verwende also die Hessesche Normalform von $E:$

$\begin{array}[t]{rll} x_1 + 2x_2 +2x_3 &=& 18 \quad \scriptsize \mid\; -18 \\[5pt] x_1 + 2x_2 +2x_3 -18 &=& 0 \\[5pt] \end{array}$

HNF bilden und $S$ einsetzen:

$\begin{array}[t]{rll} \dfrac{x_1 + 2x_2 +2x_3 -18}{\left|\pmatrix{1\\2\\2} \right|} &=& 0 \\[5pt] \dfrac{x_1 + 2x_2 +2x_3 -18}{\sqrt{1^2+2^2+2^2}} &=& 0 \\[5pt] \dfrac{x_1 + 2x_2 +2x_3 -18}{3} &=& 0 \\[5pt] \end{array}$

$d(E,P) = \dfrac{\left| x_1 + 2x_2 +2x_3 -18 \right|}{3}$

Einsetzen von $S$ ergibt:

$\begin{array}[t]{rll} h&=& d(E,S) \\[5pt] &=& \dfrac{\left| 4 + 2\cdot 6 +2\cdot 10 -18 \right|}{3} \\[5pt] &=& 6 \\[5pt] \end{array}$

3. Schritt: Volumen berechnen

$\begin{array}[t]{rll} V &=& \dfrac{1}{3}\cdot G\cdot h \\[5pt] &=& \dfrac{1}{3} \cdot 15\cdot 6\\[5pt] &=& 30 \\[5pt] \end{array}$

Das Volumen der Pyramide mit der Grundfläche $ABC$ und der Spitze $S$ beträgt $30\,\text{VE}.$

Verfahren beschreiben

Der Mast liegt im Modell auf der Geraden $m: \overrightarrow{x} = \overrightarrow{OF} + r\cdot \pmatrix{0\\0\\1}.$
Der Schatten des Mastes liegt demnach in der Ebene
$K:\, \overrightarrow{x}=$ $\overrightarrow{OF} + r\cdot \pmatrix{0\\0\\1} + s\cdot \overrightarrow{v}.$

Die Kante des Kunstwerks, die durch die Strecke $OS$ beschrieben wird, liegt auf der Geraden $OS:\ \overrightarrow{x} = t\cdot \overrightarrow{OS}.$

Bestimme den Schnittpunkt $M^*$ der Ebene $K$ mit der Geraden $OS.$ Dabei handelt es sich um den Schattenpunkt der Mastspitze.

Der Schattenpunkt $M^*$ und die Mastspitze $M$ liegen auf einer gemeinsamen Geraden mit dem Richtungsvektor $\overrightarrow{v}:$
$g:\, \overrightarrow{x} = \overrightarrow{OM^*} + u\cdot \overrightarrow{v}$

Die Mastspitze $M$ liegt sowohl auf dieser Geraden $g,$ wie auch auf der Mastgeraden $m.$ Bestimme also den Schnittpunkt dieser beiden Geraden.

Die $x_3$ -Koordinate von $M$ beschreibt dann die Höhe des Mastes in $\text{m}.$