Wahlteil C2
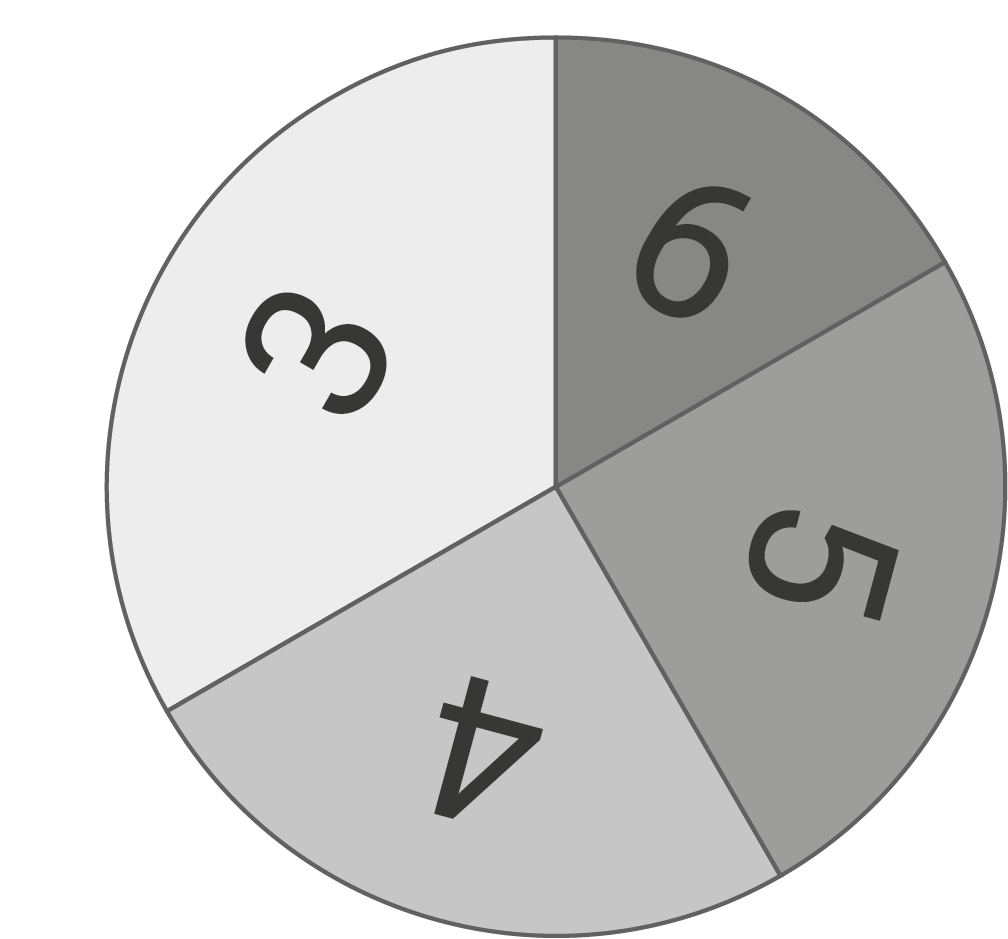
Beim einmaligen Drehen des abgebildeten Glücksrads erhält man eine von vier möglichen Punktzahlen.
Die Tabelle gibt für jede Punktzahl die zugehörige Wahrscheinlichkeit an.
Die Tabelle gibt für jede Punktzahl die zugehörige Wahrscheinlichkeit an.
| Punktzahl | Wahrscheinlichkeit |
| 3 | |
| 4 | |
| 5 | |
| 6 |
a)
Zehn Personen drehen das Glücksrad jeweils einmal. Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:
A: „Genau zwei Personen erzielen jeweils die Punktzahl 4.“
(0,5 VP)
B: „Mindestens drei Personen erzielen jeweils eine Punktzahl, die kleiner als 5 ist.“
(1,5 VP)
C: „Die Summe der erzielten Punktzahlen aller zehn Personen ist höchstens 31.“
(2 VP)
b)
Mehrere Spieler verwenden das Glücksrad bei einem Spiel mit folgenden Regeln:
. Bestimme die Mindestzahl der Spieler.
- Jeder Spieler dreht das Glücksrad einmal.
- Der Spieler mit der größten erzielten Punktzahl gewinnt.
- Erzielen mehrere Spieler diese größte Punktzahl, so gewinnt derjenige von ihnen, der als letzter gedreht hat.
(1 VP)
Die Wahrscheinlichkeit, dass Achim das Spiel gewinnt, ist kleiner als
(2 VP)
c)
Ein Spieler vermutet, dass die Wahrscheinlichkeit für die Punktzahl 3 bei dem vorliegenden Glücksrad nicht 
ist. Daher soll ein einseitiger Hypothesentest mit einer Stichprobe von 100 Drehungen auf einem Signifikanzniveau von 
durchgeführt werden. Dabei soll möglichst vermieden werden, dass irrtümlich von einer zu hohen Wahrscheinlichkeit für die Punktzahl 3 ausgegangen wird. Der Spieler entscheidet sich für folgende Nullhypothese:
„Die Wahrscheinlichkeit für die Punktzahl 3 beträgt höchstens .“
Beurteile, ob dieser Test der genannten Zielsetzung entspricht.
.
Bestimme die Wahrscheinlichkeit für den Fehler zweiter Art unter der Annahme, dass die Wahrscheinlichkeit für die Punktzahl 3 tatsächlich
beträgt.
(1 VP)
Formuliere den Fehler zweiter Art im Sachzusammenhang.
(1 VP)
Beim durchgeführten Test ergibt sich der Ablehnungsbereich Bestimme die Wahrscheinlichkeit für den Fehler zweiter Art unter der Annahme, dass die Wahrscheinlichkeit für die Punktzahl 3 tatsächlich
(1 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Ereignis A:
Anzahl der Personen mit Punktzahl 
ist binomialverteilt mit 
und 
Ereignis B:
Anzahl der Personen mit einer Punktzahl kleiner als 
ist binomialverteilt mit und 
Ereignis C:
Die Summe ist höchstens 
, wenn entweder alle zehn Personen die Punktzahl 
erzielen oder wenn neun Personen die Punktzahl erzielen und eine Person die Punktzahl 
b)
Spielverlauf beschreiben
Achim gewinnt, wenn jeder der folgenden Spieler die Punktzahl oder erzielt.
Mindestanzahl an Spielern bestimmen
Für die Anzahl 
der Mitspieler von Achim gilt:
Gesucht ist die kleinste natürliche Zahl , für die gilt: 
Aus 
und 
folgt, dass es mindestens 8 Mitspieler sind und somit mindestens 9 Spieler insgesamt sind.
c)
Hypothesentest beurteilen
Durch einen Hypothesentest kann die Wahrscheinlichkeit, die Nullhypotese fälschlicherweise abzulehnen, begrenzt werden, hier also die Wahrscheinlichkeit dafür, dass fälschlicherweise von einer zu hohen Wahrscheinlichkeit ausgegangen wird.
Der Test entspricht also der Zielsetzung.
Fehler zweiter Art im Sachzusammenhang formulieren
Obwohl die Wahrscheinlichkeit, die Punktzahl zu erhalten, mehr als beträgt, wird die Nullhypotese nicht abgelehnt.
Wahrscheinlichkeit des Fehlers zweiter Art bestimmen
Anzahl der Drehungen, bei denen man die Punktzahl erzielt.
ist binomialverteilt mit 
und 
