Wahlteil C1
Ein Onlineshop bietet Patronen mit schwarzer Tinte und Patronen mit farbiger Tinte an.
a)
Erfahrungsgemäß beträgt der Verkaufsanteil der Patronen mit schwarzer Tinte 
Betrachtet wird eine zufällige Auswahl von 100 verkauften Patronen. Es wird davon ausgegangen, dass dabei die Anzahl der Patronen mit schwarzer Tinte binomialverteilt ist. Bestimme die Wahrscheinlichkeiten folgender Ereignisse:
A: „Genau 66 der verkauften Patronen sind mit schwarzer Tinte gefüllt.“
vom Erwartungswert dieser Anzahl ab.“
(0,5 VP)
B: „Die Anzahl der verkauften Patronen mit schwarzer Tinte weicht um mehr als
(1,5 VP)
b)
Im Folgenden werden nur Patronen betrachtet, die mit schwarzer Tinte gefüllt sind. Die Füllmenge einer solchen Patrone wird als normalverteilt mit dem Erwartungswert 
und der Standardabweichung 
angenommen. Eine der beiden Abbildungen zeigt den Graphen der zugehörigen Dichtefunktion.
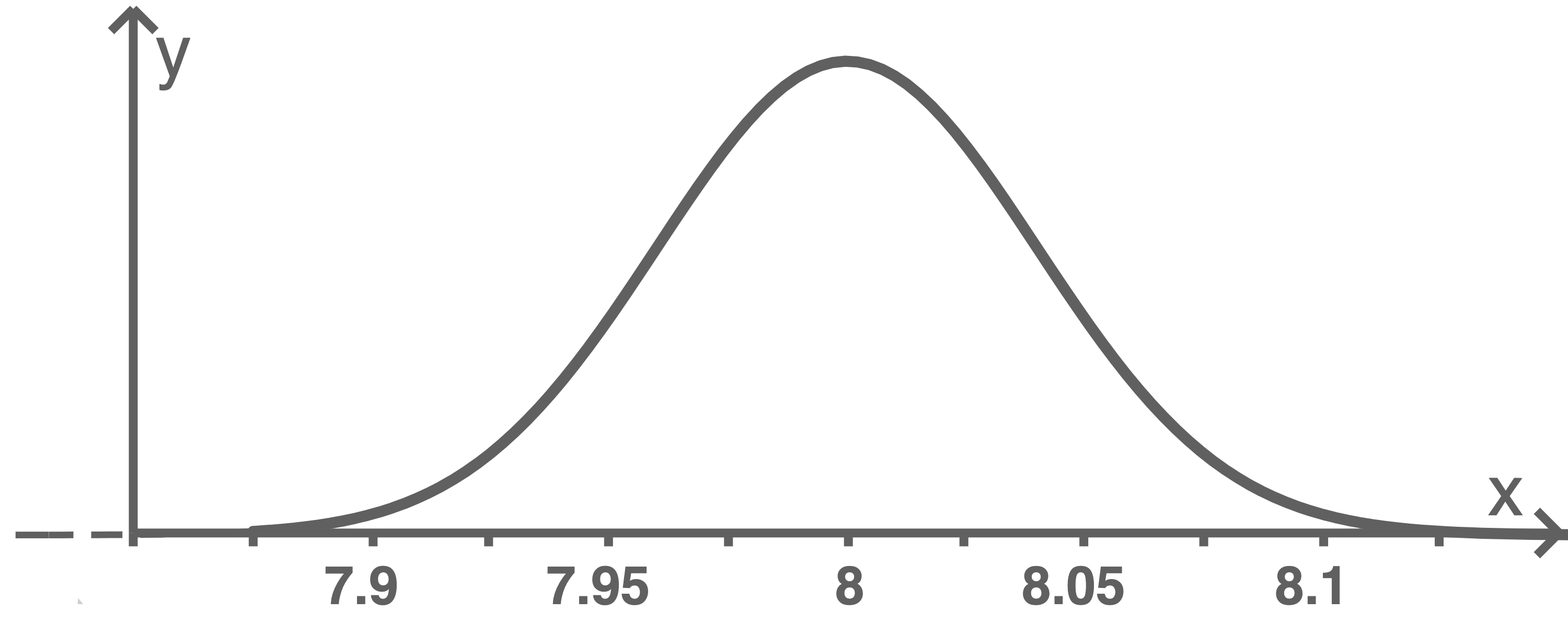
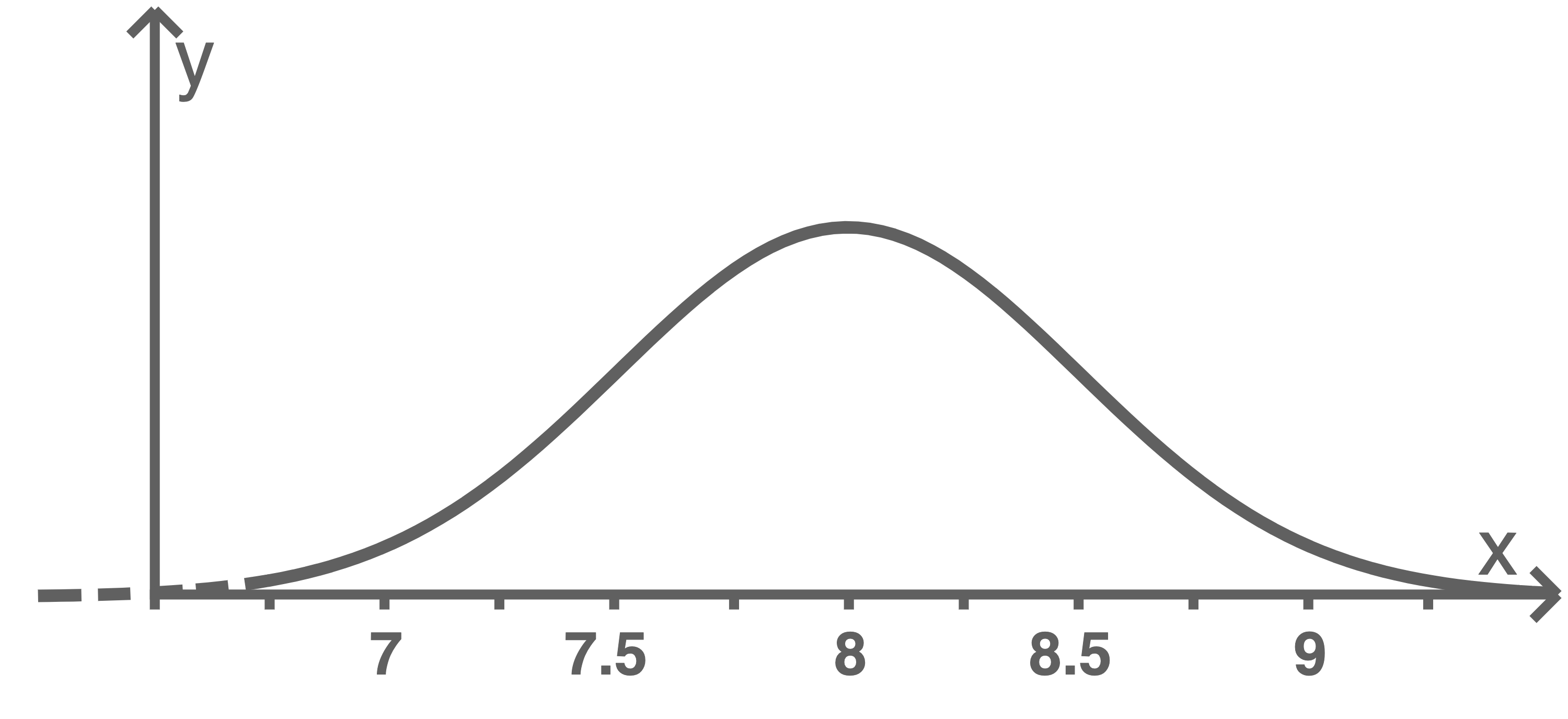Gib die Abbildung an, die den Graphen der zugehörigen Dichtefunktion nicht zeigt, und begründe deine Angabe.
Tinte enthält.
und 
Tinte enthält. Gib ein anderes Ereignis im Sachzusammenhang an, welches exakt dieselbe Wahrscheinlichkeit hat.
![\([a;b]\)](https://mathjax.schullv.de/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142?color=5a5a5a)
, so dass die Füllmenge einer zufällig ausgewählten Patrone mit einer Wahrscheinlichkeit von 
in liegt.
Abb. I
Abb. II
(1 VP)
Berechne die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Patrone weniger als
(0,5 VP)
Betrachtet wird das Ereignis, dass eine zufällig ausgewählte Patrone zwischen
(1 VP)
Bestimme das kleinste Intervall
(2 VP)
c)
Betrachtet wird die für 
definierte Funktion 
mit 
Weise nach, dass eine Dichtefunktion über ihrem Definitionsbereich ist.
beschrieben werden.
Mit einer Wahrscheinlichkeit von
wird eine Ware innerhalb von 
Stunden nach Eingang der Bestellung versandt. Bestimme den Wert von .
(2 VP)
Die Zeitdauer in Stunden zwischen dem Eingang einer Bestellung im Onlineshop und dem Versand der Ware kann modellhaft durch eine stetige Zufallsgröße mit Dichtefuntkion Mit einer Wahrscheinlichkeit von
(1,5 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
Falsche Abbildung angeben
Abbildung (II) zeigt nicht den Graphen der zugehörigen Dichtefunktion, da die Wendepunkte des Graphen nicht bei 
und 
liegen.
Wahrscheinlichkeit bestimmen
ist die Füllmenge der ausgewählten Patrone in 
.
ist normalverteilt mit 
und 
Ereignis formulieren
Da die Normalverteilung symmetrisch um ist, folgt:
E: „Eine zufällig ausgewählte Patrone enthält zwischen 
und 
Tinte.“
Intervall bestimmen
Das Intervall muss symmetrisch um den Erwartungswert liegen, da dort die Wahrscheinlichkeitsdichte am höchsten ist und das Intervall möglichst klein sein soll.
Aus 
ergibt sich:
und 
Es folgt also: 
und 
c)
Dichtefunktion nachweisen
zu zeigen:
für 
, da 
für alle 
Für 
folgt 
und somit 
Wert von bestimmen
Der Ansatz 
führt auf folgende Gleichung:
![\(\begin{array}[t]{rll}
-\mathrm e^{-0,25t}+1&=& 0,85 &\quad \scriptsize \mid\;-1 \\[5pt]
-\mathrm e^{-0,25t}&=& -0,15 &\quad \scriptsize \mid\;\cdot(-1) \\[5pt]
\mathrm e^{-0,25t}&=& 0,15 &\quad \scriptsize \mid\;\ln \\[5pt]
-0,25t&\approx& -1,897 &\quad \scriptsize \mid\;:(-0,25) \\[5pt]
t&\approx&7,59
\end{array}\)](https://mathjax.schullv.de/b4ea480ef35ca3cd925a0b6e4b55192db183c3164333920f4f47f9c271804fd1?color=5a5a5a)