Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=x^2 \cdot \mathrm e^{-5x}.$

(2 VP)

Aufgabe 2

Bestimme diejenige Stammfunktion $F$ der Funktion $f$ mit $f(x)=\sqrt{4x-7},$ für die $F(2)=1$ ist.

(1,5 VP)

Aufgabe 3

Löse die Gleichung $(x^2+8)\cdot( \mathrm e^{x-1}-1)=0.$

(1,5 VP)

Aufgabe 4

Der Graph der Funktion $f$ mit $f(x)=\dfrac{4}{x^2}$ schneidet die Gerade mit der Gleichung $y=4$ im Punkt $P\,(1\mid 4)$ und die Gerade mit der Gleichung $y=1$ im Punkt $Q\,(2 \mid 1)$ .
Berechne den Inhalt der markierten Fläche.

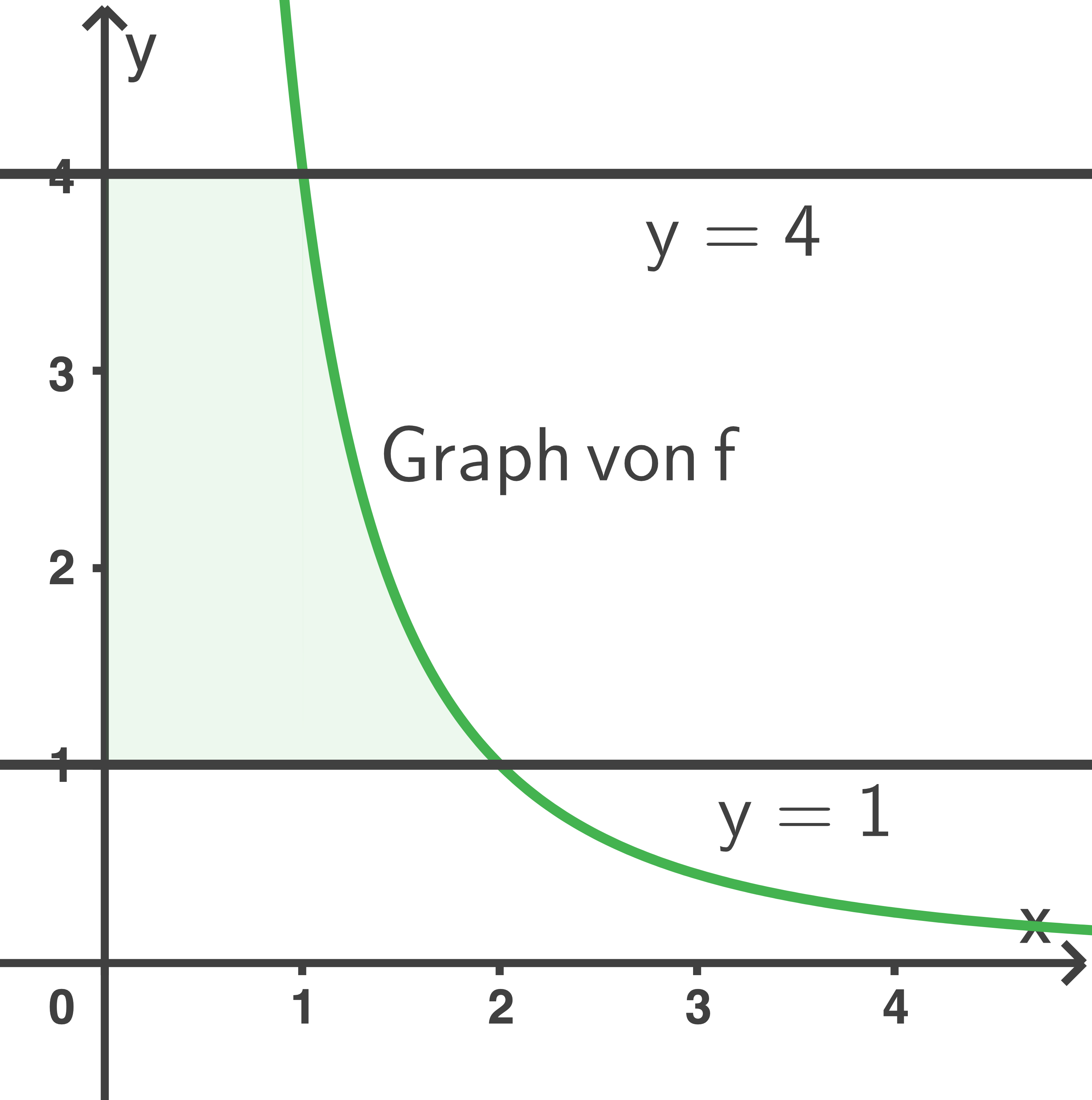
Graph einer Funktion mit y-Achse und horizontalen Linien bei y = 1 und y = 4.

(2,5 VP)

Aufgabe 5

Abgebildet ist der Graph einer Funktion $F$ .
$F$ ist die Stammfunktion einer ganzrationalen Funktion $f$ .

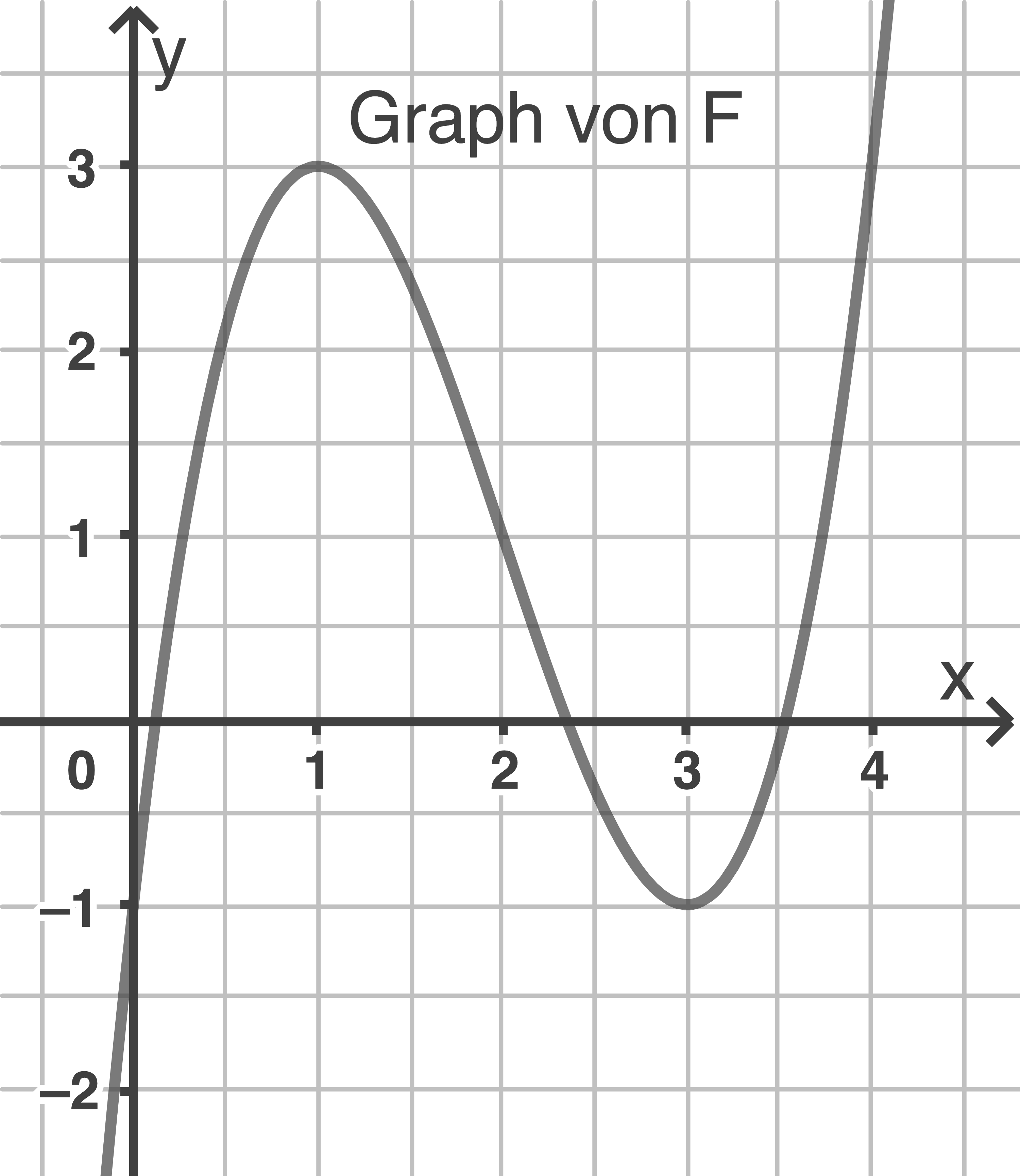
Graph von F in einem Koordinatensystem mit X- und Y-Achse.

Gib eine Nullstelle von $f$ im abgebildeten Bereich an.

Bestimme $\displaystyle\int_{1}^{2}f(x)\;\mathrm dx.$

Begründe, dass die Funktion $f$ im Bereich $0,5 \leq x \leq 1,5$ streng monoton fallend ist.

(2,5 VP)

Aufgabe 6

Gegeben sind die Ebenen:
$E$ : $2x_1+2x_2+x_3=6$ ; $F$ : $2x_2+x_3=4$ .

Stelle die beiden Ebenen in einem gemeinsamen Koordinatensystem dar.

Bestimme eine Gleichung der Schnittgeraden der beiden Ebenen.

Berechne den Abstand des Punktes $O\,(0 \mid 0 \mid 0)$ von der Ebene $E$ .

(5 VP)

Aufgabe 7

Eine Gerade ist orthogonal zur Ebene $E: \,x_1-x_3=5$ und schneidet die $x_1$ -Achse in einem Punkt, der vom Punkt $P\,(0 \mid 2 \mid 1)$ den Abstand $3$ hat.
Bestimme eine Gleichung einer solchen Geraden.

(2,5 VP)

Aufgabe 8

Auf einem Tisch liegen verdeckt vier rote und zwei schwarze Karten, mit denen Anna und Bernd das folgende Spiel spielen:
Anna deckt in der ersten Runde nacheinander zwei Karten auf und legt sie nebeneinander auf den Tisch. Ist darunter mindestens eine schwarze Karte, dann gewinnt Anna und das Spiel ist beendet. Andernfalls deckt Bernd nacheinander zwei der übrigen Karten auf. Deckt er dabei mindestens eine schwarze Karte auf, so gewinnt er, ansonsten gewinnt Anna.
Bestimme für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

Anna gewinnt das Spiel in der ersten Runde.

Anna gewinnt das Spiel.

(2,5 VP)

Lösung 1

Anwendung von Produkt- und Kettenregel:

$\(f$ $=\mathrm e^{-5x}(2x-5x^2)$

Lösung 2

$f(x)= \sqrt{4x-7} = (4x-7)^{\frac{1}{2}}$

$F(x)= \dfrac{1}{4} \cdot \dfrac{2}{3} \cdot (4x-7)^{\frac{3}{2}} +c$ $= \dfrac{1}{6} \cdot (4x-7)^{\frac{3}{2}} +c$

Mit $F(2)=1$ erhält man die gesuchte Stammfunktion:

$\begin{array}[t]{rll} F(2)&=&1\quad \scriptsize \\[5pt] \dfrac{1}{6} \cdot (4 \cdot 2-7)^{\frac{3}{2}} +c&=& 1&\quad \scriptsize \; \\[5pt] \dfrac{1}{6} +c&=& 1\quad \scriptsize \mid -\dfrac{1}{6}\; \\[5pt] c&=&\dfrac{5}{6} \end{array}$

$F(x)= \dfrac{1}{6} (4x-7)^{\frac{3}{2}} + \dfrac{5}{6}$ $=\dfrac{1}{6} \sqrt{(4x-7)^3} + \dfrac{5}{6}$

Lösung 3

Satz vom Nullprodukt: Ein Produkt ist genau dann Null, wenn einer der Faktoren Null ist.

$(x^2+8)$ ist immer größer Null, dehalb reicht es, den zweiten Faktor zu betrachten:

$\begin{array}[t]{rll} \mathrm e^{x-1}-1&=& 0\quad \scriptsize \mid \;+1 \\[5pt] \mathrm e^{x-1}&=& 1\quad \scriptsize \mid \;\ln()\; \\[5pt] x-1 &=& 0\quad \scriptsize \mid \;+1 \\[5pt] x&=&1 \end{array}$

$\mathbb{L}=\{1\}$

Lösung 4

Die Fläche wird in die zwei Teilflächen $A_1$ und $A_2$ unterteilt. $A_3$ dient als Hilfsfläche zur Berechnung von $A_2.$

$\begin{array}[t]{rll} A&=&A_1+A_2 \\[5pt] & =& 3 \cdot 1 + \displaystyle\int_{1}^{2}f(x)\;\mathrm dx -\underbrace{1 \cdot 1}_{A_3}\\[5pt] &=&3 + \left[-\dfrac{4}{x} \right]_1^2-1 \\[5pt] &=&3+\left(-\dfrac{4}{2}-\left(-\dfrac{4}{1}\right)\right)-1 \\[5pt] A&=&4\, \text{[FE]} \end{array}$

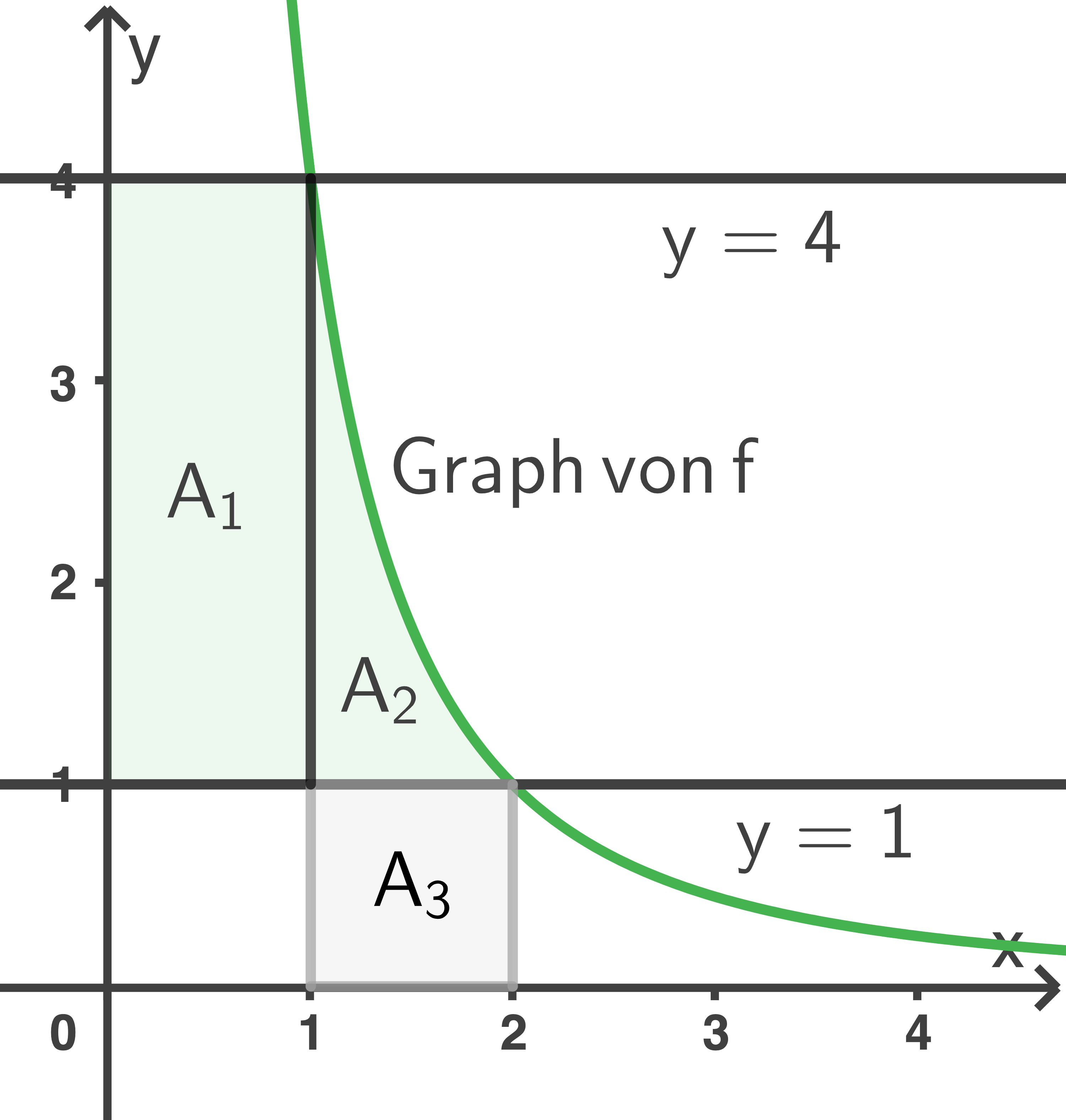
Graph einer Funktion mit den Bereichen A1, A2 und A3 sowie den Linien y = 4 und y = 1.

Lösung 5

$f$ ist die erste Ableitung von $F.$
Daher muss $f$ an den Extremstellen von $F$ Nullstellen besitzen.
Der Graph von $F$ hat Extremstellen bei $x_1=1$ und bei $x_2=3$ . An diesen Stellen besitzt $f$ also Nullstellen.

Das Integral wird berechnet, indem die Funktionswerte am Graphen von $F$ abgelesen werden.

$\displaystyle\int_{1}^{2}f(x)\;\mathrm dx = F(2)- F(1)$ $= 1- 3= -2$ .

Der Graph von $F$ ist im Bereich $0,5\leq x \leq 1,5$ rechtsgekrümmt, damit ist hier $\(F$ . Somit ist $f$ hier streng monoton fallend.

Lösung 6

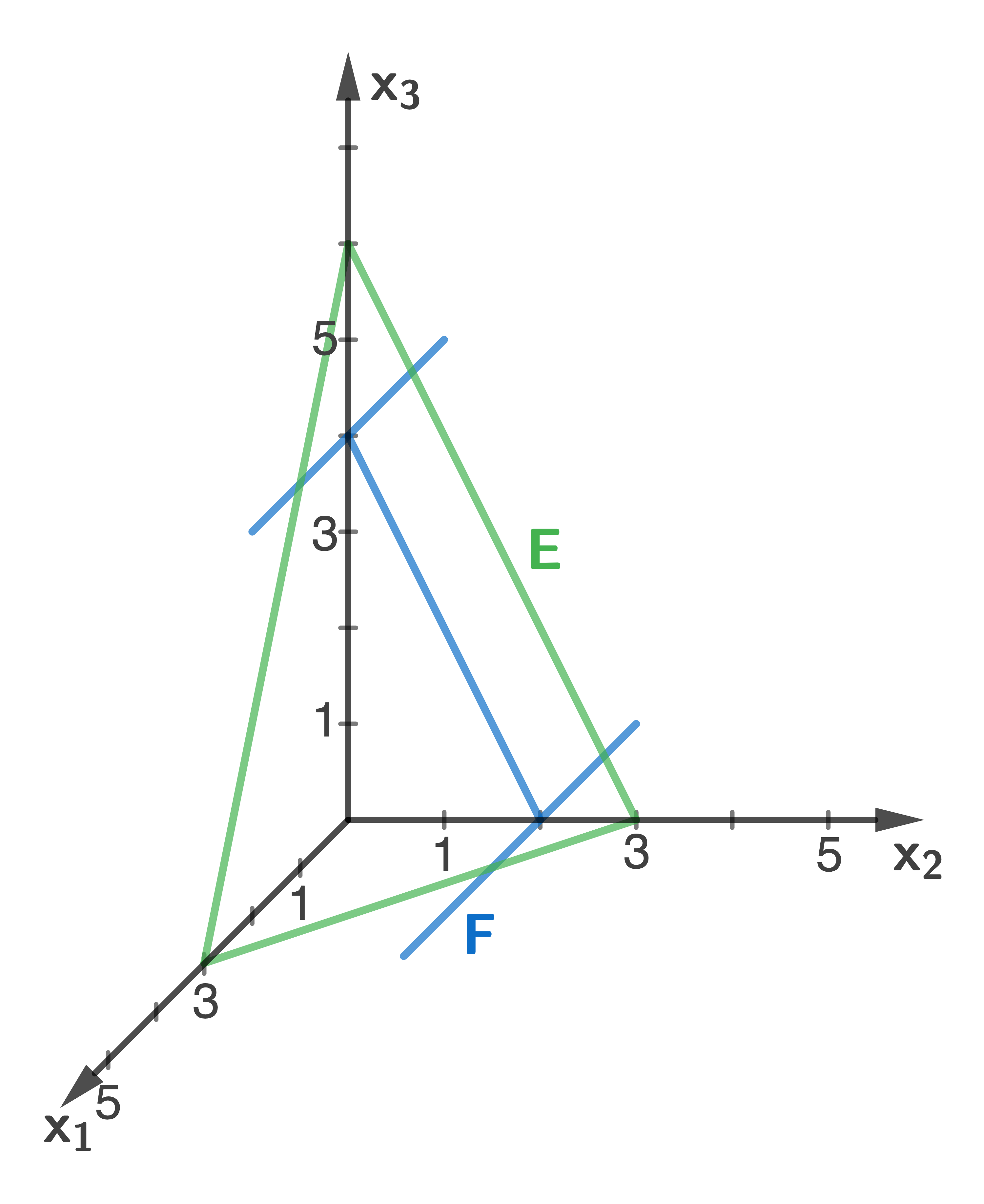
Dreidimensionales Koordinatensystem mit Linien und Dreiecken in verschiedenen Farben.

$x_2=t$ in $F$ eingesetzt ergibt $x_3=4-2t$ .

$x_1$ ergibt sich aus der Subtraktion von $F$ von $E$ : $2x_1=2,$ also $x_1=1$

$g: \overrightarrow{x}=\pmatrix{1\\t\\4-2t}$ $= \pmatrix{1\\0\\4} +t\cdot \pmatrix{0\\1\\-2}$

Lösungsweg A: Mit Hessescher Normalenform

1. Schritt: Normalenvektor der Ebene $E$ aufstellen

Ein Normalenvektor der Ebene $E$ wird aus der Koordinatenform abgelesen und ist $\overrightarrow{n}=\pmatrix{2\\2\\1}.$

2. Schritt: $\overrightarrow{n}$ und die Koordinaten von $O$ in die Formel der Hesseschen Normalenform einsetzen

$\begin{array}[t]{rll} d(O, E)&=& \left| \dfrac{2 \cdot 0 +2 \cdot 0 + 1\cdot 0 -6} {\sqrt{2^2+2^2+1^2}} \right| \\[5pt] &=& \left| \dfrac{-6}{\sqrt{9}} \right| \\[5pt] &=& \left| -2 \right| \\[5pt] &=& 2 \end{array}$

Der Abstand beträgt $2\,\text{LE}.$

Lösungsweg B: Mit Hilfsgerade

1. Schritt: Hilfsgerade $g$ aufstellen
Der Richtungsvektor der Hilfsgerade entspricht dem Normalenvektor der Ebene $E.$

$g:\overrightarrow{x}=\pmatrix{0\\0\\0}+s\pmatrix{2\\2\\1}$

2. Schritt: Koordinaten des Schnittpunkts $S$ von $g$ mit $E$ berechnen
$g$ in $E$ einsetzen:

$2(0+2s)+2(0+2s)+(0+s)=6,$ daraus folgt $9s=6,$ also $s=\frac{2}{3}.$

$S\left(\dfrac{4}{3}\mid\dfrac{4}{3}\mid\dfrac{2}{3}\right)$

3. Schritt: Abstand von $O$ zu $S$ berechnen

$d=\left|\pmatrix{\frac{4}{3}-0\\\frac{4}{3}-0\\\frac{2}{3}-0}\right|$ $=\sqrt{\left(\frac{4}{3}\right)^2+\left(\frac{4}{3}\right)^2+\left(\frac{2}{3}\right)^2}$ $=\sqrt{\frac{36}{9}}=\sqrt{4}=2$

Der Abstand beträgt $2\,\text{LE}.$

Lösung 7

Da die gesuchte Gerade orthogonal zur Ebene $E$ verläuft, stellt der Normalenvektor $\overrightarrow{n}=\pmatrix{1\\0\\-1}$ von $E$ den Richtungsvektor der Geraden dar.

Um die Geradengleichung vollständig aufzustellen, wird noch ein Stützvektor benötigt.
Der Schnittpunkt mit der $x$ -Achse liegt bei $S(a \mid 0 \mid 0)$ . Der Abstand von $S$ zum Punkt $P$ soll $3$ betragen.

Der Abstand zwischen den beiden Punkten wird wie folgt berechnet:

$\left| \overrightarrow{SP} \right | =\left| \pmatrix{0\\2\\1}-\pmatrix{a\\0\\0}\right |$ $= \sqrt{(0-a)^2+(2-0)^2+(1-0)^2}$

Dieser Abstand wird nun mit $3$ gleichgesetzt.

$\left| \overrightarrow{SP} \right | =3$

Vollständigen Rechenweg anzeigen

$a_{1/2}=\pm 2$

Damit kann zum Beispiel für $a=2$ folgende Geradengleichung aufgestellt werden:

$g: \overrightarrow{x}= \pmatrix{2\\0\\0} +t \cdot \pmatrix{1\\0\\-1}$ .

Lösung 8

Die Wahrscheinlichkeit dafür, eine rote Karte aufzudecken, liegt zu Beginn bei $\dfrac{4}{6}.$ Die Wahrscheinlichkeit, eine schwarze Karte aufzudecken, bei $\dfrac{2}{6}$ .

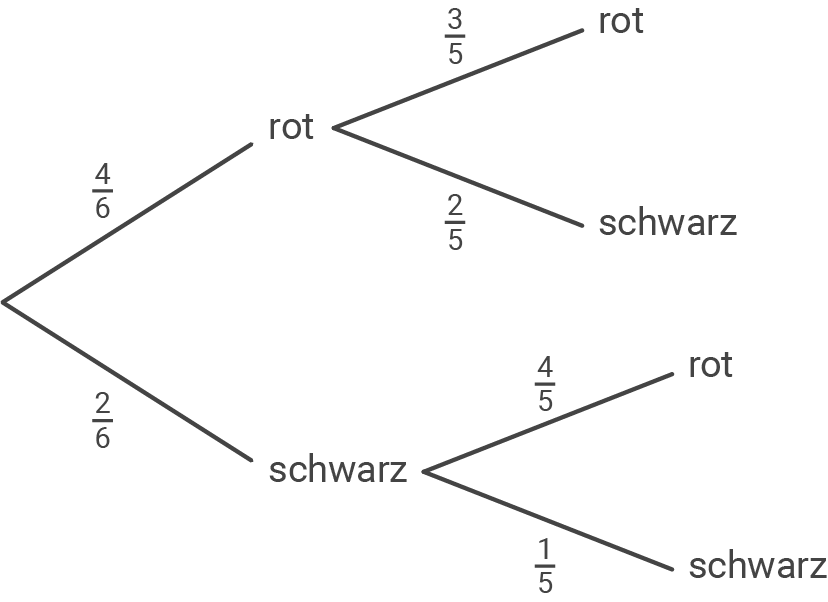Baumdiagramm mit zwei Farben, rot und schwarz, und dazugehörigen Brüchen.

Um zu gewinnen, muss Anna mindestens eine schwarze Karte aufdecken.

$P(A)= \dfrac{2}{6} \cdot \dfrac{1}{5} +\dfrac{2}{6} \cdot \dfrac{4}{5} + \dfrac{4}{6} \cdot \dfrac{2}{5} = \dfrac{3}{5}$

Damit Anna das Spiel gewinnt, darf Bernd keine schwarze Karte aufdecken. Dies passiert, wenn er nur rote Karten aufdeckt und Anna mindestens eine schwarze Karte aufdeckt.

$P(B)= P(A) + \dfrac{4}{6} \cdot \dfrac{3}{5} \cdot \dfrac{2}{4} \cdot \dfrac{1}{3} = \dfrac{2}{3}$