Pflichtaufgaben (P1-P4)
P1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  . Die Abbildung zeigt den Graphen
. Die Abbildung zeigt den Graphen  von
von  sowie die Tangenten an
sowie die Tangenten an  in den dargestellten Schnittpunkten mit der
in den dargestellten Schnittpunkten mit der  -Achse.
-Achse.
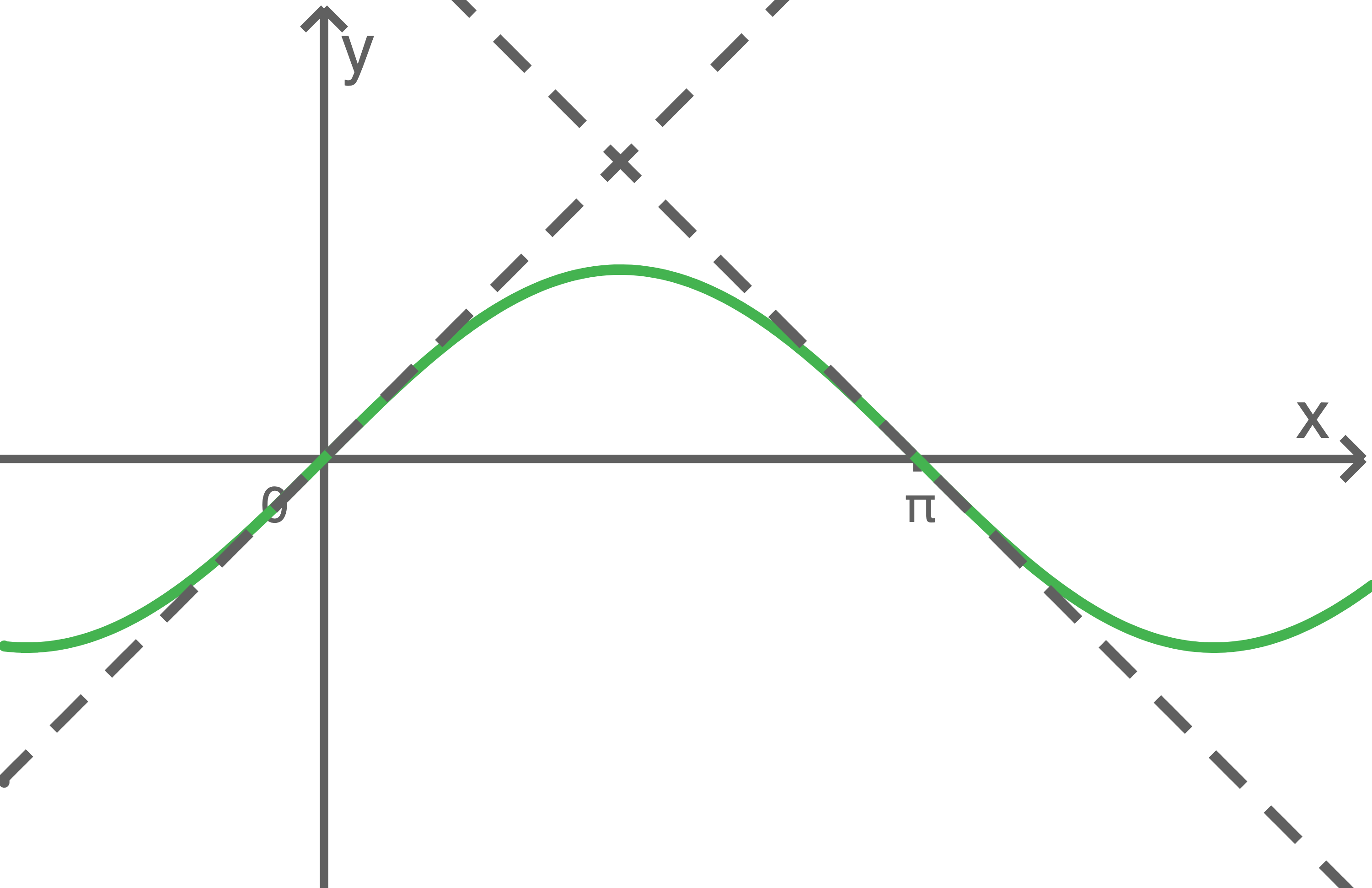
a)
Zeige, dass diejenige der beiden Tangenten, die durch den Koordinatenursprung verläuft, die Steigung  hat.
hat.
(1 BE)
b)
Berechne den Inhalt des Flächenstücks, das von  und den beiden Tangenten eingeschlossen wird.
und den beiden Tangenten eingeschlossen wird.
(4 BE)
P2
Gegeben ist eine in  definierte Funktion
definierte Funktion  mit
mit
 wobei
wobei  eine positive reelle Zahl ist.
eine positive reelle Zahl ist.
Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von
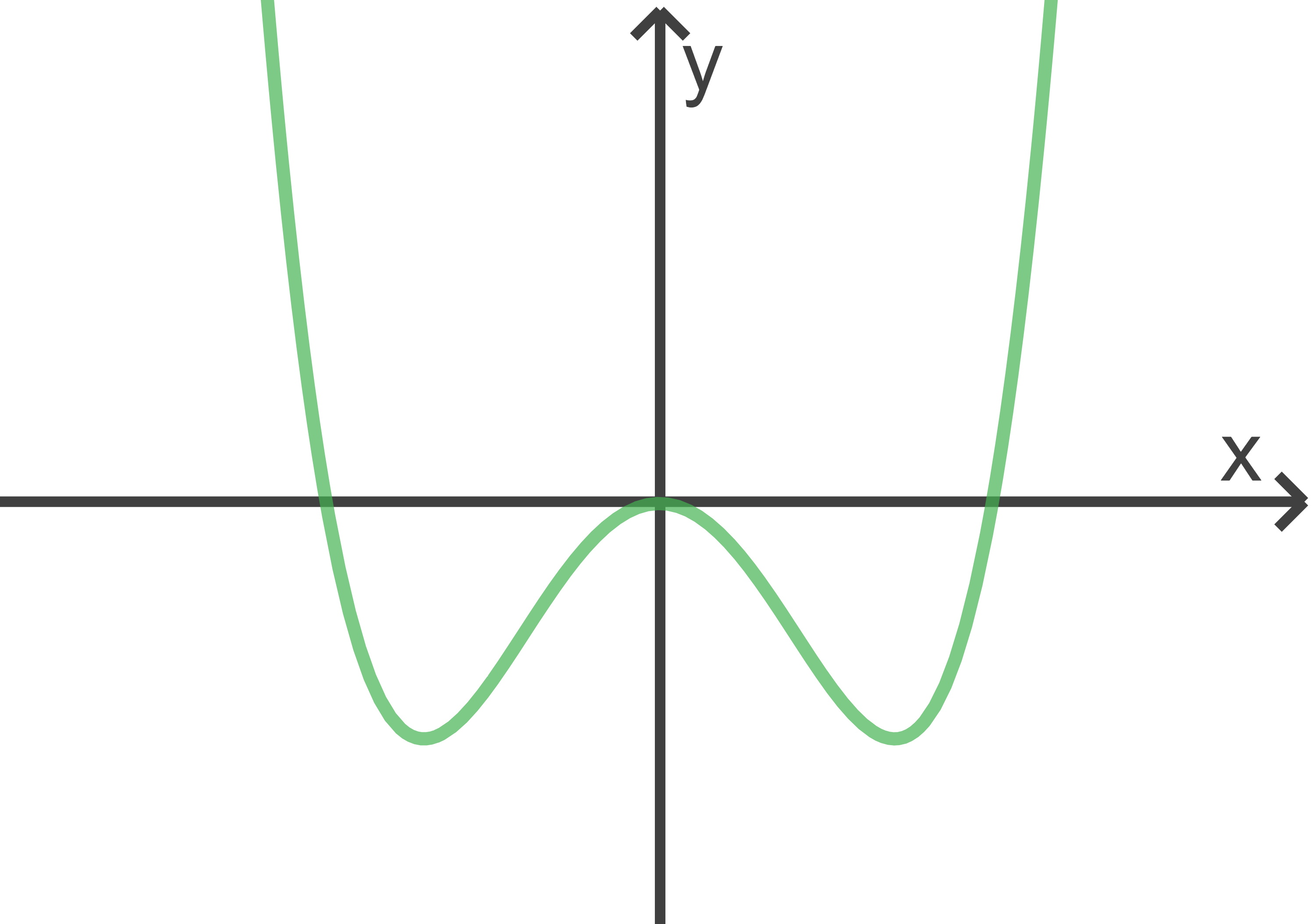
a)
Zeige, dass  eine Gleichung der ersten Ableitungsfunktion ist.
eine Gleichung der ersten Ableitungsfunktion ist.
(1 BE)
b)
Die beiden Tiefpunkte des Graphen von  haben jeweils die
haben jeweils die  Koordinate
Koordinate 
Ermittle den Wert von
Ermittle den Wert von
(4 BE)
P3
Betrachtet werden die Ebene  und für
und für  die Geraden
die Geraden
 mit
mit 
a)
Bestimme denjenigen Wert von  , für den die Gerade
, für den die Gerade  senkrecht zu
senkrecht zu  steht.
steht.
(2 BE)
b)
Untersuche, ob es einen Wert von  gibt, für den die Gerade
gibt, für den die Gerade  in
in  liegt.
liegt.
(3 BE)
P4
a)
In einem Gefäß befinden sich zwei rote und acht schwarze, sonst nicht unterscheidbare Kugeln.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit dafür, dass dabei genau eine rote Kugel gezogen wird.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit dafür, dass dabei genau eine rote Kugel gezogen wird.
(2 BE)
b)
In einem Gefäß befinden sich eine rote und  schwarze Kugeln.
schwarze Kugeln.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme den kleinsten Wert für für den gilt:
für den gilt:
Die Wahrscheinlichkeit dafür, dabei keine rote Kugel zu ziehen, beträgt mindestens 90 %.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme den kleinsten Wert für
Die Wahrscheinlichkeit dafür, dabei keine rote Kugel zu ziehen, beträgt mindestens 90 %.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
P1
a)
Der Graph von  schneidet die
schneidet die  -Achse unter anderem bei
-Achse unter anderem bei  . Es gilt also die Steigung von
. Es gilt also die Steigung von  an der Stelle
an der Stelle  zu berechnen. Mit
zu berechnen. Mit  folgt:
folgt:
 Damit hat die Tangente die Steigung
Damit hat die Tangente die Steigung 
b)
Um den Inhalt des Flächenstücks zu berechnen, wird die Symmetrie der Fläche bezüglich der zur  -Achse parallelen Gerade
-Achse parallelen Gerade  genutzt. Damit folgt:
genutzt. Damit folgt:
P2
a)
Durch Ableiten und Ausklammern ergibt sich:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/8f6f090a7ccbe003f602ff3ac56c324a8d006a5a076fc597160a773b13197d5b?color=5a5a5a)
b)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/95eedfe8abfba2896eb3feb44decef0e810bfda939a2c14229a2df491bc55766?color=5a5a5a) Nach dem Satz vom Nullprodukt muss entweder
Nach dem Satz vom Nullprodukt muss entweder  oder
oder  sein. Damit liegt die erste Extremstelle bei
sein. Damit liegt die erste Extremstelle bei  . Weiter ist:
. Weiter ist:
![\(\begin{array}[t]{rll}
2x^2-k &=&0 &\quad \scriptsize \mid\; +k \\[5pt]
2x^2 &=&k &\quad \scriptsize \mid\;:2 \\[5pt]
x^2 &=&\dfrac{k}{2} &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
x_{2/3} &=&\pm \sqrt{\dfrac{k}{2}}. &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/41964a3e5a4cbac7a2da2c41e69eb365c01ea1e6c60eae00b7bd046f430560c8?color=5a5a5a) Damit hat
Damit hat  zwei weitere Extremstellen bei
zwei weitere Extremstellen bei  und
und  .
Auf die hinreichende Bedingung kann verzichtet werden, da die Existenz zweier Tiefpunkte durch die Aufgabenstellung gegeben ist. Zwei Tiefpunkte können nicht aufeinander folgen, daher liegt bei
.
Auf die hinreichende Bedingung kann verzichtet werden, da die Existenz zweier Tiefpunkte durch die Aufgabenstellung gegeben ist. Zwei Tiefpunkte können nicht aufeinander folgen, daher liegt bei  ein Hochpunkt und bei
ein Hochpunkt und bei  und
und  jeweils ein Tiefpunkt.
2. Schritt: Berechnung des Wertes k
Für
jeweils ein Tiefpunkt.
2. Schritt: Berechnung des Wertes k
Für  und
und  gilt:
gilt:



 Für
Für  und
und  gilt ebenfalls:
gilt ebenfalls:
 Da die Tiefpunkte die
Da die Tiefpunkte die  -Koordinate
-Koordinate  haben, lässt sich
haben, lässt sich  durch folgende Gleichung ermitteln:
durch folgende Gleichung ermitteln:
![\(\begin{array}[t]{rll}
-\dfrac{k^2}{4}&=&-1 &\quad \scriptsize \mid\; \cdot(-4)\\[5pt]
k^2&=&4 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
k&=&2
\end{array}\)](https://mathjax.schullv.de/e8e761f6a223ebe33511f990a122daf948d12b4e1bfb25f8941087ffd1decc5f?color=5a5a5a) Für
Für  haben die beiden Tiefpunkte des Graphen von
haben die beiden Tiefpunkte des Graphen von  die
die  -Koordinate
-Koordinate 
P3
a)
b)
Damit  in der Ebene
in der Ebene  liegt, muss der Richtungsvektor von
liegt, muss der Richtungsvektor von  parallel zu
parallel zu  verlaufen und damit senkrecht zu
verlaufen und damit senkrecht zu  sein.
sein.
Skalarprodukt der beiden Vektoren bestimmen: Für sind die Gerade und die Ebene also parallel.
Liegt nun zusätzlich der Stützpunkt
sind die Gerade und die Ebene also parallel.
Liegt nun zusätzlich der Stützpunkt  von
von  auch in
auch in  dann liegt für
dann liegt für  ganz
ganz  in
in  Somit liegt die Gerade
Somit liegt die Gerade  für
für  in
in 
Skalarprodukt der beiden Vektoren bestimmen: Für
P4
a)
Anwenden der Pfadregeln:

 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird genau eine rote Kugel gezogen.
wird genau eine rote Kugel gezogen.
b)
Die Wahrscheinlichkeit keine rote Kugel zu ziehen, lässt sich durch folgenden Term darstellen:
 Damit folgt:
Der kleinste Wert für
Damit folgt:
Der kleinste Wert für  , bei dem die Aussage erfüllt wird, ist
, bei dem die Aussage erfüllt wird, ist 