Wahlteil C1

Auf einer Meeresfarm werden Muscheln zur Perlengewinnung gezüchtet.
Erfahrungsgemäß bringen $70\,\%$ der Muscheln keine Perlen hervor. In den restlichen Muscheln befindet sich jeweils genau eine Perle, aber nur $10\,\%$ der Perlen entsprechen dem geforderten Qualitätsstandard.

Bestimme für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
A: In $10$ zufällig ausgewählten Muscheln ist keine Perle.
B: In $10$ zufällig ausgewählten Muscheln sind insgesamt mindestens zwei Perlen.
C: In $100$ zufällig ausgewählten Muscheln sind insgesamt mehr als drei Perlen, die dem geforderten Qualitätsstandard entsprechen.

(3 VP)

Ermittle die Anzahl der Muscheln, die man mindestens öffnen muss, damit mit einer Wahrscheinlichkeit von mindestens $95\,\%$ mindestens eine Perle zu finden ist.

(2 VP)

Ein Muschelzüchter hat eine neue Zuchtmethode entwickelt. Er behauptet, damit die Wahrscheinlichkeit dafür, dass eine Muschel eine Perle hervorbringt, zu erhöhen. Um die Behauptung zu überprüfen, wird die Nullhypothese "Mit einer Wahrscheinlichkeit von höchstens $30\,\%$ bringt eine Muschel eine Perle hervor." getestet.
Man vereinbart einen Stichprobenumfang von $200$ Muscheln und ein Signifikanzniveau von $5\,\%$ .
Formuliere die zugehörige Entscheidungsregel.

(2,5 VP)

Ein Goldschmied hat in einer Schale weiße und schwarze Perlen. Es sind mehr schwarze als weiße Perlen. Insgesamt sind es $21$ Perlen. Der Goldschmied zieht zufällig zwei Perlen ohne Zurücklegen aus der Schale. Die Wahrscheinlichkeit dafür, dass sich die Farben der beiden Perlen unterscheiden, beträgt $\dfrac{8}{21}$ .
Bestimme die Anzahl der schwarzen Perlen, die vor dem Ziehen in der Schale waren.

(2,5 VP)

Die Wahrscheinlichkeit, dass keine Perle in der Muschel enthalten ist, beträgt 70%.
Die Wahrscheinlichkeit von A kann deshalb folgendermaßen berechnet werden:

$P(A)\approx 0,028$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit, dass eine Perle in der Muschel ist, beträgt 30 %.
$X_1$ ist die Anzahl der Muscheln, die Perlen enthalten.

$P(B) \approx 0,851$

Vollständige Lösung anzeigen

$X_2$ ist die Anzahl der Perlen, die dem Qualitätsstandard entsprechen. Die Wahrscheinlichkeit in einer Muschel eine Perle, die dem Qualitätsstandard entspricht, zu finden, ist: $0,3 \cdot 0,1 =0,03 =3$ %.

$P(C) \approx 0,353$

Vollständige Lösung anzeigen

$Y$ ist die Anzahl der Muscheln, die Perlen enthalten und ist binomialverteilt. Die Wahrscheinlichkeit eine Perle in einer Muschel zu finden beträgt 30 %, also ist $p=0,3$ .
Das n kennst du nicht. Gesucht ist das kleinste n mit $P(Y \geq 1)\geq 0,95$ , also $P(Y=0) \leq 0,05$ .
Es gilt $P(Y=0)= \pmatrix{n\\0 }\cdot 0,7^n \leq 0,05.$

$\begin{array}[t]{rll} 0,7^n&\leq &0,05 &\quad \scriptsize \mid \; \ln \\[5pt] \ln(0,7) \cdot n&\leq &\ln(0,05) &\quad \scriptsize \mid \; :\ln(0,7) \\[5pt] n&\geq& 8,4 \end{array}$

Es müssen mindestens neun Muscheln geöffnet werden.

Aus der Aufgabenstellung geht $n=200$ , $\alpha =0,05$ und $p_0=0,3$ hervor.
Z: Anzahl der Muscheln, die Perlen enthalten.
Stelle die Nullhypothese auf:

$H_0= p=p_0 \leq 0,3$

Trifft $H_0$ zu, so ist Z binomialverteilt mit $n$ und $p$ .

$H_1: p\gt p_0$

Gesucht wird die kleinste ganze Zahl, für die die Irrtumswahrscheinlichkeit bei $p=p_0$ höchstens $\alpha$ beträgt:

$P(Z\geq k) \leq 0,05$ bzw. $P(Z \leq k-1) \geq 0,95$ .

Die Wahrscheinlichkeiten aus der Binomialverteilungstabelle ergeben $P(Z\leq 70) \approx 0,946$ und $P(Z\leq 71) \approx 0,960$ .
Damit ergibt sich $k-1=71$ und $k=72$ .

Ist $Z\lt k$ , so wird die Nullhypothese nicht abgelehnt, für $Z\geq k$ wird sie abgelehnt. Bei einer Irrtumswahrscheinlichkeit von 5% kann man davon ausgehen, dass wenn mindestens 72 Muscheln Perlen enthalten, die Nullhypothese abgelehnt wird, ansonsten nicht abgelehnt wird.

Erstellen eines Baumdiagramms zur Übersicht:

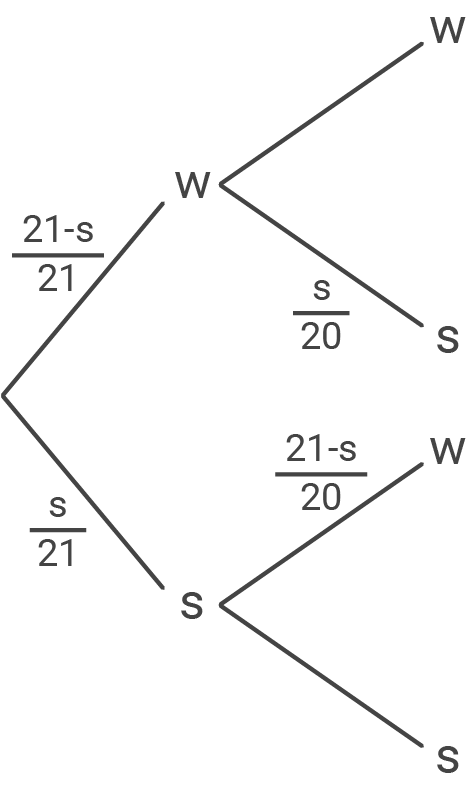Diagramm mit mathematischen Ausdrücken und Variablen für eine Analyse.

Mit $s$ (=Anzahl der schwarzen Perlen) muss gelten:

$\dfrac{s}{21} \cdot \dfrac{21-s}{20} +\dfrac{21-s}{21} \cdot \dfrac{s}{20}= \dfrac{8}{21}$

$\begin{array}[t]{rll} 21s -s^2+ 21s-s^2&=&160 &\quad \scriptsize \\[5pt] 2\cdot 21s -2 s^2&=&160 &\quad \scriptsize \mid\; : 2\\[5pt] -s^2 +21s&=&80 &\quad \scriptsize \mid +s^2 -2^1s\\[5pt] s^2-21s +80&=&0 \end{array}$

Mit der abc-Formel ergibt sich $s_1= 16$ und $s_2=5.$ Da die Anzahl der schwarzen Perlen größer sein soll, als die der weißen, waren vor dem Ziehen 16 schwarze Perlen in der Schale.