Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=\sqrt{x}\cdot\mathrm e^{2x}$ .

(2 VP)

Aufgabe 2

Berechne das Integral $\displaystyle\int\limits_{0}^{1}\dfrac{4}{(2x+1)^{3}}\mathrm dx$ .

(2 VP)

Aufgabe 3

Löse die Gleichung $x^{4}=4+3x^{2}$ .

(3 VP)

Aufgabe 4

Gegeben sind die Funktionen $f$ und $g$ mit $f(x)=\cos(x)$ und $g(x)=2\cos\left(\dfrac{\pi}{2}x\right)-2$ .

Beschreibe, wie man den Graphen von $g$ aus dem Graphen von $f$ erhält.

Bestimme die Nullstellen von $g$ für $0\leq x\leq 4$ .

(4 VP)

Aufgabe 5

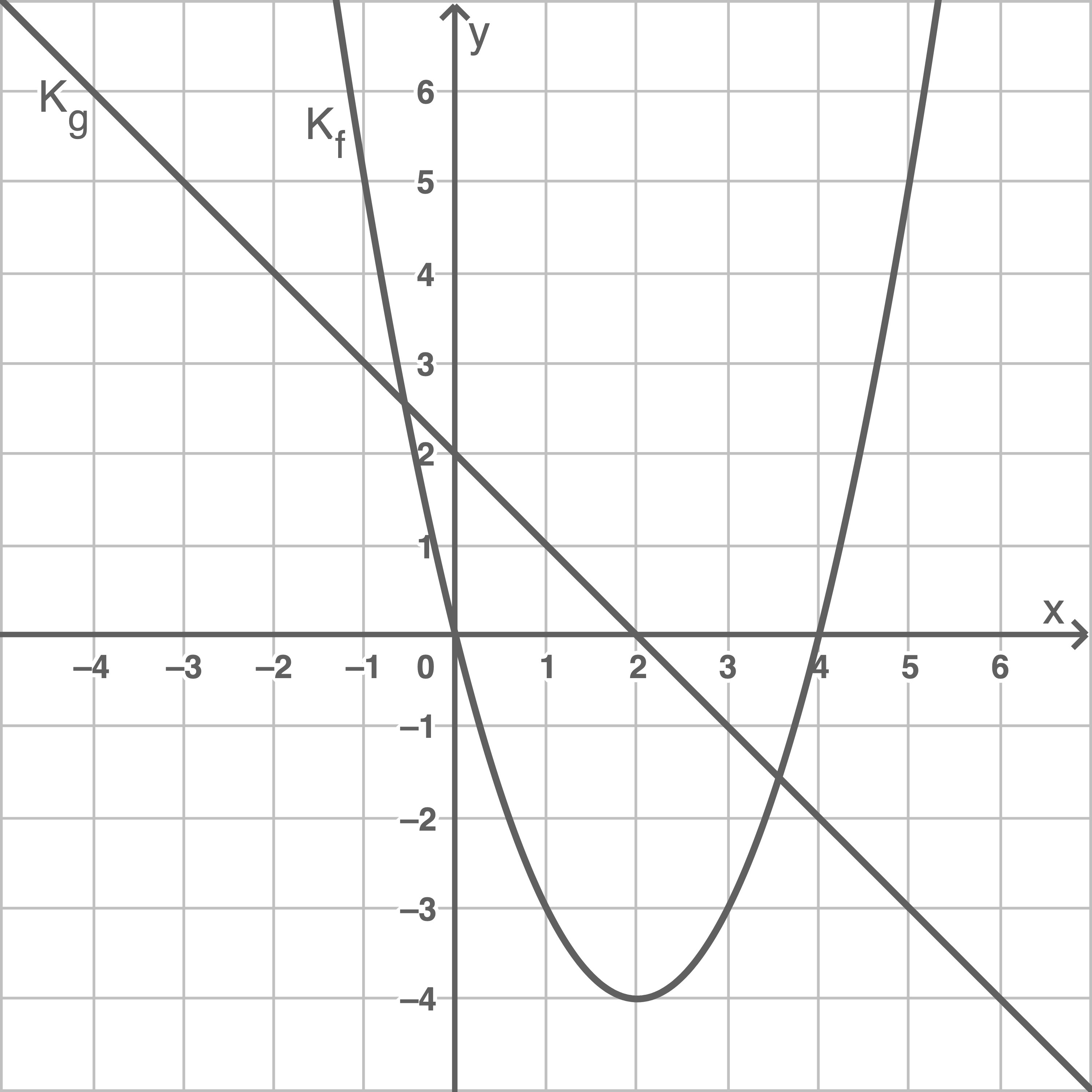
Diagramm mit einer Parabel und zwei Linien in einem Koordinatensystem. Achsen sind beschriftet.

Die Abbildung zeigt die Graphen $K_f$ und $K_g$ zweier Funktionen $f$ und $g$ .

Bestimme $f(g(3))$ .

Bestimme einen Wert für $x$ so, dass $f(g(x))=0$ ist.

Die Funktion $h$ ist gegeben durch $h(x)=f(x)\cdot g(x)$ .

Bestimme $\(h$ .

(4 VP)

Aufgabe 6

Gegeben sind die Ebenen $E:x_{1}+x_{2}=4$ und $F:x_{1}+x_{2}+2x_{3}=4$ .

Stelle die beiden Ebenen in einem gemeinsamen Koordinatensystem dar.

Gib eine Gleichung der Schnittgeraden von $E$ und $F$ an.

Die Ebene $G$ ist parallel zur $x_{1}$ -Achse und schneidet die $x_{2}x_{3}$ -Ebene in derselben Spurgeraden wie die Ebene $F$ .

Gib eine Gleichung der Ebene $G$ an.

(5 VP)

Aufgabe 7

Gegeben sind die Punkte $A(1\mid10\mid1)$ , $B(-3\mid13\mid1)$ und $C(2\mid3\mid1)$ .
Die Gerade $g$ verläuft durch $A$ und $B$ .

Bestimme den Abstand des Punktes $C$ von der Geraden $g$ .

(4 VP)

Aufgabe 8

An einem Spielautomaten verliert man durchschnittlich zwei Drittel aller Spiele.

Formuliere ein Ereignis $A$ , für das gilt:
$P(A)=\begin{pmatrix}10\\8\end{pmatrix}\cdot\left(\dfrac{2}{3}\right)^{8}\cdot\left(\dfrac{1}{3}\right)^{2}$ $+10\cdot\left(\dfrac{2}{3}\right)^{9}\cdot\dfrac{1}{3}+\left(\dfrac{2}{3}\right)^{10}$

Jemand spielt vier Spiele an dem Automaten.
Mit welcher Wahrscheinlichkeit verliert er dabei genau zwei Mal?

(3 VP)

Aufgabe 9

Gegeben sind der Mittelpunkt einer Kugel sowie eine Ebene.
Die Kugel berührt diese Ebene.

Beschreibe, wie man den Kugelradius und den Berührpunkt bestimmen kann.

(3 VP)

Lösung 1

$\blacktriangleright$ Bilde die Ableitung

Um die Ableitung zu bilden kannst du folgendermaßen vorgehen:

Schreibe den Wurzelterm der Funktion zunächst um
Leite die Funktion mit Hilfe der Produktregel und der Kettenregel ab

1. Schritt: Umschreiben

$\begin{array}{rll} f(x)&=&\sqrt{x}\cdot \mathrm e^{2x} \\[5pt] f(x)&=&x^{\frac{1}{2}}\cdot \mathrm e^{2x} \\[5pt] \end{array}$

2. Schritt: Ableiten

$\begin{array}{rll} f‘(x)&=&\dfrac{1}{2}x^{-\frac{1}{2}}\cdot \mathrm e^{2x}+x^{\frac{1}{2}}\cdot2\mathrm e^{2x}\\ f‘(x)&=&\left(\dfrac{1}{2\sqrt{x}}+2\sqrt{x}\right)\mathrm e^{2x}\\ \end{array}$

Lösung 2

$\blacktriangleright$ Berechne das Integral

Um das Integral zu berechnen, benötigst du eine Stammfunktion.
Es gilt der Hauptsatz der Integralrechnung:

$\begin{array}{rll} \displaystyle\int_{a}^{b}\mathrm f(x)dx&=&[F(x)]^{b}_a\\ &=&F(b)-F(a)\\ \end{array}$

Eine Stammfunktion einer Funktion $f$ bildest du folgendermaßen:

$\begin{array}{rll} f(x)&=&x^n\\[5pt] F(x)&=&\dfrac{1}{n+1}\cdot x^{n+1}+c\\[5pt] \end{array}$

Um die Stammfunktion der gegebenen Funktion zu bilden, kannst du diese zunächst als Produkt schreiben.

Rechenweg anzeigen

$\displaystyle\int_{0}^{1} \dfrac{4}{(2x+1)^3}\mathrm dx= \dfrac{8}{9}$

Lösung 3

$\blacktriangleright$ Löse die Gleichung

Um die Gleichung zu lösen, musst du zunächst alle Bestandteile der Gleichung auf eine Seite der Gleichung bringen. Der höchste Exponent von $x$ beträgt $4$ . Diese Gleichung kannst du demnach durch Substitution lösen. Anschließend kannst du die Gleichung entweder mit der Mitternachtsformel, oder der $\boldsymbol{pq}$ -Formel lösen. Anschließend musst du resubstituieren.

Rechenweg anzeigen

$u^2-3u-4=0$

Nun hast du eine quadratische Gleichung gegeben. Du kannst sie mit der Mitternachtsformel oder der $pq$ -Formel lösen.

Mitternachtsformel:

$\begin{array}{rll} x_{1,2}&=&\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\[5pt] \end{array}$

Es gilt: $a=1$ , $b=-3$ und $c=-4$

Setze diese Werte nun in die Mitternachtsformel ein.

$\begin{array}{rll} u_{1,2}&=&\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\[5pt] u_{1,2}&=&\dfrac{-(-3)\pm\sqrt{(-3)^2-4\cdot1\cdot(-4)}}{2\cdot1}\\[5pt] u_{1,2}&=&\dfrac{3\pm\sqrt{9+16}}{2}\\[5pt] u_{1,2}&=&\dfrac{3\pm\sqrt{25}}{2}\\[5pt] u_{1,2}&=&\dfrac{3\pm5}{2}\\[5pt] u_1&=&4\\[5pt] u_2&=&-1\\[5pt] \end{array}$

pq-Formel:

$\begin{array}{rll} x_1,2&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\ \end{array}$

Dabei gilt: $p=-3$ und $q=-4$

$\begin{array}{rll} u_{1,2}&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\[5pt] u_{1,2}&=&-\dfrac{-3}{2}\pm\sqrt{\left(\dfrac{-3}{2}\right)^2-(-4)}\\[5pt] u_{1,2}&=&\dfrac{3}{2}\pm\sqrt{\dfrac{9}{4}+4}\\[5pt] u_{1,2}&=&\dfrac{3}{2}\pm\sqrt{\dfrac{9}{4}+\dfrac{16}{4}}\\[5pt] u_{1,2}&=&\dfrac{3}{2}\pm\sqrt{\dfrac{25}{4}}\\[5pt] u_{1,2}&=&\dfrac{3}{2}\pm\dfrac{5}{2}\\[5pt] u_1&=&4\\[5pt] u_2&=&-1\\[5pt] \end{array}$

Nun kannst du resubstituieren. Dazu setzt du die Werte für $u_1$ und $u_2$ in die Gleichung $u=x^2$ ein.

$\begin{array}{rll} u_1&=&x^2\\ 4&=&x^2& \mid\; \scriptsize{\sqrt{\;}}\\ \pm\sqrt{4}&=&x_{1,2}\\ x_1&=&-2\\ x_2&=&2\\ \end{array}$

$\begin{array}{rll} u_2&=&x^2\\ -1&=&x^2& \mid\; \scriptsize{\sqrt{\;}}\\ \end{array}$

Da die Wurzel negativ ist, hat diese Gleichung keine Lösung.
Die Gleichung hat die Lösung $x_1=-2$ und $x_2=2$ . Die Lösungsmenge lautet also: $L=\{-2,2\}$

Lösung 4

a) $\blacktriangleright$ Erkläre den Graphen $\boldsymbol g$

Du hast in der Aufgabe zwei Kosinus-Funktionen gegeben.
Die allgemeine Kosinus-Funktion lautet:

$\begin{array}{rll} {f(x)}&=&{a\cdot\cos(bx+c)+d}\\ \end{array}$

Der Faktor $a$ gibt die Streckung bzw. Stauchung der Amplitude an. Durch den Faktor $b$ wird die Periode verändert. Eine Verschiebung in die $x$ -Richtung kommt durch den Faktor $c$ zustande. Das $d$ gibt eine Verschiebung in $y$ -Richtung an.
Um zu erklären wie man den Graphen $g$ aus $f$ erhält schaust du, wie sich die Amplitude und Periode ändert. Außerdem prüfst du, ob der Graph der Funktion $g$ verschoben ist.
Den Graphen $g$ erhältst du aus dem Graphen $f$ , indem die Funktion gestreckt und verschoben wird. Außerdem verändert sich die Periode.
Die Funktion $g$ hat demnach eine Amplitude von $2$ und ist um einen Faktor $2$ in negative $y$ -Richtung verschoben. Die Periode hat sich ebenfalls verändert. Die Periode wird mit folgender Formel berechnet:

$\begin{array}{rll} T&=&\dfrac{2\pi}{b}\\ \end{array}$

Die Funktion $g$ hat also die Periode $T=\dfrac{2\pi}{\frac{\pi}{2}}=4$ .

Du erhältst den Graphen $g$ aus dem Graphen $f$ , wenn du den Graphen $f$ mit $2$ streckst und um $2$ Längeneinheiten in negative $y$ -Richtung verschiebst. Außerdem ändert sich die Periode von $2\pi$ in $4$ .

b) $\blacktriangleright$ Bestimme die Nullstellen von $\boldsymbol g$

Bei dieser Teilaufgabe sollst du die Nullstellen der Funktion $g$ im Bereich $0\leq x\leq4$ bestimmen.
Setze dazu die Funktion $g$ gleich $0$ .

$\begin{array}{rll} 2\cos\left(\frac{\pi}{2}x\right)-2&=&0& \mid\; +2\\ 2\cos\left(\frac{\pi}{2}x\right)&=&2&\ \mid\; :2\\ \cos\left(\frac{\pi}{2}x\right)&=&1\\ \end{array}$

Die Kosinus-Funktion hat bei den Werten $0$ , $2\pi$ ,... den Wert $1$ .
Bestimme nun das $x$ so, dass der Kosinus diese Werte annimmt.

$\begin{array}{rll} \frac{\pi}{2}x&=&0& \mid\; \cdot\frac{2}{\pi}\\ x&=&0\\ \end{array}$

$\begin{array}{rll} \frac{\pi}{2}x&=&2\pi& \mid\; \cdot\frac{2}{\pi}\\ x&=&4\\ \end{array}$

Das bedeutet, dass die Funktion $g$ in dem gegebenen Bereich die Nullstellen $x_1=0$ und $x_2=4$ hat.

Lösung 5

a) $\blacktriangleright$ Bestimme $\boldsymbol{f(g(3))}$

Um $f(g(3))$ zu bestimmen, liest du zunächst den Wert von $g(3)$ ab. Anschließend liest du den Funktionswert von $f$ für diesen x-Wert ab.
Die Funktion $g$ hat an der Stelle $x=3$ den Wert $-1$ . Der Wert bei $f(-1)$ beträgt $5$
Der Wert $f(g(3))$ beträgt $5$ .

$\blacktriangleright$ Bestimme $\boldsymbol{f(g(x))=0}$

Bei dieser Aufgabe schaust du zunächst wo der Graph $K_f$ eine Nullstelle hat. Anschließend liest du den $x$ -Wert von $K_g$ ab, der diesen Wert hat.
Der Graph $K_f$ hat eine Nullstelle bei $x=4$ . Nun überprüfst du, wo der Graph $K_g$ den Wert $4$ annimmt. Dies ist bei $x=-2$ der Fall.

Alternativ
Der Graph $K_f$ hat bei $x=0$ eine Nullstelle. Der Graph $K_g$ nimmt bei $x=2$ den Wert $0$ an.
Ein Wert damit $f(g(x))=0$ gilt, ist der Wert $x=-2$ oder $x=2$ .

b) $\blacktriangleright$ Bestimme $\boldsymbol{h‘(2)}$

Du hast folgende Funktion gegeben:
$\begin{array}{rll} h(x)&=&f(x)\cdot g(x)\\ \end{array}$

Du kannst die Ableitung der Funktion $h$ mit der Produktregel bestimmen.

$\begin{array}{rll} h‘(x)&=&f‘(x)\cdot g(x)+f(x)\cdot g‘(x)\\ \end{array}$

Lies aus dem Koordinatensystem die Funktionswerte von $f(2)$ , $f‘(2)$ , $g(2)$ und $g‘(2)$ und setze diese in die Ableitung ein.
Es gilt $f(2)=-4$ . Dieser Punkt ist ein Tiefpunkt. Das bedeutet, dass die Ableitung nach der notwendigen Bedingung für ein Minimum an der Stelle $x=2$ den Wert $0$ annehmen muss. Dadurch weißt du, dass $f‘(2)=0$ ist.
Der Funktionswert $g(2)$ beträgt $0$ . Die lineare Funktion $g$ hat die Steigung $-1$ . Dies kannst du aus dem Schaubild mit Hilfe des Steigungsdreiecks bestimmen. Demnach beträgt die Ableitung $-1$ an der Stelle $x=2$ .
Nun kannst du die Werte in die Ableitung der Funktion $h$ einsetzen.

$\begin{array}{rll} h‘(2)&=&f‘(2)\cdot g(2)+f(2)\cdot g‘(2)\\ h‘(2)&=&0\cdot0+(-4)\cdot(-1)\\ h‘(2)&=&4\\ \end{array}$

Es gilt: $h‘(2)=4$

Lösung 6

a) $\blacktriangleright$ Stelle die Ebenen $\boldsymbol E$ und $\boldsymbol F$ dar

Um die Ebenen $E$ und $F$ in einem Koordinatensystem darstellen zu können, benötigst du die Spurpunkte der Ebenen.
Die Spurpunkte liegen auf den Koordinatenachsen. Der Spurpunkt der $x_1$ -Achse hat die Koordinaten $S_1(x_1\mid0\mid0)$ , der der $x_2$ -Achse $S_2(0\mid x_2\mid0)$ . Dementsprechend hat der Spurpunkt der $x_3$ -Achse die Koordinaten $S_3(0\mid0\mid x_3)$ . Du erhältst die Spurpunkte, indem du die $x$ -Werte der anderen Achsen gleich $0$ setzt und die Ebenengleichung nach deinem gewünschten $x$ auflöst.
Um den Spurpunkt $S_1$ der Ebene $E$ zu bestimmen, setzt du das $x_2=0$ . Du erhältst folgende Gleichung:

$\begin{array}{rll} x_1+x_2&=&4\\ x_1+0&=&4\\ x_1&=&4\\ \end{array}$

Der Spurpunkt $S_1$ hat demnach die Koordinaten $S_1(4\mid0\mid0)$ .
Analog dazu bestimmst du auch den Spurpunkt $S_2$ der Ebene $E$ :

$\begin{array}{rll} x_1+x_2&=&4\\ 0+x_2&=&4\\ x_2&=&4\\ \end{array}$

Dieser hat die Koordinaten $S_2(0\mid4\mid0)$ .
Bei der Ebene $F$ verfährst du genauso. Diese hat die selben Spurpunkte $S_1$ und $S_2$ wie die Ebene $E$ .
Für den Spurpunkt $S_3$ erhältst du folgendes:

$\begin{array}{rll} x_1+x_2+2x_3&=&4\\ 0+0+2x_3&=&4&\mid\; :2\\ x_3&=&2\\ \end{array}$

Du erhältst die Spurpunkte $S_1(4\mid0\mid0)$ , $S_2(0\mid4\mid0)$ und $S_3(0\mid0\mid2)$ .
Zeichne diese Punkte nun in ein Koordinatensystem ein und verbinde die Spurpunkte.

$\blacktriangleright$ Bestimme eine Gleichung der Schnittgeraden

Du weißt, dass die beiden Ebenen $E$ und $F$ die gleichen Spurpunkte $S_1$ und $S_2$ haben. Mit Hilfe der zwei Punkte kannst du eine Parametergleichung der Schnittgeraden aufstellen.
Wenn du den Punkt $S_1$ als Stützpunkt verwendest, erhältst du folgende Parametergleichung der Schnittgeraden:

$\begin{array}{rll} g:\overrightarrow{x}&=&\overrightarrow{OS_1}+t\cdot\overrightarrow{S_1S_2}\\[5pt] g:\overrightarrow{x}&=&\begin{pmatrix}4\\0\\0\end{pmatrix}+t\begin{pmatrix}0-4\\4-0\\0-0\end{pmatrix}\\[5pt] g:\overrightarrow{x}&=&\begin{pmatrix}4\\0\\0\end{pmatrix}+t\begin{pmatrix}-4\\4\\0\end{pmatrix}\\[5pt] \end{array}$

Eine Gleichung der Schnittgeraden lautet:

$\begin{array}{rll} g:\overrightarrow{x}&=&\begin{pmatrix}4\\0\\0\end{pmatrix}+t\begin{pmatrix}-4\\4\\0\end{pmatrix}\\ \end{array}$

b) $\blacktriangleright$ Gib eine Gleichung der Ebene $\boldsymbol G$ an
Die Ebene $G$ soll parallel zu der $x_1$ -Achse verlaufen. Das bedeutet, dass der Faktor vor dem $x_1$ gleich $0$ ist. Außerdem besitzt die Ebene dieselbe Spurgerade, die die $x_2x_3$ -Ebene schneidet wie die Ebene $F$ .
Die Ebene $G$ hat daher auch dieselbe Ebenengleichung wie die Ebene $F$ . Allerdings mit den Unterschied, dass der Faktor vor dem $x_1$ gleich $0$ ist.
Eine Ebenengleichung lautet:

$\begin{array}{rll} G:x_2+2x_3&=&4\\ \end{array}$

Lösung 7

$\blacktriangleright$ Bestimme den Abstand $\boldsymbol d$

Um den Abstand $d$ des Punktes $C$ von der Geraden $g$ zu bestimmen, brauchst du außer der Geradengleichung den Punkt $P$ auf der Geraden, der von $C$ den geringsten Abstand hat. Der Abstand zwischen dem Punkt $P$ und dem Punkt $C$ ist dann am geringsten, wenn die Gerade durch die zwei Punkte orthogonal auf der Geraden $g$ steht. Zwei Geraden sind orthogonal, wenn das Skalarprodukt der beiden Richtungsvektoren $0$ ergibt.
Um den Abstand zu bestimmen kannst du folgendermaßen vorgehen:

Stelle eine Geradengleichung von $g$ auf
Bestimme mit Hilfe des Skalarprodukts den Parameter $t$ der Geradengleichung und somit den Punkt $P$
Bestimme den Abstand der Punkte $P$ und $C$

1. Schritt: Aufstellen der Geradengleichung $\boldsymbol g$
Als Stützvektor wird hier der Ortsvektor $\overrightarrow{OA}$ gewählt.

$\begin{array}{rll} g:\overrightarrow{x}&=&\overrightarrow{OA}+t\cdot\overrightarrow{AB}\\[5pt] g:\overrightarrow{x}&=&\begin{pmatrix}1\\10\\1\end{pmatrix}+t\cdot\begin{pmatrix}-3-1\\13-10\\0-0\end{pmatrix}\\[5pt] g:\overrightarrow{x}&=&\begin{pmatrix}1\\10\\1\end{pmatrix}+t\cdot\begin{pmatrix}-4\\3\\0\end{pmatrix}\\[5pt] \end{array}$

2. Schritt: Bestimmung der Koordinaten des Punktes $\boldsymbol P$
Der Punkt $P$ liegt auf der Geraden $g$ . Daher hat er die von $t$ abhängigen Koordinaten $P(1-4t\mid10+3t\mid1)$ .
Das Skalarprodukt des Vektors $\overrightarrow{PC}$ und der Richtungsvektor der Geraden soll $0$ ergeben, damit sie orthogonal zueinander stehen.
Der Vektor $\overrightarrow{PC}$ lautet:

$\begin{array}{rll} \overrightarrow{PC}&=&\begin{pmatrix}2-(1-4t)\\3-(10+3t)\\1-1\end{pmatrix}\\[5pt] &=&\begin{pmatrix}2-1+4t\\3-10-3t\\0\end{pmatrix}\\[5pt] &=&\begin{pmatrix}1+4t\\-7-3t\\0\end{pmatrix}\\[5pt] \end{array}$

Skalarprodukt:

Rechenweg anzeigen

$t=-1$

Wenn du den Wert $t=-1$ in die Geradengleichung $g$ einsetzt, erhältst du die Koordinaten des Punktes $P$ .

$\begin{array}{rll} g:\overrightarrow{x}&=&\begin{pmatrix}1\\10\\1\end{pmatrix}+t\cdot\begin{pmatrix}-4\\3\\0\end{pmatrix}\\[5pt] \overrightarrow{OP}&=&\begin{pmatrix}1\\10\\1\end{pmatrix}+(-1)\cdot\begin{pmatrix}-4\\3\\0\end{pmatrix}\\[5pt] \overrightarrow{OP}&=&\begin{pmatrix}1\\10\\1\end{pmatrix}+\begin{pmatrix}4\\-3\\0\end{pmatrix}\\[5pt] \overrightarrow{OP}&=&\begin{pmatrix}5\\7\\1\end{pmatrix}\\[5pt] \end{array}$

Der Punkt $P$ hat die Koordinaten $P(5\mid7\mid1)$ .

3. Schritt: Berechnung des Abstands $\boldsymbol d$
Der Abstand $d$ zwischen den Punkten $P$ und $C$ entspricht dem Betrag des Vektors $\overrightarrow{PC}$ :

$\begin{array}{rll} d&=&\left|\overrightarrow{PC}\right|\\[5pt] d&=&\left|\overrightarrow{OC}-\overrightarrow{OP}\right|\\[5pt] d&=&\left|\begin{pmatrix}2\\3\\1\end{pmatrix}-\begin{pmatrix}5\\7\\1\end{pmatrix}\right|\\[5pt] d&=&\left|\begin{pmatrix}-3\\-4\\0\end{pmatrix}\right|\\[5pt] d&=&\sqrt{(-3)^2+(-4)^2+0^2}\\[5pt] d&=&\sqrt{9+16}\\[5pt] d&=&\sqrt{25}\\[5pt] d&=&5\\[5pt] \end{array}$

Der Punkt $C$ hat von der Geraden $g$ den Abstand $d=5$ .

Aufgabe 8

a) $\blacktriangleright$ Formuliere ein Ereignis $\boldsymbol A$

Bei dem Ereignis $A$ liegt eine Bernoulli-Kette vor. Die Formel zur Berechnung einer Wahrscheinlichkeit einer Bernoulli-Kette lautet:

Formel anzeigen

$n$ : Länge der Bernoulli-Kette
$k$ : Anzahl der Treffer
$p$ : Erfolgswahrscheinlichkeit

Schaue dir die einzelnen Terme und ihre Bedeutung an.

Das Ereignis setzt sich aus mehreren Teilen zusammen. Der erste Teile lautet: $\begin{pmatrix}10\\8\end{pmatrix}\cdot\left(\frac{2}{3}\right)^8\cdot\left(\frac{1}{3}\right)^2$

Dieser Teil gibt an, dass das Ereignis eine Kettenlänge von $10$ hat. Außerdem gibt es $8$ Treffer.
Im zweiten Teil kommt die Wahrscheinlichkeit dazu, dass man neunmal verliert. Den Ausdruck $10\cdot\left(\frac{2}{3}\right)^9\cdot\frac{1}{3}$ kann man umschreiben in $\begin{pmatrix}10\\9\end{pmatrix}\cdot\left(\frac{2}{3}\right)^9\cdot\frac{1}{3}$ .

Die $\left(\frac{2}{3}\right)^{10}$ gibt die Wahrscheinlichkeit an, dass man zehnmal verliert.
Man verliert also entweder achtmal, neunmal oder zehnmal.

Das Ereignis $A$ lautet:
$P(A)$ : Man verliert mindestens $8$ von $10$ Spielen.

b) $\blacktriangleright$ Berechne die Wahrscheinlichkeit $\boldsymbol {P(X=2)}$

Die Zufallsvariable $X$ gibt die Anzahl der verlorenen Spiele an. Die Wahrscheinlichkeit ein Spiel zu verlieren, ist bei jedem Spiel gleich groß. Die Zufallsvariable ist somit binomialverteilt und folgt somit der Bernoulli-Verteilung. Setze die Kettenlänge, Anzahl der Treffer und die Erfolgswahrscheinlichkeit in die Bernoulli-Formel ein.
Für die Erfolgswahrscheinlichkeit $p$ gilt $p=\frac{2}{3}$ . Es wird viermal gespielt, d.h. die Kettenlänge der Bernoulli-Kette beträgt $n=4$ . Der Spieler verliert genau zweimal, daher gilt: $k=2$

Setze diese Werte in die Bernoulli- Formel ein und berechne die Wahrscheinlichkeit.

Rechenweg anzeigen

$P(X=2)=\dfrac{8}{27}$

Der Spieler verliert mit einer Wahrscheinlichkeit von $\dfrac{8}{27}$ genau zweimal.

Lösung 9

$\blacktriangleright$ Beschreibe den Lösungsweg

Du hast einen Mittelpunkt $M$ einer Kugel und eine Ebene gegeben. Die Ebene berührt die Kugel in einem Berührpunkt $B$ . Eine Gerade durch die Punkte $M$ und $B$ muss demnach orthogonal zu der Ebene stehen. Der Schnittpunkt dieser Geraden mit der Ebenen entspricht dem Berührpunkt.

Um den Kugelradius und den Berührpunkt zu bestimmen, kannst du folgendermaßen vorgehen:

Stelle eine Lotgerade zu der Ebene durch den Mittelpunkt $M$ auf. Dabei dienen die Koordinaten des Punktes $M$ als Stützvektor. Der Normalenvektor der Ebene ist der Richtungsvektor der Lotgerade. \item Berechne den Schnittpunkt der Lotgerade mit der Ebene. Der Schnittpunkt entspricht dem Berührpunkt $B$ .
Berechne den Abstand der Punkte $M$ und $B$ . Der Abstand entspricht dem Kugelradius. Den Abstand berechnest du mit der Formel:

Formel anzeigen