Wahlteil C1
Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche 
Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als 
Öl enthält. Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als Öl enthält, 
und einer Standardabweichung von 
angenommen werden.
Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als Öl enthält. Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als Öl enthält,
a)
Die Rechnung 
stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung.
stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung.
(1,5 VP)
b)
An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als 780 Flaschen mindestens Öl.
Ermittle, wie viele Flaschen mindestens geliefert werden.
Öl.
Ermittle, wie viele Flaschen mindestens geliefert werden.
(1,5 VP)
c)
Ein Supermarkt erhält eine Lieferung von 150 Kartons.
Bestimme die Wahrscheinlichkeit dafür, dass mehr als 
der Kartons fehlerhaft sind.
Die Füllmenge der Flaschen soll als normalverteilt mit einem Erwartungswert von der Kartons fehlerhaft sind.
(2 VP)
und einer Standardabweichung von angenommen werden.
d)
Eine Flasche wird zufällig ausgewählt. Ermittle für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
„Die Flasche enthält mehr als 
Öl.“
„Die Füllmenge der Flasche weicht höchstens um 
vom Erwartungswert ab.“
„Die Flasche enthält mehr als Öl.“
(0,5 VP)
„Die Füllmenge der Flasche weicht höchstens um vom Erwartungswert ab.“
(1 VP)
e)
Die Füllmenge einer Flasche ist nie negativ. Die Normalverteilung, die zur Beschreibung der Füllmenge der Flaschen verwendet wird, ist jedoch auch für negative reelle Zahlen definiert und nimmt dabei ausschließlich positive Werte an.
Begründe, dass die Verwendung der Normalverteilung dennoch sinnvoll ist.
(1 VP)
f)
Das Unternehmen möchte die Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:
Vorschlag 1: Die eingestellte Füllmenge von wird erhöht.
Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von 
erreicht wird, wird erhöht.
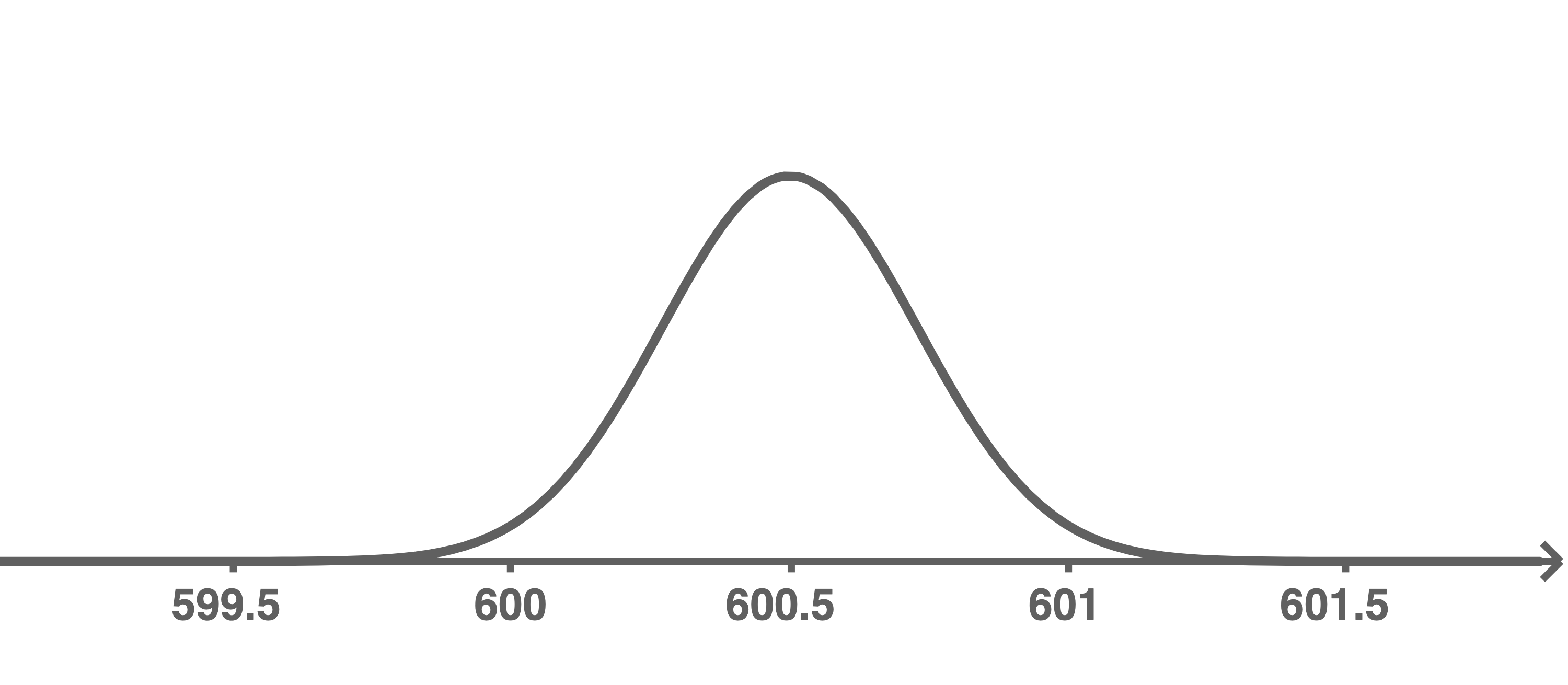
Die Abbildungen 1 und 2 zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.
Skizziere in der Abbildung 1 den Graphen einer Dichtefunktion, die sich aus dem Vorschlag 1 ergeben könnte, und in der Abbildung 2 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.
Begründe für jeden Vorschlag mithilfe des skizzierten Graphen, dass damit das Ziel des Unternehmens erreicht wird.
Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:
Vorschlag 1: Die eingestellte Füllmenge von wird erhöht.
Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von erreicht wird, wird erhöht.
Die Abbildungen 1 und 2 zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.
Skizziere in der Abbildung 1 den Graphen einer Dichtefunktion, die sich aus dem Vorschlag 1 ergeben könnte, und in der Abbildung 2 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.
Begründe für jeden Vorschlag mithilfe des skizzierten Graphen, dass damit das Ziel des Unternehmens erreicht wird.
(3 VP)
Abbildung 1
Abbildung 2
g)
Jede Flasche wird mit einem Anhänger versehen. Die Anhänger gibt es mit 
verschiedenen Motiven. Für jede Flasche wird eines dieser Motive zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass bei zufällig ausgewählten Flaschen alle Motive verschieden sind, ist kleiner als 
Ermittle den kleinsten möglichen Wert von 
verschiedenen Motiven. Für jede Flasche wird eines dieser Motive zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass bei zufällig ausgewählten Flaschen alle Motive verschieden sind, ist kleiner als
Ermittle den kleinsten möglichen Wert von
(2 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Aufgabenstellung formulieren
„Es wird ein Karton zufällig ausgewählt. Berechne die Wahrscheinlichkeit dafür, dass jede Flasche aus dem Karton mindestens 
Öl enthält."
Ansatz erläutern
Wahrscheinlichkeit dafür, dass eine Flasche mindestens enthält:
Wahrscheinlichkeit dafür, dass alle 12 Flaschen aus einem Karton mindestens enthalten:
Öl enthält."
Ansatz erläutern
Wahrscheinlichkeit dafür, dass eine Flasche mindestens enthält:
Wahrscheinlichkeit dafür, dass alle 12 Flaschen aus einem Karton mindestens enthalten:
b)
Das Mittel von mehr als 780 Flaschen entspricht dem Erwartungswert. Hierbei beschreibt die Anzahl der gelieferten Flaschen.
Es soll gelten:
![\(\begin{array}[t]{rll}
\mu&\gt& 780& \\[5pt]
n\cdot 0,985&\gt& 780&\quad \scriptsize \mid\; :0,985 \\[5pt]
n&\gt& 791,9& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2248e52758dd584db77eb251373b7654b6c9a1d6cb90f324fb6fe462053a8c36_light.svg)
Da die Anzahl der Flaschen eine natürliche Zahl sein muss, gilt 
Es werden also mindestens 792 Flaschen geliefert.
die Anzahl der gelieferten Flaschen.
Es soll gelten:
Da die Anzahl der Flaschen eine natürliche Zahl sein muss, gilt
Es werden also mindestens 792 Flaschen geliefert.
c)
beschreibt die Anzahl der Flaschen in einem Karton, die weniger als enthalten und ist binomialverteilt mit 
und 
Mit dem binomcdf-Befehl folgt:
![\(\begin{array}[t]{rll}
P(„\text{fehlerhaft}")&=& P(X \geq 2)&\quad \scriptsize \mid\; WTR \\[5pt]
&\approx& 0,013
\end{array}\)](https://www.schullv.de/resources/formulas/91de62355c1bed7d88c8fa99cf3798d25c185b0160352edfeebf33a68ec76f2b_light.svg)
beschreibt die Anzahl der fehlerhaften Kartons und ist binomialverteilt mit 
und 
der Kartons entspricht 
Da die Anzahl der Kartons eine natürliche Zahl sein muss und mehr als fehlerhaft sein sollen, müssen in diesem Fall also mindestens 5 Kartons fehlerhaft sein.
Es gilt also:
![\(\begin{array}[t]{rll}
P(Y \gt 5) &=& 1-P(Y \leq 5) \\[5pt]
&\approx & 0,05
\end{array}\)](https://www.schullv.de/resources/formulas/a3409834e56e7871d1633b3e47cb306b3bd80a2b117f7b82a3b58d2d45ed2682_light.svg)
Die Wahrscheinlichkeit dafür, dass mehr als der Kartons fehlerhaft sind, beträgt somit ca. 
d)
beschreibt die Füllmenge der Flasche in 
und ist normalverteilt mit 
und 
Mit dem normalcdf-Befehl folgt:
Ereignis A
![\(\begin{array}[t]{rll}
P(A)&=& P(Z\gt 601) & \\[5pt]
&=& 1- P(0 \leq Z\leq 601) &\quad \scriptsize \mid\; WTR \\[5pt]
&\approx& 0,015 & \\[5pt]
&=& 1,5\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/870ca4578354a37f343b7dbf9b3152986f65c5df55e038cc18be4684a609eee6_light.svg)
Ereignis B
![\(\begin{array}[t]{rll}
P(B)&=& P(600 \leq Z\leq 601) & \\[5pt]
&\approx& 0,970 & \\[5pt]
&=& 97\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/5d51cc56782782ac633f8a9cec7fa530274ddae16a27f3dad1daf4b577a678e6_light.svg)
e)
Die verwendete Normalverteilung liefert für die negativen Füllmengen so geringe Wahrscheinlichkeiten, dass diese vernachlässigt werden können.
f)
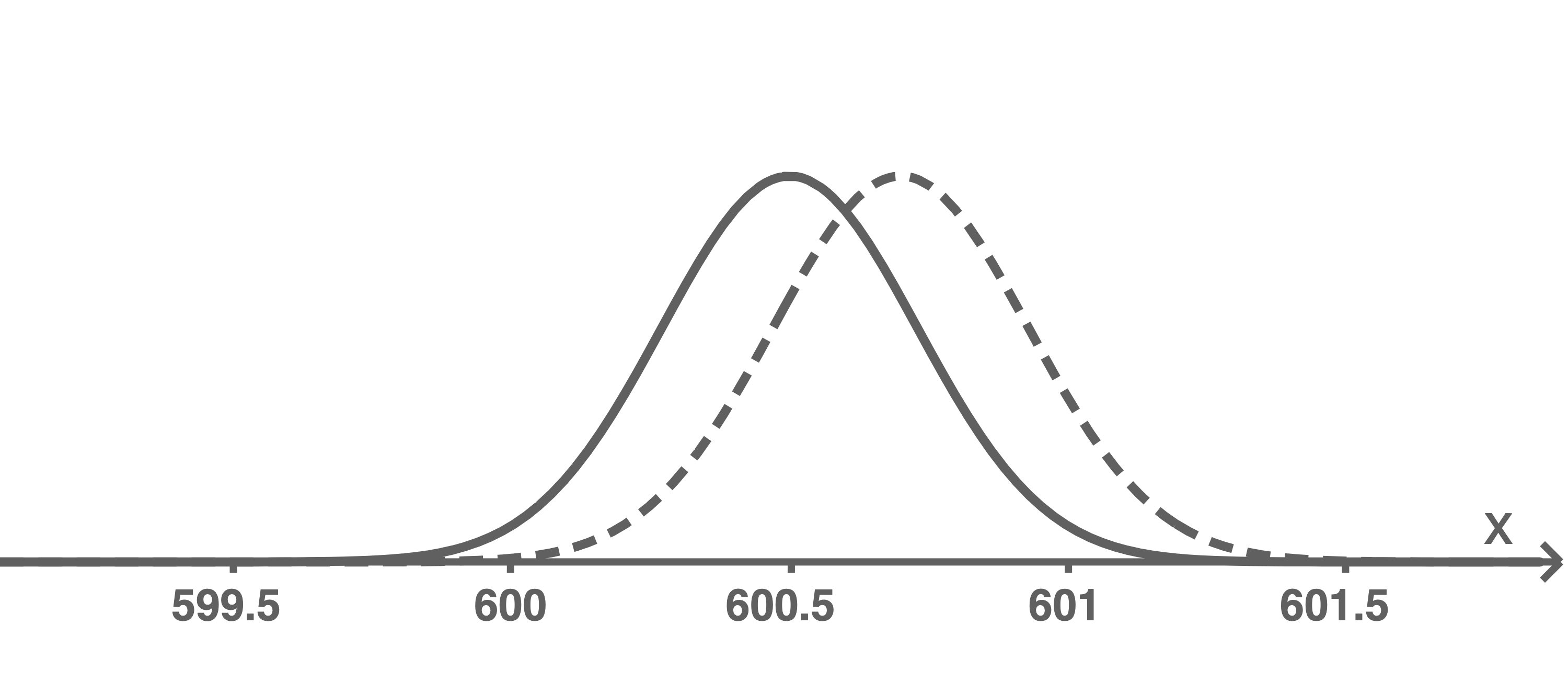
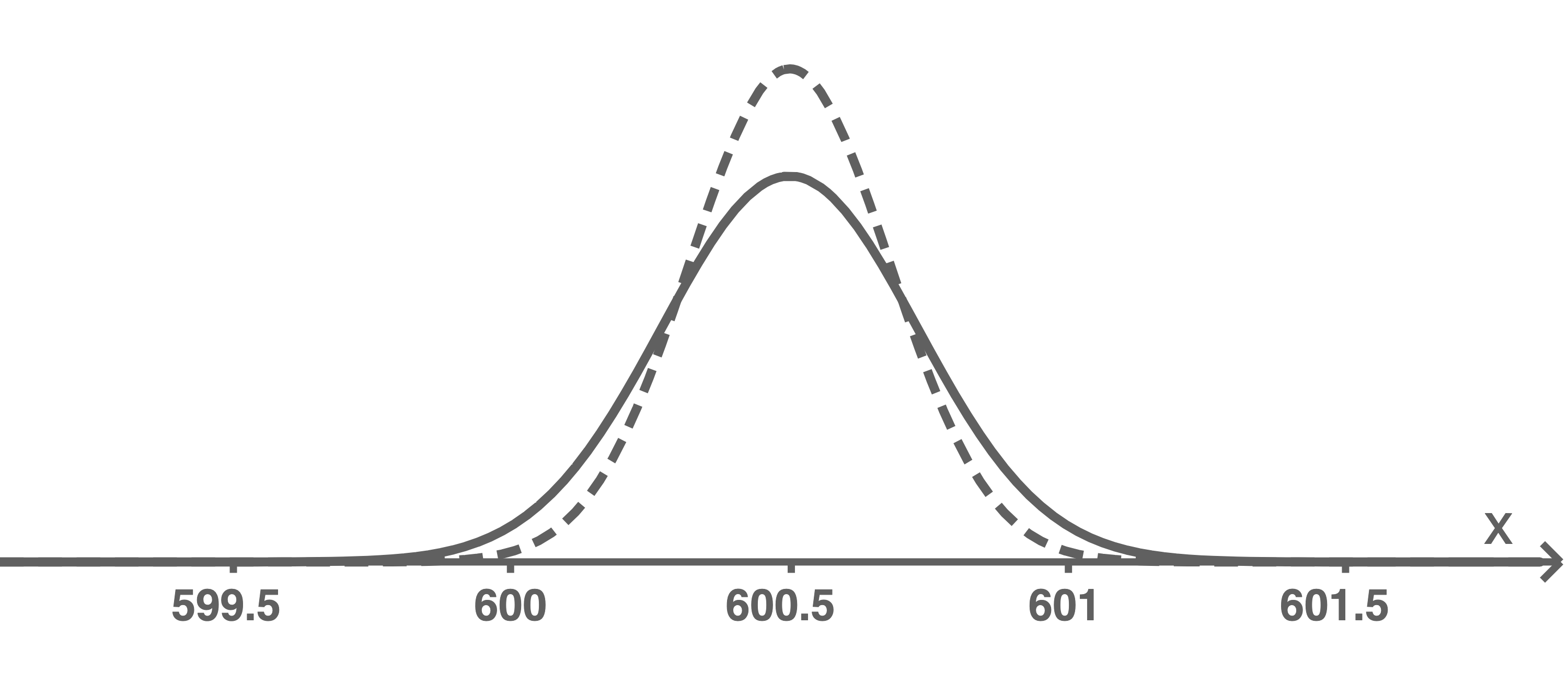
Graphen skizzieren
Mögliche Graphen für die beiden Vorschläge sind beispielsweise:
Vorschläge begründen
Der Inhalt der Fläche, die für 
zwischen dem Graphen der Dichtefunktion und der 
-Achse eingeschlossen wird, entspricht der Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält.
Beim ersten Vorschlag wird der Graph der Dichtefunktion auf der -Achse weiter entlang der positiven -Achse verschoben, sodass die darunterliegende Fläche für minimiert wird.
Durch das Strecken des Graphen der Dichtefunktion in 
-Richtung wird ebenso durch Vorschlag 2 die Fläche für unter dem Graphen reduziert.
Somit erfüllen beide Vorschläge, das Ziel, die Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält, zu verringern.
Abbildung 1
Abbildung 2
zwischen dem Graphen der Dichtefunktion und der -Achse eingeschlossen wird, entspricht der Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält.
Beim ersten Vorschlag wird der Graph der Dichtefunktion auf der -Achse weiter entlang der positiven -Achse verschoben, sodass die darunterliegende Fläche für minimiert wird.
Durch das Strecken des Graphen der Dichtefunktion in -Richtung wird ebenso durch Vorschlag 2 die Fläche für unter dem Graphen reduziert.
Somit erfüllen beide Vorschläge, das Ziel, die Wahrscheinlichkeit dafür, dass eine Flasche weniger als Öl enthält, zu verringern.
g)
Das Vorgehen beschreibt das stochastische Modell „Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge".
Für verschiedene Motive und zufällig ausgewählte Flaschen gibt es somit genau 
mögliche Kombinationen.
Wenn jede Flasche ein unterschiedliches Motiv haben soll, gibt es nach jedem Versehen einer Flasche mit einem Anhänger ein mögliches Motiv weniger für die nächsten Flaschen. Die Anzahl der möglichen Kombinationen entspricht somit 
Es folgt also:
Einsetzen verschiedener Werte für liefert 
und 
Als kleinstmöglicher Wert von ergibt sich somit 
verschiedene Motive und zufällig ausgewählte Flaschen gibt es somit genau mögliche Kombinationen.
Wenn jede Flasche ein unterschiedliches Motiv haben soll, gibt es nach jedem Versehen einer Flasche mit einem Anhänger ein mögliches Motiv weniger für die nächsten Flaschen. Die Anzahl der möglichen Kombinationen entspricht somit
Es folgt also:
Einsetzen verschiedener Werte für liefert und
Als kleinstmöglicher Wert von ergibt sich somit