Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=(3+\cos(x))^4$ .

(1,5 VP)

Aufgabe 2

Löse die Gleichung $\mathrm{e}^{4x}-5=4\mathrm e^{2x}$ .

(3 VP)

Aufgabe 3

Gegeben ist die Funktion $f$ mit $f(x)=\dfrac{2}{x^2}$ ; $x\gt 0.$

Berechne den Inhalt der markierten Fläche.

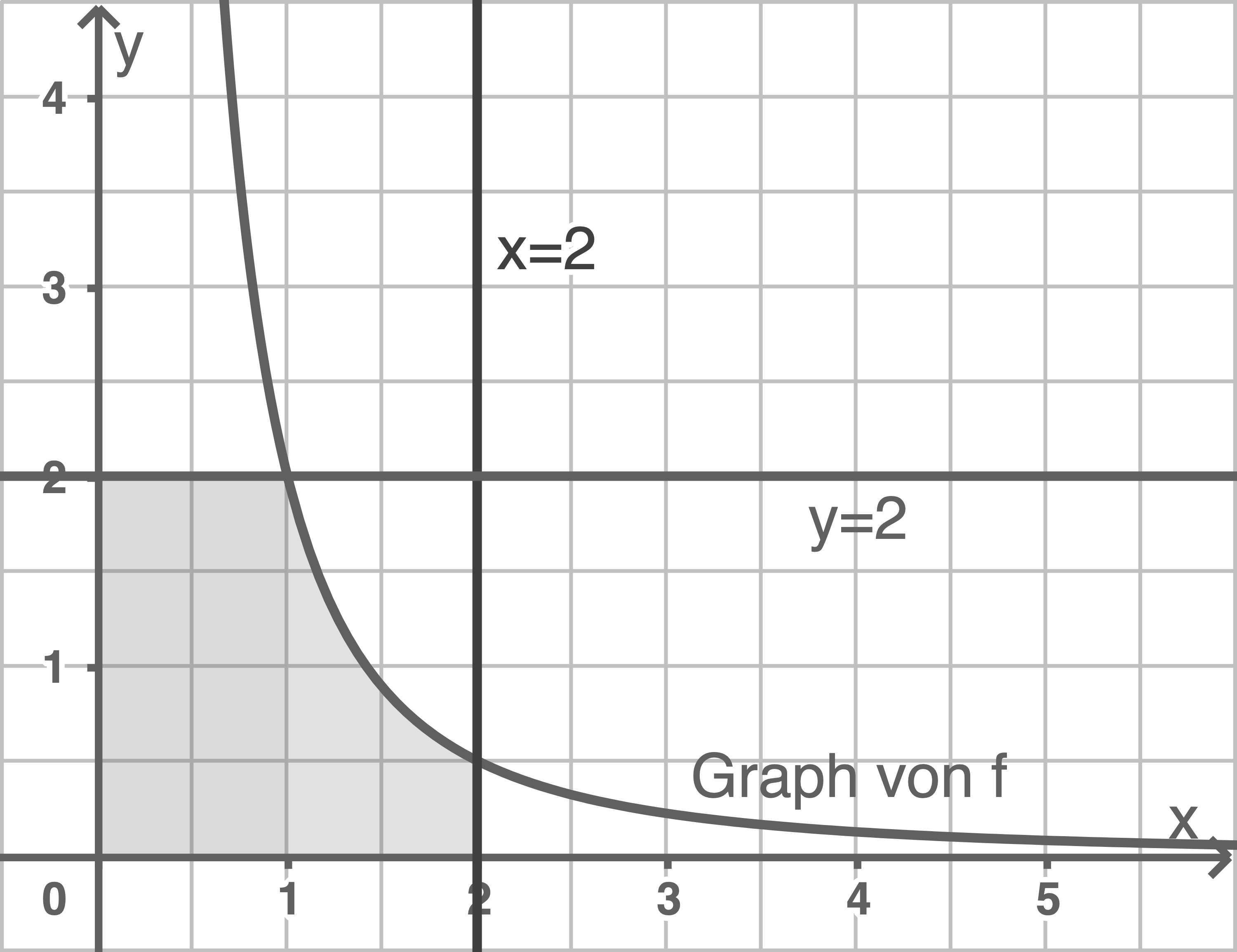
(3 VP)

Aufgabe 4

Sind folgende Aussagen wahr? Begründe jeweils deine Entscheidung.

(1) Jede Funktion, deren Ableitung eine Nullstelle hat, besitzt eine Extremstelle.
(2) Jede ganzrationale Funktion vierten Grades hat eine Extremstelle.

(2,5 VP)

Aufgabe 5

Gegeben sind die Ebenen $E: x_1+3x_2=6$ und $F: \left[ \overrightarrow{x}- \pmatrix{2\\5\\3} \right] \cdot \pmatrix{2\\0\\-1}=0$ .

Stelle die Ebene $E$ in einem Koordinatensystem dar.

Bestimme eine Gleichung der Schnittgeraden von $E$ und $F$ .

Ermittle eine Gleichung einer Geraden, die in $E$ enthalten ist und mit $F$ keinen Punkt gemeinsam hat.

(4,5 VP)

Aufgabe 6

Gegeben sind eine Ebene $E$ , ein Punkt $P$ in $E$ sowie ein weiterer Punkt $S$ , der nicht in $E$ liegt.
Der Punkt $S$ ist die Spitze eines geraden Kegels, dessen Grundkreis in $E$ liegt und durch $P$ verläuft. Die Strecke $PQ$ bildet einen Durchmesser des Grundkreises.

Beschreibe ein Verfahren, mit dem man die Koordinaten des Punktes $Q$ bestimmen kann.

(3 VP)

Aufgabe 7

In einer Urne liegen drei rote, zwei grüne und eine blaue Kugel. Es werden so lange nacheinander einzelne Kugeln gezogen und zur Seite gelegt, bis man eine rote Kugel erhält.

Bestimme die Wahrscheinlichkeit dafür, dass man höchstens drei Kugeln zieht.

(2,5 VP)

Lösung 1

Du sollst die erste Ableitungsfunktion von $f(x)=(3+ \cos(x))^4$ bestimmen. Hierbei handelt es sich um eine Verkettung mehrerer Funktionen. Hierfür benötigst du also die Kettenregel. Mit der Kettenregel folgt:

$\( \begin{array}[t]{rll} f(x)&=& (3+ \cos(x))^4 \\[5pt] f$

Lösung 2

Substitution mit $u=\mathrm{e}^{2x}$ :

$\begin{array}[t]{rll} \mathrm{e}^{4x}-5&=&4\mathrm e^{2x}\\[5pt] \left(\mathrm{e}^{2x}\right)^2-5&=& 4\mathrm{e}^{2x} \\[5pt] u^2-5&=& 4 u \quad \scriptsize \mid\; -4u \\[5pt] u^2-4u-5&=& 0 \quad \scriptsize \; \text{pq-Formel} \\[5pt] u_{1,2}&=& 2 \pm \sqrt{4+5} \\[5pt] &=& 2 \pm 3 \\[5pt] u_1&=& 5 \\[5pt] u_2&=& -1 \\[5pt] \end{array}$

Resubstitution:

$\begin{array}[t]{rll} u&=&\mathrm{e}^{2x} \quad \scriptsize \mid\; \ln(\,) \\[5pt] \ln (u)&=& 2 \cdot x \quad \scriptsize \mid\; :2 \\[5pt] \dfrac{1}{2} \ln (u)&=& x \\[5pt] x_1&=& \dfrac{1}{2} \ln (5) \\[5pt] x_2&=& \dfrac{1}{2} \ln (-1) \\[5pt] \end{array}$

$x= \dfrac{1}{2} \ln (5)$ ist einzige Lösung, da $\ln(-1)$ nicht definiert ist.

Lösung 3

Du hast die Funktion $f$ mit $f(x)=\dfrac{2}{x^2}$ mit $x \gt 0$ gegeben und sollst den Inhalt der markierten Fläche berechnen.

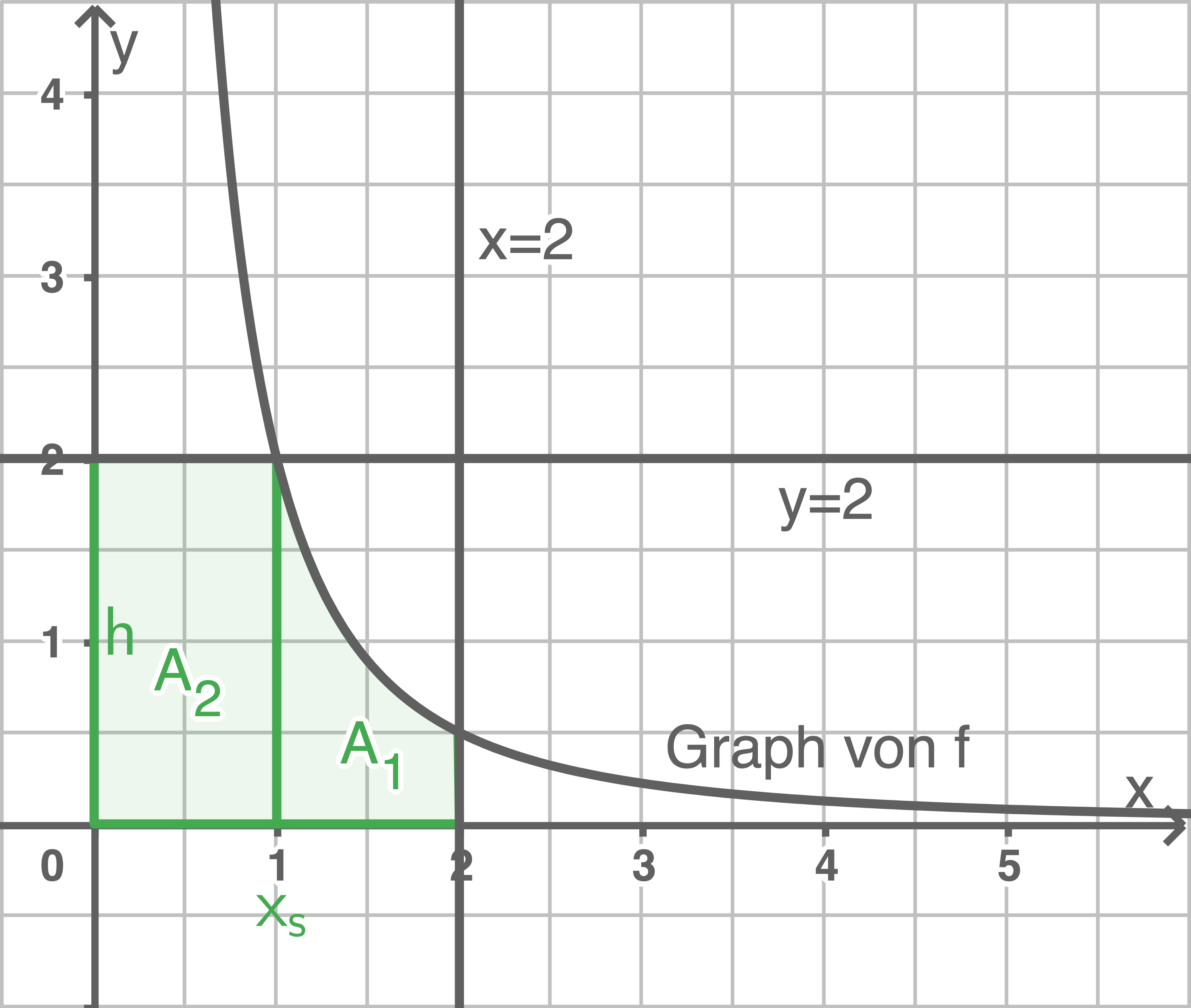
Den Flächeninhalt der markierten Fläche kannst du berechnen, indem du die Fläche in zwei Teile aufteilst. Hierzu musst du die $x$ -Koordinate des Schnittpunktes der Gerade $y=2$ und dem Graphen der Funktion $f$ berechnen. Bezeichne die $x$ -Koordinate beispielsweise mit $x_S$ .

Daraus kannst du die markierte Fläche in zwei Teile teilen. Zum einen in das Intervall auf der $x$ -Achse mit $[0;x_S]$ auf der die markierte Fläche der Form eines Rechteckes entspricht mit der Höhe $h=2 \text{ LE}$ und in das intervall $[x_S;2]$ in dem du den Flächeninhalt der Kurve unterhalb der Fläche bestimmst.

Graph einer Funktion mit Achsenbeschriftung und hervorgehobenen Bereichen A1 und A2.

Gehe somit wie folgt vor:

Bestimme die $x$ -Koordinate des Schnittpunktes $x_S$
Bestimme den Flächeninhalt unterhalb der Kurve im Intervall $[x_S;2]$
Gesamten Flächeninhalt bestimmen

1. Schritt: Koordinate des Schnittpunktes bestimmen

Du sollst zuerst die $x$ -Koordinate des Schnittpunktes zwischen dem Graphen der Funktion $f$ und der Geraden $y=2$ berechnen. Setze dazu die Funktionsterme gleich und löse nach $x$ auf. Hiermit folgt:

$\begin{array}[t]{rll} 2&=& \dfrac{2}{x^2}&\quad \scriptsize \mid\; \cdot x^2 \\[5pt] 2 \cdot x^2&=& 2 &\quad \scriptsize \mid\; :2 \\[5pt] x^2&=& 1 &\quad \scriptsize \mid\; \sqrt{\,} \\[5pt] x_1&=& 1 \\[5pt] x_2&=& -1 \\[5pt] \end{array}$

Da $x$ laut der Aufgabenstellung größer als Null sein muss, gilt für die $x$ -Koordinate des Schnittpunktes $x_S=1$ .

2. Schritt: Flächeninhalt unterhalb der Kurve bestimmen

Du sollst den Flächeninhalt im Intervall $[x_S;2]$ unterhalb der Kurve bestimmen. Für den Flächeninhalt $A_1$ unterhalb des Graphen von $f$ gilt hierbei mit den gegebenen Grenzen:

$A_1=\displaystyle\int_{x_S}^{2}f(x)\;\mathrm dx$

Damit folgt für den Flächeninhalt $A_1$ mit $x_S=1$ und $f(x)=\dfrac{2}{x^2}$ :

$\begin{array}[t]{rll} A_1&=& \displaystyle\int_{x_S}^{2} f(x)\;\mathrm dx \\[5pt] &=& \displaystyle\int_{1}^{2} \dfrac{2}{x^2} \;\mathrm dx \\[5pt] &=& \left[\dfrac{-2}{x}\right]_1^2 \\[5pt] &=& \dfrac{-2}{2} - \left(\dfrac{-2}{1}\right) \\[5pt] &=& 1 \\[5pt] \end{array}$

Somit gilt $A_1=1 \text{ FE}$ .

3. Schritt: Gesamten Flächeninhalt unterhalb der Kurve bestimmen

Der Flächeninhalt der markierten Fläche unterhalb des Graphen von $f$ setzt sich aus dem zuvor bestimmten Flächeninhalt $A_1$ zusammen und dem Flächeninhalt des Rechtecks im Intervall $[0;x_S]$ , wobei $x_S=1$ mit der Höhe $h=2$ gilt. Somit folgt für den gesamten Flächeninhalt $A$ :

$\begin{array}[t]{rll} A&=& x_S \cdot h +A_1 \\[5pt] &=& 1 \cdot 2 +1 \\[5pt] &=& 3 \\[5pt] \end{array}$

Somit gilt für den Flächeninahlt der markierten Fläche $A=3 \text{ FE}$ .

Lösung 4

(1)

Die erste Aussage lautet, dass jede Funktion, deren Ableitung eine Nullstelle hat auch eine Extremstelle besitzt. Hierzu kannst du dir mögliche Beispiele überlegen und betrachten, ob die gegebene Aussage zutrifft.

Die Aussage ist falsch, da du ein Gegenbeispiel angeben kannst. Beispielsweise die Funktion $f(x)=x^3$ besitzt die Ableitungsfunktionen $\( f$ und $\( f$ .

Dabei kannst du erkennen, dass die Ableitung bei $x=0$ eine Nullstelle besitzt, aber keinen Extrempunkt, da $\( f$ ist und somit die hinreichende Bedingung für eine Extremstelle nicht erfüllt ist.

(2)

Die zweite Aussage lautet, dass jede ganzrationale Funktion vierten Grades eine Extremstelle besitzt.

Die Notwendige Bedingung für eine Extremstelle $x_E$ lautet, dass $\( f$ gilt. Somit muss die Ableitungsfunktion an der Extremstelle eine Nullstelle besitzen.

Die hinreichende Bedingung für eine Extremstelle lautet, dass an der Nullstelle der Ableitungsfunktion ein Vorzeichenwechsel stattfinden muss. Überlege dir hierfür welche Funktionsgleichung die Ableitung besitzt.

Diese Aussage ist wahr, da die Ableitung einer ganzrationalen Funktion vierten Grades eine ganzrationale Funktion dritten Grades ist und eine ganzrationale Funktion dritten Grades immer mindestens eine Nullstelle besitzt und an mindestens einer Nullstelle ein Vorzeichenwechsel stattfinden muss.

Hierzu kannst du die Grenzwerte einer ganzrationalen Funktion dritten Grades betrachten.

Die allgemeine Funktionsgleichung einer ganzrationalen Funktion dritten Grades lautet: $f(x)=ax^3+bx^2+cx+d$ . Ist der Parameter $a$ positiv so folgt für die Grenzwertbetrachtung:

$\lim\limits_{x\to\infty} f(x)=+ \infty$ und $\lim\limits_{x\to-\infty} f(x)=- \infty$ .

Ist der Parameter $a$ negativ so gilt das umgekehrte. Daraus folgt, dass eine ganzrationale Funktion dritten Grades mindestens eine Nullstelle besitzen muss und an mindestens einer Nullstelle ein Vorzeichenwechsel stattfinden muss. Somit ist das notwendige und das hinreichende Kriterium für eine Extremstelle erfüllt und damit besitzt jede ganzrationale Funktion vierten Grades eine Extremstelle.

Lösung 5

Schnittstelle mit $x_1$ -Achse einzeichnen: $x_2=0$ ergibt $x_1=6$
Schnittstelle mit $x_2$ -Achse einzeichnen: $x_1=0$ ergibt $x_2=2$
Die Ebene ist parallel zur $x_3$ -Achse

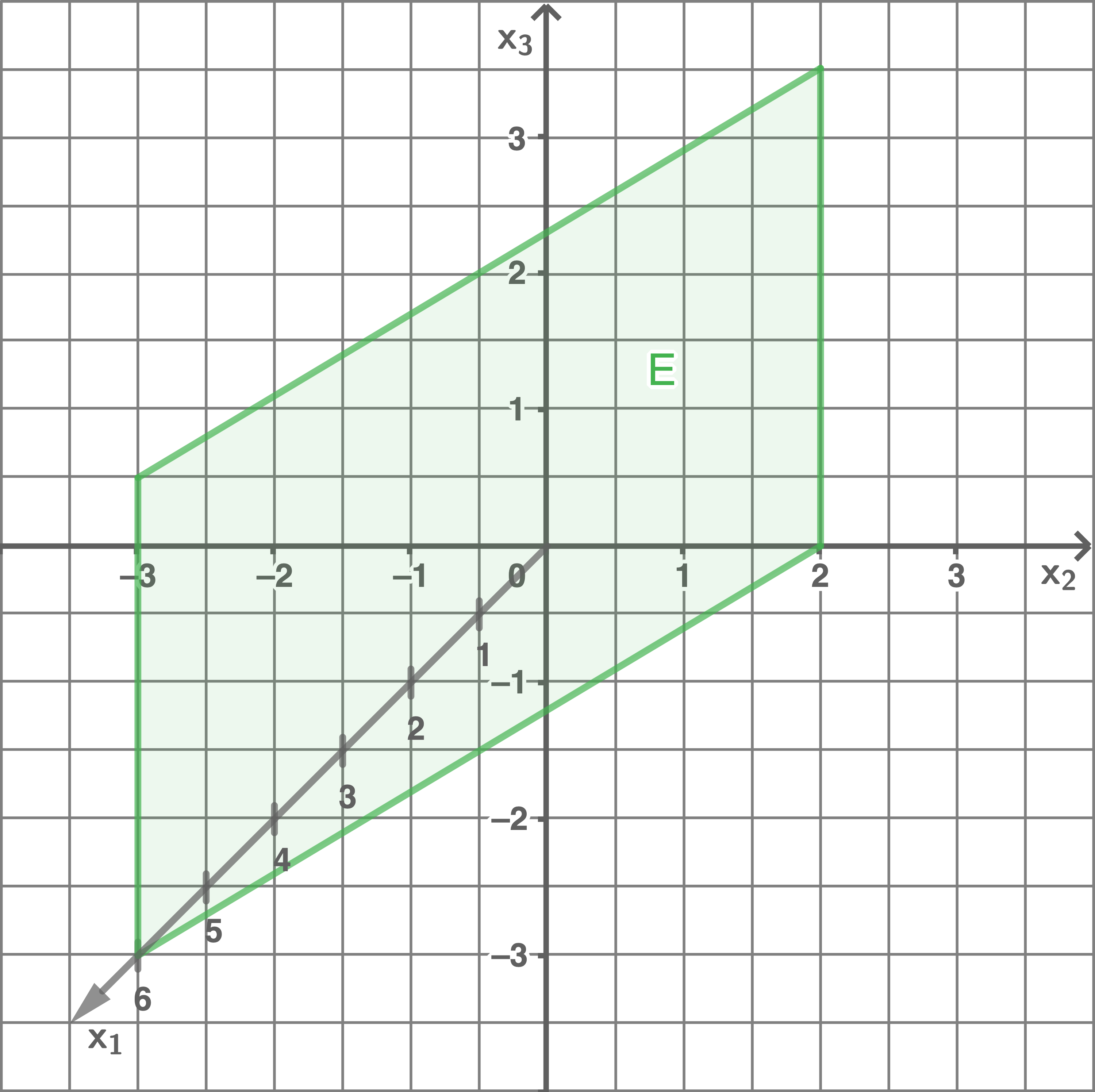
Grafische Darstellung eines Koordinatensystems mit einem eingezeichneten Bereich E und einer Linie.

$F$ in Koordinatenform-Schreibweise:

$\begin{array}[t]{rll} \left[\overrightarrow{x} - \pmatrix{2\\5\\3} \right] \cdot \pmatrix{2\\0\\-1}&=& 0\\[5pt] \pmatrix{x_1-2\\x_2-5\\x_3-3} \cdot \pmatrix{2\\0\\-1}&=& 0 \\[5pt] 2x_1-4-x_3+3 &=& 0 \\[5pt] 2x_1-x_3-1 &=& 0 \quad \scriptsize \mid\; +1\\[5pt] 2x_1-x_3 &=& 1 \end{array}$

$F: 2x_1-x_3=1$

Gleichungssystem mit $E$ und $F$ :

$\begin{array}{} \text{I}\quad& x_1+3x_2&=& 6 \\ \text{II}\quad& 2x_1 -x_3&=& 1 \\ \end{array}$

$\text{I}$ lässt sich umformen zu $x_1=6 -3x_2.$ Mit $x_2=t$ folgt $x_1=6-3t$ . Eingesetzt in $\text{II}$ ergibt sich:

$\begin{array}[t]{rll} 2\cdot (6 -3t) -x_3&=& 1 \\[5pt] 12 -6t -x_3&=& 1 \quad \scriptsize\mid\;+x_3\\[5pt] 12 -6t &=& 1 +x_3 \quad \scriptsize\mid\;-1\\[5pt] 11 -6t &=& x_3 \\[5pt] \end{array}$

Aus $x_1=6 -3t$ , $x_2=t$ und $x_3=11 -6t$ folgt: $s:\overrightarrow{x}=\pmatrix{6\\0\\11} + t \cdot \pmatrix{-3\\1\\-6}$

Die gesuchte Gerade muss parallel zu $E$ und $F$ verlaufen. Ein dazu passender Richtungsvektor ist der Richtungsvektor der Schnittgeraden: $\pmatrix{-3\\1\\-6}.$

Alternativ kann ein solcher Richtungsvektor aus dem Kreuzprodukt der beiden Normalenvektoren von $E$ und $F$ berechnet werden.

Damit die Gerade nicht in $F$ aber in $E$ liegt, wird ein Stützpunkt verwendet, der in $E$ liegt, aber nicht in $F.$

$P(6\mid 0\mid 0)$ ist in $E$ enthalten. Punktprobe mit $F$ ergibt $\left[\pmatrix{6\\0\\0}-\pmatrix{2\\5\\3}\right]\cdot\pmatrix{2\\0\\-1}=0,$ also $\pmatrix{4\\-5\\-3}\cdot\pmatrix{2\\0\\-1}=0$ und somit $8+3=0.$ Das ist nicht definiert, also liegt $P$ nicht in $F.$

$\overrightarrow{x}=\pmatrix{6\\0\\0}+s \cdot\left(\pmatrix{6\\0\\0}-\pmatrix{0\\2\\0}\right)$ $=\pmatrix{6\\0\\0}+s \cdot\pmatrix{6\\-2\\0}$

Lösung 6

Geradengleichung einer senkrechten Gerade $g$ zur Ebene $E$ durch den Punkt $S$ aufstellen
Mittelpunkt $M$ des Kreises bestimmen, der Schnittpunkt der Geraden $g$ mit der Ebene $E$ ist
Verschiebungsvektor $\overrightarrow{PM}$ aufstellen
Koordinaten des Punktes $Q$ berechnen mit der Verschiebung $\overrightarrow{OQ}=\overrightarrow{OM} + \overline{PM}$

Lösung 7

Es werden höchstens drei Kugeln gezogen, wenn entweder die erste, die zweite oder die dritte Kugel rot ist.
Anwenden der Pfadregeln:

$\frac{3}{6} + \frac{3}{6}\cdot \frac{3}{5} + \frac{3}{6}\cdot \frac{2}{5}\cdot \frac{3}{4}$ $= \frac{57}{60}$ $= \frac{19}{20}$

Mit einer Wahrscheinlichkeit von $\frac{19}{20}$ werden höchstens drei Kugeln gezogen.