Aufgabe 1.1
a)
 Bestimmen einer Koordinatengleichung für Ebene
Bestimmen einer Koordinatengleichung für Ebene
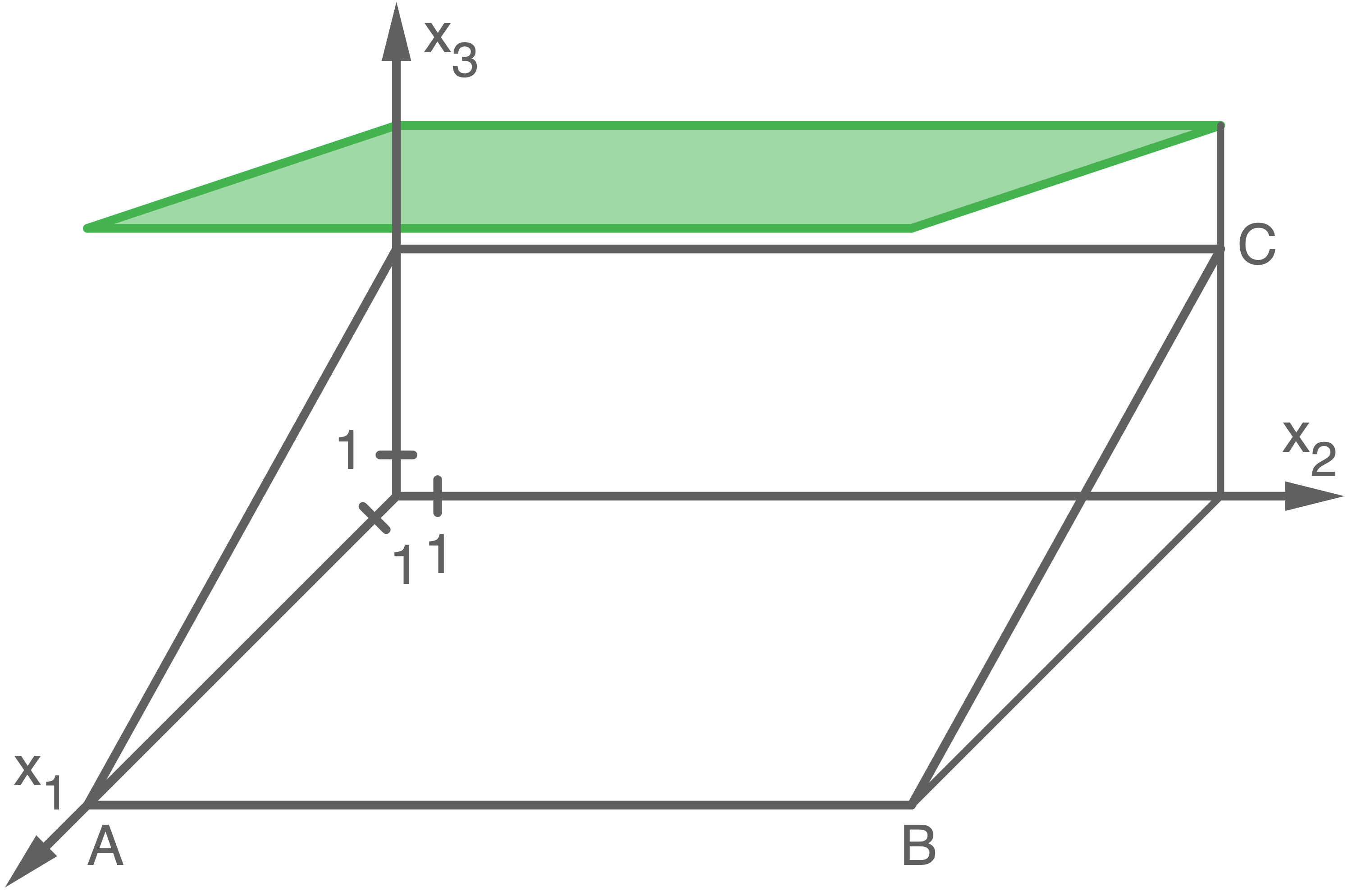
Der Aufgabenstellung kannst du entnehmen, dass die Punkte

die rechteckige Nutzfläche einer Tribüne darstellen sollen. Du sollst nun eine Koordinatengleichung der Ebene

aufstellen, in der dieses Rechteck liegt.
Eine Ebenengleichung in Koordinatenform sieht im Allgemeinen folgendermaßen aus:
Dabei ist

ein
Normalenvektor zur Ebene

, also ein Vektor, der senkrecht auf der Ebene steht. Ein solcher Normalenvektor ergibt sich aus dem
Kreuzprodukt zweier Vektoren, die in der Ebene liegen. Der Parameter

kann über eine Punktprobe bestimmt werden.
Gehe also wie folgt vor:
- Berechne einen Normalenvektor von
 mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte
mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte  ,
,  ,
,  ,
, 
- Führe eine Punktprobe durch um
 zu bestimmen
zu bestimmen
- Stelle die Ebenengleichung auf
1. Schritt: Bestimmen des Normalenvektors
Zwei Vektoren, die in

liegen erhältst du zum Beispiel mit den Verbindungsvektoren

und

:


Berechne nun

mit Hilfe des Kreuzprodukts:
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=&\overrightarrow{AB}\times \overrightarrow{AC} \\[5pt]
&=&\begin{pmatrix}0\\20\\0\end{pmatrix}\times\begin{pmatrix}-15\\20\\6\end{pmatrix} \\[5pt]
&=&\begin{pmatrix}120\\0\\300\end{pmatrix} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4268d3c6b0602236082102e3c9ff16768a206fa76a6143da61d08209e2e5decd?color=5a5a5a) 2. Schritt: Punktprobe
2. Schritt: Punktprobe
Nun lautet die bisherige Ebenengleichung

Setze dort nun die Koordinaten eines Punktes der Ebene ein und berechne so

. Wähle dazu beispielsweise

:
 3. Schritt: Ebenengleichung aufstellen
3. Schritt: Ebenengleichung aufstellen
Die Ebenengleichung in Koordinatenform lautet nun :

 Bestimmen des Winkels zwischen Nutzfläche und Erdboden
Bestimmen des Winkels zwischen Nutzfläche und Erdboden
Da das Rechteck, das die Nutzfläche der Tribüne darstellt in der Ebene

liegt und die Lage des Erdboden durch die

-Ebene beschrieben wird, ist hier der
Schnittwinkel 
dieser beiden Ebenen gesucht. Einen Schnittwinkel zwischen zwei Ebenen berechnet man allgemein über den Schnittwinkel der zugehörigen Normalenvektoren

und

.
Einen Normalenvektor von

hast du bereits im vorherigen Aufgabenteil berechnet mit

. Ein Normalenvektor der

-Ebene ist

. Damit ergibt sich nun der Schnittwinkel wie folgt:
Der Winkel zwischen der Nutzfläche der Tribüne und dem Erdboden beträgt ca.

.
 Bestimme den Inhalt der Nutzfläche
Bestimme den Inhalt der Nutzfläche
Der Inhalt der Nutzfläche ist ein Rechteck, deshalb berechnet sich der Flächeninhalt nach der Formel:
Also musst du, um den Flächeninhalt zu bestimmen, die Länge der beiden Seiten kennen. Die Länge der Seiten kannst du nun mit den Koordinaten der gegebenen Punkte bestimmen. Die Seite

kannst du als Verbindung der Punkte

und

beschreiben und die zweite Seite

als Verbindung zwischen

und

.
1. Berechnen der Länge von

Die Seite

ist die Verbindung zwischen den Punkten

und

. Hierbei musst du dir die Koordinaten der Punkte genauer anschauen.
Dabei fällt auf, dass die

- und

-Koordinaten der Punkte identisch sind. Deshalb unterscheiden sich die Punkte nur in ihrer

-Koordinate. Somit ist der Abstand zwischen den beiden Punkten die Differenz der

-Koordinate vom Punkt

und der

-Koordinate vom Punkt

. Für

gilt:

2. Berechnen der Länge von

Die Seite

ist die Verbindung zwischen den Punkten

und

. Hierbei musst du dir erneut die Koordinaten der Punkte genauer anschauen.
Dabei fällt auf, dass die

-Koordinaten der Punkte identisch ist. Deshalb unterscheiden sich die Punkte nur in ihrer

- und

-Koordinate. Somit kannst du den Abstand zwischen den beiden Punkten mit Hilfe des
Satz des Pythagoras berechnen. Der Abstand der Punkte auf der

-Achse beträgt

m und der Abstand auf der

-Achse beträgt

m. Somit gilt für

:
![\(\begin{array}[t]{rll}
b&=&\sqrt{(15\text{ m})^2+(6\text{ m})^2} \\[5pt]
&=&\sqrt{225 \text{ m}^2+36\text{ m}^2}\\[5pt]
&\approx&16,16 \text{ m}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/98a28e9371aa3652bff34c5470cdb5cf946a595143f361262fd5cef8f700d4a3?color=5a5a5a)
3. Berechnen des Inhalts der Nutzfläche

![\(\begin{array}[t]{rll}
A_N&=&a\cdot b \\[5pt]
&=&20\text{ m} \cdot 16,16\text{ m}\\[5pt]
&\approx&323\text{ m}^2\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d3c2661b8b183160af71064fb0da7fba742355b42f339a965b5b54921575f828?color=5a5a5a)
Der Inhalt der Nutzfläche beträgt ungefähr

.
b)
 Überprüfe, ob die Rückwand zwischen der Nutzfläche und der Dachfläche mind.
Überprüfe, ob die Rückwand zwischen der Nutzfläche und der Dachfläche mind.  m hoch ist.
m hoch ist.
Fertige dir für diesen Aufgabenteil zunächst eine Skizze an. Die Länge der Rückwand zwischen der Nutzfläche der Tribüne und der Dachfläche ist in der Skizze mit

bezeichnet. Der Punkt an dem die Dachfläche an der Rückwand anliegt wird mit

bezeichnet.
Damit ergibt sich folgende Skizze:
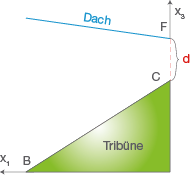 Abb. 1: Seitenansicht der Tribüne
Abb. 1: Seitenansicht der Tribüne
Um nun die Länge der Rückwand zwischen

und

zu berechnen, brauchst du die

-Koordinaten des Punktes

und des Punktes

. Die

-Koordinate des Punktes

ist bereits in der Aufgabenstellung gegeben. Über den Punkt

weißt du, dass er in der Ebene

liegt. Außerdem liegt der Punkt

bei

. Somit können wir den Wert für

in die Ebenengleichung einsetzen und die gesuchte

-Koordinate berechnen.
![\(\begin{array}[t]{rll}
x_1-3x_3 &=&-27 \\[5pt]
0-3x_3&=&-27 &\quad \mid :(-3)\\[5pt]
x_3&=&9 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4739a35ed6fd85800a2ebb31babc7bbb6c7dfd5227c29c54e13555360f6a5fb1?color=5a5a5a)
Die Länge

kann man berechnen, indem man die

-Koordinate des Punktes

von der

-Koordinate des Punktes

subtrahiert.

Da die Koordinatenangaben in Meter angegeben sind, beträgt die Länge der Rückwand zwischen der Nutzfläche der Tribüne und der Dachfläche

Meter. Somit ist die erforderliche Bedingung erfüllt.
 Koordinaten des unter Punktes an dem die Lautsprecherstütze fixiert ist
Koordinaten des unter Punktes an dem die Lautsprecherstütze fixiert ist
In dieser Aufgabe wird eine Lautsprecherstütze senkrecht zum Boden auf die Kante

montiert. Die Lautsprecherstütze ist

m lang. Nun sollst du die Koordinaten des Punktes bestimmen an dem die Lautsprecherstütze auf der Kante

fixiert wird. Da der Punkt auf der

Kante liegt, kannst du anhand der Zeichnung ablesen, dass

sein muss, da die

Koordinate auf der gesamten Kante konstant ist. Um die

- und

-Koordinate zu bestimmen fertige zuerst eine Skizze an.
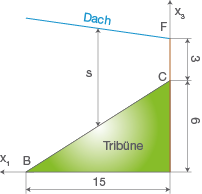 Abb. 1: Seitenansicht mit Lautsprecherstütze
Abb. 1: Seitenansicht mit Lautsprecherstütze
Die Dachfläche ist durch die Ebenengleichung

beschrieben. Möchte man also die Höhe des Daches

in Abhängigkeit der

-Koordinate angeben, so kannst du die Ebenengleichung nach

umformen, da die

-Koordinate des Daches auch exakt der Höhe entspricht.
![\(\begin{array}[t]{rll}
x_1-3x_3 &=&-27 &\quad \mid -x_1\\[5pt]
-3x_3&=&-27-x_1 &\quad \mid :(-3)\\[5pt]
x_3&=&\dfrac{1}{3} \cdot x_1 +9 \\[5pt]
h_D&=&\dfrac{1}{3} \cdot x_1 +9 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fcc917d244db684083969696f4128694c86e316420571b001d2f23219de20583?color=5a5a5a)
Nun kannst du auch die Höhe der Nutzfläche

der Tribüne als Gerade in Abhängigkeit der

Koordinate angeben. Diese kannst du durch ein Steigungsdreieck bestimmen. Für die Höhe

gilt:

Die Länge der Lautsprecherstütze

berechnet sich, indem du die Höhe der Tribüne

von der Höhe des Daches

subtrahierst.
Somit beträgt die

-Koordinate bei der die Lautsrecherstütze fixiert wird

. Jetzt musst du noch die

-Koordinate bestimmen bei der die Lautsprecherstütze fixiert ist. Dafür muss du die

-Koordinate in die Geradengleichung einsetzen, um die Höhe der Tribüne zu bestimmen.
![\(\begin{array}[t]{rll}
h_T&=&-\dfrac{6}{15} \cdot x_1 +6\\[5pt]
h_T&=&-\dfrac{6}{15} \cdot 3 +6\\[5pt]
h_T&=&4,8 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5539962712ea1a596e87dc00702912aa3b296e3271beab57d55119668f691aa2?color=5a5a5a)
Somit lautet der untere Punkt an dem die Lautsprecherstütze fixiert wird

.
Aufgabe 1.2
a)
 Wahrscheinlichkeit, dass die Augensumme bei zwei Würfen
Wahrscheinlichkeit, dass die Augensumme bei zwei Würfen  beträgt
beträgt
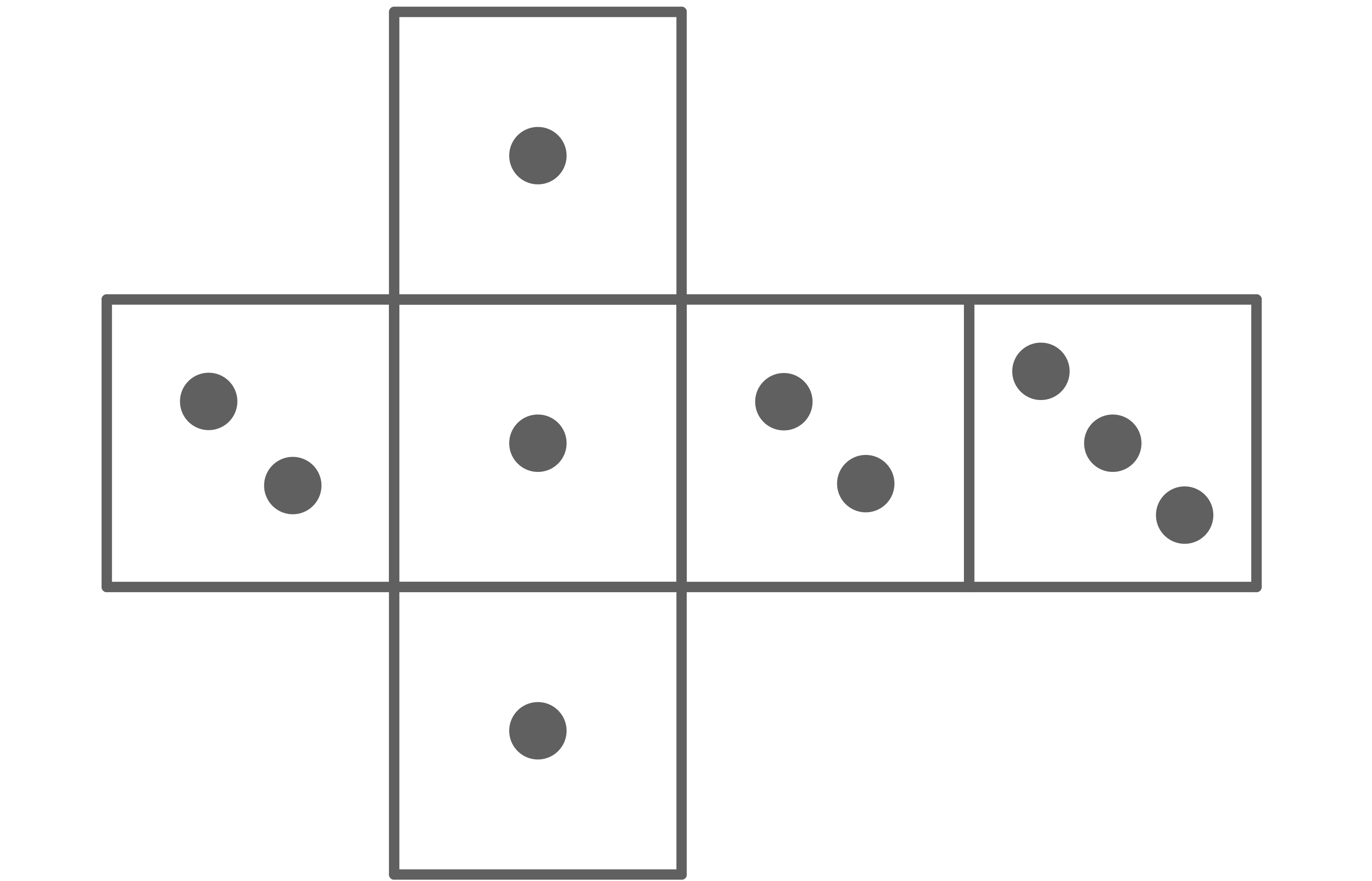
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 2 Mal mit dem Würfel geworfen wird. Du sollst nun die Wahrscheinlichkeit dafür bestimmen, dass die Augensumme der beiden Würfe

beträgt. Zuerst solltest du nun anhand der Abbildung die Wahrscheinlichkeiten für die jeweiligen Augenzahlen bestimmen. Die Wahrscheinlichkeiten sind in der nachfolgenden Tabelle eingetragen.
Die Augensumme der beiden Würfe kann nur für die zwei nachfolgenden Fälle

betragen:
1. Fall: Du würfelst beim ersten Wurf eine

und beim zweiten Wurf eine
 2. Fall:
2. Fall: Du würfelst beim ersten Wurf eine

und beim zweiten Wurf eine

Nun kannst du die Wahrscheinlichkeiten für den jeweiligen Fall bestimmen und die Wahrscheinlichkeiten anschließend addieren. Da sich die Wahrscheinlichkeiten bei mehrmaligem Würfeln nicht verändern sind die Wahrscheinlichkeiten für die beiden Fälle identisch. Die Wahrscheinlichkeit einer der beiden Fälle berechnet sich indem du die Wahrscheinlichkeit eine

zu würfeln mit der Wahrscheinlichkeit eine

zu würfeln multiplizierst.
Somit ergibt sich für die Wahrscheinlichkeit dafür, dass die Augensumme

beträgt:
 Wahrscheinlichkeit, dass mind 4-mal die Augenzahl
Wahrscheinlichkeit, dass mind 4-mal die Augenzahl  erscheint
erscheint
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 12-mal der Würfel geworfen wird. Der Würfel verändert sich hierbei nicht, weswegen sich auch die Wahrscheinlichkeiten nicht ändern. Der Würfel besitzt die Augenzahlen

,

und

mit oben angegebenen Wahrscheinlichkeiten. Deine Aufgabe ist es nun, die Wahrscheinlichkeit dafür zu bestimmen, dass bei 12-mal würfeln mindestens 4-mal die Augenzahl

geworfen wird.
Willst du hier diese Wahrscheinlichkeit bestimmen, so betrachtest du zunächst die Zufallsvariable

. Zufallsvariable

beschreibt die geworfene Augenzahl. Da bei diesem Zufallsversuch nur die Höhe der Augenzahl relevant ist und sich die Wahrscheinlichkeiten nicht ändern, ist die Zufallsvariable
 binomialverteilt
binomialverteilt. Da insgesamt

Mal gewürfelt wird, ist

.
Die Wahrscheinlichkeit

kannst du aus der obigen Tabelle ablesen. Da hier die Wahrscheinlichkeit dafür gesucht wird, dass mindestens 4 Mal die Augenzahl

gewürfelt wird, muss für die Zufallsvariable

hier folgendes gelten:

.
Diese Wahrscheinlichkeit kannst du mit deinem CAS berechnen. Dazu musst du den
binomCdf-Befehl verwenden. Da dieser aber nur Ausdrücke wie

berechnen kann, musst du hier zunächst wie folgt das Gegenereignis zu

bilden:
Die Wahrscheinlichkeit die Augenzahl

zu würfeln beträgt:
 .
.
Nun weißt du, dass

,

gilt. Wende den
binomCdf-Befehl wie in den Schaubildern unten an, um hier die gesuchte Wahrscheinlichkeit zu berechnen. Greife dazu aber zunächst über
Menü

6: Statistik

5: Verteilungen

E: Binomial Cdf
auf diesen zu.
Die Wahrscheinlichkeit, mindestens 4-mal die Augenzahl

zu würfeln beträgt also etwa 60,7 %.
 Wahrscheinlichkeit eine
Wahrscheinlichkeit eine  zu würfeln
zu würfeln
In dieser Teilaufgabe sollst du bestimmen, wie viele Seiten mindestens mit einer

beschriftet sein müssen, damit man bei 12-mal würfeln mit mindestens

Wahrscheinlichkeit mindestens 4-mal die Augenzahl

würfelt. Da der Würfel

Seiten besitzt hast du die Möglichkeit, dass der Würfel mit

,

,

,

,

,

oder

Seiten mit der Augenzahl

beschriftet ist. Je nach Anzahl der beschrifteten Seiten verändert sich also die Wahrscheinlichkeit, die Augenzahl

zu würfeln. Um nun die passende Wahrscheinlichkeit und damit auch die Anzahl der beschrifteten Seiten herauszufinden, musst du für die jeweiligen Wahrscheinlichkeiten das Ergebnis überprüfen. Da hierbei wieder

Mal gewürfelt wird ist

.
Für das Gegenereignis kannst du nun die Wahrscheinlichkeit wie oben aufstellen:

Nun sollst du

in Abhängigkeit von

angeben. Dazu gehe zunächst in den Modus

. Dort trägst du nun den unten angegebenen Ausdruck mit den Werten bei
2nd

DISTR

B:binomcdf(
an.
Nun kannst du mit
2nd  table
table in den Tabellenmodus wechseln. Dort angekommen kannst du mit
2nd  tbl set
tbl set die Einstellungen auf folgende Werte ändern. Wenn du nun erneut in den Tabellenmodus wechselst, kannst du

als

ablesen und die zugehörige Wahrscheinlichkeit

als

.
 Abb. 7: Einstellungen für die Tabelle
Abb. 7: Einstellungen für die Tabelle
Nun kannst du an der Tabelle ablesen, dass bei


ist. Das bedeutet, dass bei einer Wahrscheinlichkeit von


ist. Somit müssen mindestens

Seiten mit der Augenzahl

beschriftet werden.
b)
 Entscheidungsregel formulieren
Entscheidungsregel formulieren
Du sollst hier eine Entscheidungsregel formulieren, das heißt eine Regel dafür formulieren, ob die Behauptung des Spielers, dass der Würfel aus der oberen Aufgabe zu oft die Augenzahl

zeigt. Dabei ist die Nullhypothese vorgegeben. Für die Nullhypothese gilt:

Es wird also ein
rechtsseitiger Hypothesentest auf dem gegebenen Signifikanzniveau

durchgeführt.
Wir betrachten hier die Zufallsvariable

, die die Höhe der Augenzahl beschreibt. Diese ist binomialverteilt mit den gegeben Parameter

und

. Da ein linksseitiger Hypothesentest durchgeführt wird, wird die Nullhypothese nur für kleine Werte abgelehnt.
Der Ablehnungsbereich hat daher die Form
![\(\overline{K} = [k,n]\)](https://mathjax.schullv.de/391043bd7a1f8e2c5198c686db10fef5c98ac035cccbfec734d33fb0ea724350?color=5a5a5a)
.
Du musst nun also die Grenze

des Ablehnungsbereichs bestimmen, um sagen zu können, für welche Werte die Nullhypothese verworfen werden kann. Hierfür musst du das Signifikanzniveau nutzen. Dies gibt die
Irrtumswahrscheinlichkeit an, also genau die Wahrscheinlichkeit dafür, dass die Nullhypothese gilt und die Stichprobe trotzdem einen Wert aus dem Ablehnungsbereich liefert. Es ist also das kleinste

gesucht, welches gerade noch folgende Ungleichung erfüllt:

Zum Lösen kannst du den BinomCdf-Befehl deines GTR verwenden. Gib die Funktion

im

-Menü des GTR über den BinomCdf-Befehl ein. Diesen findest du unter
2ND  VARS(DISTR)
VARS(DISTR)  B: BinomCdf
B: BinomCdf
In die Klammern musst du dann die Parameter eingeben:

,

und

. Anschließend kannst du dir mit dem folgenden Befehl die Wertetabelle anzeigen lassen.
2ND  GRAPH(TABLE)
GRAPH(TABLE)
Wähle dann aus dieser Tabelle das größte

, sodass

gerade noch kleiner oder gleich

ist. Du findest folgende Werte:

und

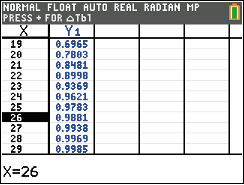 Abb. 9: Tabelle
Abb. 9: Tabelle
Damit ist das gesuchte

und die Entscheidungsregel lässt sich wie folgt formulieren:
Wird höchstens

-mal die Augenzahl

gewürfelt, so wird die Nullhypothese angenommen und die Behauptung des Spielers auf dem Signifikanznieveau

ist nicht zutreffend. Wird aber mehr als

-mal die Augenzahl

gewürfelt, so wird die Nullhypothese verworfen und die Behauptung des Spielers auf dem Signifikanzniveau

stimmt.
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
 ,
,  und
und  Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben in Meter).
Eckpunkte der rechteckigen Nutzfläche einer Tribüne (alle Koordinatenangaben in Meter).
 -Ebene stellt den Erdboden dar. Die Eckpunkte der Dachfläche liegen vertikal über den Eckpunkten der Nutzfläche. Die Dachfläche liegt in der durch
-Ebene stellt den Erdboden dar. Die Eckpunkte der Dachfläche liegen vertikal über den Eckpunkten der Nutzfläche. Die Dachfläche liegt in der durch  beschriebenen Ebene (siehe Abbildung).
beschriebenen Ebene (siehe Abbildung).
 hoch sein.
hoch sein.
 lange, senkrecht zum Erdboden verlaufende Stütze montiert. Ihre Enden werden an der Kante
lange, senkrecht zum Erdboden verlaufende Stütze montiert. Ihre Enden werden an der Kante  und am Dach der Tribüne fixiert.
und am Dach der Tribüne fixiert.
 , in dem das untere Ende der Stütze fixiert wird.
, in dem das untere Ende der Stütze fixiert wird.

 -mal geworfen.
-mal geworfen.
 beträgt.
beträgt.
 -mal geworfen.
-mal geworfen.
 -mal die Augenzahl
-mal die Augenzahl  zeigt.
Die Beschriftung des Würfels soll so geändert werden, dass man bei
zeigt.
Die Beschriftung des Würfels soll so geändert werden, dass man bei  -maligem Werfen des Würfels mit mindestens
-maligem Werfen des Würfels mit mindestens 
 Wahrscheinlichkeit mindestens
Wahrscheinlichkeit mindestens  -mal die Augenzahl
-mal die Augenzahl  erhält.
erhält.
 mindestens stehen?
mindestens stehen?
 zeigt. Die Nullhypothese
zeigt. Die Nullhypothese
 : „Die Wahrscheinlichkeit für die Augenzahl
: „Die Wahrscheinlichkeit für die Augenzahl  beträgt höchstens
beträgt höchstens  .“
.“
 Würfen auf einem Signifikanzniveau von
Würfen auf einem Signifikanzniveau von 
 getestet werden.
getestet werden.
mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte
,
,
,
zu bestimmen
 Abb. 1: Seitenansicht der Tribüne
Abb. 1: Seitenansicht der Tribüne
 Abb. 1: Seitenansicht mit Lautsprecherstütze
Abb. 1: Seitenansicht mit Lautsprecherstütze
.
 6: Statistik
6: Statistik  5: Verteilungen
5: Verteilungen  E: Binomial Cdf
E: Binomial Cdf
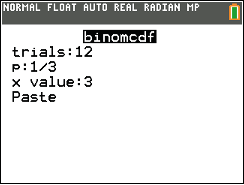 Abb. 3: Eingetragene Daten
Abb. 3: Eingetragene Daten
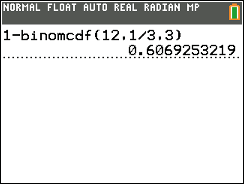 Abb. 4: Ergebnis
Abb. 4: Ergebnis
 DISTR
DISTR  B:binomcdf(
B:binomcdf(
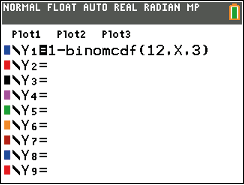 Abb. 5: Ausdruck
Abb. 5: Ausdruck
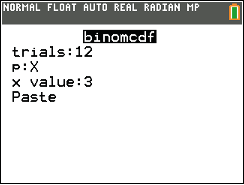 Abb. 6: Eingetragene Daten
Abb. 6: Eingetragene Daten
 Abb. 7: Einstellungen für die Tabelle
Abb. 7: Einstellungen für die Tabelle
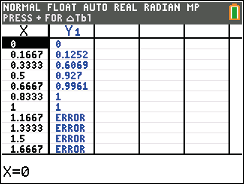 Abb. 8: Tabelle
Abb. 8: Tabelle
 Abb. 9: Tabelle
Abb. 9: Tabelle
mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte
,
,
,
zu bestimmen
 Abb. 1: Seitenansicht der Tribüne
Abb. 1: Seitenansicht der Tribüne
 Abb. 1: Seitenansicht mit Lautsprecherstütze
Abb. 1: Seitenansicht mit Lautsprecherstütze
.
 DISTR
DISTR  B:binomcdf(
B:binomcdf(
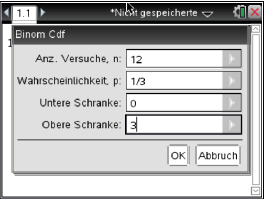 Abb. 3: Eingetragene Daten
Abb. 3: Eingetragene Daten
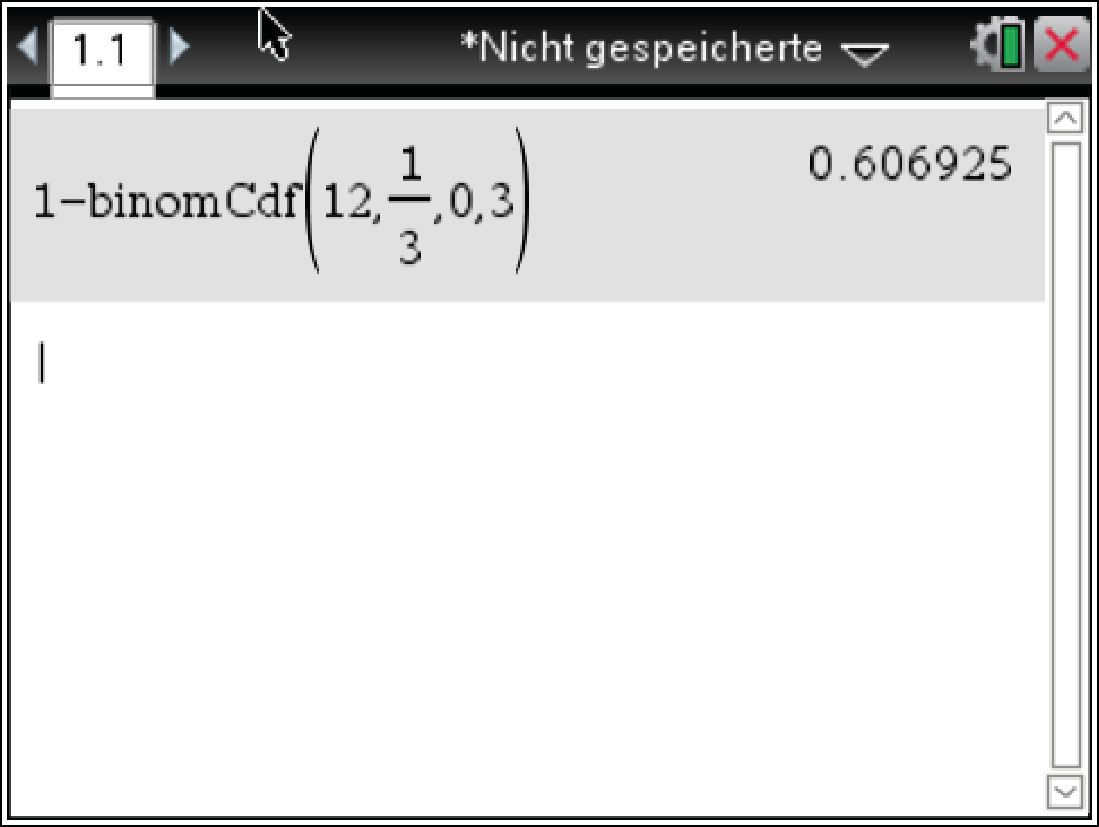 Abb. 4: Ergebnis
Abb. 4: Ergebnis
 6: Statistik
6: Statistik  5: Verteilungen
5: Verteilungen  E: Binomial Cdf.
E: Binomial Cdf.
 Abb. 5: Ergebnisse
Abb. 5: Ergebnisse
 6: Statistik
6: Statistik  5: Verteilungen
5: Verteilungen  E: Binomial Cdf.
E: Binomial Cdf.
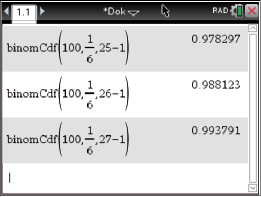 Abb. 6: Ergebnisse
Abb. 6: Ergebnisse