Analytische Geometrie

Aufgabe II 1

Abbildung 1 zeigt die Pyramide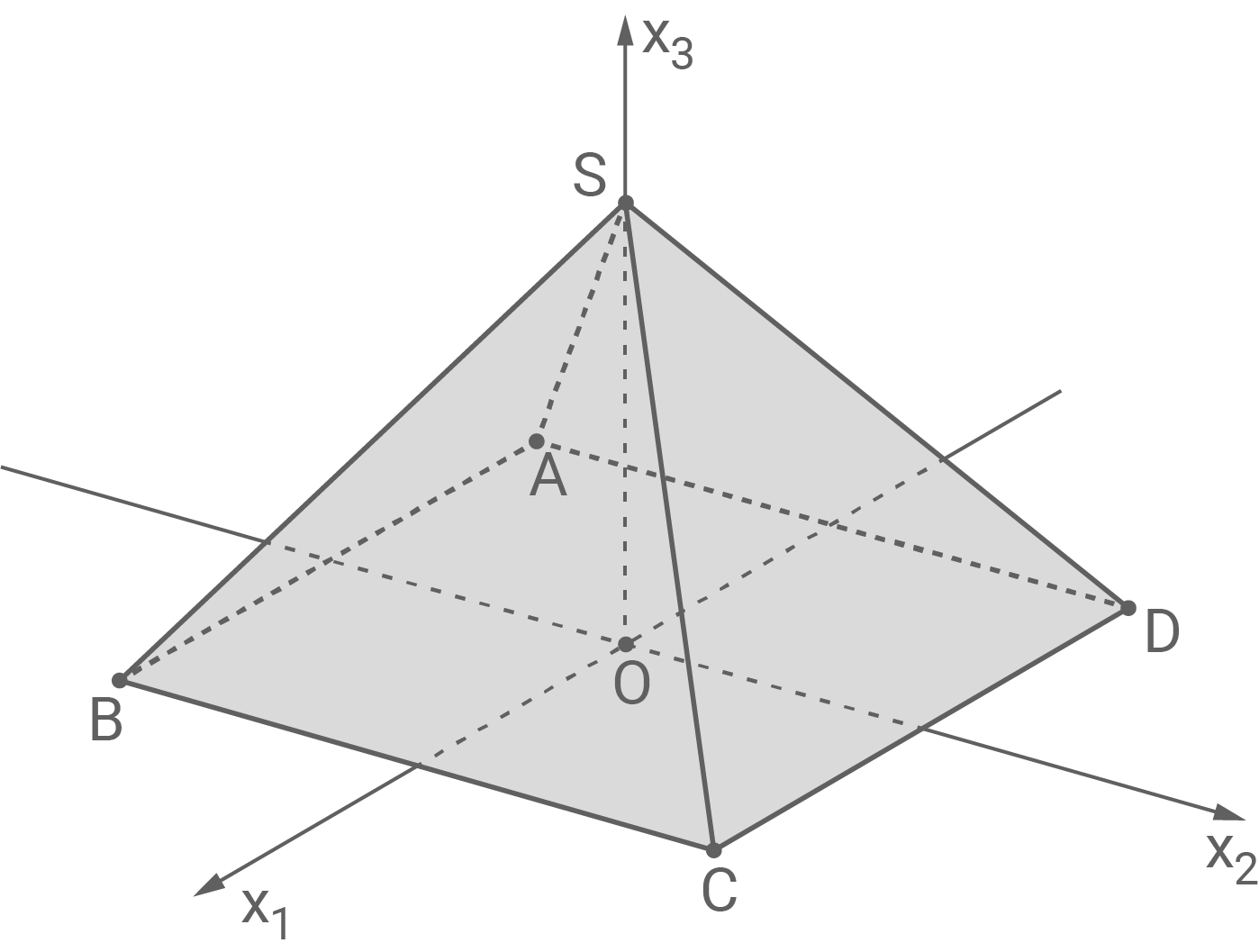 $ABCDS$ mit den Eckpunkten $A(-3\mid-3\mid 0),$ $B(3\mid-3\mid 0),$ $C(3\mid3\mid 0),$ $D(-3\mid 3\mid 0)$ und $S(0\mid0\mid 4)$ sowie den Punkt $O(0\mid 0\mid 0),$ der in der quadratischen Grundfläche der Pyramide liegt.

Die Seitenfläche $CDS$ der Pyramide liegt in der Ebene $E.$

Pyramide kartesisches Koordinatensystem Mathe Abi 2024

Abbildung 1

Berechne den Inhalt der Oberfläche der Pyramide.

(4 BE)

Genau eine der folgenden Gleichungen $(1)$ bis $(3)$ beschreibt eine Symmetrieebene der Pyramide.

Gib diese Gleichung an und begründe für eine der anderen Gleichungen, dass die durch sie beschriebene Ebene keine Symmetrieebene der Pyramide ist.

$(1) \quad x_1-x_3=0$

$(2) \quad x_1+x_2+x_3=4$

$(3) \quad x_1+x_2=0$

(3 BE)

Bestimme eine Gleichung von $E$ in Koordinatenform.

(zur Kontrolle : $\; 4 x_2+3 x_3=12$ )

(3 BE)

Es gibt einen Punkt $P(0\mid0\mid p),$ der im Innern der Pyramide liegt und von allen vier Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat.

Mit Hilfe des folgenden Gleichungssystems lässt sich der Wert von $p$ bestimmen:

$(\text{I}) \quad \overrightarrow{OQ}=\pmatrix{0\\0\\p}+t\cdot \pmatrix{0\\4\\3}$ $\quad \quad (\text{II}) \quad 4 \cdot 4 t+3 \cdot(p+3 t)=12$ $\quad \quad (\text{III})\quad |\overrightarrow{P Q}|=p$

Erläutere die Überlegungen im geometrischen Zusammenhang, die diesem Vorgehen zur Bestimmung des Werts von $p$ zugrunde liegen.

(5 BE)

Die Ebene $E$ aus Aufgabe $c$ gehört zur Schar der Ebenen $E_k: 4 k \cdot x_1+4 \sqrt{1-k^2} \cdot x_2+3 \cdot x_3=12$ mit $k \in[-1 ; 1].$

Die Seitenfläche $A D S$ der Pyramide liegt in der Ebene $E_{-1}$ der Schar, die Seitenfläche $B C S$ in der Ebene $E_1.$

Zeige, dass der Punkt $S$ in allen Ebenen der Schar enthalten ist.

(1 BE)

Weise nach, dass die Größe des Winkels, unter dem die Gerade $OS$ die Ebene $E_k$ schneidet, unabhängig von $k$ ist.

(3 BE)

Jede Ebene $E_k$ der Schar schneidet die $x_1x_2$ -Ebene in einer Gerade $g_k.$ Mit $R_k$ wird jeweils derjenige Punkt auf $g_k$ bezeichnet, der von $O$ den kleinsten Abstand hat.

In Abbildung 2 sind $g_k$ und $R_k$ beispielhaft für eine Ebene $E_k$ der Schar dargestellt.

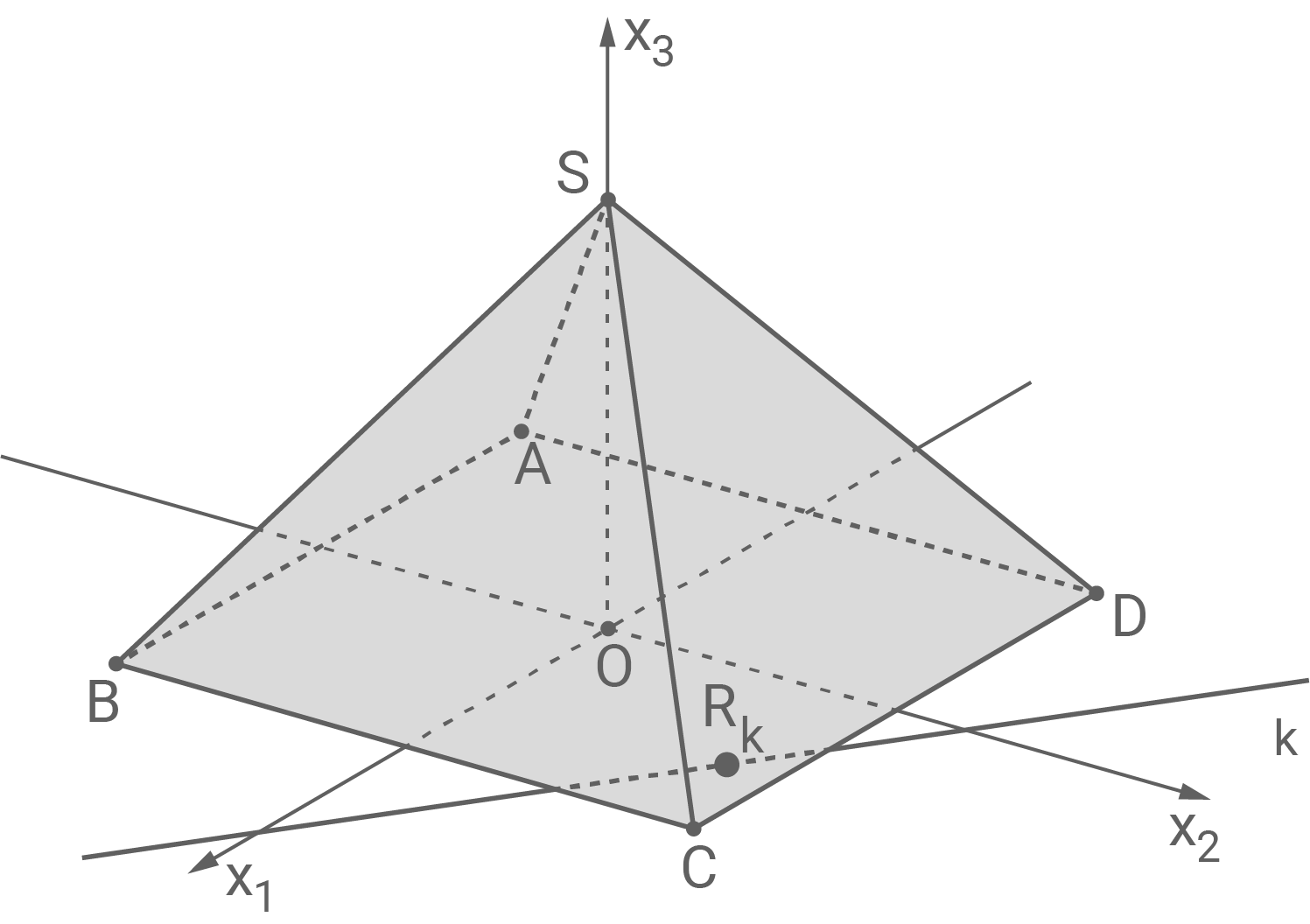
Abbildung 2

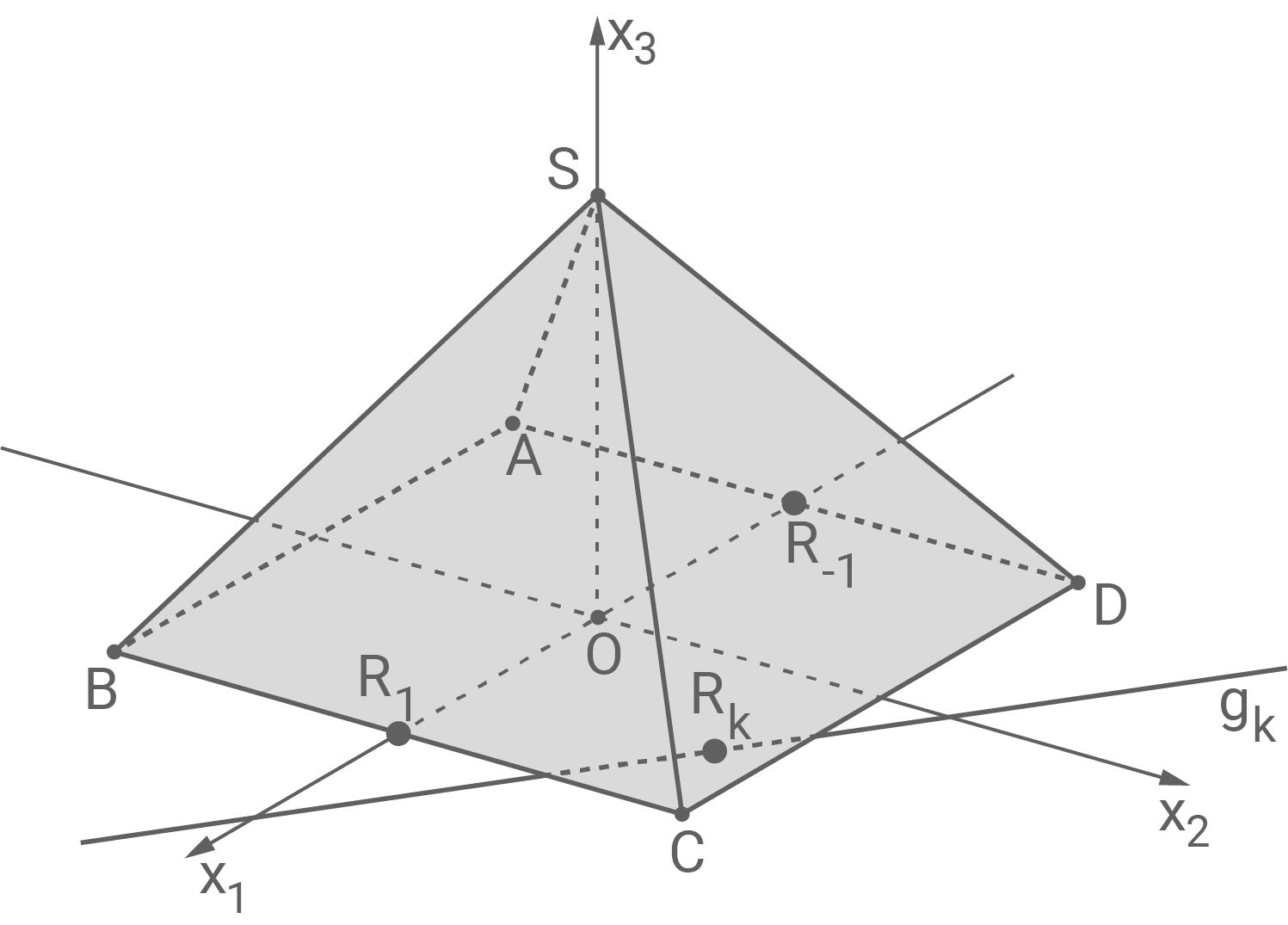
Zeichne die Punkte $R_{-1}$ und $R_1$ in Abbildung 2 ein.

(2 BE)

Durchläuft $k$ alle Werte von $-1$ bis $1,$ dann dreht sich die Fläche $O R_k S$ um die Strecke $\overline{OS}.$ Dabei entsteht ein Körper.

Beschreibe die Form des entstehenden Körpers und bestimme das Volumen dieses Körpers.

(3 BE)

Aufgabe II 2

Gegeben sind die Ebene $E: \; 3 x_1-6 x_2+2 x_3=12$ und die Schar der Geraden $g_a: \overrightarrow{x}=\pmatrix{1\\2\\5}+t\cdot \pmatrix{a\\1\\a-2}, \; t \in \mathbb{R}, \; a \in \mathbb{R}.$

Untersuche, ob $g_4$ orthogonal zu $g_{0,5}$ ist.

(2 BE)

Berechne die Größe des Winkels, den $g_4$ mit $E$ einschließt.

(3 BE)

Untersuche, ob eine Gerade der Schar den Ursprung enthält.

(3 BE)

Alle Geraden der Schar liegen in der Ebene $F.$

Ermittle eine Koordinatengleichung von $F.$

(zur Kontrolle : $x_1-2 x_2-x_3=-8$ )

(4 BE)

Betrachtet werden die Punkte $P_r(1+r\mid 2-2 r\mid 5-r)$ mit $r \in \mathbb{R}_0^{+}.$

Begründe, dass die Punkte $P_r$ auf einer zu $F$ orthogonalen Gerade liegen.

(3 BE)

Beurteile die folgende Aussage:

Jeder Punkt $P_r$ hat von jeder Gerade der Schar den Abstand $\sqrt{6} \cdot r.$

(4 BE)

Gegeben ist die Gerade $k: \overrightarrow{x}=\pmatrix{1\\2\\5}+s \cdot \pmatrix{1\\0\\1}, s \in \mathbb{R}.$

Zeige, dass $k$ in $F$ liegt, aber nicht zur Schar gehört.

(3 BE)

Die Schnittpunkte aller Geraden $g_{a}$ mit der $x_1x_2$ -Ebene liegen auf der Gerade $h.$

Auf $h$ gibt es einen Punkt, der auf keiner Gerade $g_a$ liegt.

Bestimme die Koordinaten dieses Punkts.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung II 1

Da die Kanten der Grundseite der Pyramide parallel zur $x_1$ - bzw. $x_2$ -Achse verlaufen und die Koordinaten der vier Eckpunkte $A,B,C$ und $D$ die Form $(\pm3\mid\pm3\mid0)$ haben, folgt die Seitenlänge der quadratischen Grundfläche mit $6\;[\text{LE}].$

Für den Ortsvektor des Mittelpunkts $M$ der Strecke $\overline{BC}$ folgt:

$\begin{array}[t]{rll} \overrightarrow{OM}&=&\overrightarrow{OB}+\dfrac{1}{2}\cdot\overrightarrow{BC} \\[5pt] &=&\pmatrix{3\\-3\\0}+\dfrac{1}{2}\cdot\pmatrix{3-3\\3-(-3)\\0-0} \\[5pt] &=&\pmatrix{3\\0\\0} \end{array}$

Für die Höhe $h$ einer Seitenfläche der Pyramide bezüglich der Kante, die in der $x_1x_2$ -Ebene liegt, ergibt sich also:

$\begin{array}[t]{rll} h&=&\left\vert\overrightarrow{MS}\right\vert \\[5pt] &=&\left\vert\pmatrix{0-3\\0-0\\4-0}\right\vert \\[5pt] &=&\sqrt{(-3)^2+0^2+4^2} \\[5pt] &=&5 \end{array}$

Damit beträgt der Flächeninhalt der vier Seitenflächen der Pyramide jeweils $\dfrac{1}{2}\cdot6\cdot5=15\;[\text{FE}].$

Zusammen mit dem Flächeninhalt der quadratischen Grundfläche von $6\cdot6=36\;[\text{FE}]$ folgt der Flächeninhalt $O_P$ der gesamten Oberfläche der Pyramide mit:

$O_P=36+4\cdot15=96\;[\text{FE}]$

Gleichung angeben

Einsetzen der Koordinaten der Eckpunkte der Pyramide in die Gleichungen ergibt, dass $B,D$ und $S$ in Ebene $(3)$ liegen. Da eine Ebene durch drei Punkte eindeutig festgelegt wird, teilt die Ebene $(3)$ folglich die Pyramide von oben betrachtet entlang der Diagonalen $\overline{BD}$ ihre Grundfläche und ist somit eine Symmetrieebene der Pyramide.

Gleichung begründen

Damit eine Ebene eine Symmetrieebene einer quadratischen Pyramide ist, muss sie durch die Spitze dieser verlaufen. Da die Koordinaten von $S$ Gleichung $(1)$ nicht erfüllen, kann diese keine Symmetrieebene der Pyramide beschreiben.

Richtungsvektoren bestimmen:

$\overrightarrow{CD}=\pmatrix{-3\\3\\0}-\pmatrix{3\\3\\0}=\pmatrix{-6\\0\\0}$

$\overrightarrow{CS}=\pmatrix{0\\0\\4}-\pmatrix{3\\3\\0}=\pmatrix{-3\\-3\\4}$

Ein möglicher Normalenvektor $\overrightarrow{n}$ der Ebene $E$ folgt also mit:

$\begin{array}[t]{rll} \overrightarrow{n}&=&\overrightarrow{CD}\times\overrightarrow{CS} \\[5pt] &=&\pmatrix{-6\\0\\0}\times\pmatrix{-3\\-3\\4} \\[5pt] &=&\pmatrix{0\cdot 4- 0\cdot (-3)\\0\cdot (-3)-((-6)\cdot4)\\(-6)\cdot(-3)-0\cdot (-3)} \\[5pt] &=&\pmatrix{0\\24\\18} \\[5pt] &=&6\cdot\pmatrix{0\\4\\3} \end{array}$

Mit dem gekürzten Normalenvektor folgt $E:4x_2+3x_3=d.$

Einsetzen der Koordinaten eines Punktes wie beispielsweise $C,$ der in der Ebene $CDS$ liegt, liefert für $d:$

$\begin{array}[t]{rll} 4\cdot3+3\cdot0&=&d \\[5pt] 12&=&d \end{array}$

Eine mögliche Gleichung der Ebene $E$ in Koordinatenform ist somit gegeben durch $4x_2+3x_3=12.$

Gleichung $\text{I}$ besagt, dass der Punkt $Q$ auf der Lotgeraden zu $E$ durch $P$ liegt.

Gleichung $\text{II}$ liefert, dass der Punkt $Q$ zudem in der Ebene $E$ liegt und damit der Schnittpunkt der Lotgerade mit $E$ ist.

Die Gleichung $\text{III}$ gibt den Abstand des Punktes $P$ zur Grundfläche der Pyramide, die in der Ebene $z=0$ liegt, an, welcher $p$ beträgt. Der Abstand von $P$ zu $E$ stimmt mit dem Abstand von $P$ zur Grundfläche überein.

Einsetzen der Koordinaten von $S$ in die Gleichung der Ebenenschar $E_k$ liefert:

$\begin{array}[t]{rll} 4 k \cdot 0+4 \sqrt{1-k^2} \cdot 0+3 \cdot 4&=&12 \\[5pt] 3\cdot4&=&12 \\[5pt] 12&=&12 \end{array}$

Somit ist der Punkt $S$ in allen Ebenen der Schar enthalten.

Ein Normalenvektor der Ebenenschar $E_k$ kann aus der Koordinatengleichung abgelesen werden und ergibt sich zu $\overrightarrow{n_k}=\pmatrix{4k\\4\sqrt{1-k^2}\\3}.$

Für den Schnittwinkel gilt also:

$\sin(\alpha)= \dfrac{3}{5}$

Rechenweg anzeigen

Somit hängt $\sin(\alpha),$ und damit auch die Größe des Schnittwinkels $\alpha,$ nicht von $k$ ab.

Die Ebene $E_{-1}$ verläuft laut Aufgabenstellung durch die Seitenfläche $ADS$ und somit parallel zur $x_2$ -Achse. Der Punkt $R_{-1}$ mit dem kürzesten Abstand zum Ursprung liegt also genau senkrecht zum Ursprung auf der $x_2$ -Achse und somit auf der $x_1$ -Achse.

$R_1$ liegt analog auf der anderen Seite des Ursprungs auf der $x_1$ -Achse.

Form beschreiben

Der Körper, der durch die Drehung der Fläche $OR_kS$ um die Strecke $\overline{OS}$ entsteht, ist ein Kegel mit der Spitze $S,$ der senkrecht zur in der $x_1x_2$ -Ebene liegenden Grundfläche halbiert wurde.

Volumen bestimmen

Die Höhe $h$ des Kegels ist durch die Pyramidenhöhe gegeben und beträgt somit $4\;\text{LE}.$

Da die Seiten der Grundfläche der Pyramide $6\;\text{LE}$ lang sind, folgt für den Flächeninhalt der kreisförmigen Grundfläche $G$ mit Radius $r=3:$

$G=\pi\cdot3^2=9\pi\;[\text{FE}]$

Insgesamt ergibt sich damit folgendes Volumen $V$ des halben Kegels:

$V=\dfrac{1}{2}\cdot\left(\dfrac{1}{3}\cdot9\pi \cdot 4\right)=6\pi\;[\text{VE}]$

Lösung II 2

Zwei Geraden sind genau dann orthogonal zueinander, wenn das Produkt ihrer Richtungsvektoren Null ergibt.

Mit den Richtungsvektoren $r_4=\pmatrix{4\\1\\4-2}=\pmatrix{4\\1\\2}$ und $r_{0,5}=\pmatrix{0,5\\1\\0,5-2}=\pmatrix{0,5\\1\\-1,5}$ folgt:

$\pmatrix{4\\1\\2}\circ \pmatrix{0,5\\1\\-1,5}=0$

Rechenweg anzeigen

Die Gerade $g_4$ ist somit orthogonal zur Gerade $g_{0,5}.$

Aus der Ebenengleichung kann ein Normalenvektor von $E$ mit $n_E=\pmatrix{3\\-6\\2}$ abgelesen werden.

Für den Winkel folgt:

$\alpha \approx 18,2^\circ$

Rechenweg anzeigen

Enthält eine Gerade der Schar den Ursprung, dann müsste gelten:

$g_a: \pmatrix{0\\0\\0}=\pmatrix{1\\2\\5}+t\cdot \pmatrix{a\\1\\a-2}$

Aus der zweiten Zeile folgt direkt:

$\begin{array}[t]{rll} 0&=& 2+t\cdot 1&\quad \scriptsize \mid\; -2\\[5pt] -2&=& t \end{array}$

Einsetzen von $t=-2$ in die erste Zeile ergibt:

$\begin{array}[t]{rll} 0&=& 1+(-2)\cdot a&\quad \scriptsize \mid\; -1\\[5pt] -1&=& -2a&\quad \scriptsize \mid\; :(-2)\\[5pt] 0,5&=& a \end{array}$

Probe mit der dritten Zeile liefert:

$\begin{array}[t]{rll} 0&=& 5+(-2)\cdot (0,5-2)& \\[5pt] 0&=& 5+3& \\[5pt] 0&=& 8 \end{array}$

Da die Werte von $t$ und $a$ in der dritten Zeile zu einem Widerspruch führen, enthält keine Gerade der Schar den Ursprung.

Spannvektoren der Ebene sind alle Richtungsvektoren der Geradenschar $g_a$ und somit beispielsweise $r_0=\pmatrix{0 \\1\\-2}$ und $r_2=\pmatrix{2 \\1\\0}.$

Ein Normalenvektor der Ebene $F$ ergibt sich mit dem Kreuzprodukt der Spannvektoren:

$\begin{array}[t]{rll} \overrightarrow{n_F}&=& \pmatrix{0 \\1\\-2} \times \pmatrix{2 \\1\\0} & \\[5pt] &=& \pmatrix{1\cdot 0-(-2)\cdot 1\\(-2)\cdot 2-0\cdot 0\\0\cdot 1-1\cdot 2} & \\[5pt] &=& \pmatrix{2 \\-4\\-2} & \\[5pt] &=& 2\cdot \pmatrix{1 \\-2\\-1} \end{array}$

Einsetzen des gekürzten Normalenvektors in die allgemeine Koordinatenform ergibt:

$F: \quad 1x_1-2x_2-1x_3=d$

Punktprobe mit dem Stützpunkt der Geradenschar:

$\begin{array}[t]{rll} F: \quad 1\cdot 1-2\cdot 2-1\cdot 5&=& d & \\[5pt] -8 &=& d \end{array}$

Eine Koordinatengleichung von $F$ ist somit gegeben durch $F: \; x_1-2x_2-x_3=-8.$

Die Punkte liegen alle auf der folgenden Gerade:

$\begin{array}[t]{rll} p: \; \overrightarrow{x}&=& \pmatrix{1+r\\2-2r\\5-r}&\\[5pt] &=& \pmatrix{1\\2\\5}+r\cdot \pmatrix{1\\-2\\-1} \end{array}$

Der Richtungsvektor der Geraden, auf der die Punkte $P_r$ liegen, entspricht dem Normalenvektor von $F.$

Die Gerade verläuft folglich orthogonal zu $F.$

Alle Geraden $g_a$ liegen in $F$ und enthalten den Punkt $Q(1\mid 2\mid 5).$

Da die Gerade $p$ durch die Punkte $P_r$ ebenfalls den Punkt $Q$ enthält und orthogonal zu $F$ ist, gilt:

$\begin{array}[t]{rll} d(P_r;g_a)&=& d(P_r;Q)&\\[5pt] &=& r\cdot \left| \pmatrix{1\\-2\\-1} \right|&\\[5pt] &=& r\cdot \sqrt{1^2+(-2)^2+(-1)^2} &\\[5pt] &=& r\cdot \sqrt{6} \end{array}$

Die Aussage ist somit korrekt.

Die Gerade $k$ liegt genau dann in der Ebene $F,$ wenn sie einen gemeinsamen Punkt mit der Ebene besitzt und ihr Richtungsvektor orthogonal zum Normalenvektor der Ebene ist.

Ein gemeinsamer Punkt ist der Stützpunkt der Geraden mit dem Ortsvektor $\overrightarrow{OS}=\pmatrix{1\\2\\5}.$

Für den Richtungsvektor gilt:

$\begin{array}[t]{rll} \overrightarrow{r_k}\circ \overrightarrow{n_F}&=& \pmatrix{1\\0\\1} \circ \pmatrix{1\\-2\\-1}&\\[5pt] &=& 1\cdot 1+0\cdot (-2)+1\cdot (-1)&\\[5pt] &=& 0 \end{array}$

Somit verläuft die Gerade $k$ orthogonal zum Normalenvektor der Ebene $F$ und liegt folglich in dieser.

Da die $x_2$ -Koordinate des Richtungsvektors von $k$ 0 ist, während alle Geraden der Schar die $x_2$ -Koordinate 1 besitzen, gehört $k$ nicht zur Schar.

Da alle Geraden $g_a$ in $F$ liegen, ist die Gerade $h$ die Schnittgerade von $F$ mit der $x_1x_2$ -Ebene.

Da $k$ in $F$ liegt und mit jeder Gerade $g_a$ nur den Punkt $P(1\mid 2\mid 5)$ gemeinsam hat, liegt der Schnittpunkt $S$ von $k$ mit der $x_1 x_2$ -Ebene auf keiner Gerade $g_a$ und ist somit der gesuchte Punkt.

Für diesen Schnittpunkt gilt:

$k: \; \pmatrix{x_1\\x_2\\0}=\pmatrix{1\\2\\5}+s\cdot \pmatrix{1\\0\\1}$

Aus der letzten Zeile folgt direkt:

$\begin{array}[t]{rll} 0&=& 5+s\cdot 1&\quad \scriptsize \mid\; -5 \\[5pt] -5&=& s \end{array}$

Einsetzen von $s=-5$ in die Geradengleichung liefert:

$\begin{array}[t]{rll} k: \; \overrightarrow{OS}&=& \pmatrix{1\\2\\5}-5\cdot \pmatrix{1\\0\\1}& \\[5pt] &=& \pmatrix{-4\\2\\0} \end{array}$

Die Koordinaten des gesuchten Punkts sind somit gegeben durch $S(-4 \mid 2\mid 0).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?