Wahlteil B1

Aufgabe B1.1

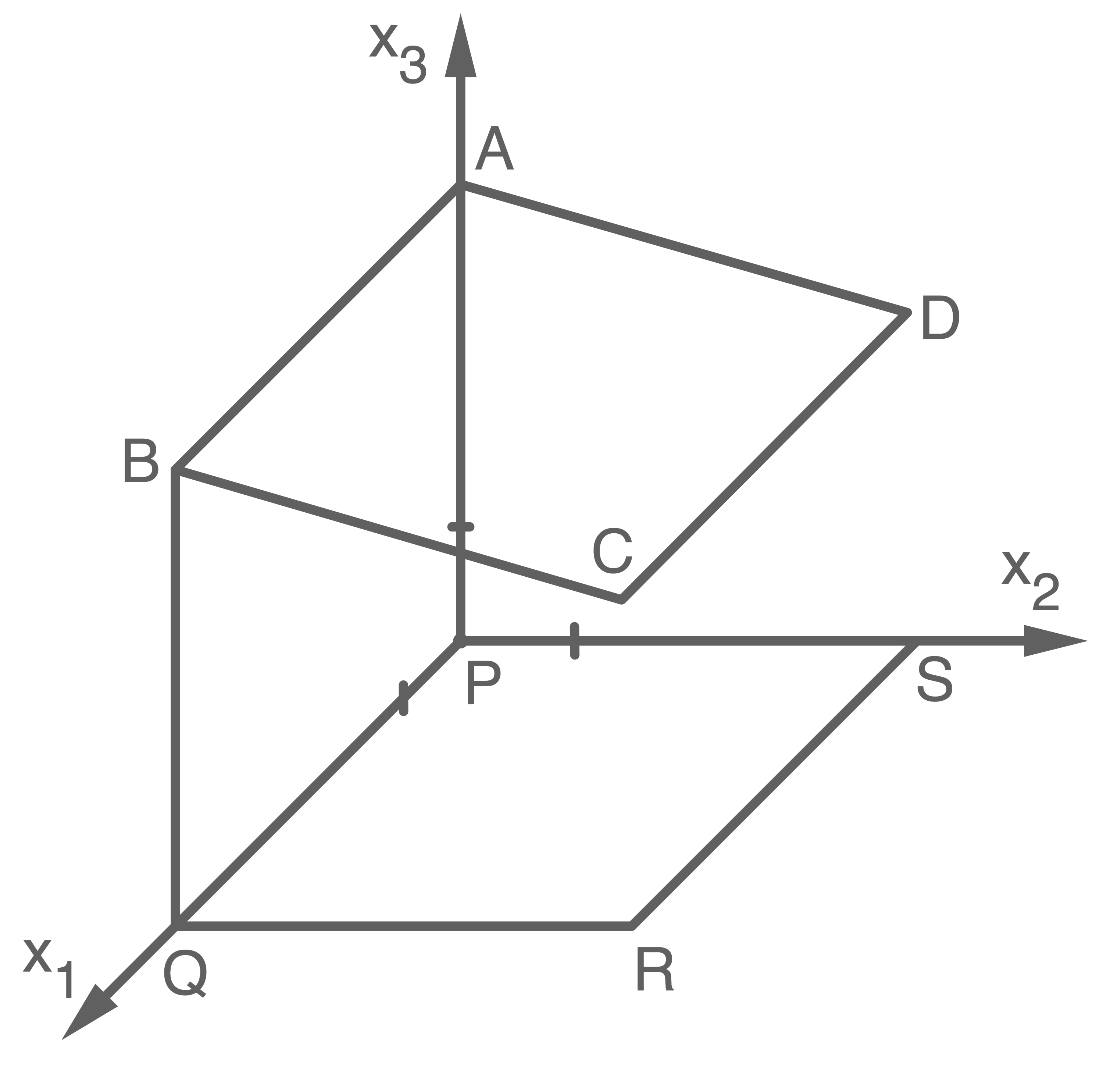
Über einer Terrasse ist als Sonnenschutz eine Markise an einer Hauswand befestigt.
In einem Koordinatensystem stellen die Punkte $P(0\mid 0\mid 0)$ , $Q(5\mid 0\mid 0)$ , $R(5\mid 4\mid 0)$ , $S(0\mid 4\mid 0)$ die Eckpunkte der Terrasse dar. Die Markise wird durch das Rechteck mit den Eckpunkten $A(0\mid 0\mid 4)$ , $B(5\mid 0\mid 4)$ , $C(5\mid 3,9\mid 2,7)$ , $D(0\mid 3,9\mid 2,7)$ beschrieben (alle Koordinatenangaben in Meter).
Die Lage der Hauswand wird durch die $x_1x_3$ -Ebene beschrieben.

3D-Koordinatensystem mit Punkten A, B, C, D, P, Q, R und S, dargestellt in einem kubischen Format.

Bestimme eine Koordinatengleichung der Ebene, welche die Lage der Markise beschreibt.
Berechne den Winkel zwischen Markise und Hauswand.

(3 VP)

In der Mitte zwischen $Q$ und $R$ steht eine $30\,\text{cm}$ hohe Stablampe. Am Markisenrand $CD$ wird ein senkrecht nach unten hängender Regenschutz angebracht, der genau bis auf die Terrasse reicht. Bei starkem Wind schwingt er frei um $CD.$

Kann der Regenschutz dabei die Stablampe berühren?

Welchen Abstand von der Hauswand darf die Stablampe auf der Terrasse höchstens haben, damit dies nicht passiert?

(4 VP)

Die Sonne scheint und der Regenschutz wird entfernt. Die Richtung der Sonnenstrahlen

wird durch den Vektor $\vec{v} = \begin{pmatrix}1\\-1\\-3\end{pmatrix}$ beschrieben.

Begründe ohne Rechnung, dass die Terrasse nicht vollständig beschattet wird.
Die Markise kann ein- und ausgefahren werden. Dabei bewegen sich die äußeren Eckpunkte der Markise längs der Geraden $BC$ und $AD$ . Die Markise wird nun so weit eingefahren, dass der Terrassenrand zwischen $Q$ und $R$ genau zur Hälfte im Schatten liegt.
Bestimme die neuen Koordinaten der äußeren Eckpunkte der Markise.

(4 VP)

Aufgabe B1.2

Ein Großhändler gibt an, dass sein Weizensaatgut einen Keimfähigkeit von mindestens 80% hat. Mehrere Kunden vermuten, dass die Keimfähigkeit in Wirklichkeit kleiner ist.
Deswegen wird die Aussage des Großhändlers mit Hilfe eines Tests auf einem Signifikantsniveau von 10% überprüft, indem 500 Weizenkörner untersucht werden.
Als Nullhypothese wird die Angabe des Großhändlers verwendet.

Formuliere die zugehörige Entscheidungsregel in Worten.

Die tatsächliche Keimfähigkeit des Saatguts beträgt 82%.
Wie groß ist in einem Fall die Wahrscheinlichkeit dafür, dass bei obigem Test die Nullhypothese fälschlicherweise verworfen wird?

(4 VP)

Aufgabe 1.1

$\blacktriangleright$ Bestimmen einer Koordinatengleichung für Ebene

Der Aufgabenstellung kannst du entnehmen, dass das Rechteck $ABCD$ die Markise darstellen soll. Du sollst nun eine Koordinatengleichung der Ebene $E$ aufstellen, in der dieses Rechteck liegt.
Eine Ebenengleichung in Koordinatenform sieht im allgemeinen folgendermaßen aus:

$E: n_1\cdot x_1 +n_2\cdot x_2 +n_3\cdot x_3 = a$

Dabei ist $\overrightarrow{n} = \begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}$ ein Normalenvektor zur Ebene $E$ , also ein Vektor, der senkrecht auf der Ebene steht. Ein solcher Normalenvektor ergibt sich aus dem Kreuzprodukt zweier Vektoren, die in der Ebene liegen. Der Parameter $a$ kann über eine Punktprobe bestimmt werden.
Gehe also wie folgt vor:

Berechne einen Normalenvektor von $E$ mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte $A$ , $B$ , $C$ , $D$

Führe eine Punktprobe durch um $a$ zu bestimmen

Stelle die Ebenengleichung auf

1. Schritt: Bestimmen des Normalenvektors

Zwei Vektoren, die in $E$ liegen erhältst du zum Beispiel mit den Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ :

$\overrightarrow{AB} = \overrightarrow{OB}- \overrightarrow{OA} =\begin{pmatrix}5\\0\\0\end{pmatrix}$
$\overrightarrow{AD} = \overrightarrow{OD}- \overrightarrow{OA} =\begin{pmatrix}0\\3,9\\-1,3\end{pmatrix}$

Berechne nun $\overrightarrow{n}$ mit Hilfe des Kreuzprodukts:

$\begin{array}[t]{rll} \overrightarrow{n}&=&\overrightarrow{AB}\times \overrightarrow{AD} \\[5pt] &=&\begin{pmatrix}5\\0\\0\end{pmatrix}\times\begin{pmatrix}0\\3,9\\-1,3\end{pmatrix} \\[5pt] &=&\begin{pmatrix}0\\6,5\\19,5\end{pmatrix} \\[5pt] \end{array}$

2. Schritt: Punktprobe

Nun lautet die bisherige Ebenengleichung $E: 0\cdot x_1 + 6,5\cdot x_2 +19,5\cdot x_3 = a$
Setze dort nun die Koordinaten eines Punktes der Ebene ein und berechne so $a$ . Wähle dazu beispielsweise $C(5\mid 3,9 \mid 2,7)$ :

$a = 0 \cdot 5 + 6,5\cdot 3,9 + 19,5\cdot 2,7 = 78$

3. Schritt: Ebenengleichung aufstellen

Die Ebenengleichung in Koordinatenform lautet nun :

$E: 6,5\cdot x_2 +19,5\cdot x_3 = 78$

$\blacktriangleright$ Bestimmen des Winkels zwischen Markise und Hauswand

Da das Rechteck, das die Markise darstellt in der Ebene $E$ liegt und die Lage der Hauswand durch die $x_1x_3$ -Ebene beschrieben wird, ist hier der Schnittwinkel $\alpha$ dieser beiden Ebenen gesucht. Einen Schnittwinkel zwischen zwei Ebenen berechnet man allgemein über den Schnittwinkel der zugehörigen Normalenvektoren $\overrightarrow{n}$ und $\overrightarrow{m}$ .

Einen Normalenvektor von $E$ hast du bereits im vorherigen Aufgabenteil berechnet mit $\overrightarrow{n} = \begin{pmatrix}0\\6,5\\19,5\end{pmatrix}$ . Ein Normalenvektor der $x_1x_3$ -Ebene ist $\overrightarrow{m} = \begin{pmatrix}0\\1\\0\end{pmatrix}$ . Damit ergibt sich nun der Schnittwinkel wie folgt:

$\cos(\alpha) = \dfrac{\left| \overrightarrow{n} \cdot \overrightarrow{m}\right|}{\left|\overrightarrow{n} \right| \cdot \left|\overrightarrow{m} \right|}$

Vollständige Lösung anzeigen

Der Winkel zwischen der Markise und der Hauswand beträgt ca. $71,6\,^{\circ}$ .

$\blacktriangleright$ Entscheiden, ob der Regenschutz die Stablampe berühren kann

Fertige dir für diesen Aufgabenteil zunächst eine Skizze an. Anhand der Koordinaten der Punkte $Q$ , $R$ $C$ und $B$ kannst du erkennen, dass diese alle in einer Ebene liegen. Der Vektor $\overrightarrow{DC} = \begin{pmatrix}5\\0\\0\end{pmatrix}$ , der die Kante der Markise beschreibt, um die der Regenschutz rotiert liegt senkrecht dazu, da er parallel zur $x_1$ -Achse verläuft. Es reicht also aus das ganze Gebilde von vorne zu betrachten und die Rotation des Regenschutzes durch einen Kreis zu beschreiben. Damit ergibt sich folgende Skizze:

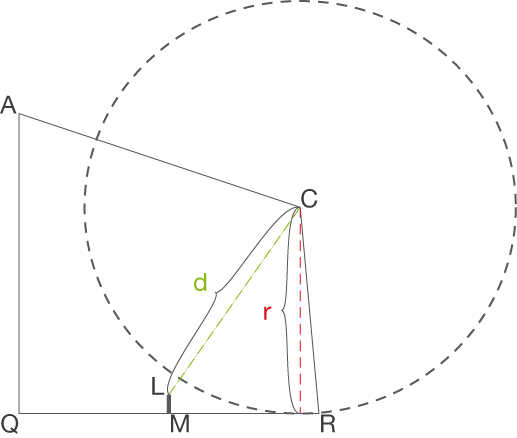
Diagramm mit Linien und Kurven, das verschiedene geometrische Konzepte darstellt.

In der Skizze bezeichnet $r$ die Länge des Regenschutzes und $d$ den Abstand zwischen dem Punkt $C$ und dem Endpunkt $L$ der Lampe. Der Regenschutz kann die Lampe nur dann treffen, wenn der Kreis die Linie, die die Lampe darstellt, schneidet. Du kannst also erkennen, dass der Regenschutz die Lampe dann trifft, wenn der Regenschutz länger ist, als der Abstand zwischen $C$ und $L$ . Überprüfe also, ob $r \lt d$ gilt, gehe dazu wie folgt vor:

Berechne die Länge $r$ des Regenschutzes, die dem Abstand von $C$ zur Terrasse entspricht

Berechne die Koordinaten des Lampenendpunktes $L$

Berechne den Abstand $d$ zwischen $L$ und $C$ über den Betrag des Verbindungsvektors

Vergleiche

1. Schritt: Länge des Regenschutzes bestimmen

Der Regenschutz hängt senkrecht hinunter auf die Terrasse, $r$ entspricht also dem Abstand von $C$ zur Terrasse. Da die Terrasse in der $x_1x_2$ -Ebene liegt, entspricht $r$ genau der $x_3$ -Koordinate von $C$ . Insgesamt ergibt sich also:

$\Rightarrow r = 2,7 \,$ m

2. Schritt: Koordinaten von $L$ bestimmen

Die Koordinaten des Entpunktes der Lampe kannst du dir „zusammenbasteln“. Berechne dazu zuerst die Koordinaten des Mittelpunktes $M$ der Strecke $\overline{QR}$ . Da die Lampe senkrecht nach oben steht, ergeben sich die Koordinaten von $L$ dann, indem du die $x_3$ -Koordinate um $30$ cm, also $0,3$ m erhöhst. Da sich bei den Punkten $Q$ und $R$ nur die $x_2$ -Koordinate unterscheidet, erhältst du den Mittelpunkt, indem du die Hälfte der Differenz der $x_2$ -Koordinaten auf die $x_2$ -Koordinate von $Q$ addierst.
Insgesamt ergibt sich so:

$M(5\mid\, 2\mid\, 0) \quad L(5\mid\,2\mid\,0,3)$

3. Schritt: Abstand berechnen

Der Abstand zwischen $L$ und $C$ berechnet sich wie folgt:

$\begin{array}[t]{rll} d &=&\left|\overrightarrow{LC} \right| \quad \scriptsize \\[5pt] &=&\left|\begin{pmatrix}5\\3,9\\2,7\end{pmatrix} - \begin{pmatrix}5\\2\\0,3\end{pmatrix} \right| \quad \scriptsize \\[5pt] &=& \left|\begin{pmatrix}0\\1,9\\2,4\end{pmatrix}\right| \quad \scriptsize \\[5pt] &=&\sqrt{0^2+1,9^2+2,4^2} \quad \scriptsize \\[5pt] &=& \sqrt{9,37} \quad \scriptsize \\[5pt] &\approx& 3,06 \quad \scriptsize \\ \end{array}$

4. Schritt: Vergleichen

Es gilt: $r \lt d$ . Daher ist der Regenschutz kürzer als der Abstand von $C$ zum Ende der Lampe. Insgesamt folgt also:

Der Regenschutz kann die Lampe nicht berühren.

$\blacktriangleright$ Maximalen Abstand berechnen

Eben hast du überprüft, ob die Lampe weit genug entfernt ist. Nun sollst du den maximalen Abstand der Lampe von der Hauswand berechnen, sodass die Lampe gerade so den Regenschutz nicht berühren kann, stelle dir also vor die Lampe würde entlang der Strecke $\overline{QR}$ verschoben werden. Dabei ändern sich die $x_1$ - und $x_3$ -Koordinate der Lampenpunkte nicht. Nur die $x_2$ -Koordinate ändert sich und gibt genau den Abstand der Lampe von der Hauswand an. Finde also die größtmögliche $x_2$ -Koordinate von $L$ und $M$ sodass gerade noch gilt

$r \lt d$ .

Du kannst wie folgt vorgehen:

Bestimme eine Formel für den Abstand $d(t)$ zwischen $C$ und $L$ in Abhängigkeit von der $x_2$ -Koordinate $t$ von $L$

Löse $d(t) = r$

1. Schritt: Formel aufstellen

Oben hast du gesehen, dass sich der Abstand zwischen $C$ und $L$ über den Vektorbetrag $\left| \overrightarrow{LC}\right|$ berechnet. Hier hat der Punkt $L$ allerdings die Koordinaten $L_t(5\mid\,t\mid0,3)$ . Setze also diese Koordinaten in Abhängigkeit von $t$ in die Abstandsberechnung ein:

$\begin{array}[t]{rll} d(t) &=&\left|\overrightarrow{L_tC} \right| \quad \scriptsize \\[5pt] &=&\left|\begin{pmatrix}5\\3,9\\2,7\end{pmatrix} - \begin{pmatrix}5\\t\\0,3\end{pmatrix} \right| \quad \scriptsize \\[5pt] &=& \left|\begin{pmatrix}0\\3,9-t\\2,4\end{pmatrix}\right| \quad \scriptsize \\[5pt] &=&\sqrt{(3,9-t)^2+2,4^2} \quad \scriptsize \\ \end{array}$

2. Schritt: Gleichung lösen

Es ergibt sich die Gleichung $\sqrt{(3,9-t)^2+2,4^2} =$ $2,7 \Leftrightarrow \sqrt{(3,9-t)^2+2,4^2}-2,7 = 0$ . Diese kannst du mit deinem GTR lösen, indem du im Graph-Menü den Graphen von $f(x)= \sqrt{(3,9-t)^2+2,4^2}-2,7$ zeichnen lässt und die Nullstellen wie folgt bestimmst:

2ND $\rightarrow$ TRACE(CALC) $\rightarrow$ 2: zero

Du erhältst dann die Lösung: $t \approx 2,663$ .

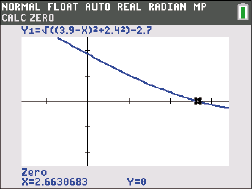
Grafik einer mathematischen Funktion mit einer Kurve und Koordinatenachsen.

Die Lampe darf höchstens $2,66$ m von der Wand entfernt stehen, um nicht vom Regenschutz getroffen zu werden.

$\blacktriangleright$ Schattenfall begründen

Der Vektor $\overrightarrow{v} = \begin{pmatrix}1\\-1\\-3\end{pmatrix}$ beschreibt die Richtung der Sonnenstrahlen. Der Schatten entsteht durch Verschiebung des Rechtecks $ABCD$ in Richtung dieses Vektors. Setzt du diesen Vektor beispielsweise an den Punkt $D$ , so erhältst du einen Eckpunkt des Schattens, den Schattenpunkt von $D$ . Da $\overrightarrow{v}$ eine positive $x_1$ -Koordinate und eine negative $x_2$ -Koordinate und dazu auch noch eine negative $x_3$ -Koordinate hat, liegt der Schattenpunkt von $D$ unterhalb der Markise auf der Terrasse. Die Hauswand wirft bei dieser Richtung keinen Schatten in Richtung der Terrasse. Da eine Ecke des Schattens auf jeden Fall innerhalb der Terrassenfläche liegt, muss auch ein Teil der besonnten Fläche auf der Terrasse liegen. Daher ist die Terrasse so nicht vollständig beschattet.

$\blacktriangleright$ Koordinaten der Eckpunkte bestimmen

Du kannst hierzu wie folgt vorgehen:

Berechne die Koordinaten des Punktes $M‘$ , dessen Schatten auf den Mittelpunkt $M$ der Strecke $\overline{QR}$ fällt. Konstruiere dazu eine Gerade, auf der $M$ liegt und die in Richtung der Sonnenstrahlen verläuft. Der gesuchte Punkt ist dann der Schnittpunkt mit der Ebene $E$ , in der die Markise liegt

Die gesuchten neuen Eckpunkte erhältst du dann durch anpassen der $x_1$ -Koordinate, da alle Punkte des neuen Randes der Markise die gleichen $x_2$ und $x_3$ -Koordinaten besitzen

1. Schritt: Schnittpunkt bestimmen

Stelle zuerst die Gerade auf, die $M‘$ und $M$ verbinden soll. Dazu benötigst du einen Richtungsvektor und den Ortsvektor eines Punktes auf der Geraden. Hierfür kannst du den Richtungsvektor der Sonnenstrahlen und den Punkt $M$ verwenden. Damit ergibt sich die gesuchte Geradengleichung wie folgt:

$g: \overrightarrow{x} = \overrightarrow{OM} + t \cdot \overrightarrow{v} = \begin{pmatrix}5\\2\\0\end{pmatrix} + t \cdot \begin{pmatrix}1\\-1\\-3\end{pmatrix}$

Für die Punkte auf der Geraden $g$ ergeben sich damit die folgenden Koordinaten:

$x_1 = 5+t$ , $x_2 = 2-t$ und $x_3 = 0 -3t$

Setzt du dies nun in die Ebenengleichung von $E$ ein, so erhältst du folgende Gleichung:

$\begin{array}[t]{rll} 78&=&6,5\cdot x_2 + 19,5\cdot x_3 \quad \scriptsize \\[5pt] 78 &=&6,5\cdot (2-t)+ 19,5\cdot(-3t) \quad \scriptsize \\[5pt] &=& 13-6,5t-58,5t\quad \scriptsize \\[5pt] &=&13-65t \quad \scriptsize \mid\;-13 \\[5pt] 65&=&-65t \quad \scriptsize \mid\;:(-65) \\[5pt] -1&=&t \quad \scriptsize \\ \end{array}$

Eingesetzt in $g$ ergibt sich damit dann der Ortsvektor von $M‘$ :

$\begin{array}[t]{rll} \overrightarrow{OM‘}&=& \begin{pmatrix}5\\2\\0\end{pmatrix} + t \cdot \begin{pmatrix}1\\-1\\-3\end{pmatrix} \quad \scriptsize \\[5pt] &=& \begin{pmatrix}5\\2\\0\end{pmatrix} -1 \cdot \begin{pmatrix}1\\-1\\-3\end{pmatrix} \quad \scriptsize \\[5pt] &=&\begin{pmatrix}4\\3\\3\end{pmatrix} \quad \scriptsize \\ \end{array}$

Der Punkt $M‘(4\mid\,3\mid\,3)$ liegt jetzt auf der Strecke zwischen den neuen Eckpunkten der Markise $C‘$ und $D‘$ . Du musst jetzt noch die $x_1$ -Koordinate durch die $x_1$ -Koordinaten von $C$ und $D$ ersetzen. Damit ergeben sich die neuen Eckpunkte wie folgt:

$C‘(5\mid\, 3\mid\, 3)$ und $D‘(0\mid\, 3\mid,3 )$

Aufgabe 1.2

$\blacktriangleright$ Entscheidungsregel formulieren

Du sollst hier eine Entscheidungsregel formulieren, das heißt eine Regel dafür formulieren, für welche Stichprobenwerte die Behauptung des Großhändlers verworfen werden kann und für welche Stichprobenwerte diese nicht verworfen werden kann. Dabei ist vorgegeben, dass die Angabe des Großhändlers als Nullhypothese verwendet wird. Es gilt also:

$H_0: p \geq 0,8$ und $H_1: p \lt 0,8$

Es wird also ein linksseitiger Hypothesentest auf dem Signifikanzniveau $\alpha = 0,1$ durchgeführt.

Wir betrachten hier die Zufallsvariable $X$ , die die Anzahl der gekeimten Weizenkörner beschreibt. Diese kann unter der Angabe des Großhändlers als binomialverteilt mit den Parameter $n =500$ und $p = 0,8$ angenommen werden, da jedes Weizenkorn unabhängig von den übrigen Körnern mit gleicher Wahrscheinlichkeit keimt und jeweils nur „keimt“ und „keimt nicht“ betrachtet werden. Da ein linksseitiger Hypothesentest durchgeführt wird, wird die Nullhypothese nur für kleine Werte abgelehnt.
Der Ablehnungsbereich hat daher die Form

$\overline{K} = [0,k]$

Du musst nun also die Grenze $k$ des Ablehnungsbereichs bestimmen um sagen zu können, für welche Werte die Nullhypothese verworfen werden kann. Hierfür musst du das Signifikanzniveau nutzen. Dies gibt die Irrtumswahrscheinlichkeit an, also genau die Wahrscheinlichkeit dafür, dass die Nullhypothese gilt und die Stichprobe trotzdem einen Wert aus dem Ablehnungsbereich liefert. Es ist also das größte $k$ gesucht, welches gerade noch folgende Ungleichung erfüllt:

$P(X\leq k) \leq 0,1$

Dazu kannst du den BinomCdf-Befehl deines GTR verwenden. Gib die Funktion $f(x)= P(X\leq x)$ im $Y=$ -Menü des GTR über den BinomCdf-Befehl ein. Diesen findest du unter

2ND $\rightarrow$ VARS(DISTR) $\rightarrow$ B: BinomCdf

In die Klammern musst du dann die Parameter eingeben: $n= 500$ , $p = 0,8$ und $k =x$ . Anschließend kannst du dir mit dem folgenden Befehl die Wertetabelle anzeigen lassen.

2ND GRAPH(TABLE)

Wähle dann aus dieser Tabelle das größte $x$ , sodass $y$ gerade noch kleiner oder gleich $0,1$ ist. Du findest folgende Werte: $P(X\leq 387)\approx 0,08261$ und $P(X\leq 388) \approx 0,10044$

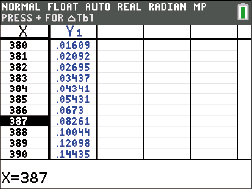
Tabelle mit X- und Y-Werten, angezeigt auf einem Taschenrechner-Display.

Damit ist das gesuchte $k = 387$ und die Entscheidungsregel lässt sich wie folgt formulieren:

Werden höchstens $387$ Weizenkörner gefunden, die keimen, so wird die Nullhypothese, also die Behauptung des Großhändlers auf dem Signifikanznieveau $\alpha = 0,1$ verworfen und den zweifelnden Kunden rechtgegeben. Werden aber mehr als $387$ keimende Weizenkörner gefunden, so kann die Behauptung des Großhändlers auf dem Signifikanzniveau $\alpha$ nicht verworfen werden.

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Gesucht ist die Wahrscheinlichkeit dafür, dass die Nullhypothese verworfen wird, obwohl die Wahrscheinlichkeit $p = 0,82$ gilt. Oben hast du berechnet, dass die Nullhypothese dann abgelehnt wird, wenn höchstens $387$ Weizenkörner keimen. Definiere eine Zufallsvariable $Y$ , die die zufällige Anzahl gekeimter Weizenkörner beschreibt und dabei unter der vorgegebenen tatsächlichen Wahrscheinlichkeit $p=0,82$ verteilt ist.
Gesucht ist dann die Wahrscheinlichkeit $P(Y\leq 387)$ .

$Y$ ist binomialverteilt mit den Parametern $n =500$ und $p =0 ,82$ . Berechne nun die gesuchte Wahrscheinlichkeit mit dem BinomCdf-Befehl deines GTR:

$P(Y \leq 387)\approx 0,005 = 0,5\,\%$

Die Wahrscheinlichkeit dafür, bei einer tatsächlichen Keimfähigkeit von $82\,\%$ die Nullhypothese zu verwerfen beträgt ca. $0,5\,\%$ .

Aufgabe 1.1

$\blacktriangleright$ Bestimmen einer Koordinatengleichung für Ebene

$E: n_1\cdot x_1 +n_2\cdot x_2 +n_3\cdot x_3 = a$

Berechne einen Normalenvektor von $E$ mit Hilfe des Kreuzprodukts zweier Verbindungsvektoren der Punkte $A$ , $B$ , $C$ , $D$

Führe eine Punktprobe durch um $a$ zu bestimmen

Stelle die Ebenengleichung auf

1. Schritt: Bestimmen des Normalenvektors

Zwei Vektoren, die in $E$ liegen erhältst du zum Beispiel mit den Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ :

Berechne nun $\overrightarrow{n}$ mit Hilfe des Kreuzprodukts:

2. Schritt: Punktprobe

$a = 0 \cdot 5 + 6,5\cdot 3,9 + 19,5\cdot 2,7 = 78$

3. Schritt: Ebenengleichung aufstellen

Die Ebenengleichung in Koordinatenform lautet nun :

$E: 6,5\cdot x_2 +19,5\cdot x_3 = 78$

$\blacktriangleright$ Bestimmen des Winkels zwischen Markise und Hauswand

$\cos(\alpha)=\dfrac{\left| \overrightarrow{n} \cdot \overrightarrow{m}\right|}{\left|\overrightarrow{n} \right| \cdot \left|\overrightarrow{m} \right|}$

Vollständige Lösung anzeigen

Der Winkel zwischen der Markise und der Hauswand beträgt ca. $71,6\,^{\circ}$ .

$\blacktriangleright$ Entscheiden, ob der Regenschutz die Stablampe berühren kann

Berechne die Länge $r$ des Regenschutzes, die dem Abstand von $C$ zur Terrasse entspricht

Berechne die Koordinaten des Lampenendpunktes $L$

Berechne den Abstand $d$ zwischen $L$ und $C$ über den Betrag des Verbindungsvektors

Vergleiche

1. Schritt: Länge des Regenschutzes bestimmen

$\Rightarrow r = 2,7 \,$ m

2. Schritt: Koordinaten von $L$ bestimmen

$M(5\mid\, 2\mid\, 0) \quad L(5\mid\,2\mid\,0,3)$

3. Schritt: Abstand berechnen

Der Abstand zwischen $L$ und $C$ berechnet sich wie folgt:

4. Schritt: Vergleichen

Es gilt: $r \lt d$ . Daher ist der Regenschutz kürzer als der Abstand von $C$ zum Ende der Lampe. Insgesamt folgt also:

Der Regenschutz kann die Lampe nicht berühren.

$\blacktriangleright$ Maximalen Abstand berechnen

$r \lt d$ .

Du kannst wie folgt vorgehen:

Bestimme eine Formel für den Abstand $d(t)$ zwischen $C$ und $L$ in Abhängigkeit von der $x_2$ -Koordinate $t$ von $L$

Löse $d(t) = r$

1. Schritt: Formel aufstellen

2. Schritt: Gleichung lösen

Shift $\rightarrow$ F5: G-Solv $\rightarrow$ F1: Root

Du erhältst dann die Lösung: $t \approx 2,663$ .

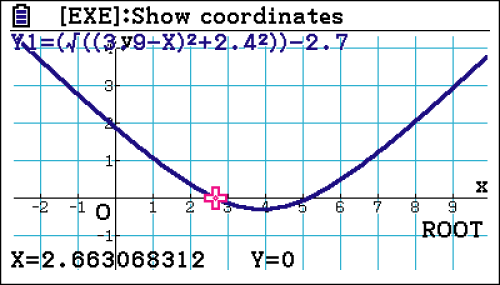
Grafische Darstellung einer mathematischen Funktion mit Koordinaten und einem hervorgehobenen Punkt.

Die Lampe darf höchstens $2,66$ m von der Wand entfernt stehen, um nicht vom Regenschutz getroffen zu werden.

$\blacktriangleright$ Schattenfall begründen

$\blacktriangleright$ Koordinaten der Eckpunkte bestimmen

Du kannst hierzu wie folgt vorgehen:

Berechne die Koordinaten des Punktes $M‘$ , dessen Schatten auf den Mittelpunkt $M$ der Strecke $\overline{QR}$ fällt. Konstruiere dazu eine Gerade, auf der $M$ liegt und die in Richtung der Sonnenstrahlen verläuft. Der gesuchte Punkt ist dann der Schnittpunkt mit der Ebene $E$ , in der die Markise liegt

Die gesuchten neuen Eckpunkte erhältst du dann durch anpassen der $x_1$ -Koordinate, da alle Punkte des neuen Randes der Markise die gleichen $x_2$ und $x_3$ -Koordinaten besitzen

1. Schritt: Schnittpunkt bestimmen

$g: \overrightarrow{x} = \overrightarrow{OM} + t \cdot \overrightarrow{v} = \begin{pmatrix}5\\2\\0\end{pmatrix} + t \cdot \begin{pmatrix}1\\-1\\-3\end{pmatrix}$

Für die Punkte auf der Geraden $g$ ergeben sich damit die folgenden Koordinaten:

$x_1 = 5+t$ , $x_2 = 2-t$ und $x_3 = 0 -3t$

Setzt du dies nun in die Ebenengleichung von $E$ ein, so erhältst du folgende Gleichung:

Eingesetzt in $g$ ergibt sich damit dann der Ortsvektor von $M‘$ :

$C‘(5\mid\, 3\mid\, 3)$ und $D‘(0\mid\, 3\mid,3 )$

Aufgabe 1.2

$\blacktriangleright$ Entscheidungsregel formulieren

$H_0: p \geq 0,8$ und $H_1: p \lt 0,8$

Es wird also ein linksseitiger Hypothesentest auf dem Signifikanzniveau $\alpha = 0,1$ durchgeführt.

$\overline{K} = [0,k]$

$P(X\leq k) \leq 0,1$

Dieses kannst du durch Systematisches Probieren mit Hilfe des BinomCdf-Befehl deines GTR bestimmen. Diesen findest du im Statistik-Menü unter

F5: DIST $\rightarrow$ F5: Binomial $\rightarrow$ F2: Bcd $\rightarrow$ F2: VAR

Du musst dann die entsprechenden Parameter eingeben.
Du erhältst beispielsweise folgende Ergebnisse:

$P(X \leq 400)\approx0,52$

$P(X \leq 350)\approx0,00000007$

$P(X \leq 380)\approx0,016$

$P(X \leq 385)\approx0,054$

$P(X \leq 390)\approx0,144$

$P(X \leq 388)\approx0,10044$

$P(X \leq 387)\approx0,083$

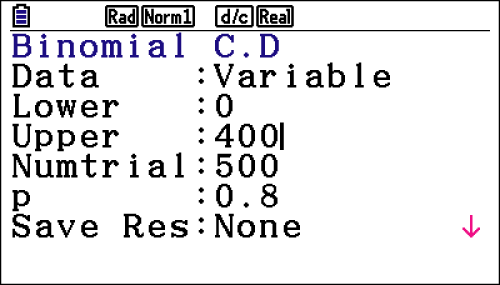
Bildschirmansicht einer statistischen Berechnung mit binomialen Daten und Parametern.

Damit ist das gesuchte $k = 387$ und die Entscheidungsregel lässt sich wie folgt formulieren:

$\blacktriangleright$ Wahrscheinlichkeit berechnen

$Y$ ist binomialverteilt mit den Parametern $n =500$ und $p =0 ,82$ . Berechne nun die gesuchte Wahrscheinlichkeit mit dem BinomCdf-Befehl deines GTR:

$P(Y \leq 387)\approx 0,005 = 0,5\,\%$

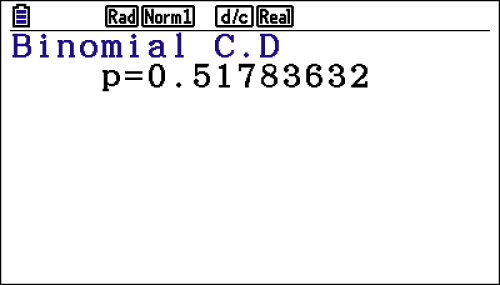
Die Wahrscheinlichkeit dafür, bei einer tatsächlichen Keimfähigkeit von $82\,\%$ die Nullhypothese zu verwerfen beträgt ca. $0,5\,\%$ .