Pflichtteil 1

Aufgabe 1

Gegeben ist die Funktion $f$ mit $f(x)= \mathrm e^{-2x+1}+1.$
Die Abbildung zeigt den Graphen $G_f$ sowie die Tangente an $G_f$ an der Stelle $x=\frac{1}{2}.$

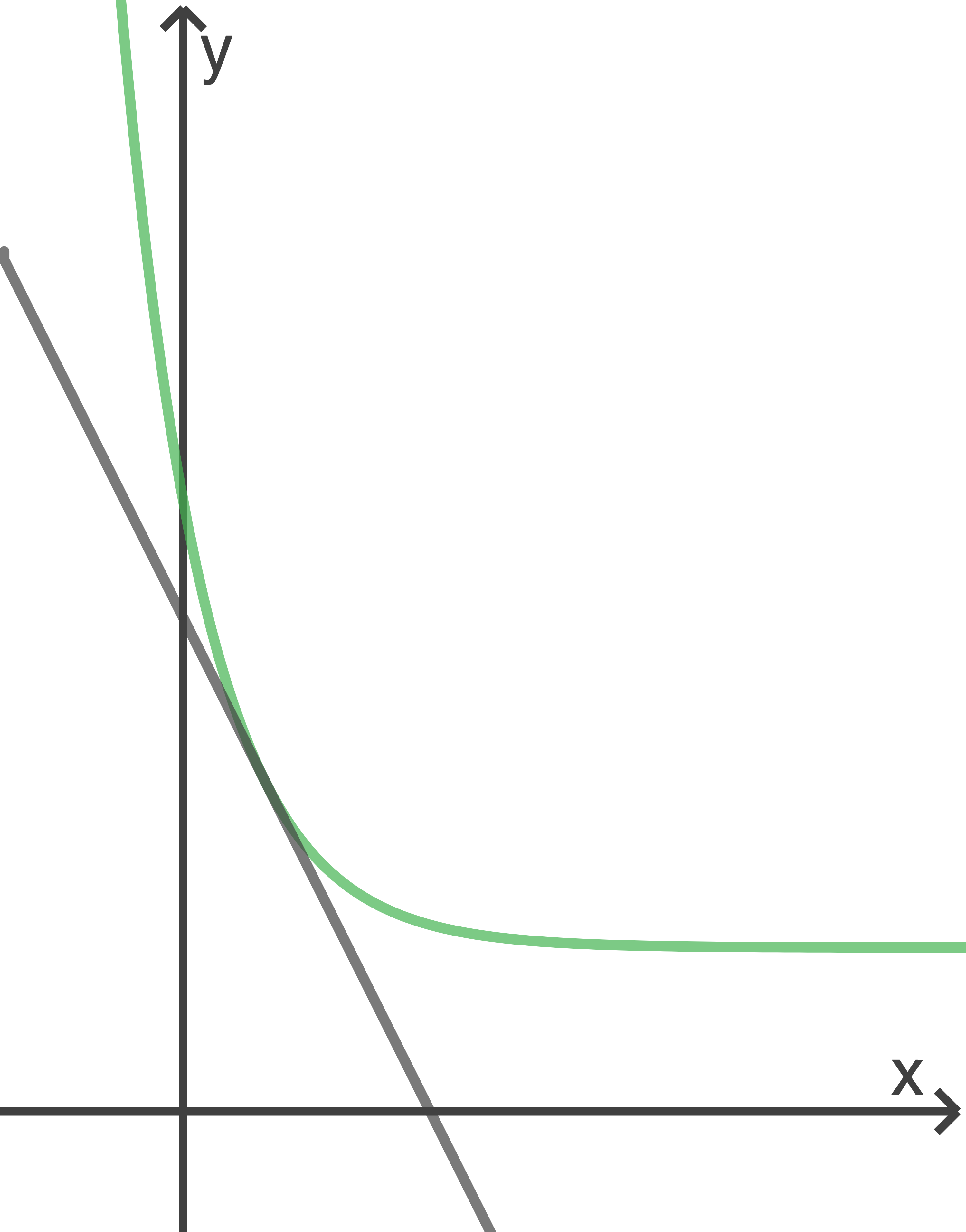
Grafik einer mathematischen Funktion mit Achsenbeschriftungen X und Y.

Weise nach, dass diese Tangente die Steigung $-2$ hat.

(1 VP)

Berechne den Flächeninhalt des Dreiecks, das diese Tangente mit den Koordinatenachsen einschließt.

(1,5 VP)

Aufgabe 2

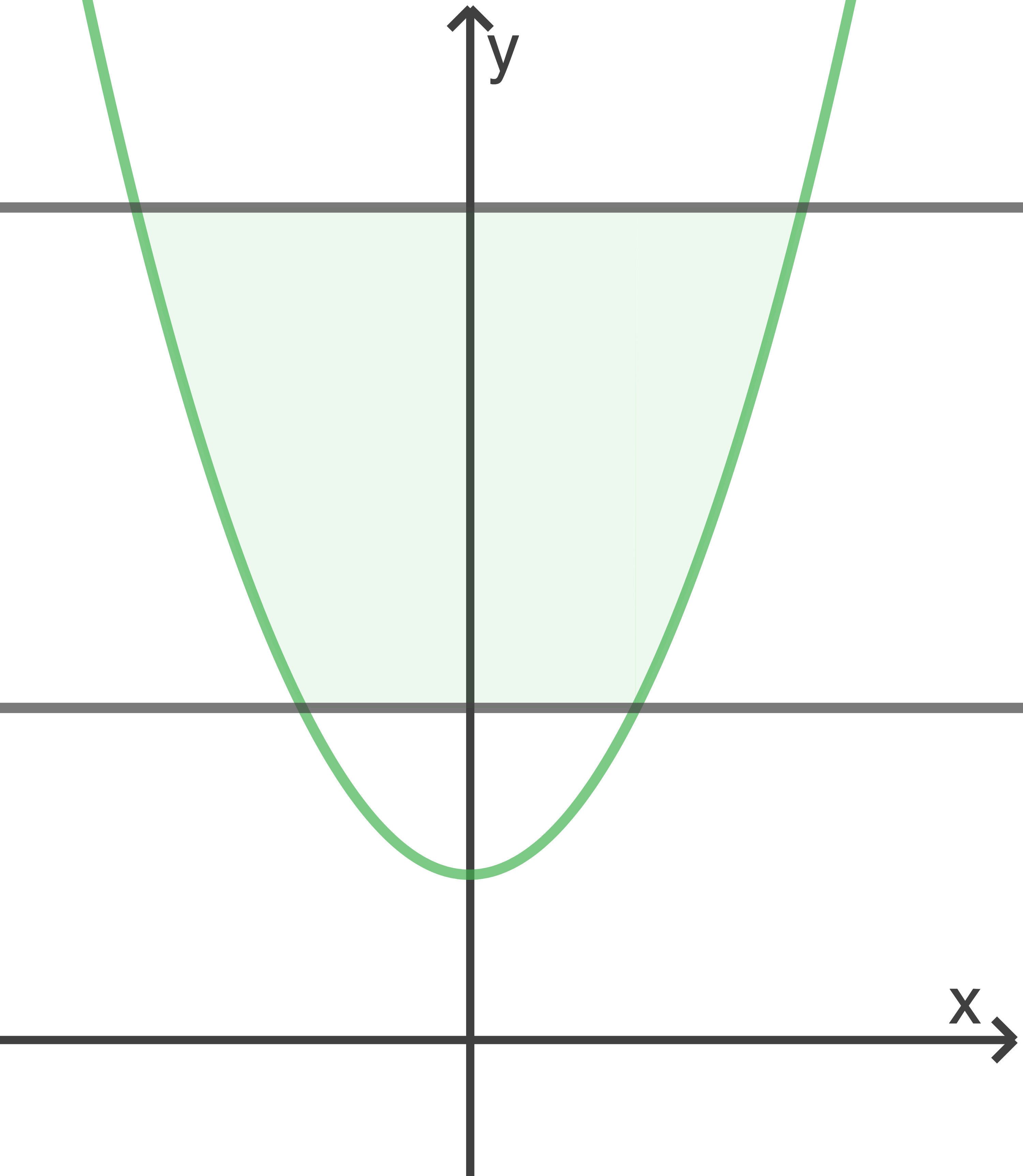
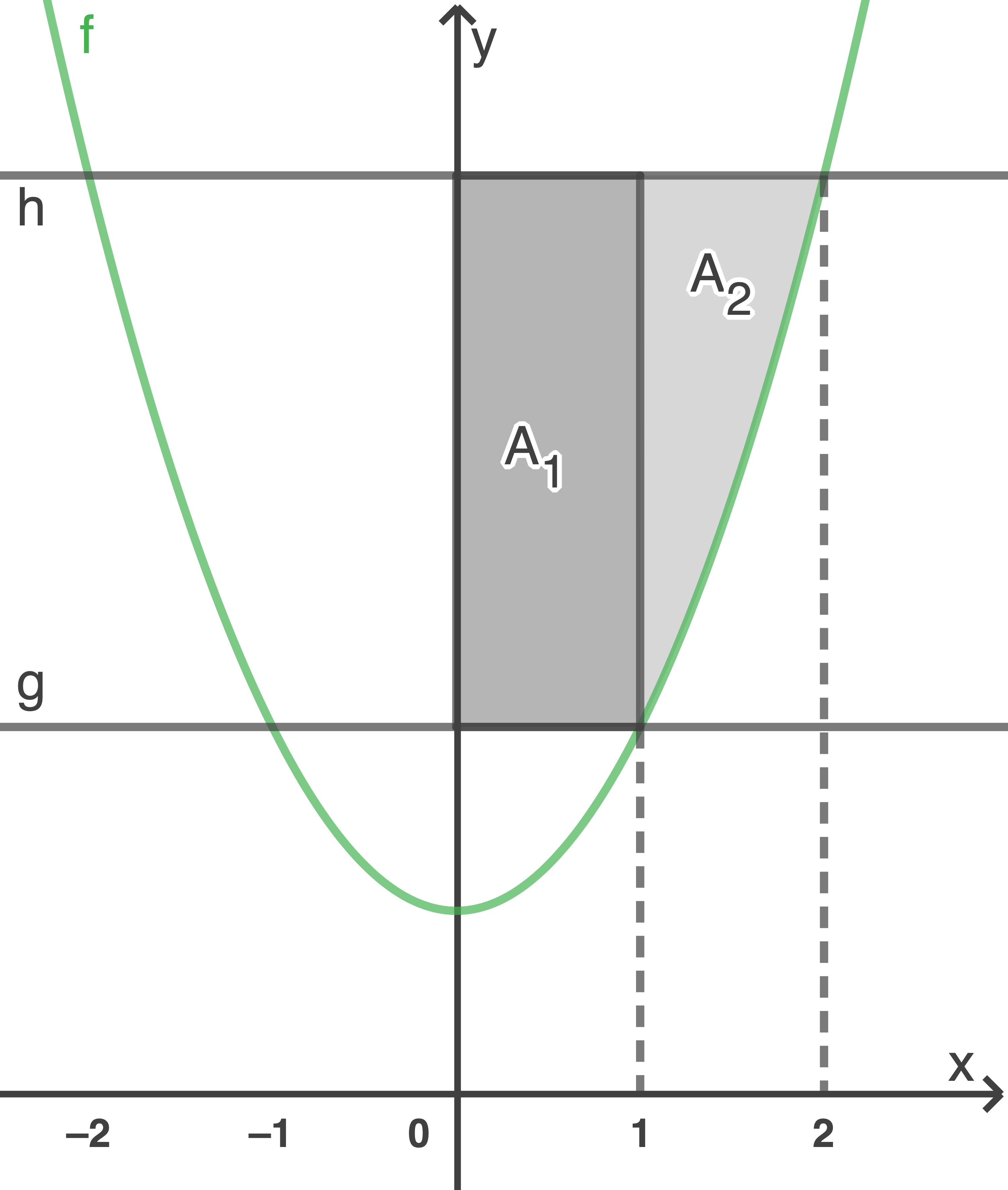
Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=1+x^2$ sowie die Geraden $g: y=2$ und $h: y=5.$
Bestimme den Inhalt der markierten Fläche.

Grafik einer Parabel mit Achsenbeschriftungen für x und y.

(2,5 VP)

Aufgabe 3

Gegeben sind die Funktionen $f$ und $g$ mit $f(x)=a+\dfrac{b}{x^2+c}$ und $g(x)=a+\dfrac{b}{(x+c)^2}.$
Die Abbildung zeigt den Graphen einer der beiden Funktionen sowie seine Asymptoten.

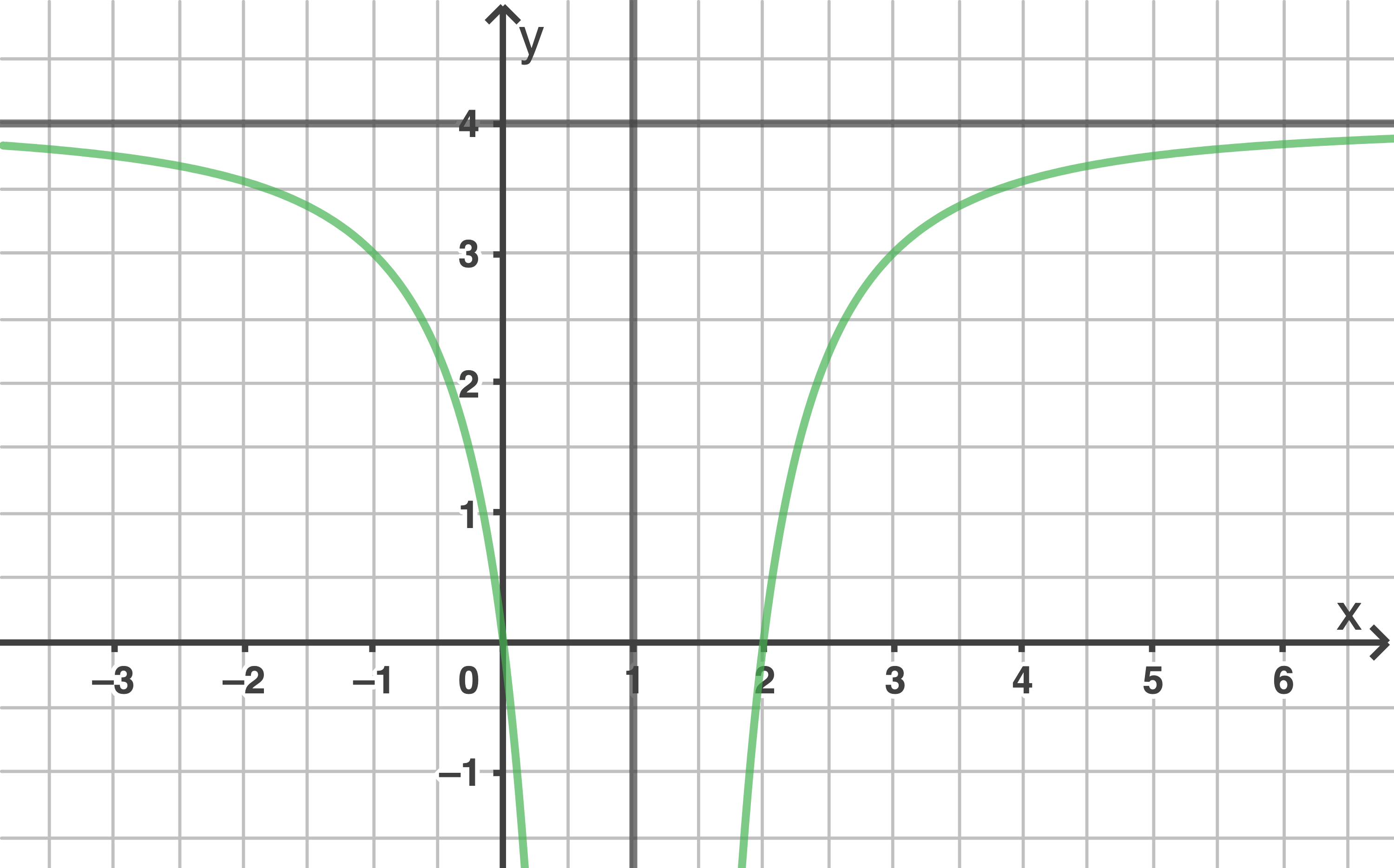
Graph einer mathematischen Funktion mit grüner Kurve im Koordinatensystem.

Begründe, dass es sich bei dem abgebildeten Graphen nicht um den Graphen von $f$ handeln kann.

(1 VP)

Bestimme für die Funktion $g$ die Werte von $a, b$ und $c.$

(1,5 VP)

Aufgabe 4

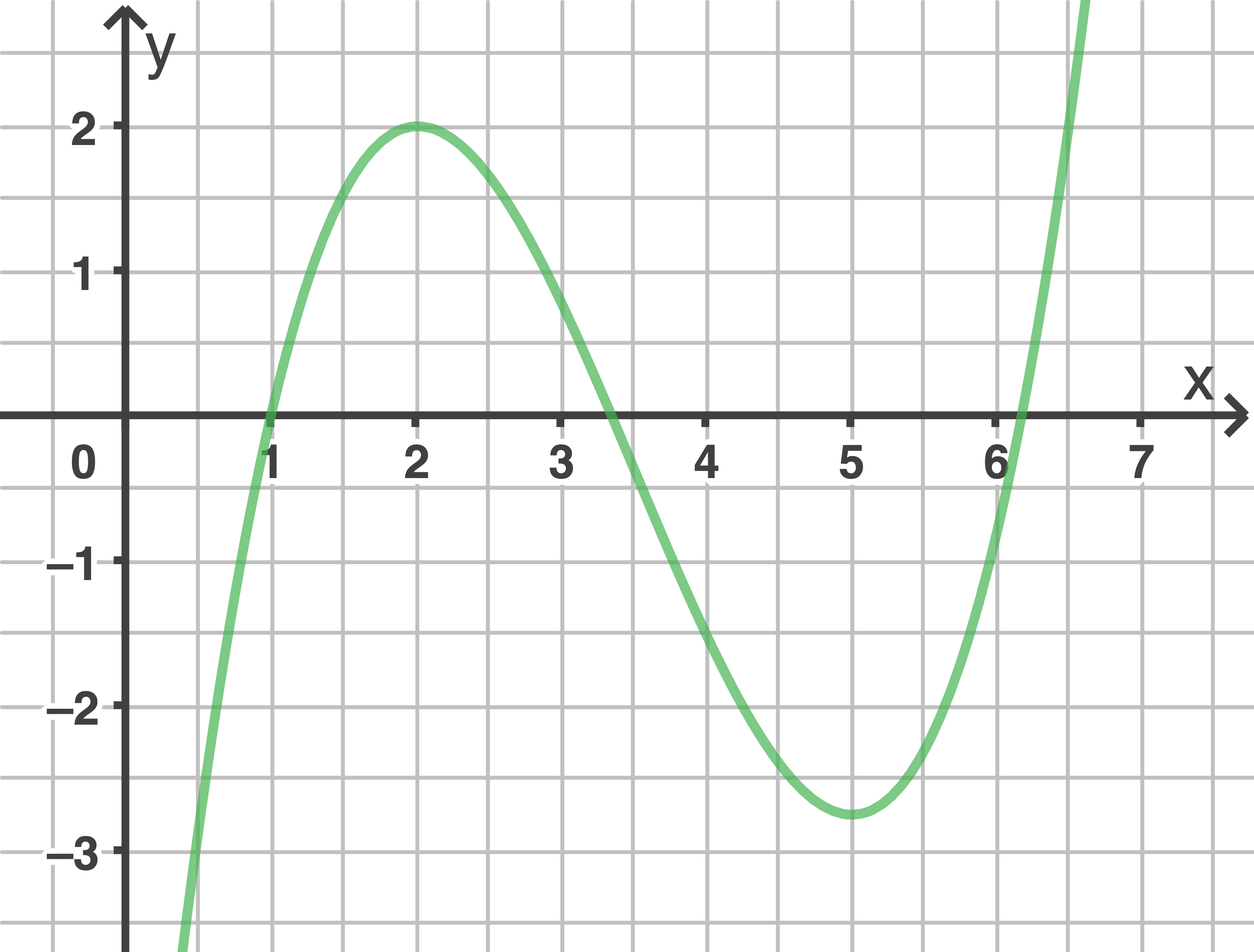
Die Abbildung zeigt den Graphen der Funktion $f$ . Die Funktion $g$ ist gegeben durch $g(x)=f(x)+5x.$
Entscheide jeweils, ob die folgenden Aussagen wahr oder falsch sind, und begründe deine Entscheidung.

Graf eines mathematischen Funktionsverlaufs mit Achsenbeschriftungen und einer grünen Kurve.

(1) Jede Stammfunktion von $f$ besitzt im Intervall $[0,5 ; 4]$ genau ein lokales Minimum.

(1 VP)

(2) Die Funktion $g$ ist im Intervall $[1; 6]$ streng monoton steigend.

(1,5 VP)

Aufgabe 5

Gegeben sind die Ebenen $E$ und $F$ sowie die Ebenenschar $G_r \; (r \in \mathbb{R}).$

$\begin{array}{llll} E:&x_1-5x_2-2x_3&=&6 &\quad \scriptsize \\ F:&2x_1-x_2-x_3&=& 3 &\quad \scriptsize \\ G_r: &9x_2+3x_3&=& r+11 &\quad \\ \end{array}$

Stelle die Ebene $G_7$ in einem Koordinatensystem dar.

(1 VP)

Für einen Wert von $r$ besitzen $E,$ $F$ und $G_r$ eine gemeinsame Schnittgerade. Bestimme diesen Wert von $r.$

(1,5 VP)

Aufgabe 6

Gegeben sind der Punkt $P(-1\mid 1\mid -1)$ und die Gerade $g:\overrightarrow{x}= \pmatrix{1\\-1\\7} +t \cdot \pmatrix{1\\2\\-2}$ , $t \in \mathbb{R}.$
Der Punkt $Q(3\mid 3\mid 3)$ liegt auf der Geraden $g.$

Zeige, dass $Q$ derjenige Punkt auf $g$ ist, der zu $P$ den kleinsten Abstand hat.

(1 VP)

Bestimme die Koordinaten eines Punktes $R$ auf der Geraden $g,$ für den das Dreieck $PQR$ den Flächeninhalt $27$ hat.

(1,5 VP)

Aufgabe 7

In einer Urne befinden sich vier schwarze und eine unbekannte Anzahl weißer Kugeln. Aus der Urne werden nacheinander zwei Kugeln mit Zurücklegen gezogen. Die Wahrscheinlichkeit, dabei zwei schwarze Kugeln zu ziehen, ist doppelt so groß wie die Wahrscheinlichkeit, zwei Kugeln unterschiedlicher Farbe zu ziehen.
Bestimme die Gesamtzahl der Kugeln in der Urne.

(2,5 VP)

Aufgabe 8

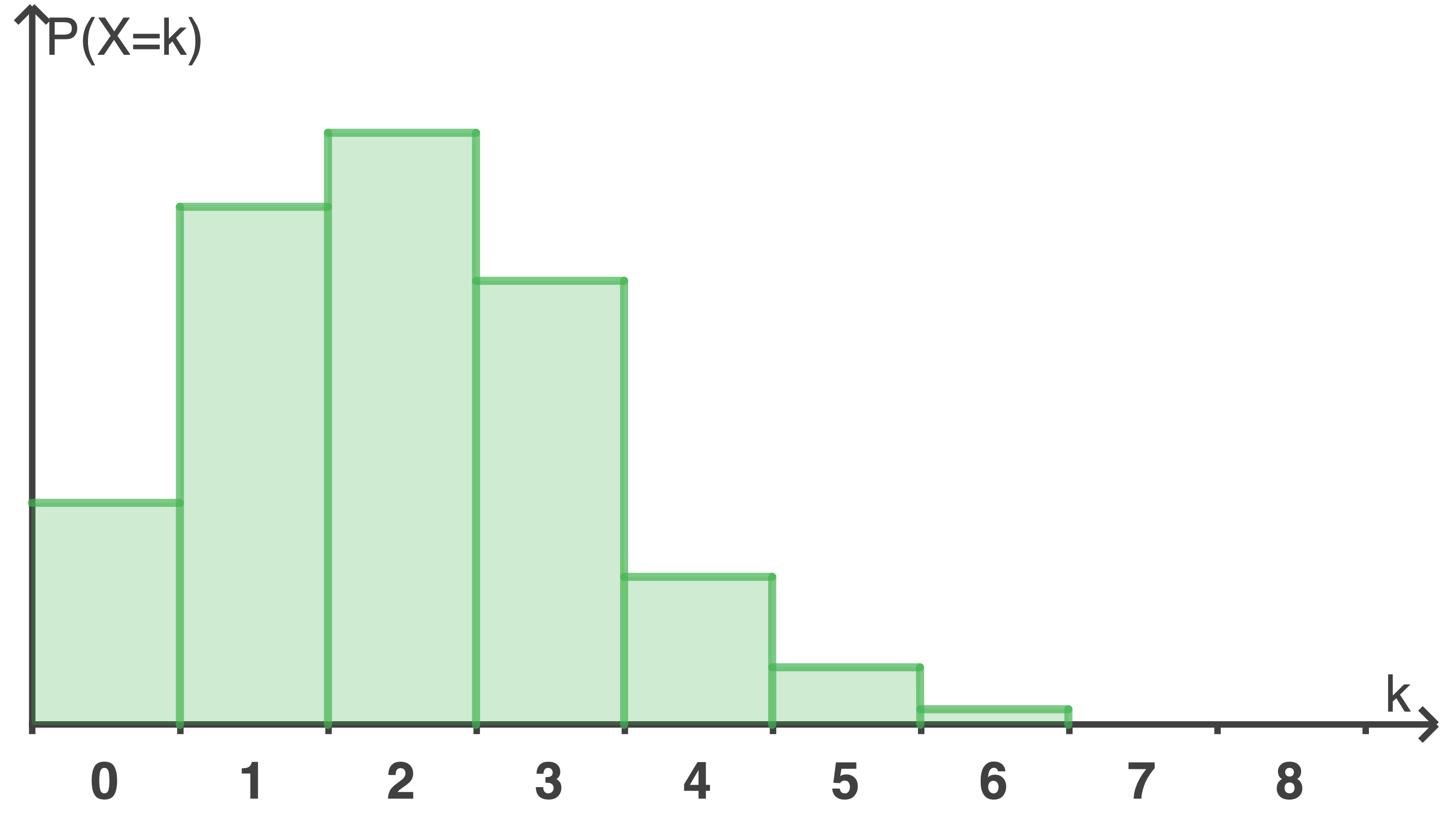
Die Abbildung stellt die Wahrscheinlichkeitsverteilung einer Zufallsgröße $X$ dar.

Histogramm zur Darstellung von Wahrscheinlichkeiten mit Achsen für P(X=k) und k.

Begründe, dass $P(X=2)\lt 0,5$ gilt.

(1 VP)

Für eine binomialverteilte Zufallsgröße $Y$ mit den Parametern $n=8$ und $0\lt p\lt 1$ gilt $P(Y=1)=2\cdot P(Y=0).$

Berechne den Wert von $p.$

(1,5 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\(\begin{array}[t]{rll} f$

1. Tangentengleichung aufstellen

Die Tangentengleichung lautet $t:y=-2x+c.$

$f \left(\frac{1}{2} \right) = \mathrm{e}^{-2\cdot \frac{1}{2}+1}+1 =2.$

Einsetzen von $\left(\frac{1}{2}\mid 2\right)$ in $t$ ergibt:

$\begin{array}[t]{rll} 2 &=& -2\cdot \dfrac{1}{2} +c \\[5pt] 2 &=& -1 +c &\quad \scriptsize \mid\; +1 \\[5pt] 3 &=&c \end{array}$

Die Tangentengleichung lautet demnach $t: y = -2x+3.$

2. Flächeninhalt berechnen

Die Tangente bildet mit den Koordinatenachsen ein rechtwinkliges Dreieck. Aus der Tangentengleichung kann der $y$ -Achsenabschnitt von $3$ abgelesen werden.
Für die Schnittstelle mit der $x$ -Achse folgt:

$\begin{array}[t]{rll} 0 &=& -2x +3 &\quad \scriptsize \mid\; +2x \\[5pt] 2x &=& 3 &\quad \scriptsize \mid\; :2 \\[5pt] x &=& \frac{3}{2} \end{array}$

Für den Flächeninhalt folgt:

$A= \frac{1}{2} \cdot 3 \cdot \frac{3}{2}=\frac{9}{4}$

Der Flächeninhalt beträgt $\frac{9}{4} \,\text{FE}.$

Lösung 2

Diagramm einer Parabel mit beschatteten Flächen A1 und A2, Achsen x und y beschriftet.

Es genügt die rechte Hälfte der Fläche zu betrachten. Diese lässt sich in zwei Teilflächen aufteilen. Die Begrenzungen werden durch die Schnittstellen von $f$ mit $g$ und $h$ festgelegt.

$\begin{array}[t]{rll} f(x) &=& g(x) \\[5pt] 1+x^2 &=& 2 &\quad \scriptsize \mid\;-1 \\[5pt] x^2 &=& 1 \\[5pt] x &=& \pm 1 \\[10pt] f(x) &=& h(x) \\[5pt] 1+x^2 &=& 5 &\quad \scriptsize \mid\;-1 \\[5pt] x^2 &=& 4 \\[5pt] x &=& \pm 2 \\[5pt] \end{array}$

Bei einer der beiden Teilflächen handelt es sich um ein Rechteck, bei der anderen um die Fläche, die der Graph von $f$ mit der Geraden zu $h$ begrenzt.

Rechenweg anzeigen

$A=\frac{28}{3}\,\text{[FE]}$

Lösung 3

Die Abbildung zeigt nicht den Graphen von $f$ , da der Graph von $f$ symmetrisch zur $y$ -Achse ist mit $f(-x)=f(x).$

Aus der Abbildung geht hervor, dass der Graph von $g$ die Asymptoten $y=4$ und $x=1$ hat. Daraus ergeben sich $a=4$ und $c=-1.$ Durch Einsetzen von $(0\mid 0),$ ergibt sich $b=-4.$

Lösung 4

(1)

Es handelt sich um eine wahre Aussage, denn im angegebenen Intervall wechselt $f$ nur an der Stelle $x=1$ das Vorzeichen von negativ zu positiv.

(2)

Es gilt $\(g$ und aus der Abbildung kann entnommen werden, dass $\(f$ in $[1;6]$ nur größere Werte als $-5$ annimmt. Es gilt somit $\(g$ in $[1;6]$ , weshalb $g$ streng monoton steigend ist und die Aussage wahr.

Lösung 5

Die Schnittstellen mit den Koordinatenachsen liegen bei $x_2=2$ und $x_3=6.$

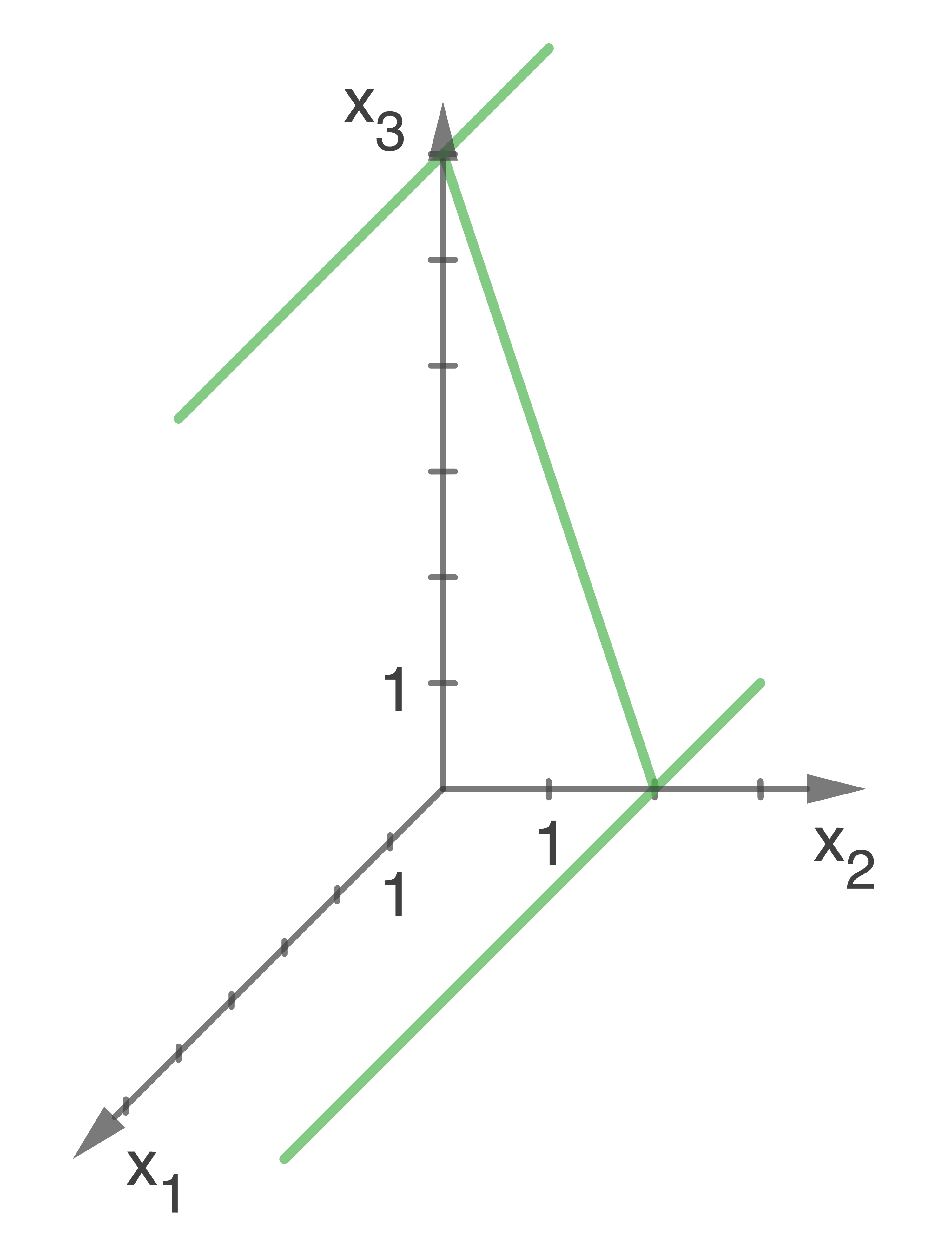
Grafische Darstellung eines dreidimensionalen Koordinatensystems mit Achsen x1, x2 und x3.

Gleichungssystem anzeigen

$E,F$ und $G_r$ haben eine gemeinsame Schnittgerade für $r=-20.$

Lösung 6

$\overrightarrow{PQ}=\pmatrix{4\\2\\4}$

$P$ hat den kleinsten Abstand zu $Q,$ wenn $\overrightarrow{PQ}$ senkrecht zur Geraden $g$ verläuft, wenn also das Skalarprodukt von $\overrightarrow{PQ}$ mit dem Richtungsvektor der Geraden gleich Null ist.

$\pmatrix{4\\2\\4} \circ \pmatrix{1\\2\\-2} = 4+4-8=0$

$Q$ ist also der Punkt auf $g$ mit dem kürzesten Abstand zu $P.$

Für den Flächeninhalt gilt:

$A = \dfrac{1}{2}\cdot \left| \overrightarrow{PQ} \right| \cdot \left| \overrightarrow{QR} \right| = 27\,\text{[FE]}$

$\left| \overrightarrow{PQ} \right| = \left| \pmatrix{4\\2\\4} \right| =6\,\text{[LE]}$

Daraus folgt also:

$\left| \overrightarrow{QR} \right| = \dfrac{27\cdot 2}{6} = 9\,\text{[LE]}$

Rechenweg anzeigen

Somit ist $R(6 \mid 9 \mid -3).$

Lösung 7

Es gilt: $P(ss) = 2 \cdot (P(ws) +P(sw))$

$a$ stellt die Gesamtzahl der Kugeln in der Urne dar.

Mit den Pfadregeln gilt:

$P(ss)= \left( \dfrac{4}{a}\right)^2 = \frac{16}{a^2}$

$P(ws) = \frac{a-4}{a}\cdot \frac{4}{a} = \frac{4\cdot (a-4)}{a^2}$ bzw. $P(sw) = \frac{4}{a}\cdot \frac{a-4}{a} = \frac{4\cdot (a-4)}{a^2}$

Einsetzen in die oben angegebene Gleichung liefert:

Vollständigen Rechenweg anzeigen

$a=5$

Es sind insgesamt 5 Kugeln in der Urne.

Lösung 8

Die Balken in der Abbildung stellen die Wahrscheinlichkeiten der binomialverteilten Zufallsgröße $X$ dar. Die Summe dieser Wahrscheinlichkeiten muss exakt $1$ ergeben.

Aus der Abbildung lässt sich entnehmen, dass $P(X= 0) +P(X= 1)\gt P(X=2)$ gilt.

Wäre $P(X=2)$ größer oder gleich $0,5$ wäre $P(X= 0) +P(X= 1)$ erstrecht größer als $0,5$ und somit die Summe aller Wahrscheinlichkeiten größer als $1.$
Da dies bei einer Wahrscheinlichkeitsverteilung nicht möglich ist, muss also $P(X=2) \lt 0,5$ sein.

Rechenweg anzeigen

Es folgt $p=\dfrac{1}{5}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?