Wahlteil A1
Aufgabe A1.1
Gegeben ist die Funktion  mit
mit  .
.
Ihr Graph ist .
.
Ihr Graph ist
a)
(4 VP)
b)
Für jedes  sind
sind  ,
,  und
und  die Eckpunkte eines Dreiecks.
Bestimme einen Wert für
die Eckpunkte eines Dreiecks.
Bestimme einen Wert für  so, dass dieses Dreieck den Flächeninhalt
so, dass dieses Dreieck den Flächeninhalt  hat.
Für welchen Wert von
hat.
Für welchen Wert von  ist das Dreieck gleichschenklig?
ist das Dreieck gleichschenklig?
(4 VP)
c)
Auf der  -Achse gibt es Intervalle der Länge
-Achse gibt es Intervalle der Länge  auf denen die Funktion
auf denen die Funktion  den Mittelwert
den Mittelwert  besitzt.
Bestimme die Grenzen eines solchen Intervalls.
besitzt.
Bestimme die Grenzen eines solchen Intervalls.
(3 VP)
Aufgabe A1.2
Gegeben ist für jedes  eine Funktion
eine Funktion  durch
durch  .
Bestimme
.
Bestimme  so, dass die beiden Extrempunkte des Graphen von
so, dass die beiden Extrempunkte des Graphen von  den Abstand
den Abstand  voneinander haben.
voneinander haben.
(4 VP)
Lösung A1.1
a)  Koordinate des Extrempunktes
Koordinate des Extrempunktes  angeben
angeben

 ist ihr Schaubild. Deine Aufgabe ist es, die Koordinaten des Extrempunktes
ist ihr Schaubild. Deine Aufgabe ist es, die Koordinaten des Extrempunktes  zu bestimmen.
zu bestimmen.
![\(\begin{array}[t]{rll}
f(x)&=& 10 \cdot x \cdot \mathrm{e}^{-0,5 \cdot x}&
\end{array}\)](https://mathjax.schullv.de/e2508b4a9218ba400116327e53e885082fa6c3aac2087f029f4af575ffd6cad2?color=5a5a5a)


![\(\begin{array}[t]{rll}
f‘(x)&=& \mathrm{e}^{-0,5 \cdot x}\cdot (10 - 5 \cdot x) & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c7f39dca8a8d2aa9e05195b53ba3ecdbb9acaa1db9c9675ebb86238f5c788e47?color=5a5a5a)


 Koordinate des Wendepunktes
Koordinate des Wendepunktes  angeben
angeben



![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/b18b561c333e23efcb3aadf478c9bb9ce41b4f9caa6d6b24194867625a8a51b2?color=5a5a5a)

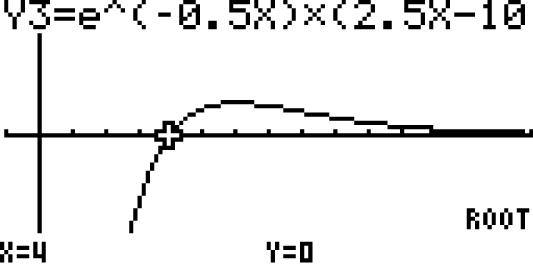
 Gleichung der Asymptote von
Gleichung der Asymptote von  angeben
angeben
 und
und 
 und
und 
 Skizzieren des Schaubildes
Skizzieren des Schaubildes 
Gegeben ist der Funktionsterm einer Funktion  mit:
mit:
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  .
.
Diese erhältst du, indem du die Produktregel anwendest:
Diese erhältst du, indem du die Produktregel anwendest:
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
Damit hast du eine potentielle Extremstelle an  ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.

Alternativ bietet es sich auch an, die potentielle Extremstelle mit dem GTR zu bestimmen:
Gib dazu den Term der ersten Ableitungsfunktion ƒ‘ an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
Gib dazu den Term der ersten Ableitungsfunktion ƒ‘ an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
|
menu |
den Befehl zum Bestimmen der Nullstelle aus und bestätige mit Enter.
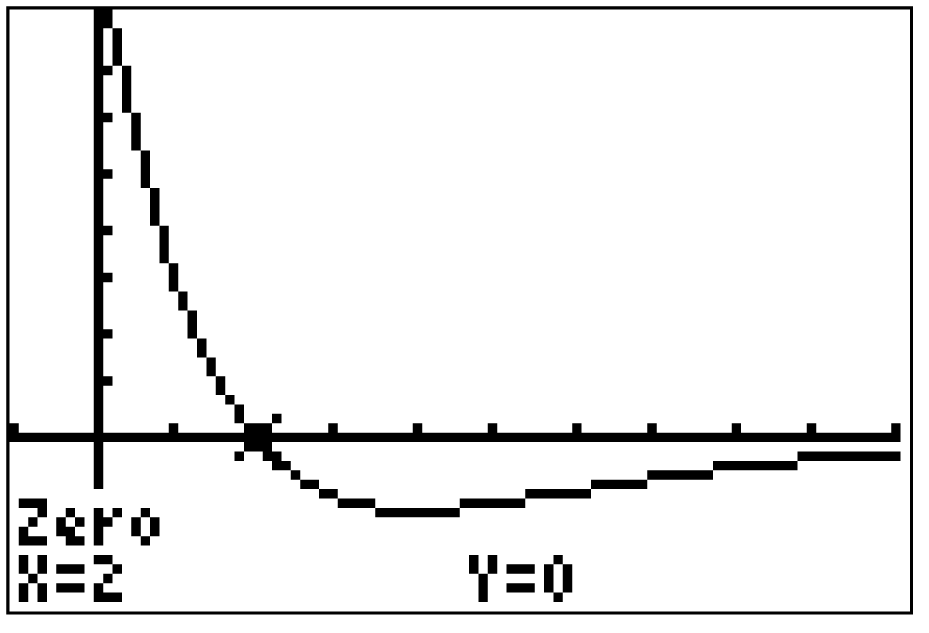
Der GTR liefert dir eine potentielle Extremstelle an  .
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Extremstelle vorliegt. Wegen
eine Extremstelle vorliegt. Wegen  kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes ermittelt. Die
-Koordinate des Hochpunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:

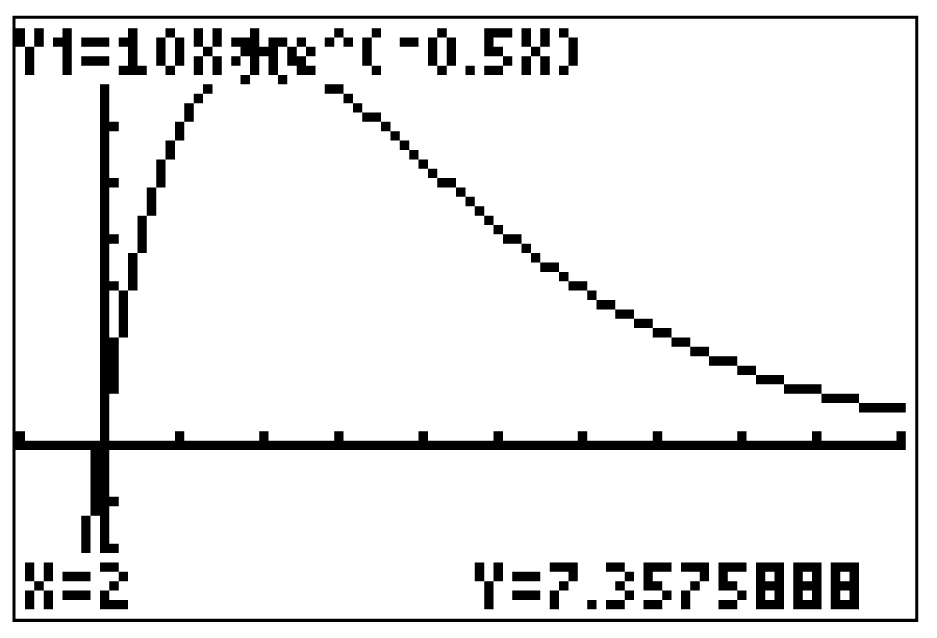
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen.
auch mit Hilfe des GTR bestimmen.
Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle
im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
|
menu |
Die Koordinaten des Extrempunktes  lauten
lauten  .
.
Laut Aufgabenstellung besitzt das Schaubild  einen Wendepunkt. Um dessen Koordinaten angeben zu können, musst du zunächst die Wendestelle
einen Wendepunkt. Um dessen Koordinaten angeben zu können, musst du zunächst die Wendestelle  der Funktion
der Funktion  bestimmen. Für diese Wendestelle müssen folgende Bedingungen erfüllt sein:
bestimmen. Für diese Wendestelle müssen folgende Bedingungen erfüllt sein:
- Notwendige Bedingung:
- Hinreichende Bedingung:
Hast du anschließend  bestimmt, so kannst du die Wendestelle in den Term der Funktion
bestimmt, so kannst du die Wendestelle in den Term der Funktion  einsetzen und so die
einsetzen und so die  -Koordinate des Wendepunktes bestimmen.
-Koordinate des Wendepunktes bestimmen.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Wendestelle der Funktion  zu überprüfen, benötigst du die zweite Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die zweite Ableitungsfunktion der Funktion  . Diese hast du zuvor mit Hilfe der Produktregel bestimmt:
. Diese hast du zuvor mit Hilfe der Produktregel bestimmt:
Für die hinreichende Bedingung muss  gelten:
gelten:
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
Damit hast du eine potentielle Wendestelle an  ermittelt.
ermittelt.

Alternativ bietet es sich auch an, die potentielle Wendestelle mit dem GTR zu bestimmen:
Gib dazu den Term der zweiten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
Gib dazu den Term der zweiten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
|
menu |
den Befehl zum Bestimmen der Nullstelle aus und bestätige mit Enter.
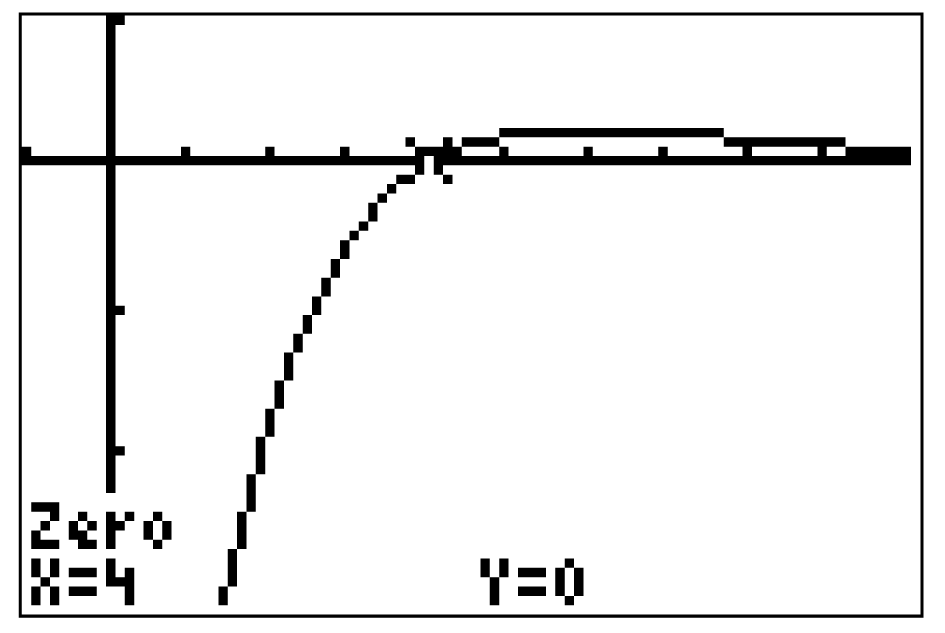
Der GTR liefert dir eine potentielle Wendestelle an  .
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Wendestelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die dritte Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die dritte Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Wendestelle liegt.
eine Wendestelle liegt.
3. Schritt: Koordinaten des Wendepunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Wendepunkt befindet. Damit hast du die
ein Wendepunkt befindet. Damit hast du die  -Koordinate des Wendepunktes ermittelt. Die
-Koordinate des Wendepunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:

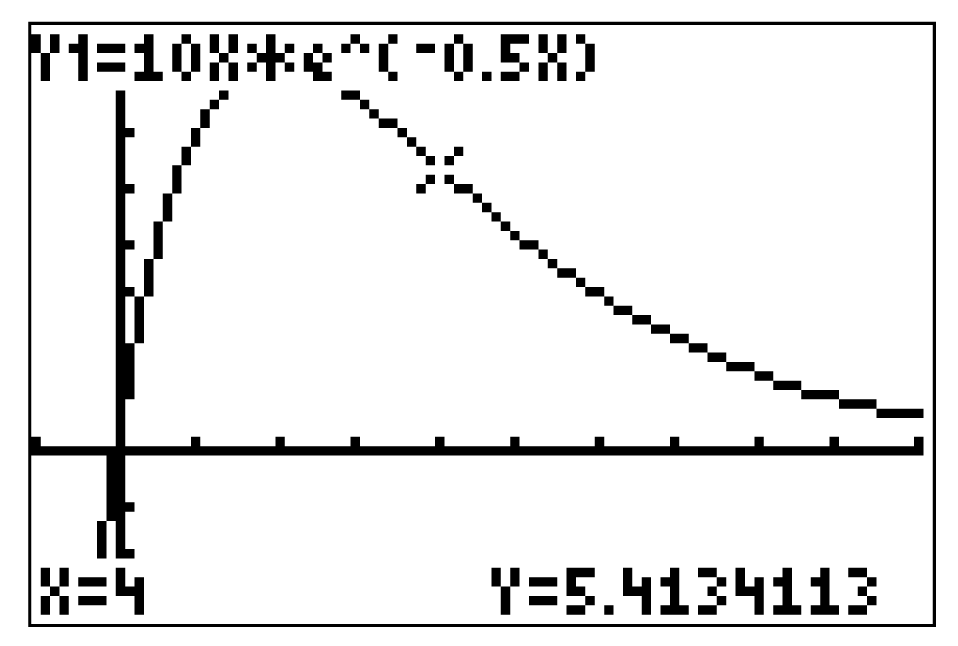
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion
auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle
im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
|
menu |
Die Koordinaten des des Wendepunktes  lauten
lauten  .
.

Betrachte das Schaubild der Funktion  in deinem GTR.
in deinem GTR.
Deine Aufgabe ist es, die Gleichung der Asymptote von anzugeben.
anzugeben.
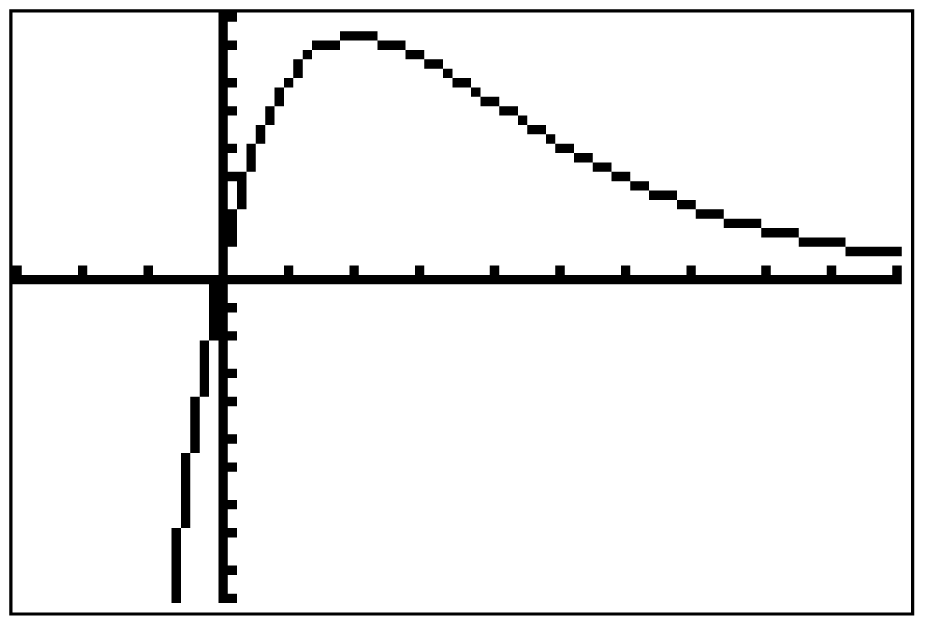
Anhand des Schaubildes (Abbildung links) kannst du bereits vermuten, dass es sich um eine waagrechte Asymptote handelt.
Um die Gleichung der Asymptote zu bestimmen, kannst du die Funktion für
für  und für
und für  untersuchen.
untersuchen.
Deine Aufgabe ist es, die Gleichung der Asymptote von
Anhand des Schaubildes (Abbildung links) kannst du bereits vermuten, dass es sich um eine waagrechte Asymptote handelt.
Um die Gleichung der Asymptote zu bestimmen, kannst du die Funktion
Untersuchen für  :
:
Der Funktionsterm von  ist gegeben durch
ist gegeben durch  .
.
Betrachtest du , so kannst du festhalten, dass gilt:
, so kannst du festhalten, dass gilt:
Betrachtest du
Da der  -Term den dominanten Term darstellt, konvergiert die Funktion
-Term den dominanten Term darstellt, konvergiert die Funktion  für
für  gegen 0.
gegen 0.
Die Gleichung der Asymptote lautet also .
.
Die Gleichung der Asymptote lautet also
Untersuchen für  :
:
Betrachtest du noch  , so kannst du festhalten, dass gilt:
, so kannst du festhalten, dass gilt:
Da auch hier der  -Term den dominanten Term darstellt, strebt die Funktion
-Term den dominanten Term darstellt, strebt die Funktion  für
für  gegen
gegen  . Damit liegt keine weitere Asymptote vor.
. Damit liegt keine weitere Asymptote vor.
Weiterhin verlangt die Aufgabenstellung, das Schaubild  zu skizzieren. Dabei kannst du folgende Angaben verwenden:
zu skizzieren. Dabei kannst du folgende Angaben verwenden:
- Betrachte das Schaubild in deinem GTR, indem du den Graph-Modus auswählst.
- Verwende, dass sich der Hochpunkt an
und der Wendepunkt an
befindet.
- Für
konvergiert die Funktion gegen 0, für
strebt sie gegen
.
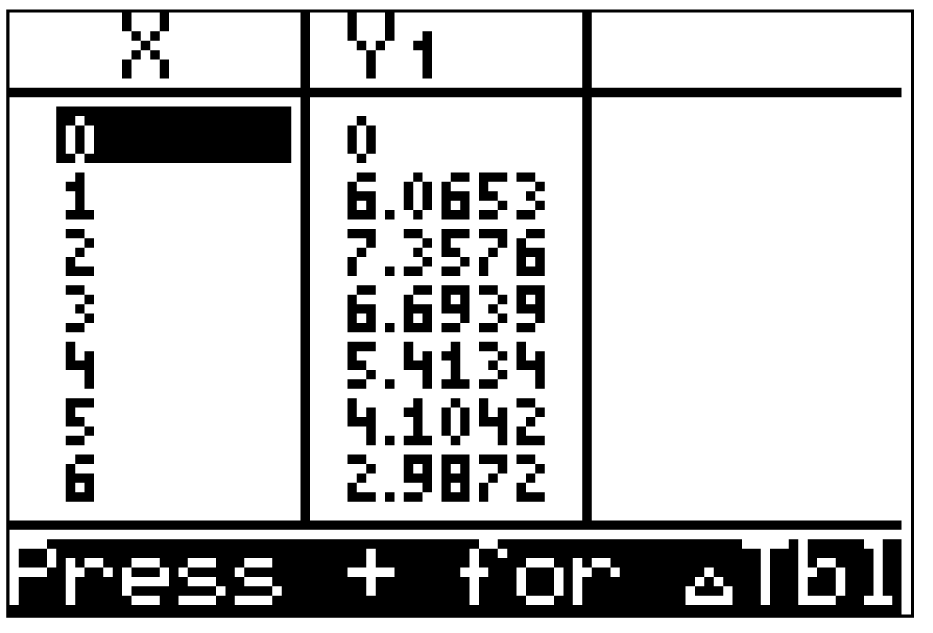
Zusätzlich kannst du dir noch die zugehörige Wertetabelle der Funktion einblenden lassen. Diese findest du im Graph-Modus unter TABLE:

Das Schaubild  sollte dann folgendermaßen aussehen:
sollte dann folgendermaßen aussehen:

b)  Wert für
Wert für  bestimmen, sodass der Flächeninhalt 8 FE beträgt
bestimmen, sodass der Flächeninhalt 8 FE beträgt


![\(\begin{array}[t]{rll}
A(u)&=& \frac{1}{2} \cdot u \cdot 10 \cdot u \cdot \mathrm{e}^{-0,5 \cdot u}&\\[5pt]
&=& 5 \cdot u^2 \cdot \mathrm{e}^{-0,5 \cdot u}
\end{array}\)](https://mathjax.schullv.de/e7cf31b98e460bf7929e1157ae8a30e0fc6ee8bc7a3ad3539b2760a5d08d498f?color=5a5a5a)
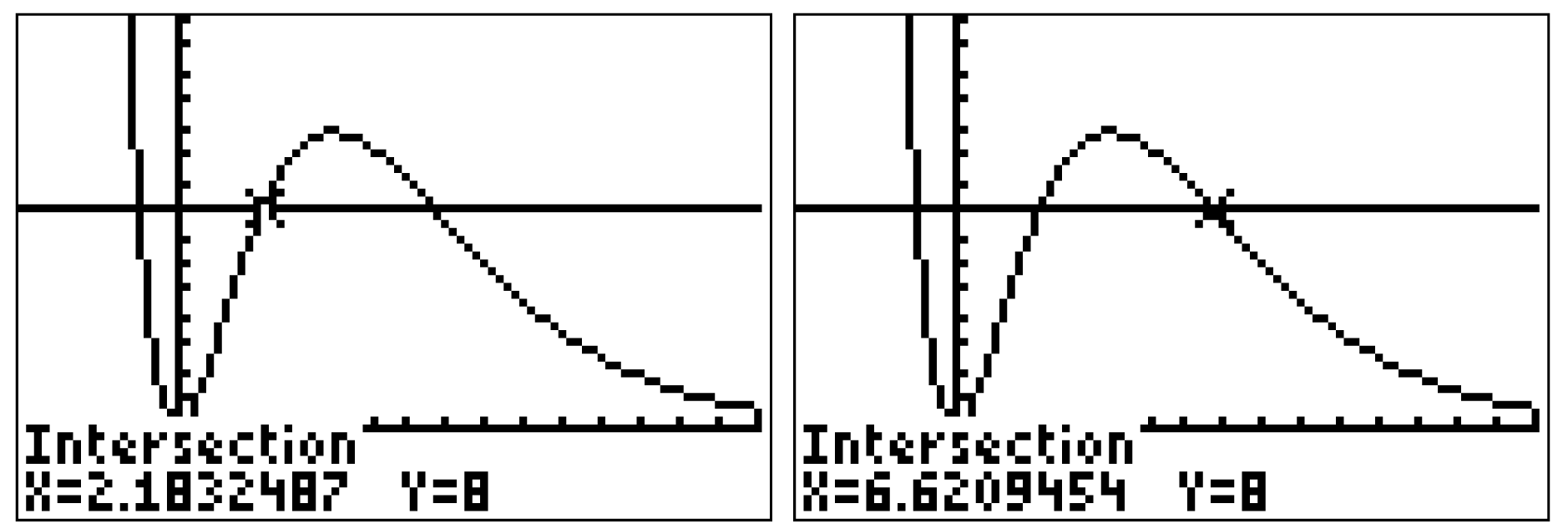
 Wert für
Wert für  bestimmen, sodass das Dreieck gleichschenklig ist
bestimmen, sodass das Dreieck gleichschenklig ist
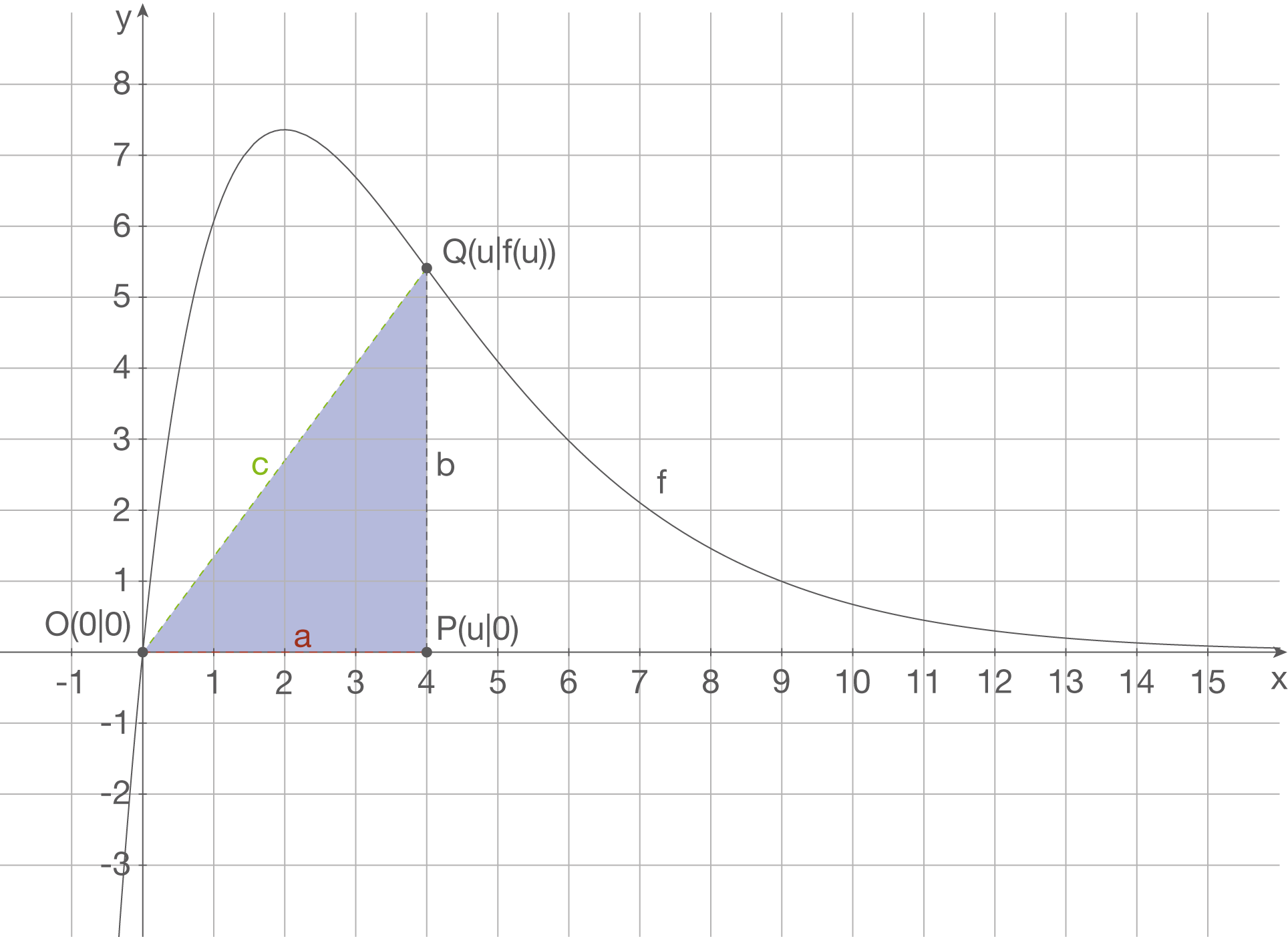


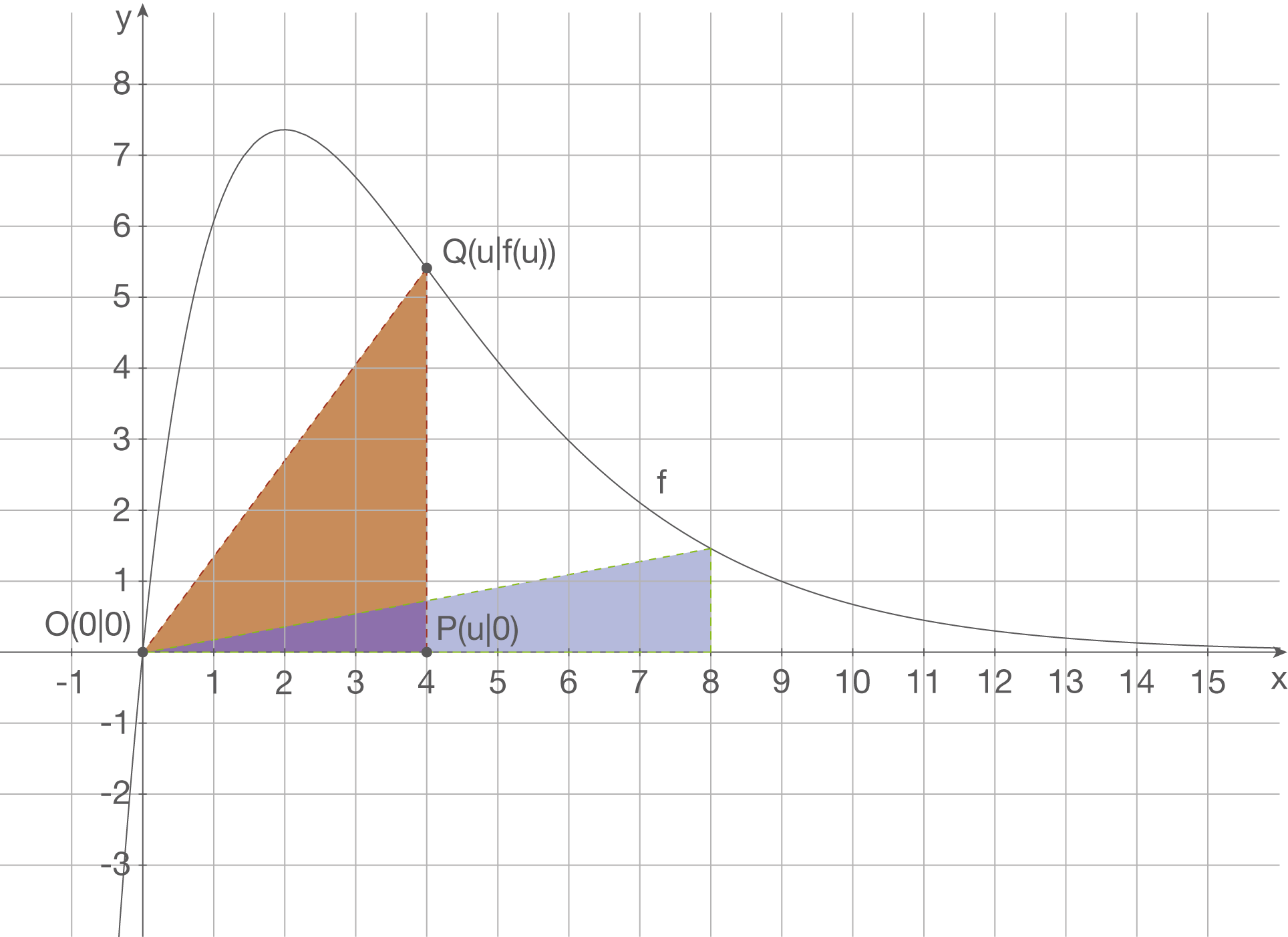
Gegeben sind die Punkte  ,
,  und
und  . Sie stellen die Eckpunkte eines Dreiecks dar.
. Sie stellen die Eckpunkte eines Dreiecks dar.
Deine Aufgabe ist es, einen Wert für so zu bestimmen, dass der Flächeninhalt des Dreieck 8 FE beträgt.
so zu bestimmen, dass der Flächeninhalt des Dreieck 8 FE beträgt.
Deine Aufgabe ist es, einen Wert für

Der Flächeninhalt  eines Dreiecks berechnet sich allgemein über folgenden Zusammenhang:
eines Dreiecks berechnet sich allgemein über folgenden Zusammenhang:
Dabei stellt  die Länge der Grundseite und
die Länge der Grundseite und  die Länge der Höhe dar.
die Länge der Höhe dar.
Um einen passenden Wert für zu ermitteln, kannst du wie folgt vorgehen:
zu ermitteln, kannst du wie folgt vorgehen:
Um einen passenden Wert für
- Stelle die Flächenfunktion in Abhängigkeit vom Parameter
auf.
- Setze den resultierenden Term mit 8 gleich und löse nach
auf, um den gesuchten Wert zu erhalten.
Den zweiten Schritt kannst du mit Hilfe deines GTR durchführen.
1. Schritt: Flächenfunktion aufstellen
Anhand der Abbildung kannst du erkennen, dass die Grundseite dem Wert  und die Höhe dem Funktionswert
und die Höhe dem Funktionswert  entspricht. Dadurch erhältst du folgende von
entspricht. Dadurch erhältst du folgende von  abhängige Flächenfunktion
abhängige Flächenfunktion  :
:
Setze den Funktionsterm von  ein, um den vollständigen Term er Flächenfunktion
ein, um den vollständigen Term er Flächenfunktion  zu erhalten:
zu erhalten:
2. Schritt: Wert für Parameter  ermitteln
ermitteln
Um einen passenden Wert für  zu erhalten, sodass der Flächeninhalt 8 FE beträgt, kannst du den aufgestellten Term der Flächenfunktion mit 8 gleichsetzen und nach
zu erhalten, sodass der Flächeninhalt 8 FE beträgt, kannst du den aufgestellten Term der Flächenfunktion mit 8 gleichsetzen und nach  auflösen. Da dieser Weg rechnerisch sehr aufwendig ist, wählen wir die graphische Lösung des Problems mit Hilfe des GTR:
auflösen. Da dieser Weg rechnerisch sehr aufwendig ist, wählen wir die graphische Lösung des Problems mit Hilfe des GTR:
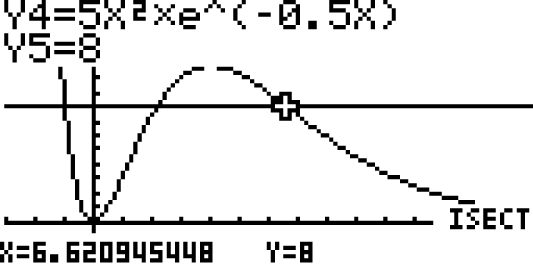
- Gib den Funktionsterm
im GTR ein.
- Gib weiterhin eine Gerade mit der Gleichung y = 8 an und lass beide im Graph-Modus anzeigen.
- Bestimme die Schnittstelle der beiden Schaubilder. Diese entspricht gerade dem gesuchten Wert für
.


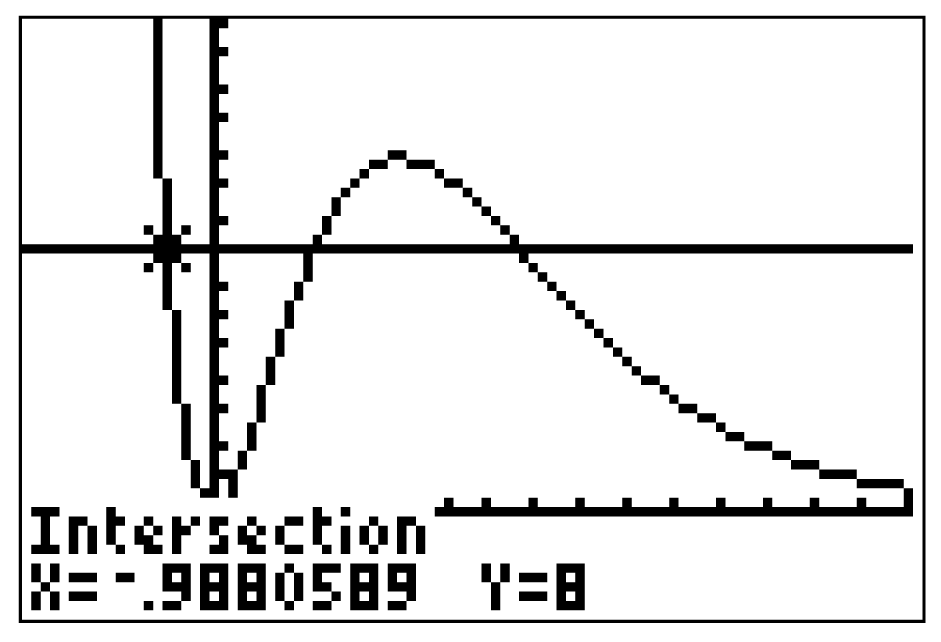
Der GTR liefert dir drei verschiedene Werte für  , sodass der Flächeninhalt 8 FE beträgt.
, sodass der Flächeninhalt 8 FE beträgt.
Da aber laut Aufgabenstellung gelten soll, kannst du das Resultat
gelten soll, kannst du das Resultat  vernachlässigen.
vernachlässigen.
Da aber laut Aufgabenstellung
Damit hast du zwei passende Werte für  ermittelt mit
ermittelt mit
,
.

Damit das Dreieck gleichschenklig ist, muss einer der folgenden Fälle eintreten:
oder
oder
.
Gib dazu zunächst die Länge der Seiten  ,
,  und
und  in Abhängigkeit von
in Abhängigkeit von  an und setze diese gleich, um so einen passenden Parameterwert für
an und setze diese gleich, um so einen passenden Parameterwert für  zu ermitteln.
zu ermitteln.
1. Schritt: Länge der Seiten in Abhängigkeit von  angeben
angeben
- Die Seitenlänge
entspricht dem Abstand vom Ursprung
zum Punkt
. Dieser Abstand ist gerade gleich
.
- Die Seitenlänge
stellt den Abstand zwischen den Punkten
und
dar. Da diese die gleiche
-Koordinate haben, besitzen sie einen Abstand von
.
berechnet sich mit Hilfe des Satzes von Pythagoras:
2. Schritt: Seitenlängen gleichsetzen, um  zu bestimmen
zu bestimmen
Damit das Dreieck gleichschenklig ist, können die oben genannten drei Fälle  ,
,  oder
oder  eintreten. Wir überprüfen zunächst, ob für den Fall
eintreten. Wir überprüfen zunächst, ob für den Fall  ein
ein  existiert:
existiert:
1. Fall: 
Mit dem Satz vom Nullprodukt folgt, dass die Gleichung nur für  gelöst werden kann. Da aber für
gelöst werden kann. Da aber für  kein Dreieck zustande kommt, kannst du diesen Wert vernachlässigen. Geometrisch interpretiert heißt das, dass die Seiten
kein Dreieck zustande kommt, kannst du diesen Wert vernachlässigen. Geometrisch interpretiert heißt das, dass die Seiten  und
und  in dieser Konstruktion niemals gleich lang werden.
in dieser Konstruktion niemals gleich lang werden.
2. Fall: 
Als nächstes überprüfen wir, ob ein  für den Fall
für den Fall  existiert.
existiert.
Auch diese Gleichung hat nur die Lösung  , was wiederum heißt, dass die Seiten
, was wiederum heißt, dass die Seiten  und
und  niemals gleich lang werden.
niemals gleich lang werden.
3. Fall: 
Überprüfe noch den letzten Fall  :
:
Im zweiten Schritt dividieren wir durch  , da für die Lösung
, da für die Lösung  kein Dreieck entsteht.
kein Dreieck entsteht.
Durch Auflösen der Gleichung erhältst du den gesuchten Parameterwert für mit
mit  . Das heißt, für
. Das heißt, für  ist das Dreieck gleichschenklig.
ist das Dreieck gleichschenklig.
Durch Auflösen der Gleichung erhältst du den gesuchten Parameterwert für
c)  Grenzen des Intervalls bestimme, sodass der Mittelwert 2,2 beträgt
Grenzen des Intervalls bestimme, sodass der Mittelwert 2,2 beträgt



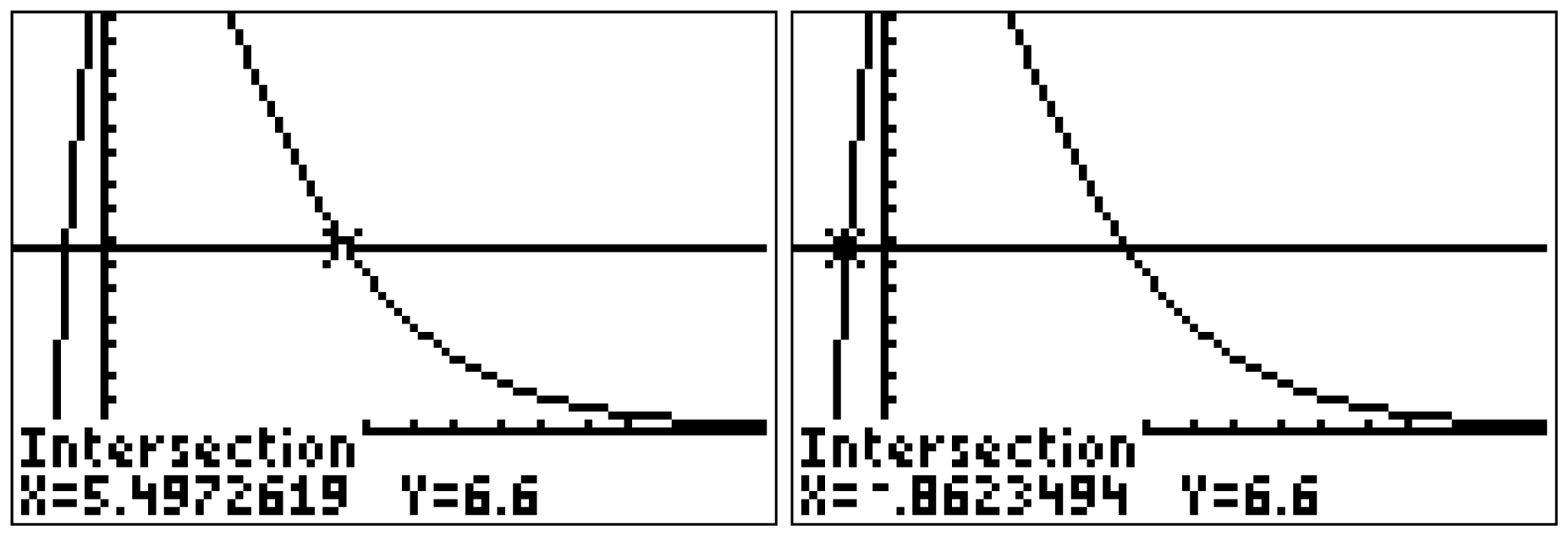
Bestimme ein Intervall der Länge 3, sodass die Funktion  mit dem gegebenen Funktionsterm
mit dem gegebenen Funktionsterm  den Mittelwert 2,2 besitzt.
den Mittelwert 2,2 besitzt.
Den Mittelwert einer Funktion
einer Funktion  auf einem Intervall
auf einem Intervall ![\(\left[a;b\right]\)](https://mathjax.schullv.de/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6?color=5a5a5a) kannst du mit Hilfe der folgenden Formel bestimmen:
kannst du mit Hilfe der folgenden Formel bestimmen:
Den Mittelwert
Um das gesuchte Intervall zu bestimmen, kannst du diese Angaben verwenden:
- Der Mittelwert beträgt laut Aufgabentext
.
- Die Länge des Intervalls soll 3 betragen, das heißt, es muss
bzw.
gelten.
Setze alle bekannten Informationen in die oben angeführte Formel ein und bestimme so das gesuchte Intervall.
Einsetzen aller Angaben liefert dir:
Einsetzen aller Angaben liefert dir:
Um an dieser Stelle die Stammfunktion von  zu erhalten, kannst du partielle Integration verwenden:
zu erhalten, kannst du partielle Integration verwenden:
Wähle in diesem Fall:
Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von  :
:
Setze anschließend noch  und
und  ein:
ein:
Diese Gleichung kannst du graphisch mit Hilfe deines GTR lösen. Gib dazu die rechte und linke Seite der Gleichung als separate Funktionen ein und bestimme deren Schnittpunkt. Den Befehl zur Bestimmung von Schnittpunkten findest du unter
|
menu . |

Der GTR liefert dir Schnittstellen an  und
und  . Das heißt, für das Intervall
. Das heißt, für das Intervall ![\(\left[a;b\right]\)](https://mathjax.schullv.de/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6?color=5a5a5a) mit
mit  und
und  sowie
sowie  und
und  beträgt der Mittelwert der Funktion 2,2.
beträgt der Mittelwert der Funktion 2,2.
Lösung A1.2
Gegeben ist der Funktionsterm einer Funktion  mit:
mit:
Deine Aufgabe ist es, den Parameter  so zu bestimmen, dass die beiden Extrempunkte des Graphen von
so zu bestimmen, dass die beiden Extrempunkte des Graphen von  einen Abstand von 13 besitzen.
einen Abstand von 13 besitzen.
Dazu kannst du wie folgt vorgehen:
Dazu kannst du wie folgt vorgehen:
- Bestimme die Koordinaten der Extrempunkte in Abhängigkeit von
.
- Berechne den Abstand
der Extrempunkte.
- Bestimme
so, dass der Abstand gerade 13 beträgt.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Ermittle anhand diesen Bedingungen die Extremstellen der Funktion  . Hast du diese bestimmt, so kannst du die bestimmten Stellen in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmten Stellen in den Funktionsterm von  einsetzen und erhältst so die zugehörigen Funktionswerte an den Extremstellen.
einsetzen und erhältst so die zugehörigen Funktionswerte an den Extremstellen.
1. Schritt: Extrempunkte bestimmen (Notwendige Bedingung)
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  . Diese erhältst du, indem du die Produktregel anwendest:
. Diese erhältst du, indem du die Produktregel anwendest:
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird.
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird.
Damit hast du zwei potentielle Extremstellen an  und
und  ermittelt und kannst für diese Stellen nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stellen nun das hinreichende Kriterium überprüfen.
2. Schritt: Extrempunkte bestimmen (Hinreichende Bedingung)
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut ableitest:
erneut ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Da in der Aufgabenstellung  vorausgesetzt wird, kann die zweite Ableitungsfunktion nicht gleich Null werden.
vorausgesetzt wird, kann die zweite Ableitungsfunktion nicht gleich Null werden.
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  Extremstellen vorliegen.
Extremstellen vorliegen.
Wegen  kannst du festhalten, dass es sich hierbei um einen Tiefpunkt und handelt. Analog kannst du aussagen, dass wegen
kannst du festhalten, dass es sich hierbei um einen Tiefpunkt und handelt. Analog kannst du aussagen, dass wegen  an der Stelle
an der Stelle  ein Hochpunkt vorliegt.
ein Hochpunkt vorliegt.
3. Schritt: Koordinaten der Extrempunkte angeben
Aus den Berechnungen zuvor weißt du, dass sich an den Stellen  und
und  Extrempunkte befinden. Damit hast du die
Extrempunkte befinden. Damit hast du die  -Koordinate der Extrempunkte ermittelt. Die
-Koordinate der Extrempunkte ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
Das liefert dir, dass der Tiefpunkt die Koordinaten  besitzt.
besitzt.
Das liefert dir, dass der Hochpunkt die Koordinaten  besitzt.
besitzt.
4. Schritt: Abstand der Extrempunkte bestimmen
Den Abstand  zweier Punkte
zweier Punkte  und
und  kannst du über folgenden Zusammenhang bestimmen:
kannst du über folgenden Zusammenhang bestimmen:
Einsetzen der Koordinaten der Extrempunkte  und
und  liefert dir den Abstand mit:
liefert dir den Abstand mit:
Der Abstand der Extrempunkte  und
und  beträgt also
beträgt also  .
.
5. Schritt: Parameterwert für  bestimmen
bestimmen
Damit die beiden Extrempunkte einen Abstand von 13 haben, muss  gelten. Löse diese Gleichung nach
gelten. Löse diese Gleichung nach  auf, um den gesuchten Parameterwert zu erhalten.
auf, um den gesuchten Parameterwert zu erhalten.
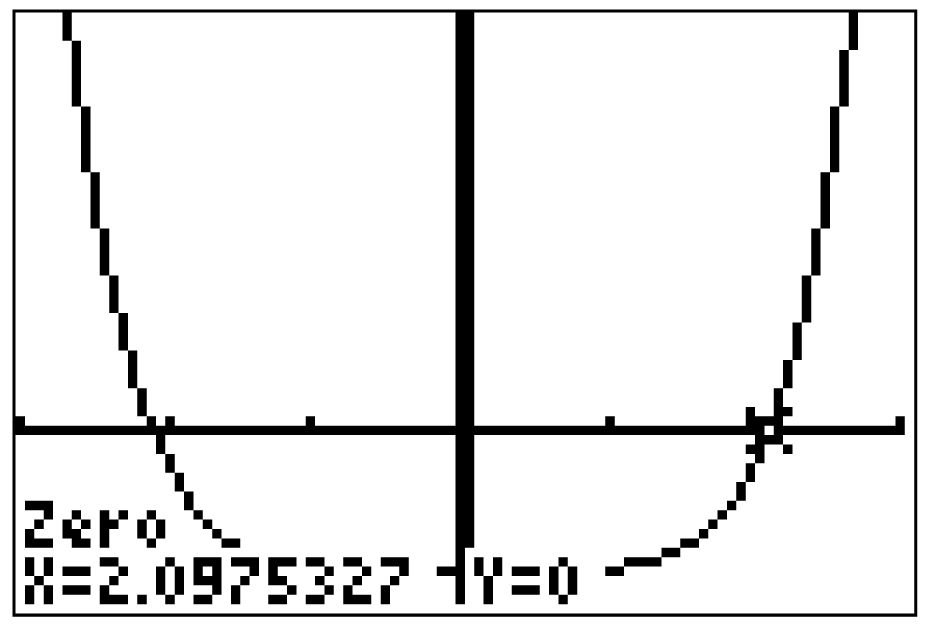
Diese Gleichung kannst du mit Hilfe des GTR graphisch lösen. Interpretiere dazu den Term  als Funktionsterm und untersuche diesen auf Nullstellen.
als Funktionsterm und untersuche diesen auf Nullstellen.
Der GTR liefert dir zwei Resultate:
Der GTR liefert dir zwei Resultate:
Da laut Aufgabenstellung aber  gelten soll, ist
gelten soll, ist  das gesuchte Ergebnis.
das gesuchte Ergebnis.
Es muss gelten, damit der Abstand der beiden Extrempunkte 13 beträgt.
gelten, damit der Abstand der beiden Extrempunkte 13 beträgt.
Es muss
Lösung A1.1
a)  Koordinate des Extrempunktes
Koordinate des Extrempunktes  angeben
angeben

 ist ihr Schaubild. Deine Aufgabe ist es, die Koordinaten des Extrempunktes
ist ihr Schaubild. Deine Aufgabe ist es, die Koordinaten des Extrempunktes  zu bestimmen.
zu bestimmen.
![\(\begin{array}[t]{rll}
f(x)&=& 10 \cdot x \cdot \mathrm{e}^{-0,5 \cdot x}
\end{array}\)](https://mathjax.schullv.de/f22ff724bccd07c4e19dc0f7235300a2d2b557bf2e0140d68063add7c86dde95?color=5a5a5a)


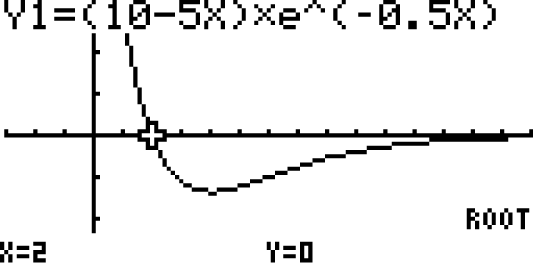
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/1c45a08e96f5b3993031060239011690832e8d84516816cbe4ff65d874b5a5ea?color=5a5a5a)


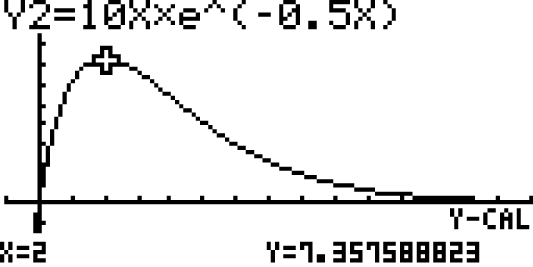
 Koordinate des Wendepunktes
Koordinate des Wendepunktes  angeben
angeben



![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/475d84f4a843c46a0593a5de2d17dbea31311044a6ca5cf4bb14237064473517?color=5a5a5a)

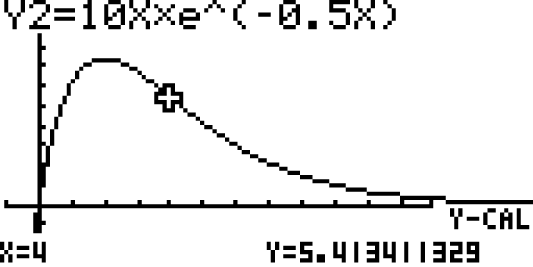
 Gleichung der Asymptote von
Gleichung der Asymptote von  angeben
angeben
 und
und 
 und
und 
 Skizzieren des Schaubildes
Skizzieren des Schaubildes 

 Parameter
Parameter  bestimmen
bestimmen









Gegeben ist der Funktionsterm einer Funktion  mit:
mit:
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  .
.
Diese erhältst du, indem du die Produktregel anwendest:
Diese erhältst du, indem du die Produktregel anwendest:
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
Damit hast du eine potentielle Extremstelle an  ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
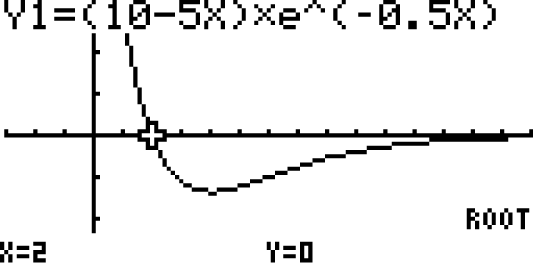
Alternativ bietet es sich auch an, die potentielle Extremstelle mit dem GTR zu bestimmen:
Gib dazu den Term der ersten Ableitungsfunktion ƒ‘ an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
Gib dazu den Term der ersten Ableitungsfunktion ƒ‘ an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
|
G-Solve |
den Befehl zum Bestimmen der Nullstelle aus und bestätige mit Enter.
Der GTR liefert dir eine potentielle Extremstelle an  .
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Extremstelle vorliegt. Wegen
eine Extremstelle vorliegt. Wegen  kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes ermittelt. Die
-Koordinate des Hochpunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
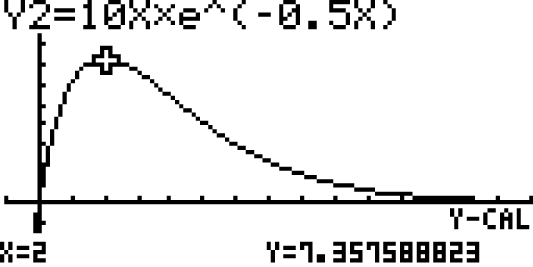
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen.
auch mit Hilfe des GTR bestimmen.
Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle
im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
|
G-Solve |
Die Koordinaten des Extrempunktes  lauten
lauten  .
.
Laut Aufgabenstellung besitzt das Schaubild  einen Wendepunkt. Um dessen Koordinaten angeben zu können, musst du zunächst die Wendestelle
einen Wendepunkt. Um dessen Koordinaten angeben zu können, musst du zunächst die Wendestelle  der Funktion
der Funktion  bestimmen. Für diese Wendestelle müssen folgende Bedingungen erfüllt sein:
bestimmen. Für diese Wendestelle müssen folgende Bedingungen erfüllt sein:
- Notwendige Bedingung:
- Hinreichende Bedingung:
Hast du anschließend  bestimmt, so kannst du die Wendestelle in den Term der Funktion
bestimmt, so kannst du die Wendestelle in den Term der Funktion  einsetzen und so die
einsetzen und so die  -Koordinate des Wendepunktes bestimmen.
-Koordinate des Wendepunktes bestimmen.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Wendestelle der Funktion  zu überprüfen, benötigst du die zweite Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die zweite Ableitungsfunktion der Funktion  . Diese hast du zuvor mit Hilfe der Produktregel bestimmt:
. Diese hast du zuvor mit Hilfe der Produktregel bestimmt:
Für die hinreichende Bedingung muss  gelten:
gelten:
An dieser Stelle kannst du den Satz vom Nullprodukt anwenden. Da der Term  für keinen Wert für
für keinen Wert für  gleich Null werden kann, kannst du diesen vernachlässigen.
gleich Null werden kann, kannst du diesen vernachlässigen.
Damit hast du eine potentielle Wendestelle an  ermittelt.
ermittelt.

Alternativ bietet es sich auch an, die potentielle Wendestelle mit dem GTR zu bestimmen:
Gib dazu den Term der zweiten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
Gib dazu den Term der zweiten Ableitungsfunktion an und lass deren Schaubild im Graph-Modus anzeigen. Wähle dann unter
|
G-Solve |
den Befehl zum Bestimmen der Nullstelle aus und bestätige mit Enter.
Der GTR liefert dir eine potentielle Wendestelle an  .
.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Wendestelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die dritte Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die dritte Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut mit Hilfe der Produktregel ableitest:
erneut mit Hilfe der Produktregel ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  eine Wendestelle liegt.
eine Wendestelle liegt.
3. Schritt: Koordinaten des Wendepunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Wendepunkt befindet. Damit hast du die
ein Wendepunkt befindet. Damit hast du die  -Koordinate des Wendepunktes ermittelt. Die
-Koordinate des Wendepunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
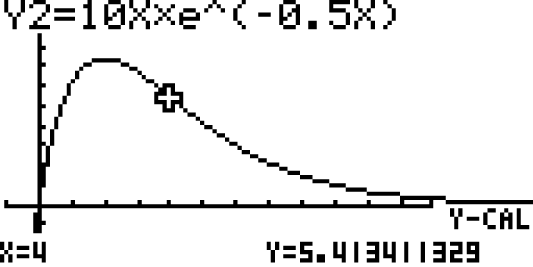
Alternativ kannst du den Funktionswert an der Stelle  auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion
auch mit Hilfe des GTR bestimmen. Gib dazu die Funktion  im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle
im Graph-Modus an und lass deren Graph anzeigen. Den Funktionswert an der besagten Stelle  erhältst du über folgende Befehlsfolge:
erhältst du über folgende Befehlsfolge:
|
G-Solve |
Die Koordinaten des des Wendepunktes  lauten
lauten  .
.

Betrachte das Schaubild der Funktion  in deinem GTR.
in deinem GTR.
Deine Aufgabe ist es, die Gleichung der Asymptote von anzugeben.
anzugeben.
Anhand des Schaubildes (Abbildung links) kannst du bereits vermuten, dass es sich um eine waagrechte Asymptote handelt.
Um die Gleichung der Asymptote zu bestimmen, kannst du die Funktion für
für  und für
und für  untersuchen.
untersuchen.
Deine Aufgabe ist es, die Gleichung der Asymptote von
Anhand des Schaubildes (Abbildung links) kannst du bereits vermuten, dass es sich um eine waagrechte Asymptote handelt.
Um die Gleichung der Asymptote zu bestimmen, kannst du die Funktion
Untersuchen für  :
:
Der Funktionsterm von  ist gegeben durch
ist gegeben durch  .
.
Betrachtest du , so kannst du festhalten, dass gilt:
, so kannst du festhalten, dass gilt:
Betrachtest du
Da der  -Term den dominanten Term darstellt, konvergiert die Funktion
-Term den dominanten Term darstellt, konvergiert die Funktion  für
für  gegen 0.
gegen 0.
Die Gleichung der Asymptote lautet also .
.
Die Gleichung der Asymptote lautet also
Untersuchen für  :
:
Betrachtest du noch  , so kannst du festhalten, dass gilt:
, so kannst du festhalten, dass gilt:
Da auch hier der  -Term den dominanten Term darstellt, der Term durch den Teil
-Term den dominanten Term darstellt, der Term durch den Teil  für
für  aber immer ein negatives Vorzeichen besitzt, strebt die Funktion
aber immer ein negatives Vorzeichen besitzt, strebt die Funktion  für
für  gegen
gegen  . Damit liegt keine weitere Asymptote vor.
. Damit liegt keine weitere Asymptote vor.
Weiterhin verlangt die Aufgabenstellung, das Schaubild  zu skizzieren. Dabei kannst du folgende Angaben verwenden:
zu skizzieren. Dabei kannst du folgende Angaben verwenden:
- Betrachte das Schaubild in deinem GTR, indem du den Graph-Modus auswählst.
- Verwende, dass sich der Hochpunkt an
und der Wendepunkt an
befindet.
- Für
konvergiert die Funktion gegen 0, für
strebt sie gegen
.
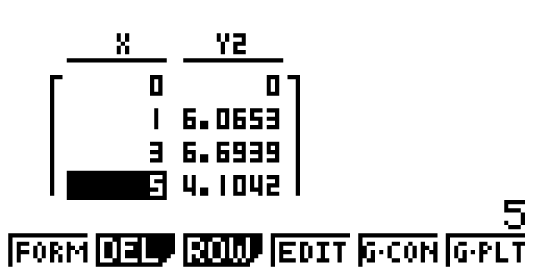
Zusätzlich kannst du dir noch die zugehörige Wertetabelle der Funktion einblenden lassen. Diese findest du im TABLE-Modus unter F6: TABL:

Das Schaubild  sollte dann folgendermaßen aussehen:
sollte dann folgendermaßen aussehen:

b)  Wert für
Wert für  bestimmen, sodass der Flächeninhalt 8 FE beträgt
bestimmen, sodass der Flächeninhalt 8 FE beträgt



![\(\begin{array}[t]{rll}
A(u)&=& \frac{1}{2} \cdot u \cdot 10 \cdot u \cdot \mathrm{e}^{-0,5 \cdot u}& \\[5pt]
&=& 5 \cdot u^2 \cdot \mathrm{e}^{-0,5 \cdot u}
\end{array}\)](https://mathjax.schullv.de/63fcfa2ba41d4ecb0a1c1a82a721514183a9cc5061ccde9a91e74a50c8dd73ce?color=5a5a5a)
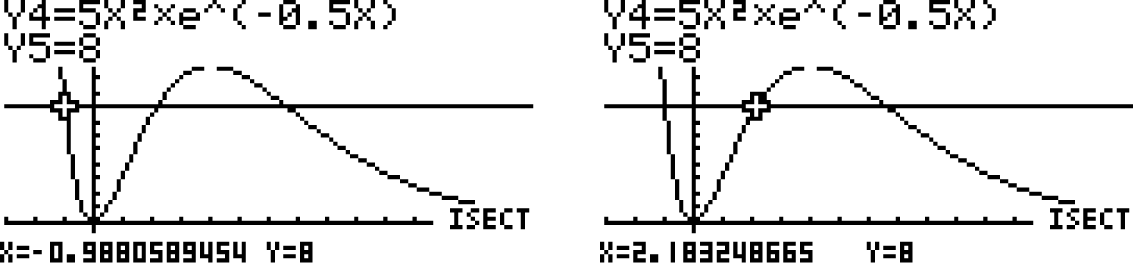
 Wert für
Wert für  bestimmen, sodass das Dreieck gleichschenklig ist
bestimmen, sodass das Dreieck gleichschenklig ist


![\(\begin{array}[t]{rll}
b&=& c & \\[5pt]
10 \cdot u \cdot \mathrm{e}^{-0,5 \cdot u}&=& \sqrt{u^2+ \left(10 \cdot u \cdot \mathrm{e}^{-0,5 \cdot u}\right)^2}&\quad \scriptsize \mid\; (\,)^2 \\[5pt]
100 \cdot u^2 \cdot \mathrm{e}^{-u}&=& u^2+ 100 \cdot u^2 \cdot \mathrm{e}^{-u}&\quad \scriptsize \mid\; -100 \cdot u^2 \cdot \mathrm{e}^{-u} \\[5pt]
0&=& u^2
\end{array}\)](https://mathjax.schullv.de/32946da8f481912752d06e5eaf4be091d4eaadc45695f86f56407e90546ab1b3?color=5a5a5a)

Gegeben sind die Punkte  ,
,  und
und  . Sie stellen die Eckpunkte eines Dreiecks dar.
. Sie stellen die Eckpunkte eines Dreiecks dar.
Deine Aufgabe ist es, einen Wert für so zu bestimmen, dass der Flächeninhalt des Dreieck 8 FE beträgt.
so zu bestimmen, dass der Flächeninhalt des Dreieck 8 FE beträgt.
Deine Aufgabe ist es, einen Wert für

Der Flächeninhalt  eines Dreiecks berechnet sich allgemein über folgenden Zusammenhang:
eines Dreiecks berechnet sich allgemein über folgenden Zusammenhang:
Dabei stellt  die Länge der Grundseite und
die Länge der Grundseite und  die Länge der Höhe dar.
die Länge der Höhe dar.
Um einen passenden Wert für zu ermitteln, kannst du wie folgt vorgehen:
zu ermitteln, kannst du wie folgt vorgehen:
Um einen passenden Wert für
- Stelle die Flächenfunktion in Abhängigkeit vom Parameter
auf.
- Setze den resultierenden Term mit 8 gleich und löse nach
auf, um den gesuchten Wert zu erhalten.
Den zweiten Schritt kannst du mit Hilfe deines GTR durchführen.
1. Schritt: Flächenfunktion aufstellen
Anhand der Abbildung kannst du erkennen, dass die Grundseite dem Wert  und die Höhe dem Funktionswert
und die Höhe dem Funktionswert  entspricht. Dadurch erhältst du folgende von
entspricht. Dadurch erhältst du folgende von  abhängige Flächenfunktion
abhängige Flächenfunktion  :
:
Setze den Funktionsterm von  ein, um den vollständigen Term er Flächenfunktion
ein, um den vollständigen Term er Flächenfunktion  zu erhalten:
zu erhalten:
2. Schritt: Wert für Parameter  ermitteln
ermitteln
Um einen passenden Wert für  zu erhalten, sodass der Flächeninhalt 8 FE beträgt, kannst du den aufgestellten Term der Flächenfunktion mit 8 gleichsetzen und nach
zu erhalten, sodass der Flächeninhalt 8 FE beträgt, kannst du den aufgestellten Term der Flächenfunktion mit 8 gleichsetzen und nach  auflösen. Da dieser Weg rechnerisch sehr aufwendig ist, wählen wir die graphische Lösung des Problems mit Hilfe des GTR:
auflösen. Da dieser Weg rechnerisch sehr aufwendig ist, wählen wir die graphische Lösung des Problems mit Hilfe des GTR:
- Gib den Funktionsterm
im GTR ein.
- Gib weiterhin eine Gerade mit der Gleichung y = 8 an und lass beide im Graph-Modus anzeigen.
- Bestimme die Schnittstelle der beiden Schaubilder. Diese entspricht gerade dem gesuchten Wert für
.


Der GTR liefert dir drei verschiedene Werte für  , sodass der Flächeninhalt 8 FE beträgt.
, sodass der Flächeninhalt 8 FE beträgt.
Da aber laut Aufgabenstellung gelten soll, kannst du das Resultat
gelten soll, kannst du das Resultat  vernachlässigen.
vernachlässigen.
Da aber laut Aufgabenstellung
Damit hast du zwei passende Werte für  ermittelt mit
ermittelt mit
,
.

Damit das Dreieck gleichschenklig ist, muss einer der folgenden Fälle eintreten:
oder
oder
.
Gib dazu zunächst die Länge der Seiten  ,
,  und
und  in Abhängigkeit von
in Abhängigkeit von  an und setze diese gleich, um so einen passenden Parameterwert für
an und setze diese gleich, um so einen passenden Parameterwert für  zu ermitteln.
zu ermitteln.
1. Schritt: Länge der Seiten in Abhängigkeit von  angeben
angeben
- Die Seitenlänge
entspricht dem Abstand vom Ursprung
zum Punkt
. Dieser Abstand ist gerade gleich
.
- Die Seitenlänge
stellt den Abstand zwischen den Punkten
und
dar. Da diese die gleiche
-Koordinate haben, besitzen sie einen Abstand von
.
berechnet sich mit Hilfe des Satzes von Pythagoras:
2. Schritt: Seitenlängen gleichsetzen, um  zu bestimmen
zu bestimmen
Damit das Dreieck gleichschenklig ist, können die oben genannten drei Fälle  ,
,  oder
oder  eintreten. Wir überprüfen zunächst, ob für den Fall
eintreten. Wir überprüfen zunächst, ob für den Fall  ein
ein  existiert:
existiert:
1. Fall: 
Mit dem Satz vom Nullprodukt folgt, dass die Gleichung nur für  gelöst werden kann. Da aber für
gelöst werden kann. Da aber für  kein Dreieck zustande kommt, kannst du diesen Wert vernachlässigen. Geometrisch interpretiert heißt das, dass die Seiten
kein Dreieck zustande kommt, kannst du diesen Wert vernachlässigen. Geometrisch interpretiert heißt das, dass die Seiten  und
und  in dieser Konstruktion niemals gleich lang werden.
in dieser Konstruktion niemals gleich lang werden.
2. Fall: 
Als nächstes überprüfen wir, ob ein  für den Fall
für den Fall  existiert.
existiert.
Auch diese Gleichung hat nur die Lösung  , was wiederum heißt, dass die Seiten
, was wiederum heißt, dass die Seiten  und
und  niemals gleich lang werden.
niemals gleich lang werden.
3. Fall: 
Überprüfe noch den letzten Fall  :
:
Im zweiten Schritt dividieren wir durch  , da für die Lösung
, da für die Lösung  kein Dreieck entsteht.
kein Dreieck entsteht.
Durch Auflösen der Gleichung erhältst du den gesuchten Parameterwert für mit
mit  . Das heißt, für
. Das heißt, für  ist das Dreieck gleichschenklig.
ist das Dreieck gleichschenklig.
Durch Auflösen der Gleichung erhältst du den gesuchten Parameterwert für
c)  Grenzen des Intervalls bestimme, sodass der Mittelwert 2,2 beträgt
Grenzen des Intervalls bestimme, sodass der Mittelwert 2,2 beträgt



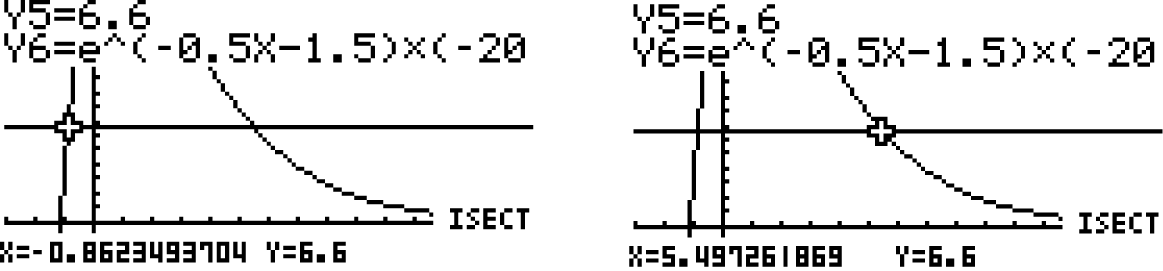
Bestimme ein Intervall der Länge 3, sodass die Funktion  mit dem gegebenen Funktionsterm
mit dem gegebenen Funktionsterm  den Mittelwert 2,2 besitzt.
den Mittelwert 2,2 besitzt.
Den Mittelwert einer Funktion
einer Funktion  auf einem Intervall
auf einem Intervall ![\(\left[a;b\right]\)](https://mathjax.schullv.de/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6?color=5a5a5a) kannst du mit Hilfe der folgenden Formel bestimmen:
kannst du mit Hilfe der folgenden Formel bestimmen:
Den Mittelwert
Um das gesuchte Intervall zu bestimmen, kannst du diese Angaben verwenden:
- Der Mittelwert beträgt laut Aufgabentext
.
- Die Länge des Intervalls soll 3 betragen, das heißt, es muss
bzw.
gelten.
Setze alle bekannten Informationen in die oben angeführte Formel ein und bestimme so das gesuchte Intervall.
Einsetzen aller Angaben liefert dir:
Einsetzen aller Angaben liefert dir:
Um an dieser Stelle die Stammfunktion von  zu erhalten, kannst du partielle Integration verwenden:
zu erhalten, kannst du partielle Integration verwenden:
Wähle in diesem Fall:
Einsetzen in die oben angeführte Formel liefert dir das gesuchte Integral von  :
:
Setze anschließend noch  und
und  ein:
ein:
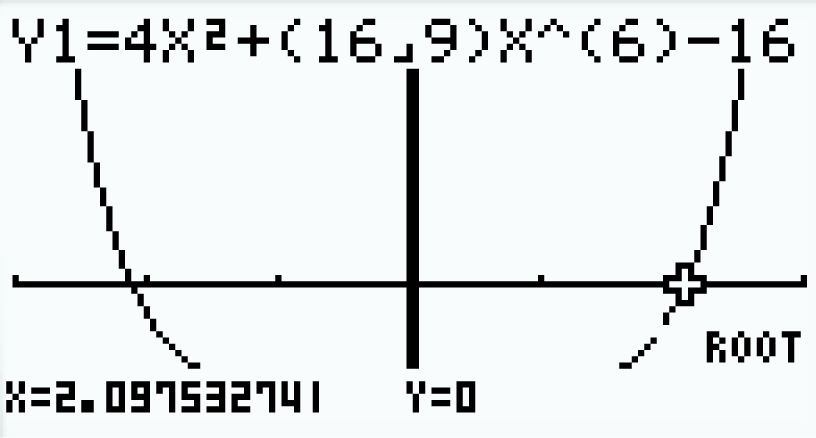
Diese Gleichung kannst du graphisch mit Hilfe deines GTR lösen. Gib dazu die rechte und linke Seite der Gleichung als separate Funktionen ein und bestimme deren Schnittpunkt. Den Befehl zur Bestimmung von Schnittpunkten findest du unter
|
G-Solve . |
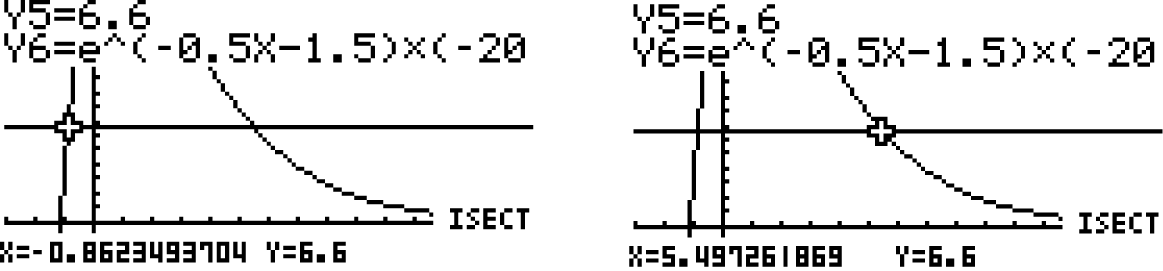
Der GTR liefert dir Schnittstellen an  und
und  . Das heißt, für das Intervall
. Das heißt, für das Intervall ![\(\left[a;b\right]\)](https://mathjax.schullv.de/17818209ab83b5875fd5fb4cb16a774cda3e6470ce6bae88138263a93b57c7d6?color=5a5a5a) mit
mit  und
und  sowie
sowie  und
und  beträgt der Mittelwert der Funktion 2,2.
beträgt der Mittelwert der Funktion 2,2.
Lösung A1.2
Gegeben ist der Funktionsterm einer Funktion  mit:
mit:
Deine Aufgabe ist es, den Parameter  so zu bestimmen, dass die beiden Extrempunkte des Graphen von
so zu bestimmen, dass die beiden Extrempunkte des Graphen von  einen Abstand von 13 besitzen.
einen Abstand von 13 besitzen.
Dazu kannst du wie folgt vorgehen:
Dazu kannst du wie folgt vorgehen:
- Bestimme die Koordinaten der Extrempunkte in Abhängigkeit von
.
- Berechne den Abstand
der Extrempunkte.
- Bestimme
so, dass der Abstand gerade 13 beträgt.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Ermittle anhand diesen Bedingungen die Extremstellen der Funktion  . Hast du diese bestimmt, so kannst du die bestimmten Stellen in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmten Stellen in den Funktionsterm von  einsetzen und erhältst so die zugehörigen Funktionswerte an den Extremstellen.
einsetzen und erhältst so die zugehörigen Funktionswerte an den Extremstellen.
1. Schritt: Extrempunkte bestimmen (Notwendige Bedingung)
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  . Diese erhältst du, indem du die Produktregel anwendest:
. Diese erhältst du, indem du die Produktregel anwendest:
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze also den Funktionsterm der ersten Ableitung
gelten. Setze also den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird.
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird.
Damit hast du zwei potentielle Extremstellen an  und
und  ermittelt und kannst für diese Stellen nun das hinreichende Kriterium überprüfen.
ermittelt und kannst für diese Stellen nun das hinreichende Kriterium überprüfen.
2. Schritt: Extrempunkte bestimmen (Hinreichende Bedingung)
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut ableitest:
erneut ableitest:
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
Da in der Aufgabenstellung  vorausgesetzt wird, kann die zweite Ableitungsfunktion nicht gleich Null werden.
vorausgesetzt wird, kann die zweite Ableitungsfunktion nicht gleich Null werden.
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist und damit, dass an  Extremstellen vorliegen.
Extremstellen vorliegen.
Wegen  kannst du festhalten, dass es sich hierbei um einen Tiefpunkt und handelt. Analog kannst du aussagen, dass wegen
kannst du festhalten, dass es sich hierbei um einen Tiefpunkt und handelt. Analog kannst du aussagen, dass wegen  an der Stelle
an der Stelle  ein Hochpunkt vorliegt.
ein Hochpunkt vorliegt.
3. Schritt: Koordinaten der Extrempunkte angeben
Aus den Berechnungen zuvor weißt du, dass sich an den Stellen  und
und  Extrempunkte befinden. Damit hast du die
Extrempunkte befinden. Damit hast du die  -Koordinate der Extrempunkte ermittelt. Die
-Koordinate der Extrempunkte ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
Das liefert dir, dass der Tiefpunkt die Koordinaten  besitzt.
besitzt.
Das liefert dir, dass der Hochpunkt die Koordinaten  besitzt.
besitzt.
4. Schritt: Abstand der Extrempunkte bestimmen
Den Abstand  zweier Punkte
zweier Punkte  und
und  kannst du über folgenden Zusammenhang bestimmen:
kannst du über folgenden Zusammenhang bestimmen:
Einsetzen der Koordinaten der Extrempunkte  und
und  liefert dir den Abstand mit:
liefert dir den Abstand mit:
Der Abstand der Extrempunkte  und
und  beträgt also
beträgt also  .
.
5. Schritt: Parameterwert für  bestimmen
bestimmen
Damit die beiden Extrempunkte einen Abstand von 13 haben, muss  gelten. Löse diese Gleichung nach
gelten. Löse diese Gleichung nach  auf, um den gesuchten Parameterwert zu erhalten.
auf, um den gesuchten Parameterwert zu erhalten.

Diese Gleichung kannst du mit Hilfe des GTR graphisch lösen. Interpretiere dazu den Term  als Funktionsterm und untersuche diesen auf Nullstellen.
als Funktionsterm und untersuche diesen auf Nullstellen.
Der GTR liefert dir zwei Resultate:
Der GTR liefert dir zwei Resultate:
Da laut Aufgabenstellung aber  gelten soll, ist
gelten soll, ist  das gesuchte Ergebnis.
das gesuchte Ergebnis.
Es muss gelten, damit der Abstand der beiden Extrempunkte 13 beträgt.
gelten, damit der Abstand der beiden Extrempunkte 13 beträgt.
Es muss