Wahlteil B1

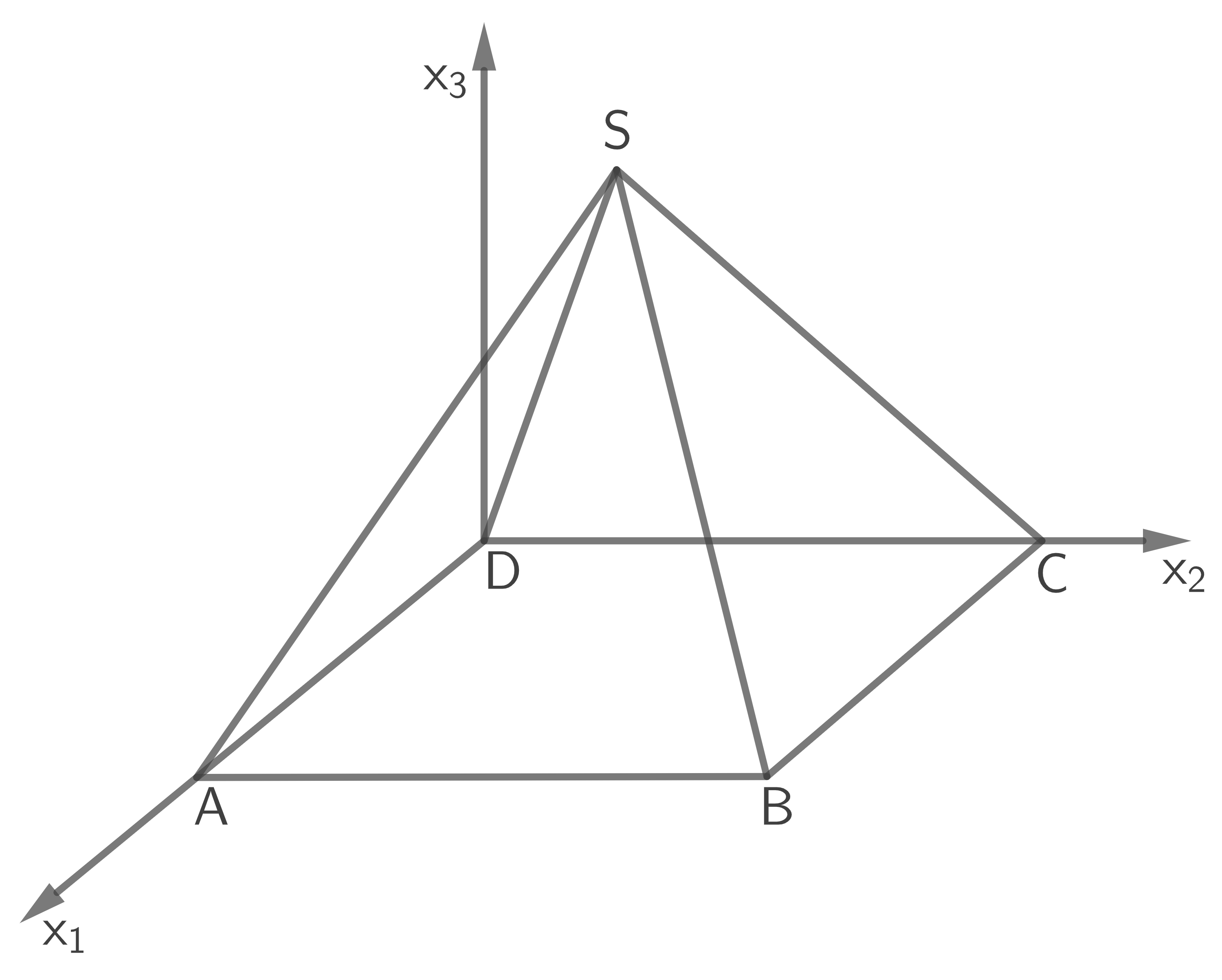
Ein Ausstellungsraum hat die Form einer geraden Pyramide mit quadratischer Grundfläche. Die Eckpunkte des Bodens können in einem kartesischen Koordinatensystem modellhaft durch die Punkte $A\,(18 \mid 0 \mid 0)$ , $B\,(18 \mid 18 \mid 0)$ , $C\,(0\mid 18\mid 0)$ und $D\,(0\mid 0\mid 0)$ dargestellt werden (siehe unten stehende Abbildung). Die Spitze des Raumes wird durch den Punkt $S\,(9\mid 9\mid 12)$ beschrieben, die rechte Seitenwand durch das gleichschenklige Dreieck $BCS$ (alle Koordinatenangaben in Meter).

Geometrische Darstellung eines dreidimensionalen Koordinatensystems mit Punkten A, B, C, D und S.

Berechne die Größe des Winkels zwischen den beiden Kanten, die durch die Strecken $\overline{BC}$ und $\overline{BS}$ beschrieben werden.

Ermittle eine Koordinatengleichung der Ebene $E$ , in der das Dreieck $BCS$ liegt.

Bestimme den Flächeninhalt der rechten Seitenwand.
(Teilergebnis: $E = 4x_2+3x_3=72$ )

(5 VP)

Eine punktförmige Lampe befindet sich am unteren Ende einer fünf Meter langen Stange, die von der Raumspitze ausgeht und senkrecht nach unten hängt.

Die Stange mit der Lampe kann in eine Pendelbewegung versetzt werden.
Diese Pendelbewegung verläuft im Modell in einer Ebene parallel zur $x_2x_3$ -Ebene.
Wenn die Lampe zu stark schwingt, dann trifft sie die rechte Seitenwand. Der Auftreffpunkt wird im Modell durch den Punkt $P$ beschrieben.

Berechne die Koordinaten von $P$ .

(2 VP)

Im Rahmen einer Kunstausstellung wurde ein drei Meter langer Stab senkrecht zum Boden angebracht, der im Modell durch die Strecke $\overline{FG}$ mit $F\,(11\mid 15 \mid 0)$ beschrieben wird. Befindet sich die Lampe in der Position, die durch $L\,(9\mid 9\mid 7)$ beschrieben wird, so wirft der Stab einen Schatten, dessen Endpunkt auf der rechten Seitenwand durch $G^*$ beschrieben wird.

Berechne die Koordinaten des Punktes $G^*$ .

Beschreibe ein Verfahren, mit dem man die Gesamtlänge des betrachteten Schattens berechnen kann.

(3 VP)

Winkel berechnen
Aufstellen der Richtungsvektoren:

$\overrightarrow{BC} = \pmatrix {0\\18\\0} -\pmatrix{18\\18\\0} = \pmatrix{-18\\0\\0}$

$\overrightarrow{BS} = \pmatrix{9\\9\\12} - \pmatrix{18\\18\\0} = \pmatrix {-9\\-9\\12}$

Vollständigen Rechenweg anzeigen

$\alpha \approx 59,04^\circ$

Ebenengleichung in Koordinatenform ermitteln
$\overrightarrow{BC}$ und $\overrightarrow{BS}$ sind Vielfache der Spannvektoren von $E$ . Folglich sind $\overrightarrow{u}=\pmatrix{1\\0\\0}$ und $\overrightarrow{v}=\pmatrix{3\\3\\-4}$ Spannvektoren von $E$ .
Der Normalenvektor der Ebene $E$ wird mit dem Kreuzprodukt der Spannvektoren berechnet:

$\overrightarrow{n}=\pmatrix{1\\0\\0} \times \pmatrix{3\\3\\-4} = \pmatrix{0\\4\\3}$ .

Die Ebenengleichung lässt sich damit bestimmen mit $4x_2 +3x_3 =c$ . Um $c$ zu bestimmen, werden die Koordinaten eines Punktes (z.B. $C(0\mid 18\mid 0$ )) in die Gleichung eingesetzt:

$4\cdot 18+0=c,$ also $c=72$

Daraus ergibt sich die Koordinatengleichung $E: 4x_2 +3x_3 =72$ .

Flächeninhalt bestimmen
Es handelt sich um ein Dreieck, dessen Flächeninhalt sich über die Grundseite $\overline{BC}$ und der Höhe des Dreiecks berechnet. dieser Seite. Die Länge der Höhe entspricht dabei dem Abstand der Spitze $S$ der Pyramide zum Mittelpunkt der Strecke $\overline{BC}$ .
Der Flächeninhalt berechnet sich über $A= \dfrac{1}{2} \cdot \left| \overrightarrow{BC} \right| \cdot \left | \overrightarrow{M_{BC}S}\right | .$

$\overrightarrow{M_{BC}} =\pmatrix {18\\18\\0} \cdot \dfrac{1}{2} \cdot \pmatrix{1\\0\\0} =\pmatrix{9\\18\\0}$

$\left|\overrightarrow{BC}\right|=\left|\pmatrix{-18\\0\\0}\right|=\sqrt{(-18)^2+0^2+0^2}=18$

$\left|\overrightarrow{M_{BC}S}\right|=\left|\pmatrix{9\\9\\12}-\pmatrix{9\\18\\0}\right|$ $=\left|\pmatrix{0\\-9\\12}\right|$ $=\sqrt{0^2+(-9)^2+12^2}=15$

$A= \dfrac{1}{2} \cdot \left | \overrightarrow{BC} \right | \cdot \left | \overrightarrow{M_{BC}S}\right | = \dfrac{1}{2} \cdot 18 \cdot 15 = 135$ .

Der Flächeninhalt der Seitenwand beträgt $135\, \text{m}^2$ .

Die Lampe trifft im Punkt $P$ auf die Seitenwand. Die Lampe hat einen Abstand von fünf Metern zu $S$ in Richtung $M_{BC}.$

$\begin{array}[t]{rll} \overrightarrow{OP} &=&\overrightarrow{OS}+ 5 \cdot \dfrac{\overrightarrow{SM_{BC}}}{\left | \overrightarrow{SM_{BC}} \right | }\\[5pt] &=&\pmatrix{9\\9\\12} +5 \cdot \dfrac{\pmatrix{0\\9\\-12}}{\sqrt{0^2+9^2+(-12)^2}}\\ &=&\pmatrix{9\\9\\12}+\dfrac{1}{3}\cdot\pmatrix{0\\9\\-12}=\pmatrix{9\\12\\8} \end{array}$

$P(9 \mid 12 \mid 8)$

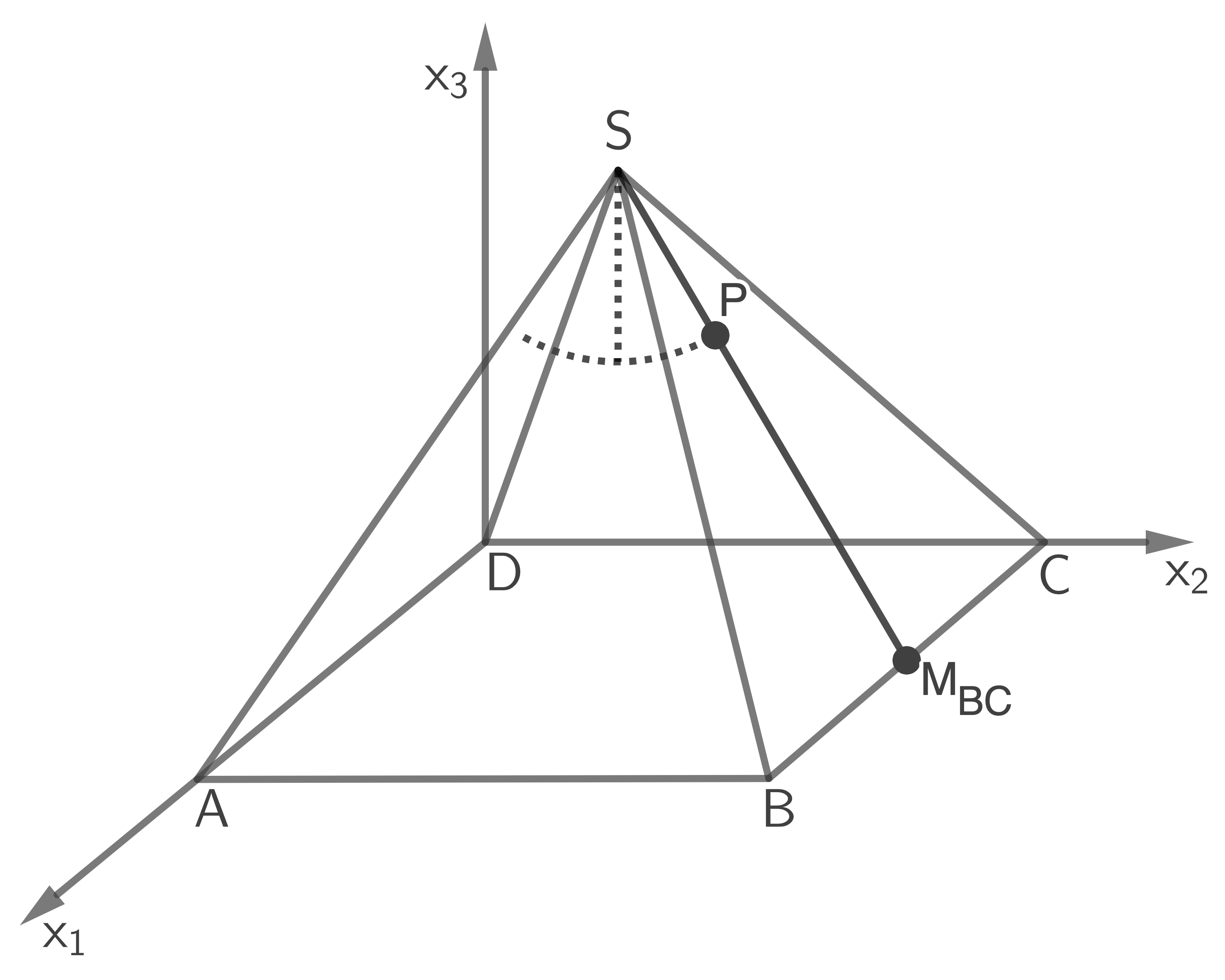
Dreidimensionales Diagramm mit Punkten und Achsenbeschriftungen x1, x2, x3 sowie den Punkten S, P, D, A, B, C, MBC.

Skizze nicht maßstäblich

Koordinaten von $G^*$ berechnen

$G^*$ ist der Schnittpunkt des von $L$ ausgehenden Lichtstrahls, der auf der Geraden $g:\overrightarrow{x}=\overrightarrow{OL}+r\cdot\overrightarrow{LG}$ liegt, mit der Ebene $E,$ in der die rechte Seitenwand liegt.

Der Stab ist $3\,\text{m}$ lang und steht senkrecht zum Boden, das heißt die Koordinaten von $G$ sind $(11 \mid 15 \mid 3)$ .

$g: \overrightarrow{x}= \pmatrix{9\\9\\7} +r \cdot \pmatrix{2\\6\\-4}$

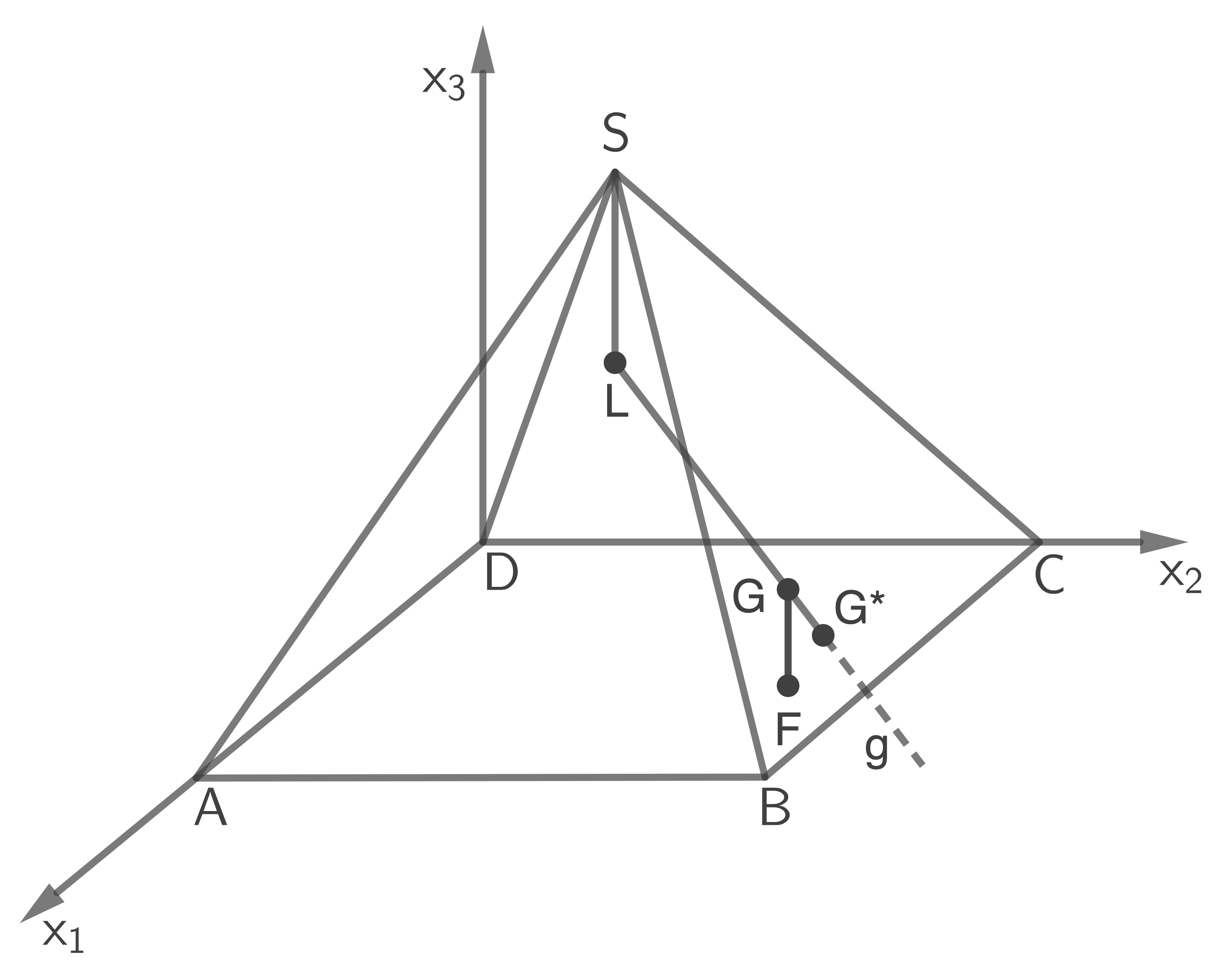Geometrische Darstellung mit Punkten und Linien im Raum, beschriftet mit S, L, D, F, G und den Achsen x1, x2, x3.

Skizze nicht maßstäblich

Schnittpunkt von $g$ mit $E$ berechnen: Die Ebenengleichung von $E$ ist aus Teilaufgabe a) mit $E:4x_2+3x_3=72$ bekannt. Aus $g$ folgt: $x_1= 9+ 2r$ , $x_2= 9+ 6r$ und $x_3= 7-4r$

Diese Koordinaten werden eingesetzt in die Koordinatengleichung:

$\begin{array}[t]{rll} 4(9+6r) +3(7-4r)&=&72 \quad \scriptsize \\[5pt] 36+24r +21-12r&=&72 \quad \scriptsize \mid\;-57 \\[5pt] 12r&=&15 \quad \scriptsize \mid\;:12 \\[5pt] r&=&\dfrac{5}{4} \end{array}$

$r$ in $g$ eingesetzt ergibt $G^*:$ $\overrightarrow{OG^*}= \pmatrix{9\\9\\7} +\dfrac{5}{4} \cdot \pmatrix{2\\6\\-4} = \pmatrix{11,5\\16,5\\2}$ .

Die Koordinaten von $G^*$ sind demnach $(11,5 \mid 16,5 \mid 2).$

Verfahren beschreiben

Der Schatten verläuft auf dem Boden über die Seitenfläche und endet dort. Um die Länge zu bestimmen, kann eine Gleichung der Ebene $H$ aufgestellt werden, welche die Punkte $L,$ $F$ und $G$ enthält. Der Schnittpunkt $T$ ist dann der Punkt, in dem sich $H$ und $\overline{BC}$ schneiden.
Die Gesamtlänge des Schattens kann dann mit $\left | \overrightarrow{FT} \right| + \left | \overrightarrow{TG^*} \right |$ berechnet werden.

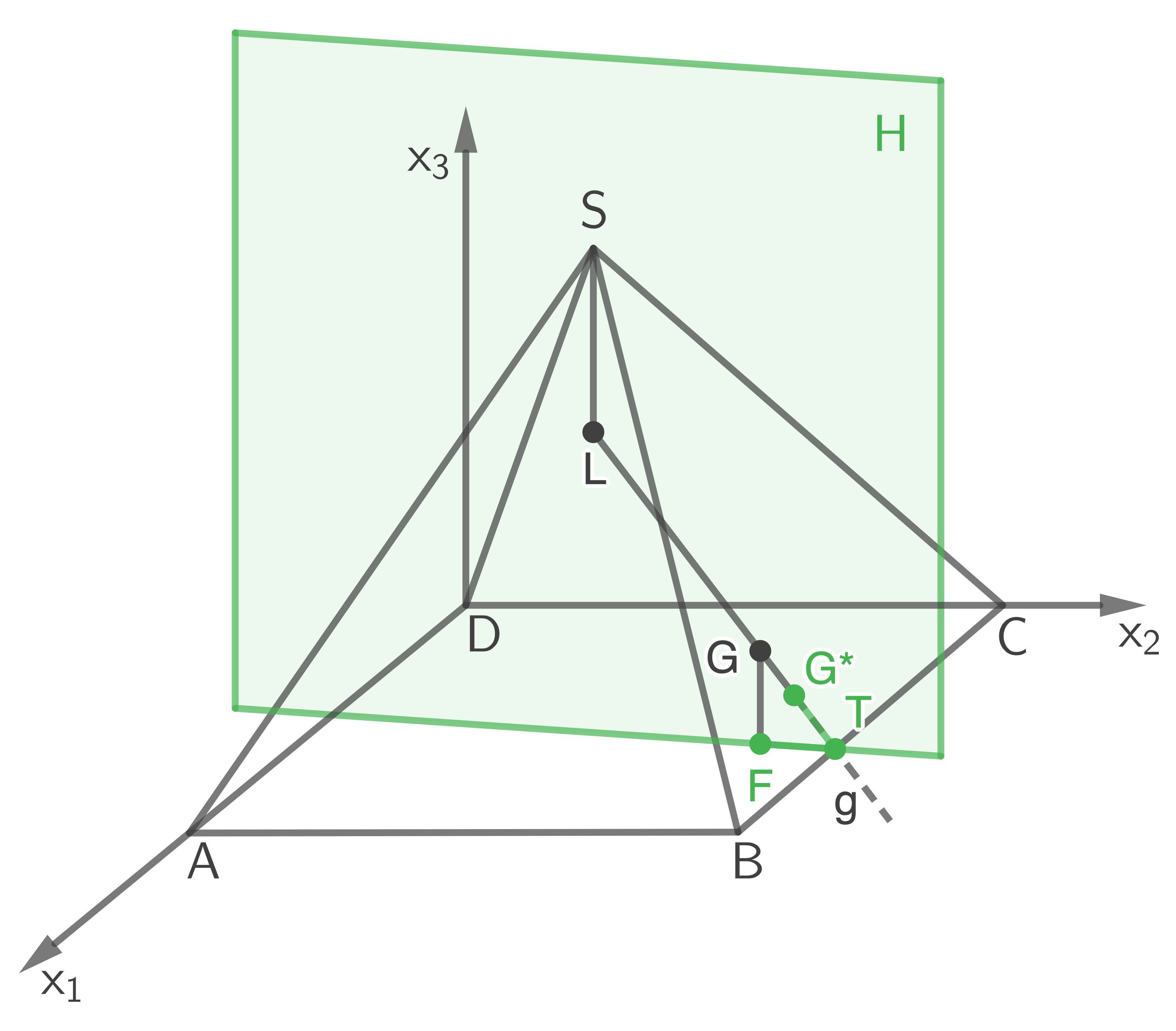
Geometrische Darstellung eines dreidimensionalen Raums mit Punkten und Linien.

Skizze nicht maßstäblich