Wahlteil C2

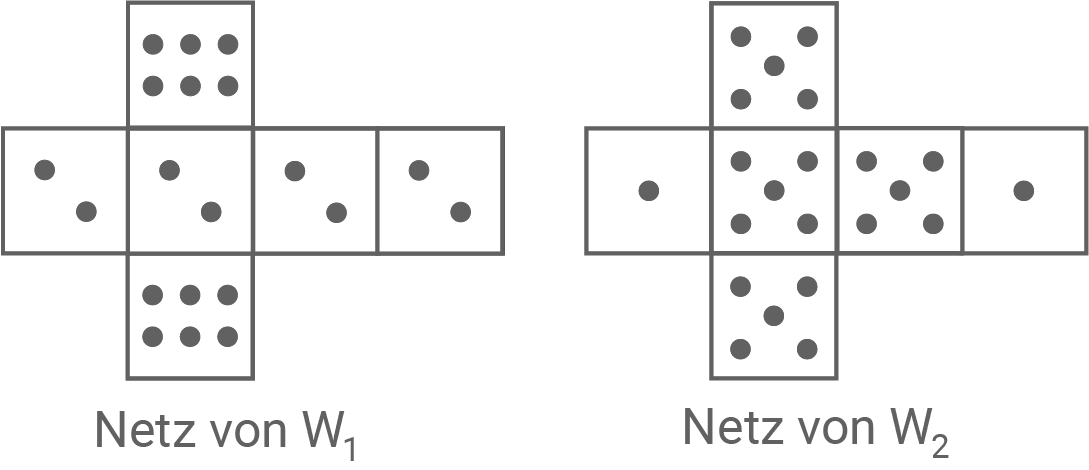
Michael und Torsten spielen mit den beiden Würfeln, deren Netze abgebildet sind, folgendes Spiel:

Michael würfelt mit dem Würfel $W_1,$ Torsten würfelt mit dem Würfel $W_2.$

Der Spieler mit der höheren Augenzahl gewinnt.

Wuerfelnetz Stochastik BW Mathe Abi 2023

Gib alle möglichen Würfelergebnisse an, bei denen Michael das Spiel gewinnt.

(1 VP)

Begründe, dass Michaels Gewinnwahrscheinlichkeit $\dfrac{5}{9}$ beträgt.

(1 VP)

Michael und Torsten spielen 30 Spiele.

Berechne die Wahrscheinlichkeit der folgenden Ereignisse:

$A:$ „Michael gewinnt mindestens 13, aber höchstens 20 Spiele.“

(1 VP)

$B:$ „Torsten gewinnt mehr Spiele als Michael.“

(1 VP)

Es werden $n$ Spiele gespielt. Die Wahrscheinlichkeit dafür, dass Michael dabei nur das letzte Spiel gewinnt, soll weniger als $5 \,\%$ betragen.

Bestimme den kleinstmöglichen Wert von $n.$

(2 VP)

Das Spiel wird folgendermaßen verändert: Vor dem Würfeln wird ein Glücksrad mit einem grünen und einem roten Sektor einmal gedreht. Wenn dabei grün erscheint, dann behalten Michael und Torsten ihre Würfel; erscheint rot, dann tauschen sie die Würfel.

Die Wahrscheinlichkeit dafür, dass Michael bei diesem Spiel eine höhere Zahl als Torsten würfelt, beträgt $\dfrac{7}{15}.$

Bestimme für den grünen Sektor die Größe des Mittelpunktswinkels.

(2,5 VP)

Torsten hat den Verdacht, dass beim Würfel $W_2$ die Wahrscheinlichkeit für die Augenzahl 5 nicht $\dfrac{2}{3}$ beträgt. Daher wird ein einseitiger Hypothesentest mit 500 Würfen auf dem Signifikanzniveau $s$ durchgeführt.

Dabei ergibt sich die Entscheidungsregel, dass die Nullhypothese genau dann abgelehnt wird, wenn weniger als 318-mal die Augenzahl 5 erzielt wird.

Formuliere die zugehörige Nullhypothese.

(0,5 VP)

Bestimme alle ganzzahligen Prozentwerte, die für $s$ in Frage kommen.

(1,5 VP)

Formuliere den Fehler zweiter Art im Sachzusammenhang.

(1 VP)

Bestimme die Wahrscheinlichkeit für den Fehler zweiter Art unter der Annahme, dass beim Würfel $W_2$ die Augenzahl 5 mit einer Wahrscheinlichkeit von $60 \,\%$ erzielt wird.

(1 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Mögliche Ereignisse angeben

$(2;1), \;(6;1), \; (6;5)$

Gewinnwahrscheinlichkeit begründen

$\begin{array}[t]{rll} P&=& P(2;1)+P(6;1)+P(6;5)& \\[5pt] &=& \dfrac{4}{6}\cdot \dfrac{2}{6}+\dfrac{2}{6}\cdot \dfrac{2}{6}+\dfrac{2}{6}\cdot \dfrac{4}{6}& \\[5pt] &=& \dfrac{5}{9}& \\[5pt] \end{array}$

Die Zufallsgröße $X$ beschreibt die Anzahl der Spiele, die Michael gewinnt, und ist $B_{30;\frac{5}{9}}$ -verteilt.

Ereignis $A$

$\begin{array}[t]{rll} P(A)&=& P(13 \leq X \leq 20)& \\[5pt] &=& P(X\leq20)-P(X\leq 12)& \\[5pt] &\approx& 0.922-0.063& \\[5pt] &=& 85,9 \,\% \end{array}$

Ereignis $B$

$\begin{array}[t]{rll} P(B)&=& P(X\leq14)& \\[5pt] &\approx& 0,213 & \\[5pt] &=& 21,3 \,\% \end{array}$

Es soll gelten:

$\left(\dfrac{4}{9}\right)^{n-1}\cdot \dfrac{5}{9}\lt 0,05$

Systematisches Ausprobieren liefert folgende Werte:

$\left(\dfrac{4}{9}\right)^{3-1}\cdot \dfrac{5}{9}\approx 0,11$

$\left(\dfrac{4}{9}\right)^{4-1}\cdot \dfrac{5}{9}\approx 0,049$

Der kleinstmögliche Wert von $n$ ist somit 4. Es müssen also mindestens 4 Spiele gespielt werden.

$p_G$ entspricht der Wahrscheinlichkeit, dass der grüne Sektor erscheint.

Die Wahrscheinlichkeit dafür, dass Michael gewinnt, kann durch folgende Gleichung berechnet werden:

Rechenweg anzeigen

$p_g = \dfrac{1}{5}$

Die Größe des Mittelpunktswinkels des grünen Sektors folgt also mit:

$360^{\circ}\cdot \dfrac{1}{5}=72^{\circ}$

Nullhypothese formulieren

$H_0:\;$ „Die Wahrscheinlichkeit dafür, eine 5 zu würfeln, beträgt mindestens $\dfrac{2}{3}.$ "

Prozentwerte bestimmen

$Y$ beschreibt die Anzahl der Würfe, bei denen eine 5 erzielt wird und ist $B_{500;\frac{2}{3}}$ -verteilt.

$P(Y\leq 317)\approx 0,0673$

$P(Y\leq 318) \approx 0,0804$

Somit sind $7\,\%$ und $8\,\%$ mögliche ganzzahlige Prozentwerte, die für $s$ in Frage kommen.

Fehler zweiter Art formulieren

Obwohl die Wahrscheinlichkeit dafür, eine 5 zu würfeln, kleiner als $\dfrac{2}{3}$ ist, wird die Nullhypothese nicht abgelehnt.

Wahrscheinlichkeit bestimmen

$Z$ beschreibt die Anzahl der Würfe, bei denen eine 5 erzielt wird, und ist binomialverteilt mit $B_{500;0,6}$ -verteilt.

Es gilt:

$P(Z\geq 318) = 1-P(Z\leq 317) \approx 0,054$

Die Wahrscheinlichkeit für den Fehler zweiter Art beträgt somit ca. $5,4\,\%.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?