Wahlteil A1
Aufgabe A1.1
Der Graph der Funktion  mit
mit  beschreibt modellhaft für
beschreibt modellhaft für  das Profil eines Geländequerschnitts.
das Profil eines Geländequerschnitts.
Die positive -Achse weist nach Osten,
-Achse weist nach Osten,  gibt die Höhe über dem Meeresspiegel an (1 Längeneinheit entspricht 100 m).
gibt die Höhe über dem Meeresspiegel an (1 Längeneinheit entspricht 100 m).
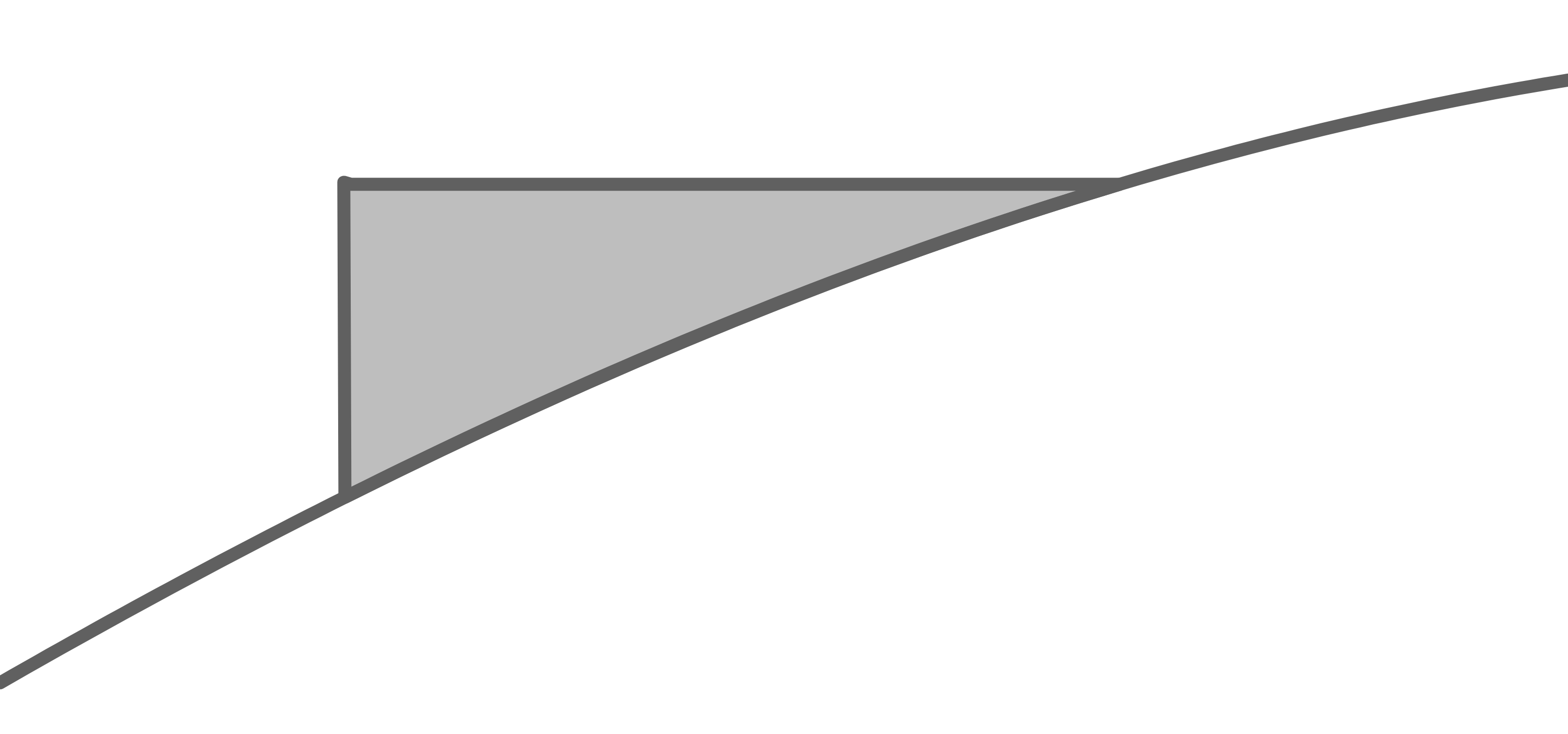 Die Abbildung zeigt den sichtbaren Teil dieser Seitenwand. Die Oberkante der Wand verläuft waagrecht auf
Die Abbildung zeigt den sichtbaren Teil dieser Seitenwand. Die Oberkante der Wand verläuft waagrecht auf  Höhe. Von dieser Kante sind
Höhe. Von dieser Kante sind  sichtbar.
sichtbar.
Untersuche, ob der Flächeninhalt des sichtbaren Wandteils größer als ist.
ist.
Die positive
a)
Auf welcher Höhe liegt der höchste Punkt des Profils?
In dem Tal westlich dieses Punktes befindet sich ein See, der im Geländequerschnitt an seiner tiefsten Stelle tief ist.
tief ist.
Bestimme die Breite des Sees im Geländequerschnitt.
Ab einer Hangneigung von besteht die Gefahr, dass sich Lawinen lösen.
besteht die Gefahr, dass sich Lawinen lösen.
Besteht an der steilsten Stelle des Profils zwischen See und höchstem Punkt Lawinengefahr?
In dem Tal westlich dieses Punktes befindet sich ein See, der im Geländequerschnitt an seiner tiefsten Stelle
Bestimme die Breite des Sees im Geländequerschnitt.
Ab einer Hangneigung von
Besteht an der steilsten Stelle des Profils zwischen See und höchstem Punkt Lawinengefahr?
(5 VP)
b)
Am Hang zwischen dem höchsten Punkt und dem westlich davon gelegenen Tal befindet sich ein in den Hang gebautes Gebäude, dessen rechteckige Seitenwand im Geländequerschnitt liegt.

Untersuche, ob der Flächeninhalt des sichtbaren Wandteils größer als
(3 VP)
c)
Der weitere Verlauf des Profils nach Osten hin kann durch eine Parabel zweiter Ordnung modelliert werden, die sich ohne Knick an den Graphen von  anschließt. Ihr Scheitel liegt bei
anschließt. Ihr Scheitel liegt bei  und beschreibt den tiefsten Punkt eines benachbarten Tals.
und beschreibt den tiefsten Punkt eines benachbarten Tals.
Auf welcher Höhe befindet sich dieser Punkt?
Auf welcher Höhe befindet sich dieser Punkt?
(4 VP)
Aufgabe A1.2
Gegeben ist die Funktion  mit
mit  deren Graph symmetrisch zur
deren Graph symmetrisch zur  -Achse ist. Es gibt einen Kreis, der den Graphen von
-Achse ist. Es gibt einen Kreis, der den Graphen von  in dessen Schnittpunkten mit der
in dessen Schnittpunkten mit der  -Achse berührt.
-Achse berührt.
Berechne die Koordinaten des Mittelpunkts dieses Kreises.
Berechne die Koordinaten des Mittelpunkts dieses Kreises.
(3 VP)
Aufgabe A 1.1
a)
1. Schritt: Hochpunkt bestimmen
Lass dir also den Graphen in deinem GTR anzeigen. Den Befehl für ein Maximum findest du dann unter:
 .
.
2ND  TRACE (CALC)
TRACE (CALC)  4: maximum
4: maximum
Der GTR liefert dir einen Hochpunkt mit den ungefähren Koordinaten  Abb. 1: Maximum bestimmen
Abb. 1: Maximum bestimmen
2ND  TRACE (CALC)
TRACE (CALC)  1: value
1: value
Du erhältst folgende Funktionswerte:
 Abb. 4: Skizze des Sees
Abb. 4: Skizze des Sees
Mit Hilfe der angegebenen Tiefe des Sees kannst du eine Gleichung für die Gerade
Du kannst nun erst die Koordinaten des Tiefpunkts mit Hilfe deines GTR bestimmen. Den Befehl dafür findest du unter:
 .
.
2ND  TRACE (CALC)
TRACE (CALC)  3: minimum
3: minimum
Du erhältst die Koordinaten  Abb. 5: Tiefpunkt
Abb. 5: Tiefpunkt
Also gilt:
2ND  TRACE (CALC)
TRACE (CALC)  5: intersect
5: intersect
Die Koordinaten lauten gerundet  Abb. 6: 1. Schnittpunkt
Abb. 6: 1. Schnittpunkt
 Abb. 7: 2. Schnittpunkt
Abb. 7: 2. Schnittpunkt
Mit dem GTR erhältst du, dass die Stelle mit dem steilsten Anstieg bei  liegt. Der Funktionswert von
liegt. Der Funktionswert von  an dieser Stelle beschreibt die Steigung, also beträgt sie ca.
an dieser Stelle beschreibt die Steigung, also beträgt sie ca.  . Den Steigungswinkel
. Den Steigungswinkel  kannst du mit Hilfe folgender Formel bestimmen.
kannst du mit Hilfe folgender Formel bestimmen.  ist dabei die Steigung des Graphen an der entsprechenden Stelle.
ist dabei die Steigung des Graphen an der entsprechenden Stelle.

![\(\begin{array}[t]{rll}
\tan(\alpha)&=& 0,83 &\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha&\approx& 39,69\,^{\circ} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0b6075c9ea40aa1f3d6606dc19c6cd74b8dc7b048a2ba330ddece1174fe795b4?color=5a5a5a)
 Abb. 8: Maximale Steigung
Abb. 8: Maximale Steigung
b)
 Abb. 9: Skizze zur Hauswand
Abb. 9: Skizze zur Hauswand
Du kannst die Koordinaten von  wie oben mit deinem GTR berechnen. Beachte, dass es mehr als einen Schnittpunkt geben kann, das Gebäude aber westlich des höchsten Punkts liegt.
Der GTR liefert dir den Schnittpunkt
wie oben mit deinem GTR berechnen. Beachte, dass es mehr als einen Schnittpunkt geben kann, das Gebäude aber westlich des höchsten Punkts liegt.
Der GTR liefert dir den Schnittpunkt  . Die obere Grenze des Integrals ist demnach
. Die obere Grenze des Integrals ist demnach  . Die obere Kante ist
. Die obere Kante ist  lang, also beträgt der Abstand zwischen
lang, also beträgt der Abstand zwischen  und
und 
 Längeneinheiten. Die
Längeneinheiten. Die  -Koordinate von
-Koordinate von  ist also
ist also  .
.
 Abb. 10: Schnittpunkt
Abb. 10: Schnittpunkt
Dies kannst du ebenfalls mit deinem GTR berechnen. Lass dir dazu den Graphen zur Funktion  anzeigen. Den Befehl für ein Integral findest du dann unter:
anzeigen. Den Befehl für ein Integral findest du dann unter:

2ND  TRACE (CALC)
TRACE (CALC)  7:
7: 
Du erhältst folgendes Ergebnis:
 Abb. 11: Integral
Abb. 11: Integral
c)
- Nahtloser Übergang vom Graphen von
zur Parabel:
- Gleicher Funktionswert an der Übergangsstelle
- Gleiche Steigung bei
- Gleicher Funktionswert an der Übergangsstelle
- Scheitelpunkt/Tiefpunkt an der Stelle
Die Koordinaten des Tiefpunkts der Parabel kannst du nun entweder über die minimum-Funktion oder die value-Funktion deines GTR bestimmen, indem du den Funktionswert an der Stelle  bestimmst, da du bereits weißt, dass dort der Tiefpunkt liegen soll:
bestimmst, da du bereits weißt, dass dort der Tiefpunkt liegen soll:
 Um die Höhe des Punktes im Gelände zu berechnen, beachte wieder den Maßstab:
Um die Höhe des Punktes im Gelände zu berechnen, beachte wieder den Maßstab:

 Abb. 12: Funktionswert bestimmen
Abb. 12: Funktionswert bestimmen
Aufgabe A 1.2
 Abb. 13: Schaubild des Graphen
Abb. 13: Schaubild des Graphen
Der Kreis soll den Graphen in den Schnittpunkten mit der  -Achse nur berühren, ihn aber nicht schneiden. Die jeweilige Tangente an den Graphen in diesen Punkten, soll also auch eine Tangente an den Kreis sein. Das bedeutet, dass die Tangente senkrecht liegen muss, zu der Strecke, die den betrachteten Punkt mit dem Mittelpunkt verbindet.
Der Mittelpunkt
-Achse nur berühren, ihn aber nicht schneiden. Die jeweilige Tangente an den Graphen in diesen Punkten, soll also auch eine Tangente an den Kreis sein. Das bedeutet, dass die Tangente senkrecht liegen muss, zu der Strecke, die den betrachteten Punkt mit dem Mittelpunkt verbindet.
Der Mittelpunkt  muss also auf der Normalen von
muss also auf der Normalen von  in diesem Punkt liegen, dies gilt für beide Schnittpunkte mit der
in diesem Punkt liegen, dies gilt für beide Schnittpunkte mit der  -Achse. Da der Graph achsensymmetrisch zur
-Achse. Da der Graph achsensymmetrisch zur  -Achse ist, ist
-Achse ist, ist  genau der Schnittpunkt beider Normalen mit der
genau der Schnittpunkt beider Normalen mit der  -Achse und es genügt die Normale nur für einen der beiden Schnittpunkte zu bestimmen.
-Achse und es genügt die Normale nur für einen der beiden Schnittpunkte zu bestimmen.
 Abb. 14: Kreisskizze
Abb. 14: Kreisskizze
Die Schnittpunkte mit der  -Achse kannst du mit deinem GTR über folgenden Befehl bestimmen:
-Achse kannst du mit deinem GTR über folgenden Befehl bestimmen:
 und
und 
2ND  TRACE (CALC)
TRACE (CALC)  2: zero
2: zero
Dann erhältst du folgende Schnittpunkte:
 Abb. 15: Schaubild des Graphen
Abb. 15: Schaubild des Graphen
Betrachtest du den Schnittpunkt  , kannst du die Steigung
, kannst du die Steigung  mit deinem GTR über folgenden Befehl berechnen:
mit deinem GTR über folgenden Befehl berechnen:
 und damit für die Steigung der Normalen:
und damit für die Steigung der Normalen:

2ND  TRACE (CALC)
TRACE (CALC)  6:
6: 
Du erhältst dann:  Abb. 16: Steigungsberechnung
Abb. 16: Steigungsberechnung
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabe A 1.1
a)
Lass dir also den Graphen in deinem GTR anzeigen. Den Befehl für ein Maximum findest du dann unter:
 .
.
F5 (G-Solv)  F2 (MAX)
F2 (MAX)
Der GTR liefert dir einen Hochpunkt mit den ungefähren Koordinaten  Abb. 1: Maximum bestimmen
Abb. 1: Maximum bestimmen
2ND  TRACE (CALC)
TRACE (CALC)  1: value
1: value
Du erhältst folgende Funktionswerte:
 Abb. 4: Skizze des Sees
Abb. 4: Skizze des Sees
Mit Hilfe der angegebenen Tiefe des Sees kannst du eine Gleichung für die Gerade
Du kannst nun erst die Koordinaten des Tiefpunkts mit Hilfe deines GTR bestimmen. Den Befehl dafür findest du unter:
 .
.
F5(G-Solv)  F3(MIN)
F3(MIN)
Du erhältst die Koordinaten  Abb. 5: Tiefpunkt
Abb. 5: Tiefpunkt
Also gilt:
F5(G-Solv)  F5 (ISCT)
F5 (ISCT)
Die Koordinaten lauten gerundet  Abb. 6: 1. Schnittpunkt
Abb. 6: 1. Schnittpunkt
 Abb. 7: 2. Schnittpunkt
Abb. 7: 2. Schnittpunkt
Mit dem GTR erhältst du, dass die Stelle mit dem steilsten Anstieg bei  liegt. Der Funktionswert von
liegt. Der Funktionswert von  an dieser Stelle beschreibt die Steigung, also beträgt sie ca.
an dieser Stelle beschreibt die Steigung, also beträgt sie ca.  . Den Steigungswinkel
. Den Steigungswinkel  kannst du mit Hilfe folgender Formel bestimmen.
kannst du mit Hilfe folgender Formel bestimmen.  ist dabei die Steigung des Graphen an der entsprechenden Stelle.
ist dabei die Steigung des Graphen an der entsprechenden Stelle.

![\(\begin{array}[t]{rll}
\tan(\alpha)&=& 0,83 &\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha&\approx& 39,69\,^{\circ} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0b6075c9ea40aa1f3d6606dc19c6cd74b8dc7b048a2ba330ddece1174fe795b4?color=5a5a5a)
 Abb. 8: Maximale Steigung
Abb. 8: Maximale Steigung
b)
 Abb. 9: Skizze zur Hauswand
Abb. 9: Skizze zur Hauswand
Du kannst die Koordinaten von  wie oben mit deinem GTR berechnen. Beachte, dass es mehr als einen Schnittpunkt geben kann, das Gebäude aber westlich des höchsten Punkts liegt.
Der GTR liefert dir den Schnittpunkt
wie oben mit deinem GTR berechnen. Beachte, dass es mehr als einen Schnittpunkt geben kann, das Gebäude aber westlich des höchsten Punkts liegt.
Der GTR liefert dir den Schnittpunkt  . Die obere Grenze des Integrals ist demnach
. Die obere Grenze des Integrals ist demnach  . Die obere Kante ist
. Die obere Kante ist  lang, also beträgt der Abstand zwischen
lang, also beträgt der Abstand zwischen  und
und 
 Längeneinheiten. Die
Längeneinheiten. Die  -Koordinate von
-Koordinate von  ist also
ist also  .
.
 Abb. 10: Schnittpunkt
Abb. 10: Schnittpunkt
Dies kannst du ebenfalls mit deinem GTR berechnen. Lass dir dazu den Graphen zur Funktion  anzeigen. Den Befehl für ein Integral findest du dann unter:
anzeigen. Den Befehl für ein Integral findest du dann unter:

F5 (G-Solv)  F6 (
F6 ( )
)  F3
F3 
Du erhältst folgendes Ergebnis:
 Abb. 11: Integral
Abb. 11: Integral
c)
- Nahtloser Übergang vom Graphen von
zur Parabel:
- Gleicher Funktionswert an der Übergangsstelle
- Gleiche Steigung bei
- Gleicher Funktionswert an der Übergangsstelle
- Scheitelpunkt/Tiefpunkt an der Stelle
Die Koordinaten des Tiefpunkts der Parabel kannst du nun entweder über die minimum-Funktion oder die value-Funktion deines GTR bestimmen, indem du den Funktionswert an der Stelle  bestimmst, da du bereits weißt, dass dort der Tiefpunkt liegen soll:
bestimmst, da du bereits weißt, dass dort der Tiefpunkt liegen soll:
 Um die Höhe des Punktes im Gelände zu berechnen, beachte wieder den Maßstab:
Um die Höhe des Punktes im Gelände zu berechnen, beachte wieder den Maßstab:

 Abb. 12: Funktionswert bestimmen
Abb. 12: Funktionswert bestimmen
Aufgabe A 1.2
 Abb. 13: Schubild des Graphen
Abb. 13: Schubild des Graphen
Der Kreis soll den Graphen in den Schnittpunkten mit der  -Achse nur berühren, ihn aber nicht schneiden. Die jeweilige Tangente an den Graphen in diesen Punkten, soll also auch eine Tangente an den Kreis sein. Das bedeutet, dass die Tangente senkrecht liegen muss, zu der Strecke, die den betrachteten Punkt mit dem Mittelpunkt verbindet.
Der Mittelpunkt
-Achse nur berühren, ihn aber nicht schneiden. Die jeweilige Tangente an den Graphen in diesen Punkten, soll also auch eine Tangente an den Kreis sein. Das bedeutet, dass die Tangente senkrecht liegen muss, zu der Strecke, die den betrachteten Punkt mit dem Mittelpunkt verbindet.
Der Mittelpunkt  muss also auf der Normalen von
muss also auf der Normalen von  in diesem Punkt liegen, dies gilt für beide Schnittpunkte mit der
in diesem Punkt liegen, dies gilt für beide Schnittpunkte mit der  -Achse. Da der Graph achsensymmetrisch zur
-Achse. Da der Graph achsensymmetrisch zur  -Achse ist, ist
-Achse ist, ist  genau der Schnittpunkt beider Normalen mit der
genau der Schnittpunkt beider Normalen mit der  -Achse und es genügt die Normale nur für einen der beiden Schnittpunkte zu bestimmen.
-Achse und es genügt die Normale nur für einen der beiden Schnittpunkte zu bestimmen.
 Abb. 14: Kreisskizze
Abb. 14: Kreisskizze
Die Schnittpunkte mit der  -Achse kannst du mit deinem GTR über folgenden Befehl bestimmen:
-Achse kannst du mit deinem GTR über folgenden Befehl bestimmen:
 und
und 
F5 (G-Solv)  F1 (ROOT)
F1 (ROOT)
Dann erhältst du folgende Schnittpunkte:
 Abb. 15: Schubild des Graphen
Abb. 15: Schubild des Graphen
Du erhältst dann:  und damit für die Steigung der Normalen:
und damit für die Steigung der Normalen:
 Damit die Normale ebenfalls durch den Punkt
Damit die Normale ebenfalls durch den Punkt  läuft, musst du nun noch die Koordinaten in die Funktionsgleichung einsetzen, um
läuft, musst du nun noch die Koordinaten in die Funktionsgleichung einsetzen, um  zu berechnen:
zu berechnen:
 Abb. 16: Steigungsberechnung
Abb. 16: Steigungsberechnung
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.



