Wahlteil A2
Aufgabe A2.1
Die Entwicklung einer Population in den Jahren 1960 bis 2020 lässt sich durch zwei Funktionen modellhaft beschreiben.
Die Funktion mit
mit  beschreibt die Geburtenrate und die Funktion
beschreibt die Geburtenrate und die Funktion  mit
mit 
 beschreibt die Sterberate der Population
beschreibt die Sterberate der Population  in Jahren seit Beginn des Jahres 1960,
in Jahren seit Beginn des Jahres 1960,  und
und  in Individuen pro Jahr).
in Individuen pro Jahr).
Die Funktion
a)
Bestimme die geringste Sterberate.
In welchem Jahr war die Differenz aus Geburten- und Sterberate am größten?
Bestimme den Zeitraum, in dem die Population zugenommen hat.
In welchem Jahr war die Differenz aus Geburten- und Sterberate am größten?
Bestimme den Zeitraum, in dem die Population zugenommen hat.
(4 VP)
b)
Zu Beginn des Jahres 1960 bestand die Population aus 20.000 Individuen.
Berechne den Bestand der Population zu Beginn des Jahres 2017.
In welchem Jahr erreichte die Population erstmals wieder den Bestand von 1960?
Berechne den Bestand der Population zu Beginn des Jahres 2017.
In welchem Jahr erreichte die Population erstmals wieder den Bestand von 1960?
(3 VP)
Betrachtet wird nun das Größenwachstum eines einzelnen Individuums der Population. Dies kann im Beobachtungszeitraumdurch das Gesetz des beschränkten Wachstums modelliert werden. Man geht davon aus, dass dieses Individuum in ausgewachsenem Zustand  groß ist. Zu Beobachtungsbeginn betragen seine Größe
groß ist. Zu Beobachtungsbeginn betragen seine Größe  und seine momentane Wachstumsgeschwindigkeit
und seine momentane Wachstumsgeschwindigkeit  pro Jahr.
pro Jahr.
c)
Bestimme eine Gleichung einer Funktion, die die Körpergröße des Individuums in Abhängigkeit von der Zeit beschreibt.
Wie viele Jahre nach Beobachtungsbeginn hat die Körpergröße des Individuums um 50% zugenommen?
Wie viele Jahre nach Beobachtungsbeginn hat die Körpergröße des Individuums um 50% zugenommen?
(4 VP)
Aufgabe A2.2
Gegeben sind ein Kreis mit Mittelpunkt  und die Funktion
und die Funktion  mit
mit  .
Bestimme die Anzahl der gemeinsamen Punkte des Kreises mit dem Graphen von
.
Bestimme die Anzahl der gemeinsamen Punkte des Kreises mit dem Graphen von  in Abhängigkeit vom Kreisradius.
in Abhängigkeit vom Kreisradius.
(4 VP)
Aufgabe 2.1
a)
Da
2nd  CALC
CALC  3: minimum
3: minimum
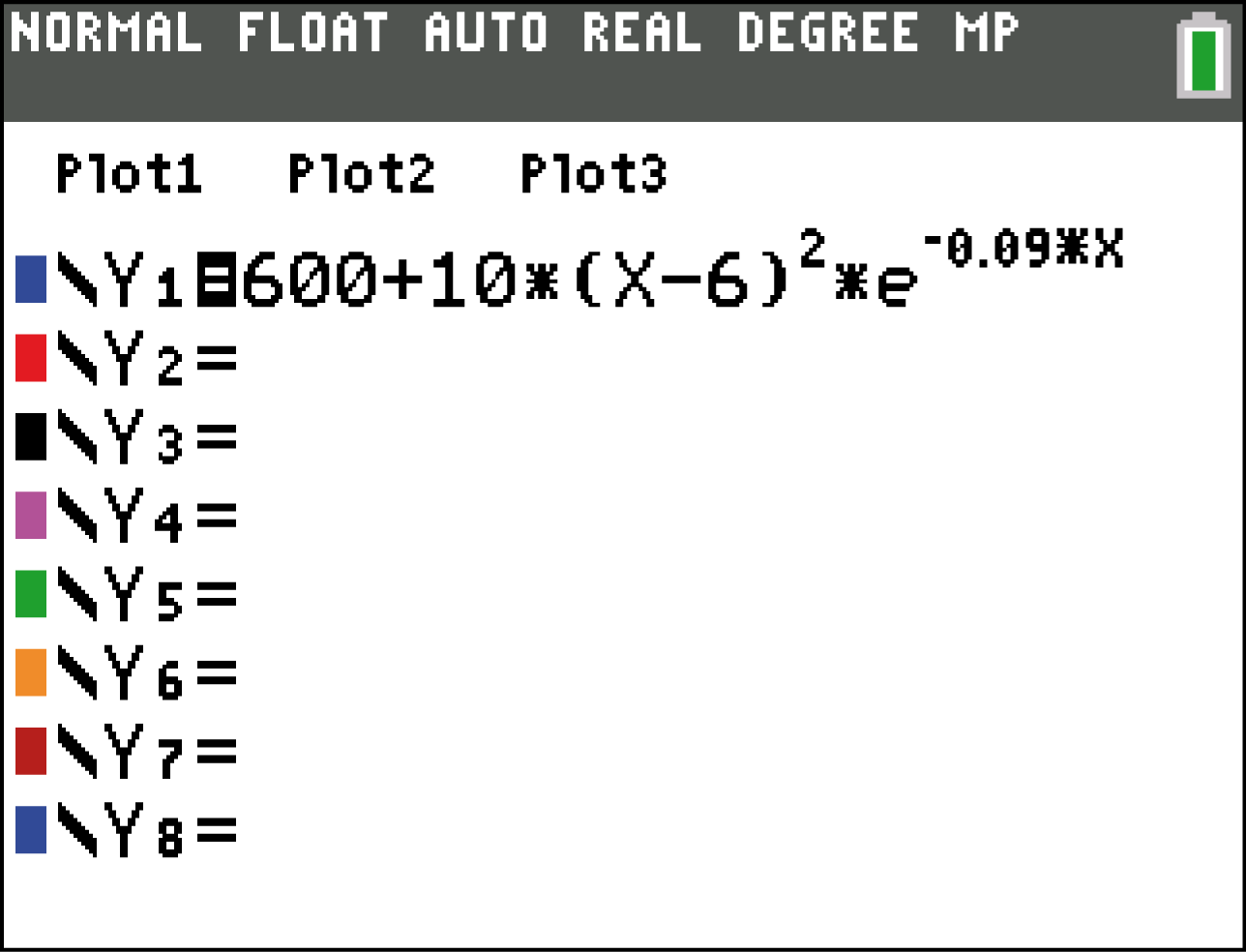
Bilde dazu eine Differenzfunktion und bestimme mit deinem GTR die Maximalstelle dieser Funktion. Da die gegenseitge Lage der Graphen von
2nd  CALC
CALC  4: maximum
4: maximum
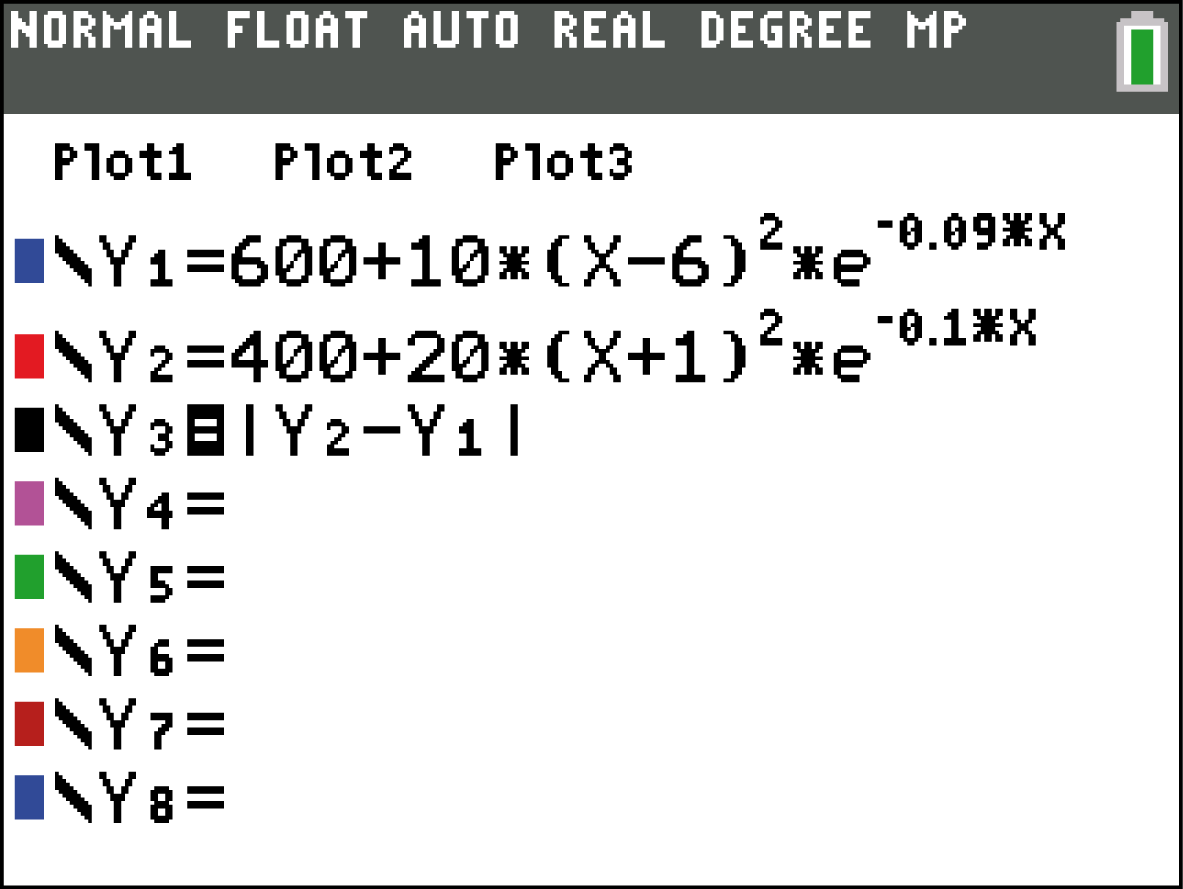
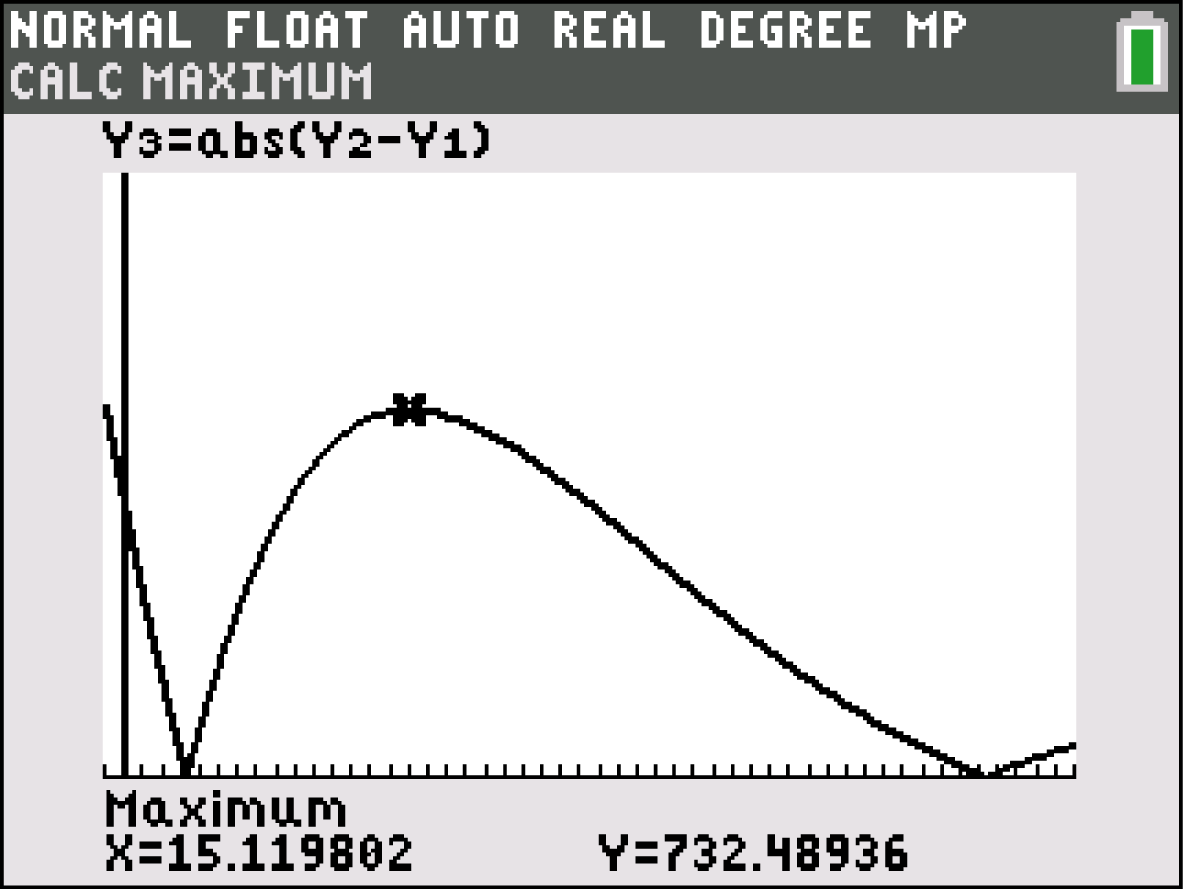
Es ergibt sich:  .
.
Im Jahr 1975 war die Differenz zwischen Geburten- und Sterberate am größten. Bestimmen des Zeitraums in dem die Population zugenommen hat
Die Population nimmt dann zu, wenn die Differenz zwischen Geburten und Sterberate positiv ist. Definiere also eine Funktion
Bestimmen des Zeitraums in dem die Population zugenommen hat
Die Population nimmt dann zu, wenn die Differenz zwischen Geburten und Sterberate positiv ist. Definiere also eine Funktion  , die diesen Sachverhalt beschreibt:
, die diesen Sachverhalt beschreibt:
 Der Zeitraum indem die Population zugenommen hat kannst du bestimmen, indem du den Bereich bestimmst, indem der Graph von
Der Zeitraum indem die Population zugenommen hat kannst du bestimmen, indem du den Bereich bestimmst, indem der Graph von  oberhalb der
oberhalb der  -Achse verläuft. Betrachte dazu den Graphen von
-Achse verläuft. Betrachte dazu den Graphen von  im GTR und bestimme die Nullstellen.
Übertrage den Funktionsterm wie oben in deinen GTR und berechne den gesuchten Zeitraum wie folgt:
im GTR und bestimme die Nullstellen.
Übertrage den Funktionsterm wie oben in deinen GTR und berechne den gesuchten Zeitraum wie folgt:
Im Jahr 1975 war die Differenz zwischen Geburten- und Sterberate am größten.
2nd  CALC
CALC  2: zero
2: zero
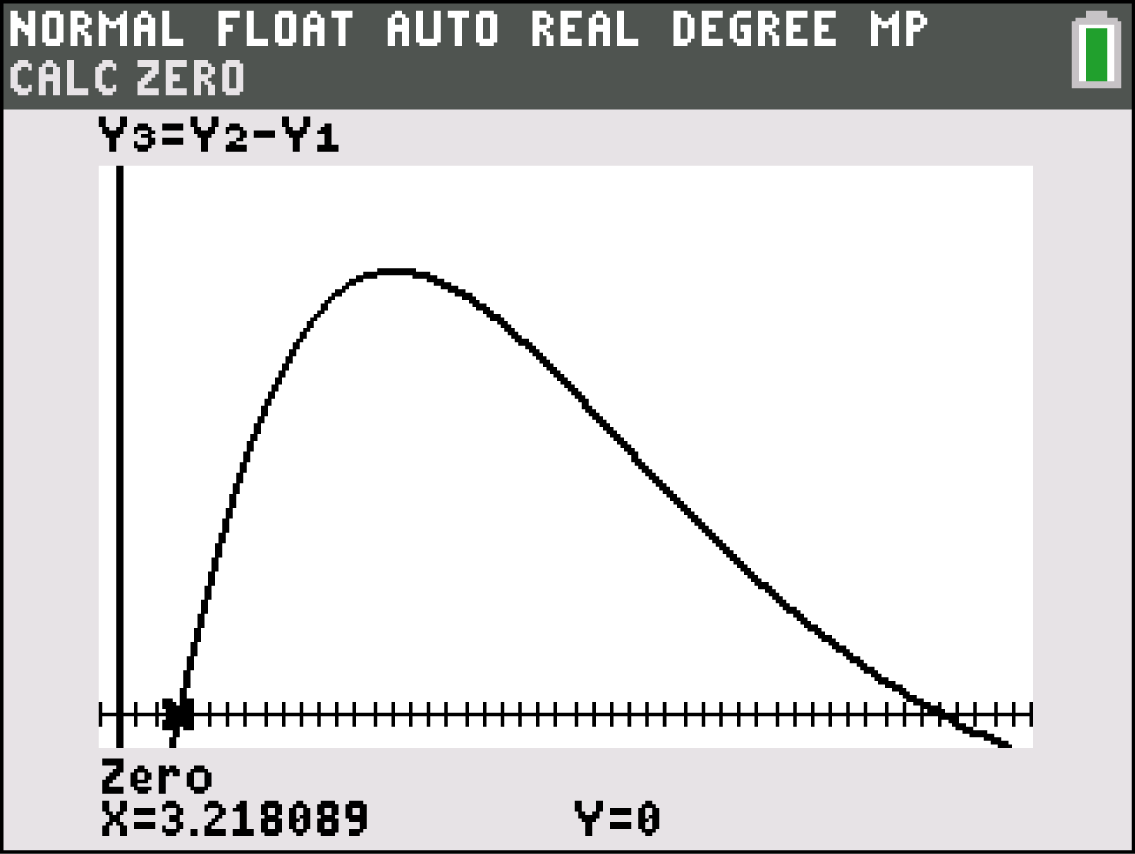
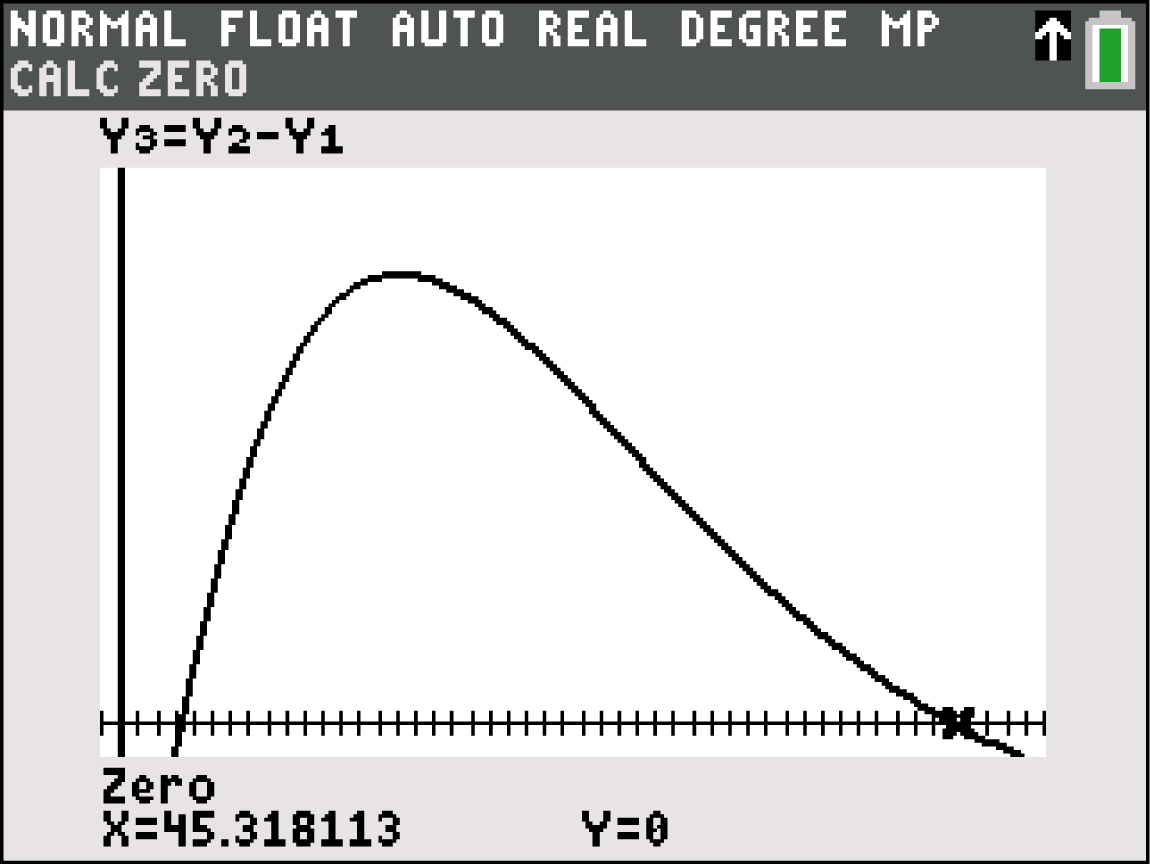
Die Bevölkerung hat im Zeitraum zwischen 1963 und 2005 zugenommen.
b)
Beachte hier, dass die Anzahl an Individuen wie oben durch die Differenz zwischen Geburten- und Sterberate definiert wird. Integriere also über
Verwende beim Berechnen deinen GTR. Integriere über
2nd  CALC
CALC 
 f(x)dx
f(x)dx
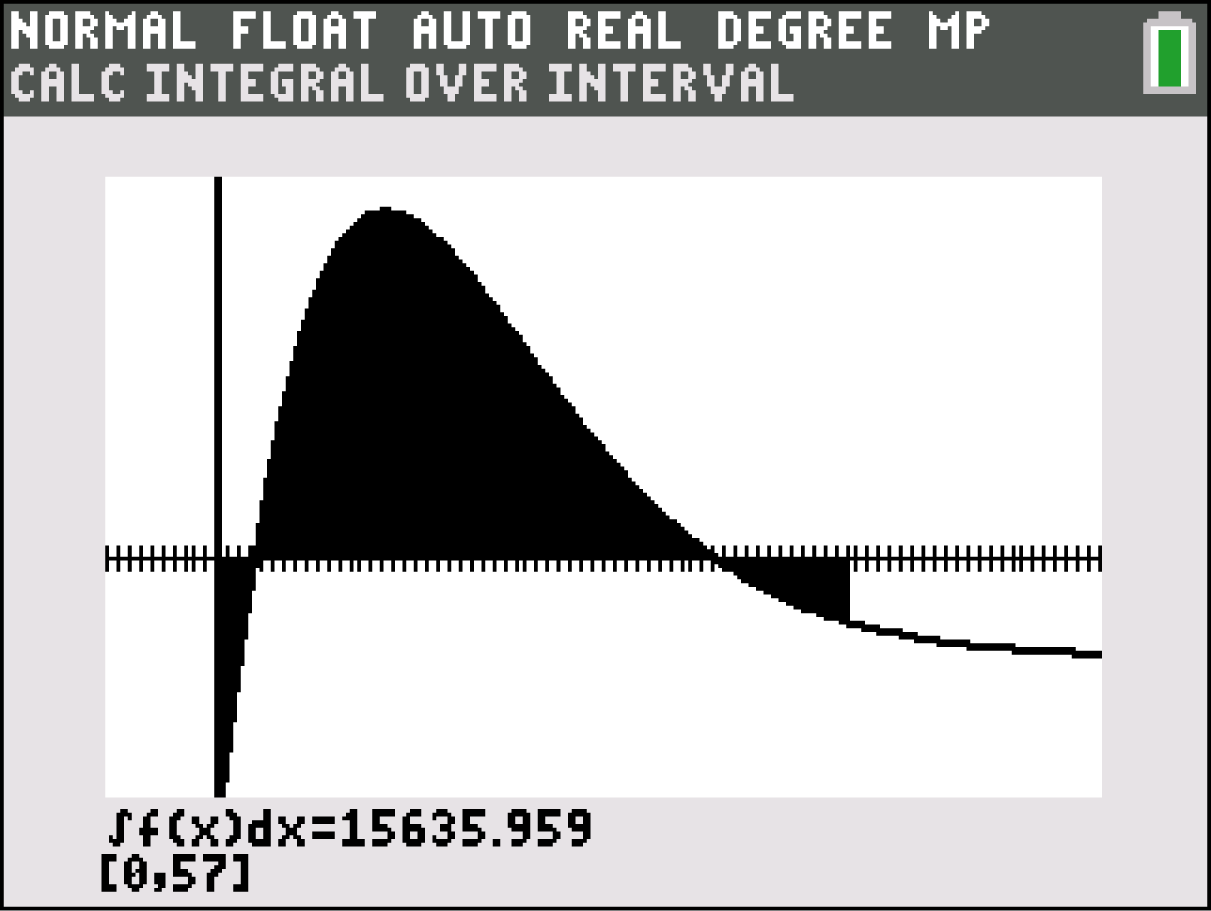
Population 2017
Oben haben wir mit dem Anfangsbestand und einem Integral über
Für das Integral bedeutet dies, dass die obere Integrationsgrenze unbekannt ist:
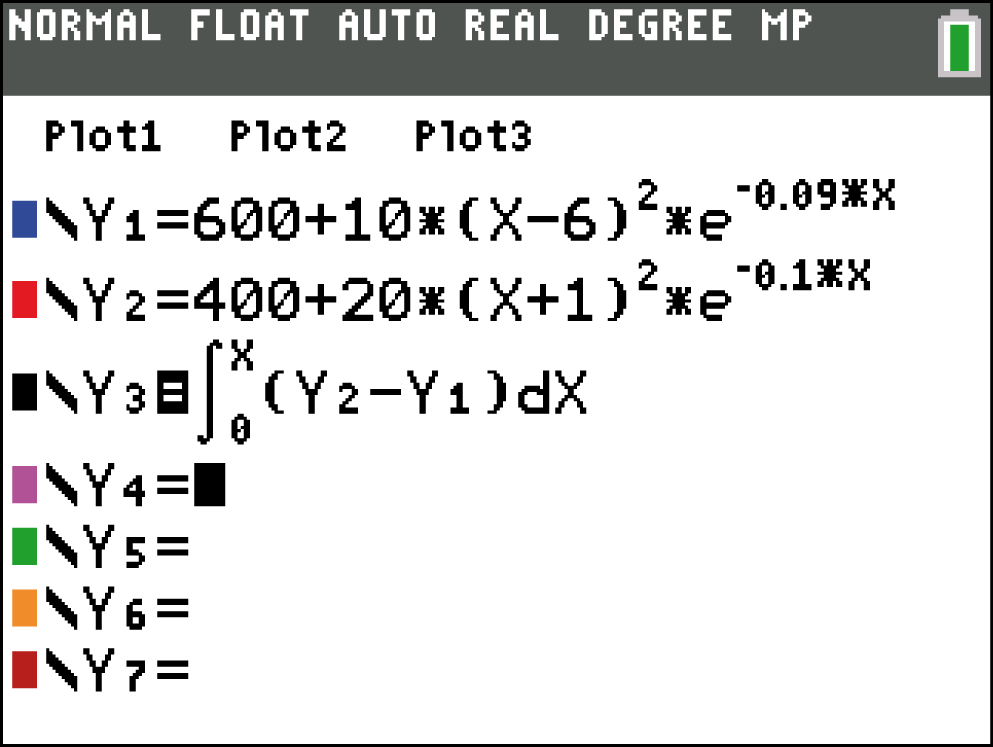
2nd  CALC
CALC  2: zero
2: zero
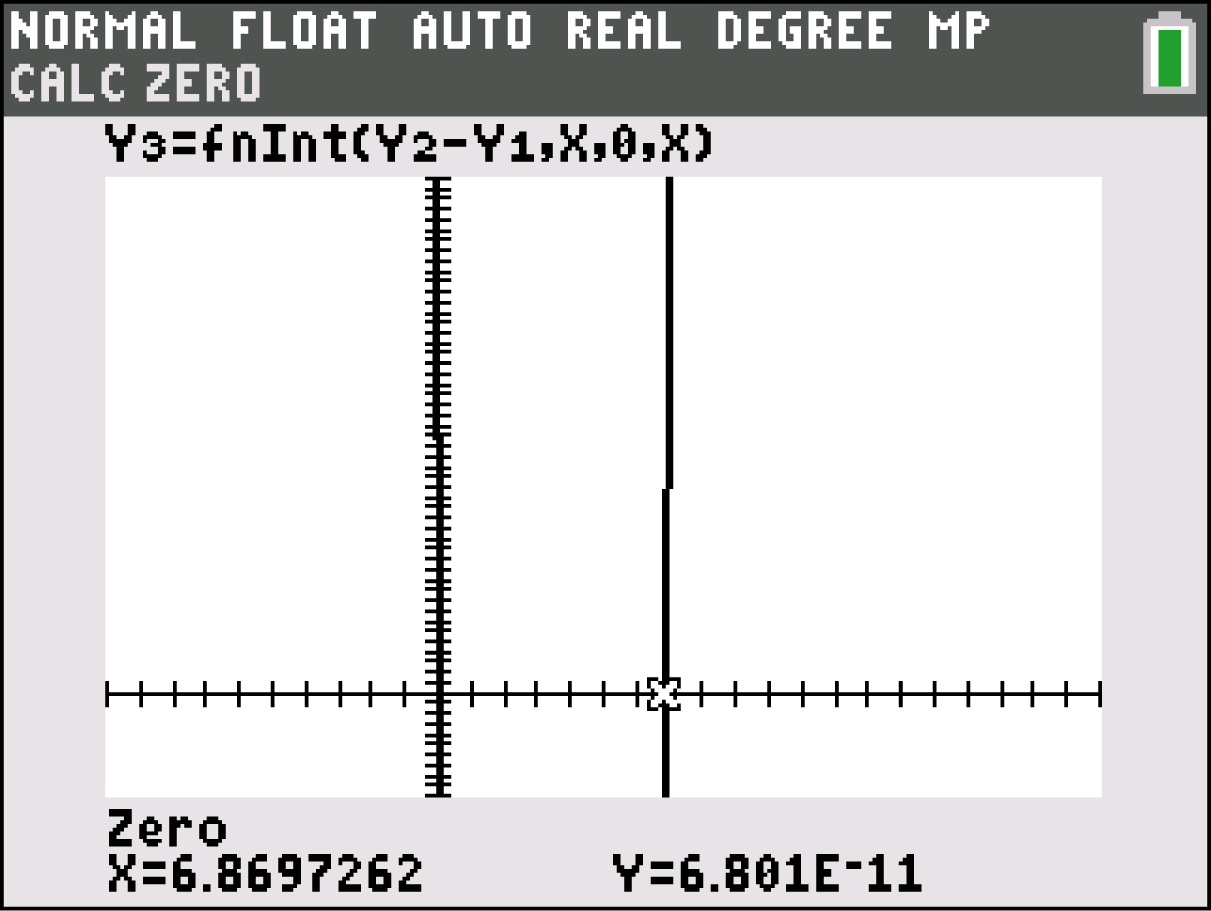
Daraus folgt, dass die Population erstmals im Jahr 1966 wieder einen Bestand von 20.000 erreichte.
c)
Folgende Angaben kannst du dazu der Aufgabenstellung entnehmen:
- Es liegt ein beschränktes Wachstum vor
- Ausgewachsen ist das Individuum 0,8
m groß
- Zum Zeitpunkt
ist das Individuum 0,5
m groß
- Seine Wachstumsgeschwindigkeit beträgt 0,15
m pro Jahr
Mit der Anfangsgröße
Du musst folglich den Zeitpunkt
Aufgabe 2.2
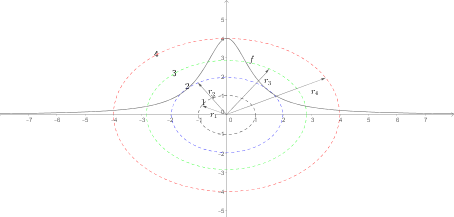
- Der Kreis und der Graph von
haben keinen Schnittpunkt (siehe
)
- Der Kreis und der Graph von
haben zwei Schnittpunkte (siehe
)
- Der Kreis und der Graph von
haben drei Schnittpunkte (siehe
)
- Der Kreis und der Graph von
haben vier Schnittpunkte (siehe
)
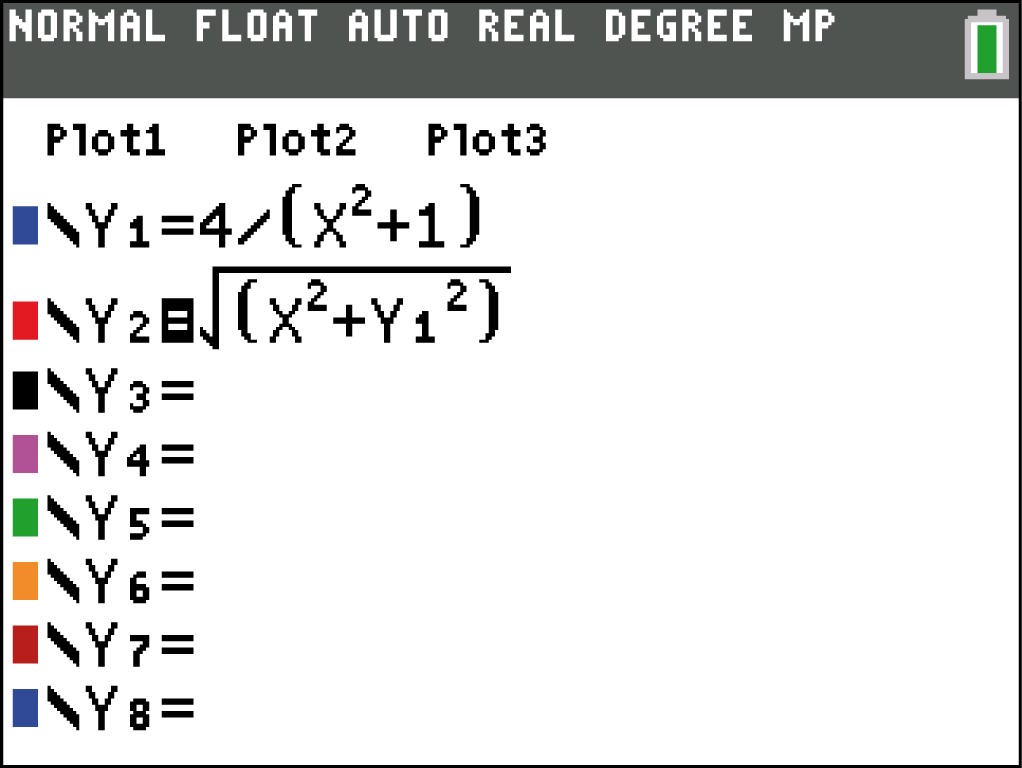
Definiere den Abstand
2nd  CALC
CALC  3: minimum
3: minimum
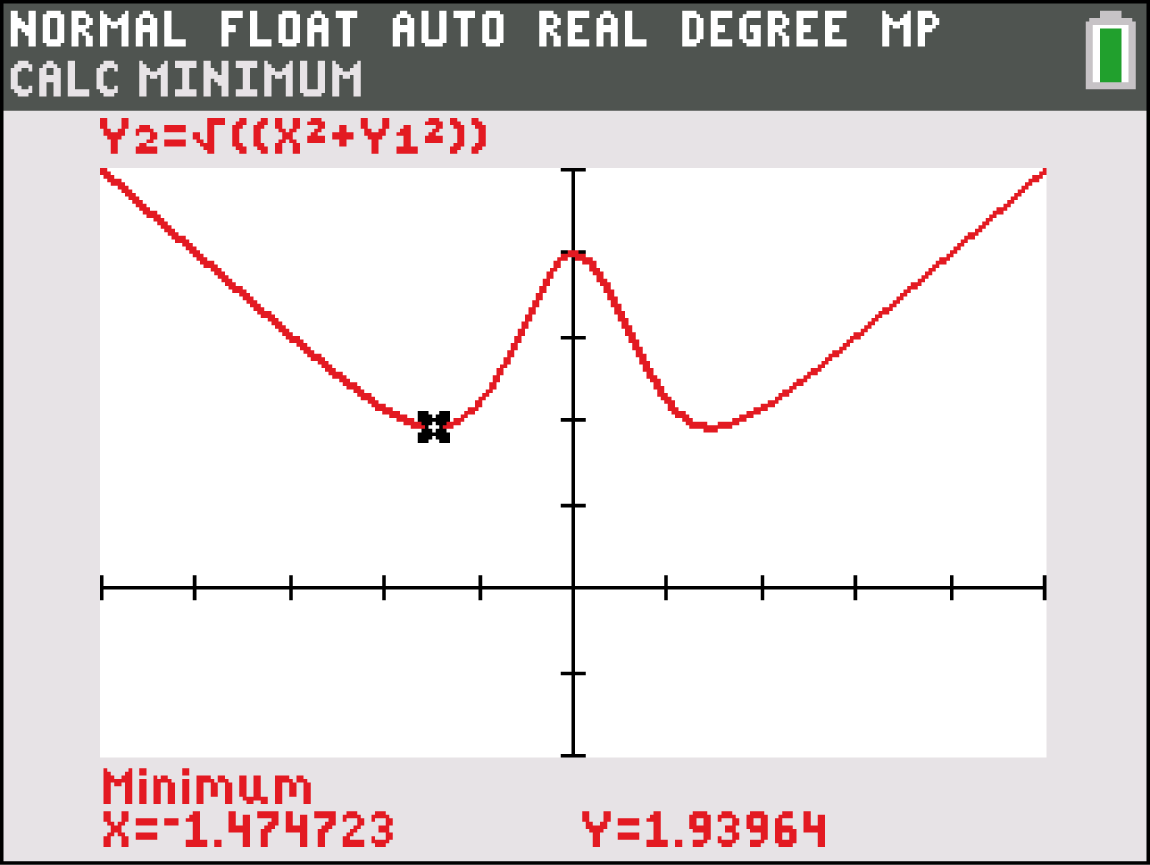
Der Skizze oben kannst du entnehmen, dass der Kreis auch für Radien, die größer sind als der Abstand zwischen
Für den Radius muss in diesem Fall gelten:
Hier gilt dann:
| Anz. Schnittpunkte | Radius |
|---|---|
| 0 | |
| 2 | |
| 3 | |
| 4 |
Aufgabe 2.1
a)
Da
SHIFT  G-Solv
G-Solv  MIN
MIN
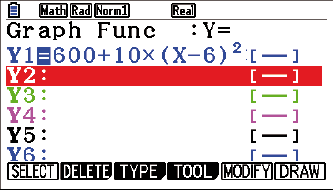
Bilde dazu eine Differenzfunktion und bestimme mit deinem GTR die Maximalstelle dieser Funktion. Da die gegenseitge Lage der Graphen von
SHIFT  G-Solv
G-Solv  MAX
MAX
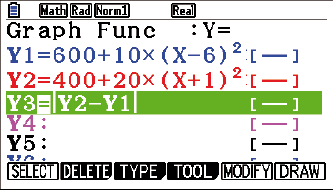
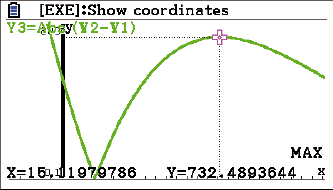
Im Jahr 1975 war die Differenz zwischen Geburten- und Sterberate am größten.
SHIFT  G-Solv
G-Solv  ROOT
ROOT
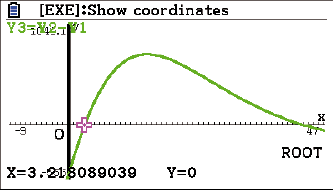
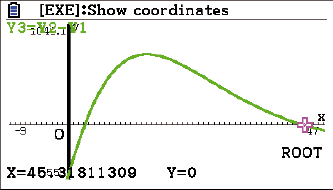
Die Bevölkerung hat im Zeitraum zwischen 1963 und 2005 zugenommen.
b)
Beachte hier, dass die Anzahl an Individuen wie oben durch die Differenz zwischen Geburten- und Sterberate definiert wird. Integriere also über
Verwende beim Berechnen deinen GTR. Integriere über
SHIFT  G-Solv
G-Solv 
 dx
dx
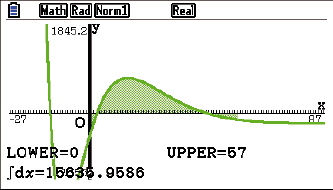
Population 2017
Oben haben wir mit dem Anfangsbestand und einem Integral über
Für das Integral bedeutet dies, dass die obere Integrationsgrenze unbekannt ist:

SHIFT  G-Solv
G-Solv  ROOT
ROOT

Daraus folgt, dass die Population erstmals im Jahr 1966 wieder einen Bestand von 20.000 erreichte.
c)
Folgende Angaben kannst du dazu der Aufgabenstellung entnehmen:
- Es liegt ein beschränktes Wachstum vor
- Ausgewachsen ist das Individuum 0,8
m groß
- Zum Zeitpunkt
ist das Individuum 0,5
m groß
- Seine Wachstumsgeschwindigkeit beträgt 0,15
m pro Jahr
Mit der Anfangsgröße
Du musst folglich den Zeitpunkt
Aufgabe 2.2

- Der Kreis und der Graph von
haben keinen Schnittpunkt (siehe
)
- Der Kreis und der Graph von
haben zwei Schnittpunkte (siehe
)
- Der Kreis und der Graph von
haben drei Schnittpunkte (siehe
)
- Der Kreis und der Graph von
haben vier Schnittpunkte (siehe
)
Definiere den Abstand
SHIFT  G-Solv
G-Solv  MIN
MIN
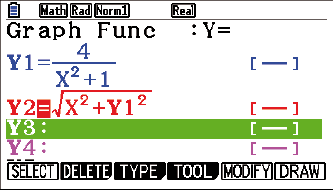
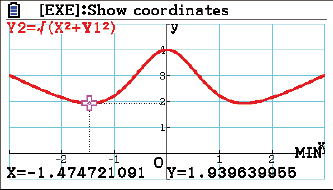
Der Skizze oben kannst du entnehmen, dass der Kreis auch für Radien, die größer sind als der Abstand zwischen
Für den Radius muss in diesem Fall gelten:
Hier gilt dann:
| Anz. Schnittpunkte | Radius |
|---|---|
| 0 | |
| 2 | |
| 3 | |
| 4 |