Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=x^4\cdot \sin (3x)$ .

(2 VP)

Aufgabe 2

Löse die Gleichung $(\cos (x))^2 +2\cos (x)=0$ für $0\leq x\leq 2\pi$ .

(2 VP)

Aufgabe 3

Gegeben ist die Funktion $f$ mit $f(x)=1-\dfrac{1}{x^2},$ die die Nullstellen $x_1= -1$ und $x_2 = 1$ hat. Die Abbildung zeigt den Graphen von $f,$ der symmetrisch zur $y$ -Achse ist. Weiterhin ist die Gerade $g$ mit der Gleichung $y=-3$ gegeben.

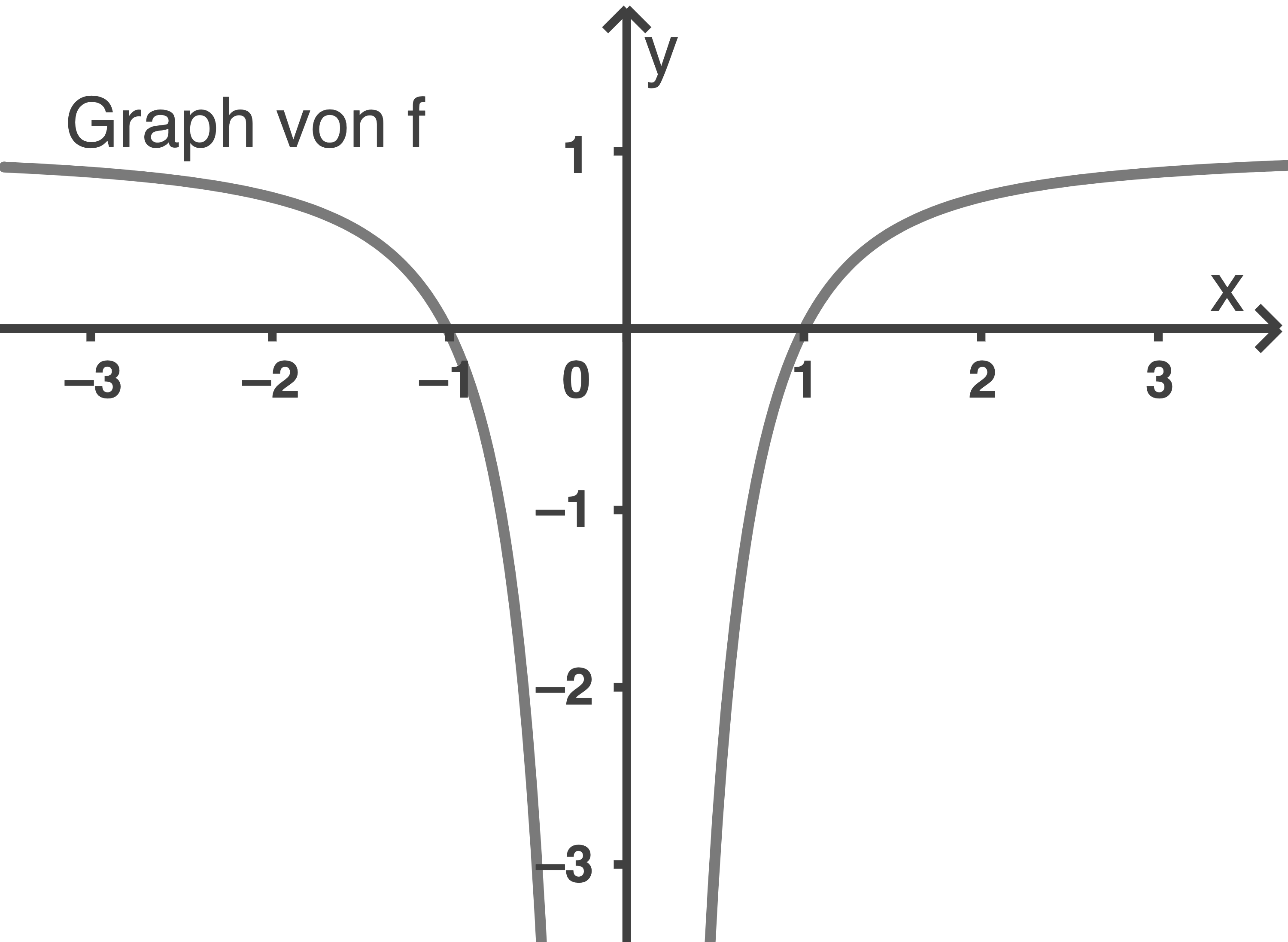
Graph einer Funktion in einem Koordinatensystem mit x- und y-Achse.

Zeige, dass einer der Punkte, in denen $g$ den Graphen von $f$ schneidet, die $x$ -Koordinate $\frac{1}{2}$ hat.

Bestimme rechnerisch den Inhalt der Fläche, die der Graph von $f,$ die $x$ -Achse und die Gerade $g$ einschließen.

(2,5 VP)

Aufgabe 4

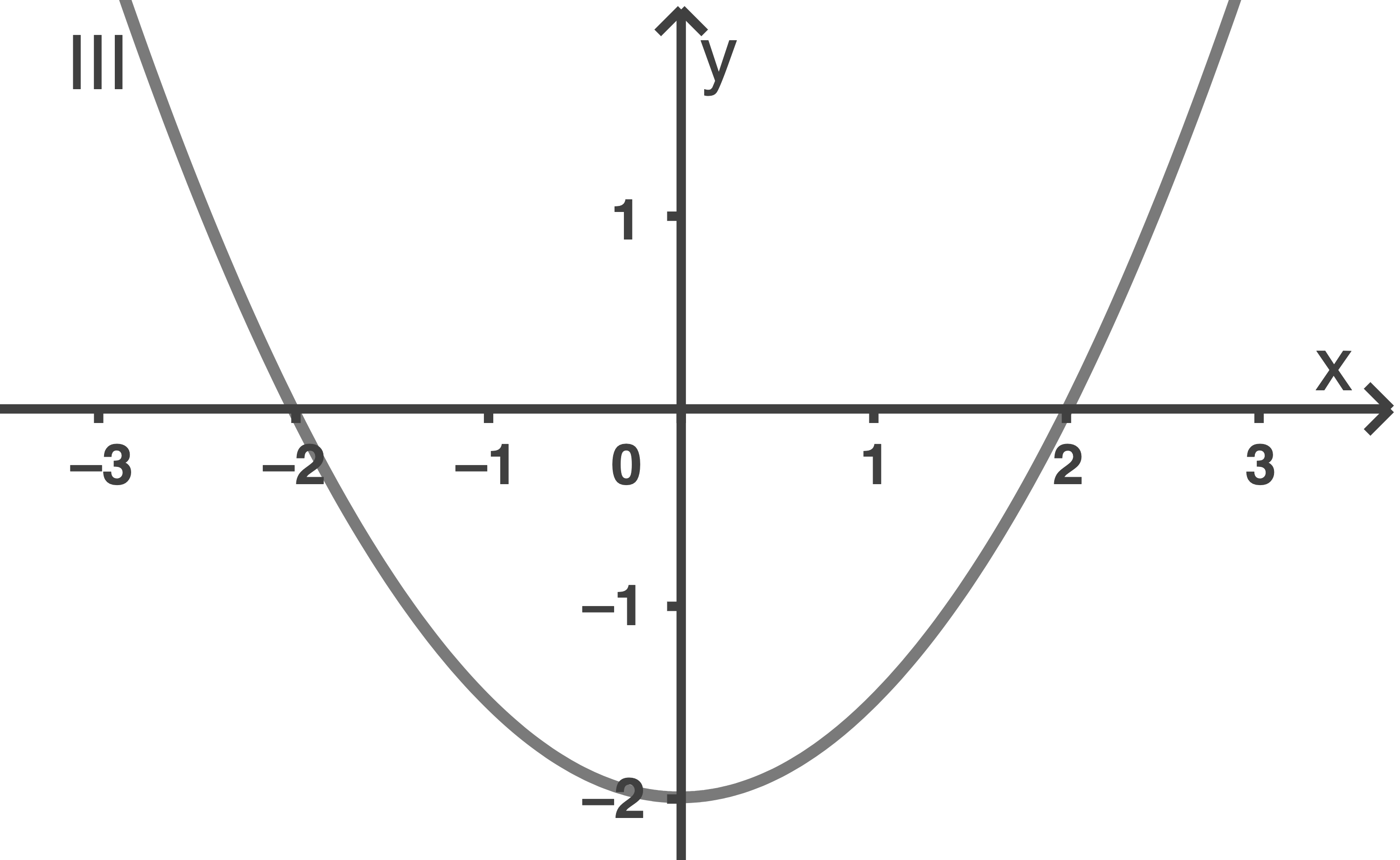
Die Abbildung zeigt den Graphen einer Funktion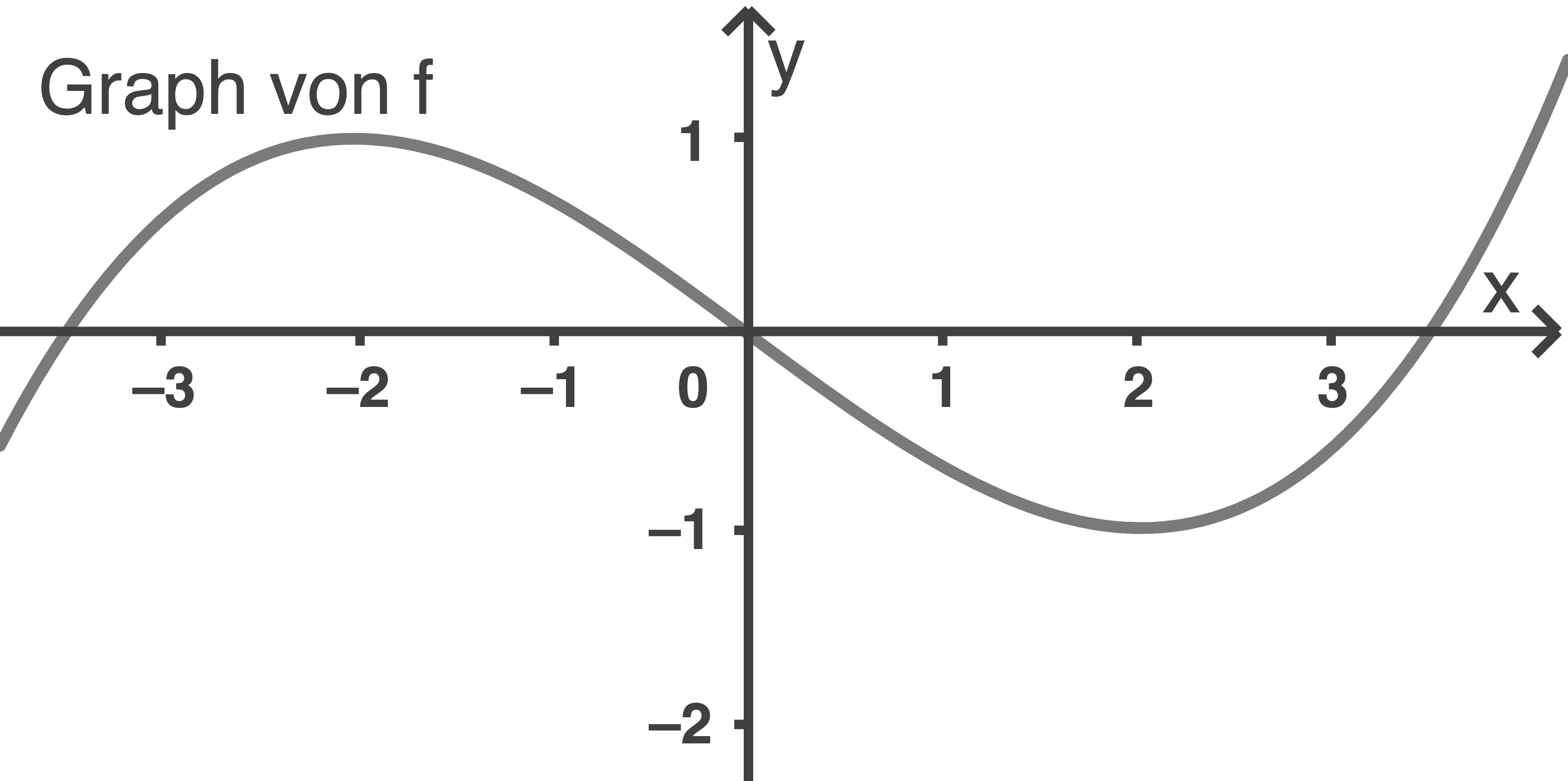 $f.$

Graph einer mathematischen Funktion mit den Achsen x und y.

Einer der folgenden Graphen I, II oder III gehört zur ersten Ableitungsfunktion von $f.$
Gib diesen Graphen an. Begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.

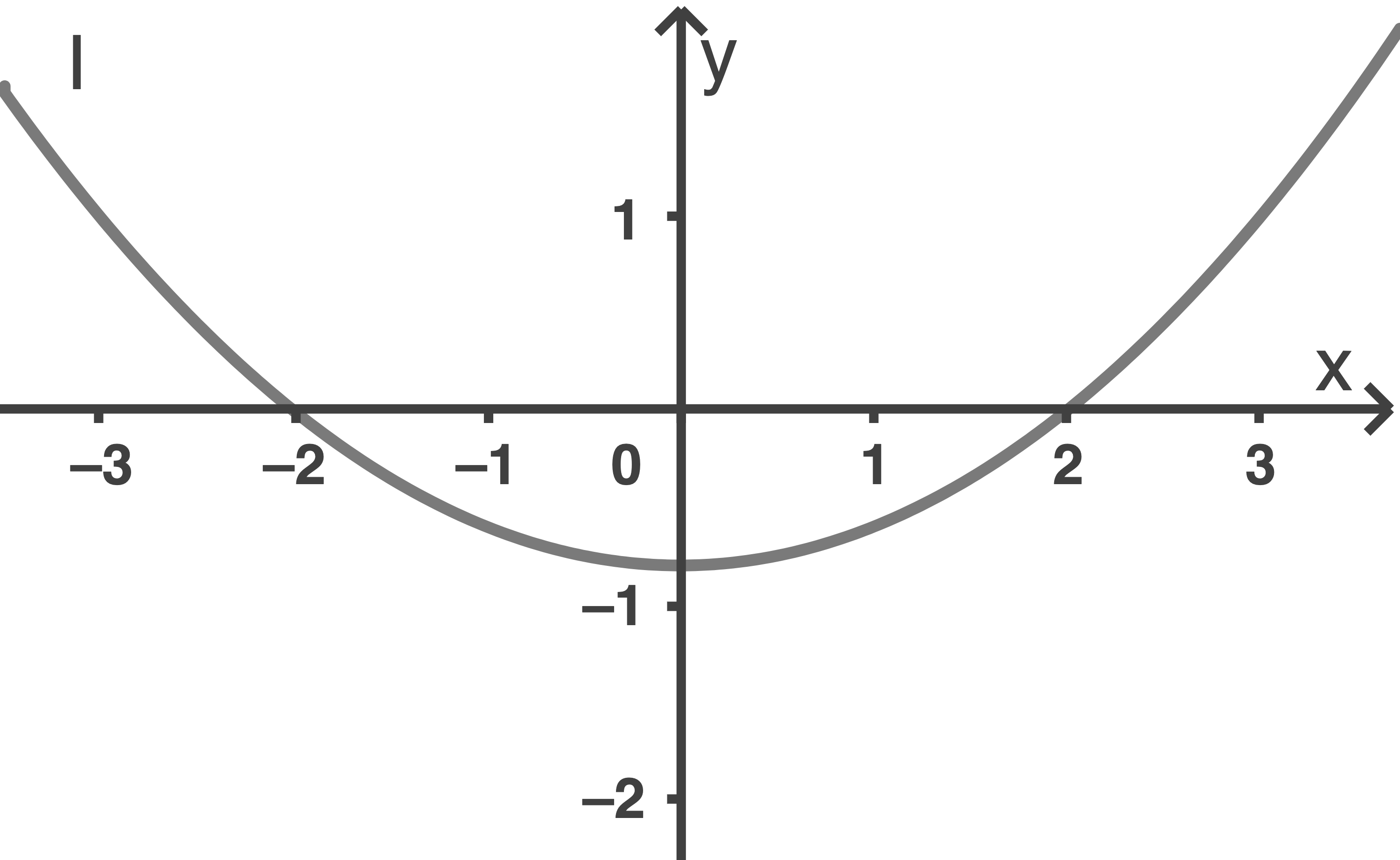
Graf eines Parabelverlaufs mit x- und y-Achse, Zahlen und Koordinatensystem.

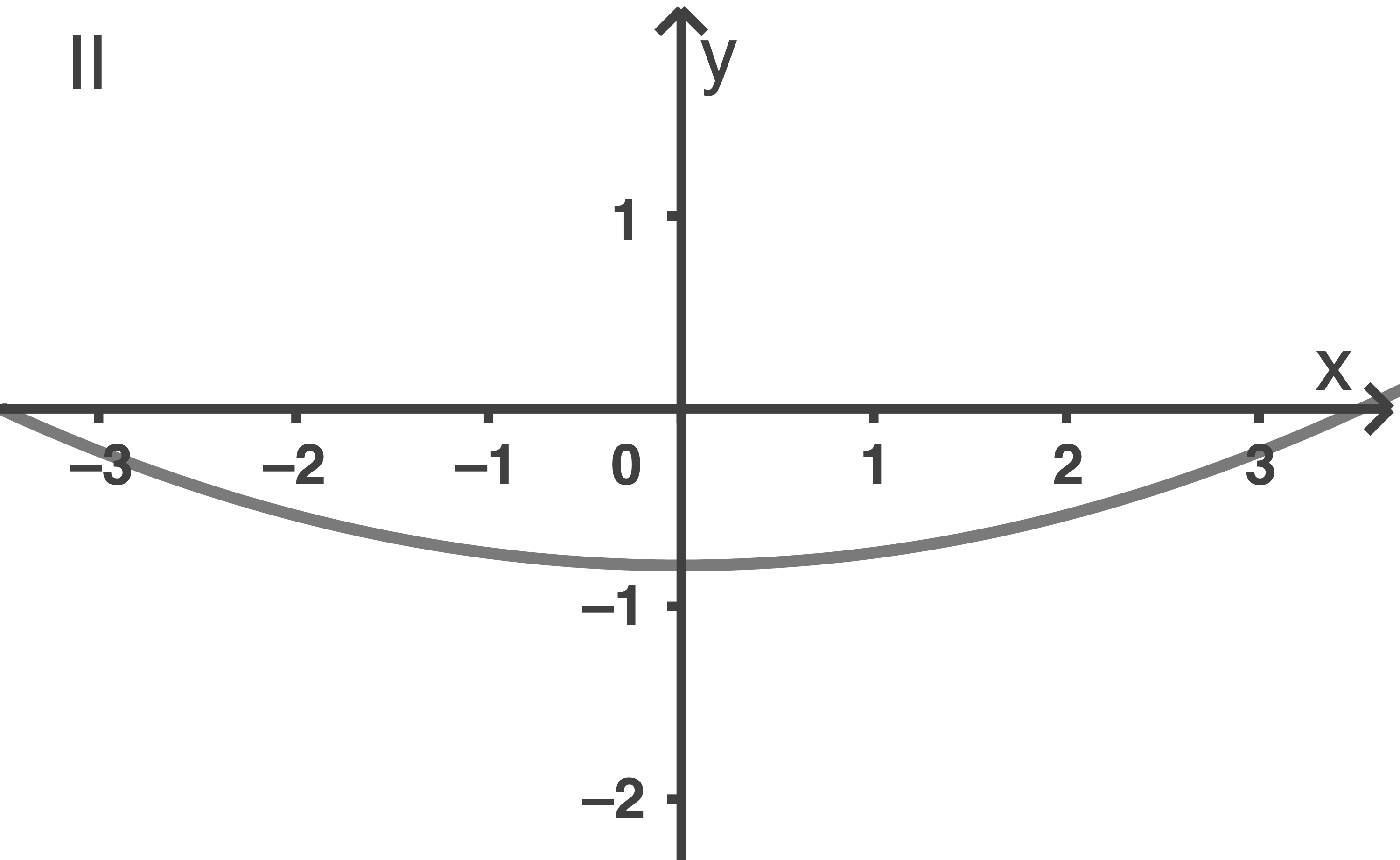
Grafik eines Koordinatensystems mit einer nach oben geöffneten Parabel. Achsen beschriftet mit x und y.

Grafik einer Parabel im Koordinatensystem mit Achsenbezeichnungen.

Die Funktion $F$ ist eine Stammfunktion von $f.$
Gib das Monotonieverhalten von $F$ im Intervall $[1;3]$ an. Begründe deine Angabe.

(2,5 VP)

Aufgabe 5

Gegeben sind die Gerade $g: \overrightarrow{x}= \pmatrix{2\\0\\1}+ t\cdot\pmatrix{1\\0\\-3}$ und die Ebene $E:3x_1-2x_2+x_3=14$ .

Untersuche die gegenseitige Lage von $g$ und $E$ .

Die Gerade $h$ entsteht durch Spiegelung der Geraden $g$ an der Ebene $E$ .
Bestimme eine Gleichung von $h$ .

(4 VP)

Aufgabe 6

Gegeben ist die Gerade $g: \overrightarrow{x}= \pmatrix{4\\-6\\3}+ t\cdot \pmatrix{1\\-2\\2}.$

Berechne die Koordinaten des Punktes, in dem $g$ die $x_2x_3$ -Ebene schneidet.

Bestimme den Abstand des Punktes $P (-3\mid -1 \mid 7)$ von der Geraden $g.$

(4 VP)

Aufgabe 7

In einer Urne sind eine rote, eine weiße und drei schwarze Kugeln. Es wird so lange ohne Zurücklegen gezogen, bis man eine schwarze Kugel zieht.
Berechne die Wahrscheinlichkeit der folgenden Ereignisse:

A: "Man zieht genau zwei Kugeln."
B: "Unter den gezogenen Kugeln befindet sich die rote Kugel."

(3 VP)

Lösung 1

Unter Anwendung der Produkt- und Kettenregel folgt:

$\(f$

Lösung 2

$\begin{array}[t]{rll} (\cos(x))^2+2\cos(x)&=&0\\[5pt] \cos(x)\cdot\left(\cos(x)+2\right) &=&0 \end{array}$

Wegen dem Satz vom Nullprodukt muss mindestens einer der beiden Faktoren Null sein.

$\begin{array}[t]{rll} \text{I}\;&\cos(x)&=&0\\[5pt] \text{II}\;&\cos(x)+2&=&0& \scriptsize\mid\;-2\\[5pt] &\cos(x)&=&-2 \end{array}$

Aus $\text{I}$ folgt: $x_1= \frac{\pi}{2}$ und $x_2=\frac{3}{2}\pi$

Da $\cos(x)$ nur Werte zwischen $-1$ und $1$ annehmen kann, gibt es keine Lösung für die zweite Gleichung.

$\mathbb{L}=\left\{x_1=\dfrac{\pi}{2};x_2=\dfrac{3}{2}\pi\right\}$

Lösung 3

Schnittstelle zeigen

Damit sich die Graphen von $f$ und $g$ an der Stelle $x$ schneiden, muss $f(x) = -3$ gelten:

$\begin{array}[t]{rll} f(x)&=&-3 \\[5pt] 1-\dfrac{1}{x^2} &=& -3\quad \scriptsize \mid\; +3 \\[5pt] 4-\dfrac{1}{x^2} &=& 0\quad \scriptsize \mid\; +\dfrac{1}{x^2} \\[5pt] 4&=& \dfrac{1}{x^2}\quad \scriptsize \mid\; \cdot x^2 \\[5pt] 4x^2&=& 1 \quad \scriptsize \mid\; :4 \\[5pt] x^2 &=& \dfrac{1}{4} \\[5pt] x_1 &=& -\dfrac{1}{2} \\[5pt] x_2 &=& \dfrac{1}{2} \end{array}$

Damit ist gezeigt, dass einer der beiden Punkte die $x$ -Koordinate $\frac{1}{2}$ hat.

Flächeninhalt rechnerisch bestimmen

Die Fläche setzt sich zusammen aus den beiden dunkel bzw. grün gefärbten Flächen zwischen dem Graphen von $f$ und der $x$ -Achse, die aufgrund der Symmetrie von $f$ zur $y$ -Achse gleich groß sind, sowie dem hell gefärbten Rechteck dazwischen mit den Seitenlängen $1$ und $3.$

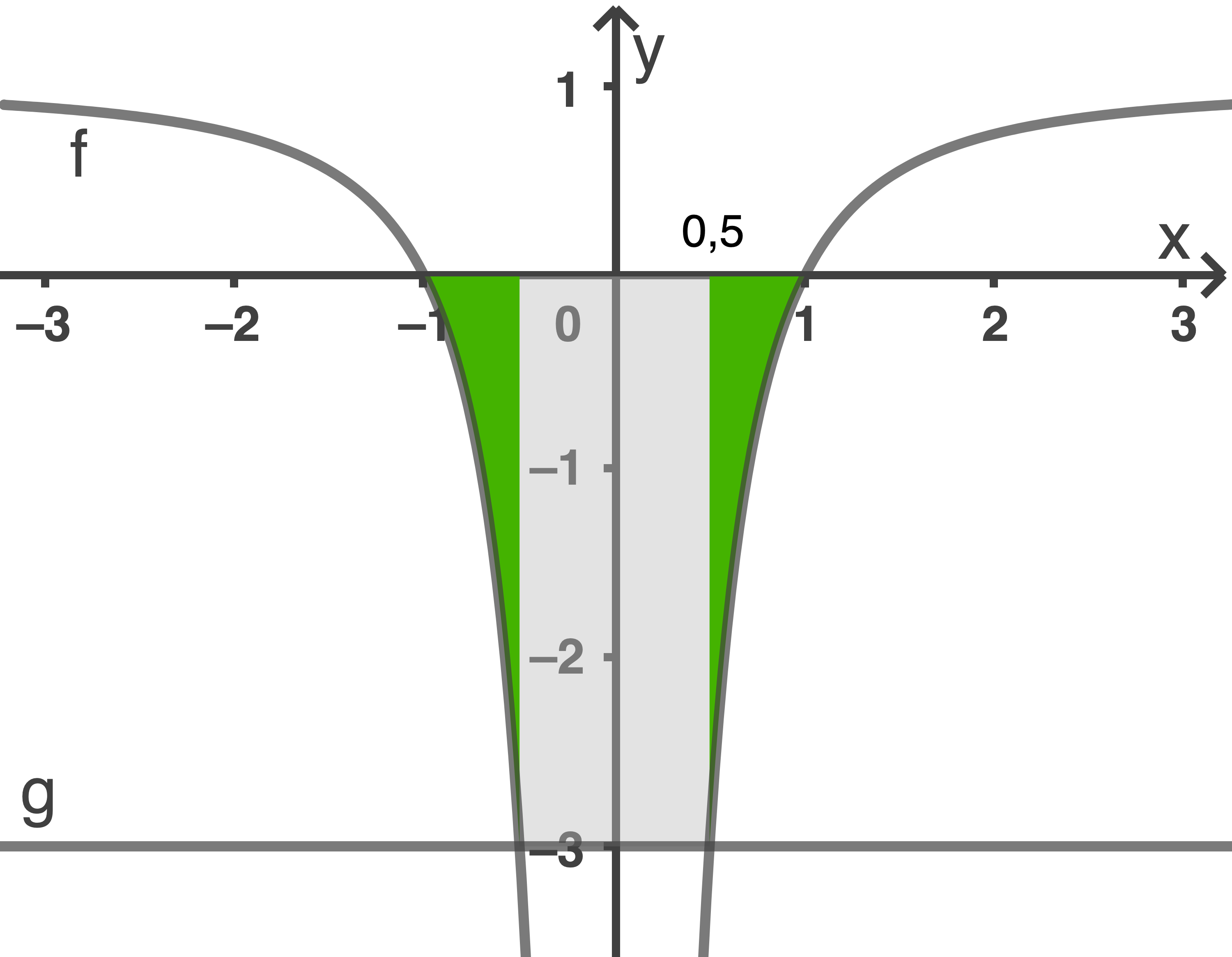Grafische Darstellung einer Funktion mit farbigen Bereichen im Koordinatensystem.

Die Teilflächen liegen unterhalb der $x$ -Achse. Für den Inhalt der Gesamtfläche gilt:

$\begin{array}[t]{rll} A &=& 3\cdot 1 + 2\cdot\left|\displaystyle\int_{0,5}^{1}f(x)\;\mathrm dx \right| \\[5pt] &=& 3\cdot 1 -2\cdot\displaystyle\int_{0,5}^{1}f(x)\;\mathrm dx \\[5pt] &=&3-2\cdot\displaystyle\int_{0,5}^{1}\left(1-\frac{1}{x^2} \right)\;\mathrm dx \\[5pt] &=&3- 2\cdot \left[x+\dfrac{1}{x} \right]_{0,5}^1 \\[5pt] &=&3- 2\cdot\left(1+\dfrac{1}{1} - \left(0,5+\dfrac{1}{0,5} \right)\right)\\[5pt] &=&3+ 1=4 \end{array}$

Die Fläche hat einen Inhalt von $A=4\,\text{FE}.$

Lösung 4

Graph zuordnen

Graph $\text{I}$ gehört zur Ableitungsfunktion $\(f$

Graph $\text{II}$ kann es nicht sein, da an den Stellen $x_1=-2$ und $x_2=2$ die Extremstellen von $f$ liegen und die Ableitungsfunktion $\(f$ an diesen Stellen die $x$ -Achse schneiden muss.
Die Steigung von $f$ an der Stelle $0$ liegt zwischen $0$ und $-1.$ Daher scheidet auch Graph $\text{III}$ aus.

Monotonieverhalten angeben

Laut Abbildung gilt $\(F$ für $1\leq x \leq 3.$
Die Stammfunktion von $F$ ist damit im Intervall streng monoton fallend.

Lösung 5

Gegenseitige Lage untersuchen

Die Punkte auf $g$ besitzen die Koordinaten $G(2+t\mid 0 \mid 1-3t).$ Einsetzen in die Ebenengleichung liefert:

$\begin{array}[t]{rll} 3x_1 -2x_2 +x_3 &=& 14 \\[5pt] 3\cdot (2+t) -2\cdot 0 + (1-3t)&=& 14 \\[5pt] 6+3t +1-3t &=& 14 \\[5pt] 7 &=& 14 \end{array}$

Dies ist ein Widerspruch. Die Gerade $g$ und die Ebene $E$ haben somit keine gemeinsamen Punkte und verlaufen parallel zueinander.

Geradengleichung bestimmen

$h$ verläuft parallel zu $g.$ Der Richtungsvektor von $g$ kann deshalb als Richtungsvektor für $h$ verwendet werden.

Um einen Stützpunkt $\(P$ für $h$ zu erhalten, wird der Stützpunkt $P(2\mid 0\mid 1)$ von $g$ an der Ebene gespiegelt:

1. Schritt: Hilfsgerade aufstellen

Es wird eine Hilfsgerade $k$ aufgestellt, die senkrecht zu $E$ und durch den Stützpunkt $P$ von $g$ verläuft. Als Richtungsvektor wird ein Normalenvektor von $E$ verwendet.

$k:\overrightarrow{x}= \pmatrix{2\\0\\1} + r\cdot \pmatrix{3\\-2\\1}$

2. Schritt: Schnittpunkt bestimmen

Die Koordinaten der Punkte auf der Hilfsgeraden lauten $K(2+3r\mid -2r \mid 1+r).$ Einsetzen in die Ebenengleichung liefert:

$\begin{array}[t]{rll} 3x_1 -2x_2+x_3 &=& 14 \\[5pt] 3\cdot (2+3r) -2\cdot (-2r) + 1+r &=& 14 \\[5pt] 6 +9r +4r +1+r &=& 14 \\[5pt] 7 +14r &=& 14 \\[5pt] 14r &=& 7 \\[5pt] r &=& \dfrac{1}{2} \end{array}$

Einsetzen in die Geradengleichung:

$\overrightarrow{OS} = \pmatrix{2\\0\\1} + \dfrac{1}{2}\cdot \pmatrix{3\\-2\\1} = \pmatrix{3,5\\-1\\1,5}$

3. Schritt: Ortsvektor von $\(P$ bestimmen

Für den gespiegelten Punkt $\(P$ gilt:

$\(\overrightarrow{OP$ $= \pmatrix{2\\0\\1} + 2\cdot \pmatrix{3,5-2\\-1-0\\1,5-1}\,$ $= \pmatrix{2\\0\\1} + 2\cdot \pmatrix{1,5\\-1\\0,5}\,$ $=\pmatrix{5\\-2\\2}$

Eine Gleichung der gespiegelten Gerade lautet:

$h:\overrightarrow{x}=\pmatrix{5\\-2\\2} + t\cdot \pmatrix{1\\0\\-3}$

Lösung 6

Koordinaten des Schnittpunkts berechnen

Damit die Gerade $g$ die $x_2x_3$ -Ebene schneiden kann, muss $x_1=0$ sein. Für die $x_1$ -Koordinate von $g$ gilt $x_1 = 4+t.$

$\begin{array}[t]{rll} 4+t &=& 0\\[5pt] t &=& -4 \end{array}$

Einsetzen in $g$ ergibt den Schnittpunkt:

$\pmatrix{4\\-6\\3} -4 \cdot \pmatrix{1\\-2\\2} = \pmatrix{0 \\ 2 \\ -5}$

Der Schnittpunkt von $g$ mit der $x_2x_3$ -Ebene ist $S(0\mid 2\mid -5).$

Abstand des Punkts bestimmen

1. Schritt: Aufstellen einer Hilfsebene

Die Hilfsebene $H$ steht senkrecht zu $g$ und enthält den Punkt $P.$ Als Normalenvektor wird der Richtungsvektor von $g$ verwendet.

$\begin{array}[t]{rll} x_1 -2x_2 +2x_3 &=& d \\[5pt] -3 -2\cdot (-1) +2\cdot 7 &=& d \\[5pt] 13 &=& d \end{array}$

$H:\, x_1 -2x_2 +2x_3 = 13$

2. Schritt: Schnittpunkt von $H$ und $g$ bestimmen

Die Koordinaten der Punkte auf $g$ lauten $G(4+t \mid -6 -2t \mid 3+2t).$
Einsetzen in die Ebenengleichung von $H$ :

$\begin{array}[t]{rll} x_1 -2x_2 +2x_3 &=& 13 \\[5pt] 4+t - 2(-6-2t) +2(3+2t) &=& 13 \\[5pt] 4+t +12+4t +6 +4t &=& 13 \\[5pt] 22 +9t &=& 13 \\[5pt] 9t &=& -9 \\[5pt] t&=& -1 \end{array}$

Einsetzen in die Geradengleichung liefert:

$\overrightarrow{OS} = \pmatrix{4\\-6\\3} -1\cdot \pmatrix{1\\-2\\2} = \pmatrix{3\\-4\\1}$

3. Schritt: Abstand berechnen

$d(P,g) = \left|\overrightarrow{PS} \right|\,$ $= \left|\pmatrix{6\\-3\\-6} \right| = \sqrt{6^2 +(-3)^2 +(-6)^2} = 9$

Der Punkt $P$ hat von der Geraden $g$ einen Abstand von $9\,\text{LE}.$

Lösung 7

$\begin{array}[t]{rll} P(A) &=& \dfrac{2}{5} \cdot \dfrac{3}{4}=\dfrac{3}{10} \\[5pt] \end{array}$

$P(B)=P(\text{rs})+P(\text{rws})+P(\text{wrs})\,$ $=\dfrac{1}{5}\cdot\dfrac{3}{4}+\dfrac{1}{5}\cdot\dfrac{1}{4}\cdot\dfrac{3}{3}+\dfrac{1}{5}\cdot\dfrac{1}{4}\cdot\dfrac{3}{3}\,$ $=\dfrac{3}{20}+\dfrac{1}{20}+\dfrac{1}{20}\,$ = $\dfrac{5}{20}=\dfrac{1}{4}$