Wahlteil A2
Aufgabe A2.1
Die Anzahl ankommender Fahrzeuge vor einem Grenzübergang soll modelliert werden. Dabei wird die momentane Ankunftsrate beschrieben durch die Funktion  mit
mit

 (
( in Stunden nach Beobachtungsbeginn,
in Stunden nach Beobachtungsbeginn,  in Fahrzeuge pro Stunde).
in Fahrzeuge pro Stunde).
Anfangs befinden sich keine Fahrzeuge vor dem Grenzübergang.
Anfangs befinden sich keine Fahrzeuge vor dem Grenzübergang.
a)
Skizziere den Graphen von  .
Wann ist die momentane Ankunftsrate maximal?
Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden ankommen.
.
Wann ist die momentane Ankunftsrate maximal?
Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden ankommen.
(4 VP)
b)
Am Grenzübergang werden die Fahrzeuge möglichst schnell abgefertigt, jedoch ist die momentane Abfertigungsrate durch  Fahrzeuge pro Stunde begrenzt.
Wann beginnen sich die Fahrzeuge vor dem Grenzübergang zu stauen?
Wie viele Fahrzeuge stauen sich maximal vor dem Grenzübergang?
Welches Ergebnis erhielte man, wenn die momentane Abfertigungsrate
Fahrzeuge pro Stunde begrenzt.
Wann beginnen sich die Fahrzeuge vor dem Grenzübergang zu stauen?
Wie viele Fahrzeuge stauen sich maximal vor dem Grenzübergang?
Welches Ergebnis erhielte man, wenn die momentane Abfertigungsrate  Stunden nach Beobachtungsbeginn auf konstant
Stunden nach Beobachtungsbeginn auf konstant  Fahrzeuge pro Stunde erhöht würde?
Fahrzeuge pro Stunde erhöht würde?
(6 VP)
Aufgabe A2.2
Für jedes  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch

 .
Der Graph von
.
Der Graph von  ist
ist  .
.
 besitzt einen Extrempunkt.
Bestimme dessen Koordinaten.
besitzt einen Extrempunkt.
Bestimme dessen Koordinaten.
a)
(2 VP)
b)
Durch welche Punkte der  -Achse verläuft kein Graph
-Achse verläuft kein Graph  ?
?
(3 VP)
Lösung A2.1
a)  Graphen von
Graphen von  skizzieren
Die Funktion
skizzieren
Die Funktion  beschreibt die momentane Ankunftsrate ankommender Fahrzeuge an einem Grenzübergang. Ihr Funktionsterm ist gegeben durch:
beschreibt die momentane Ankunftsrate ankommender Fahrzeuge an einem Grenzübergang. Ihr Funktionsterm ist gegeben durch:
 Dabei sind
Dabei sind  die Stunden nach Beobachtungsbeginn und
die Stunden nach Beobachtungsbeginn und  die Fahrzeuge pro Stunde. Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang.
die Fahrzeuge pro Stunde. Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang.
Deine Aufgabe ist es, den Graphen der Funktion im Intervall
im Intervall ![\(\left[ 0;30 \right]\)](https://mathjax.schullv.de/975ae5b378f293adfb2e5458c50c0575ac8d05a2c2d23dbe151042c566cabcd7?color=5a5a5a) zu skizzieren. Dabei kannst du folgendermaßen vorgehen:
zu skizzieren. Dabei kannst du folgendermaßen vorgehen:
 Das Schaubild
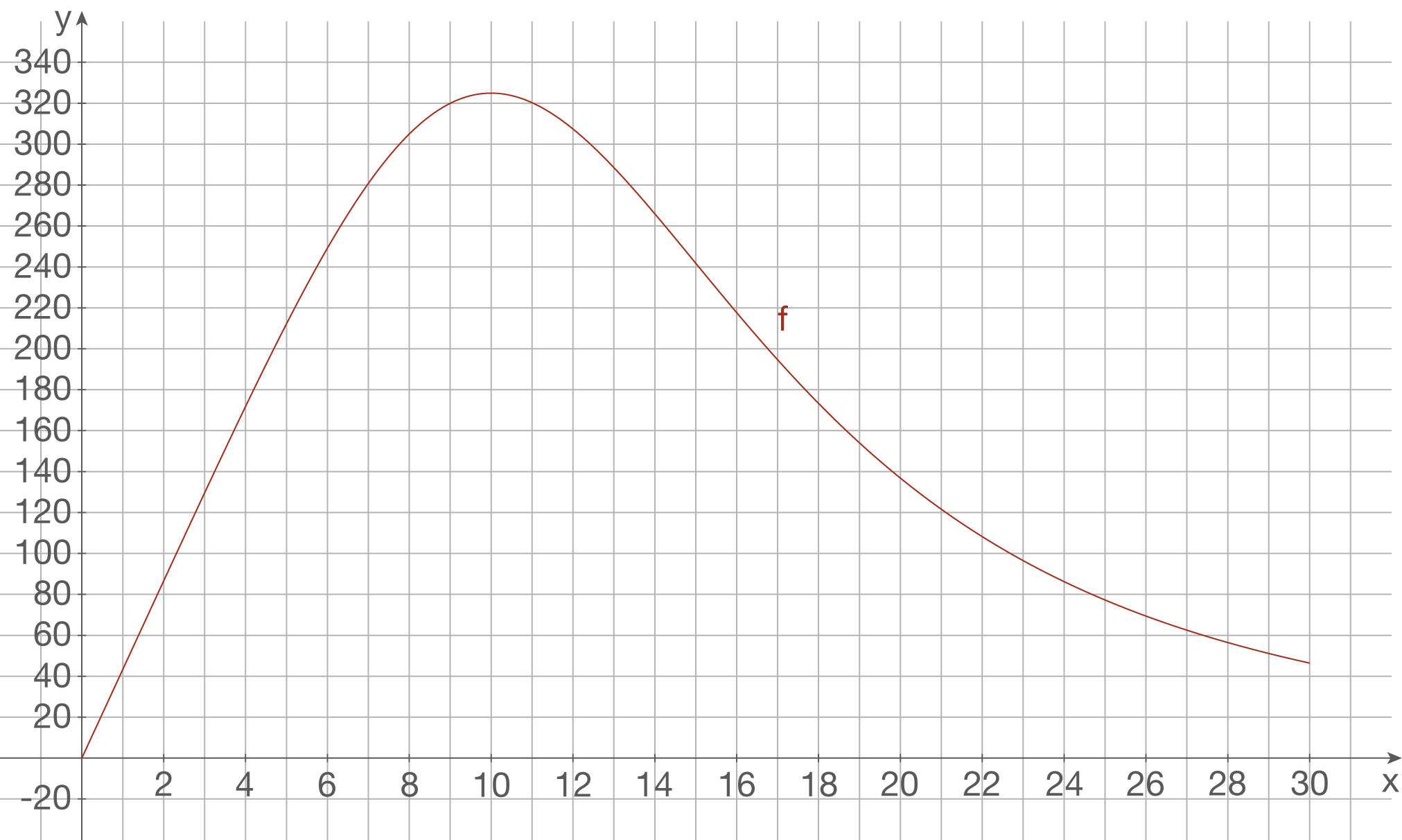
Das Schaubild  sollte dann folgendermaßen aussehen:
sollte dann folgendermaßen aussehen:
 Maximale momentane Ankunftsrate bestimmen
Die Funktion
Maximale momentane Ankunftsrate bestimmen
Die Funktion  beschreibt die momentane Ankunftsrate von Fahrzeugen pro Stunde. Um die maximale momentane Ankunftsrate zu ermitteln, kannst du zunächst das Maximum der Funktion
beschreibt die momentane Ankunftsrate von Fahrzeugen pro Stunde. Um die maximale momentane Ankunftsrate zu ermitteln, kannst du zunächst das Maximum der Funktion  mit dem GTR bestimmen. Prüfe, ob es Randextrema gibt.
mit dem GTR bestimmen. Prüfe, ob es Randextrema gibt.
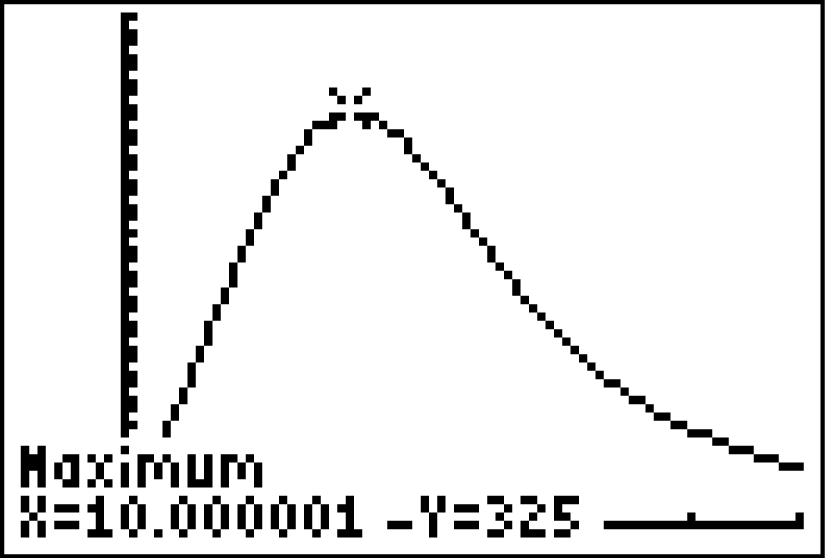 Die Koordinaten des Hochpunktes kannst du mit deinem GTR berechnen. Lasse dir dazu zunächst den Graphen der Funktion für
Die Koordinaten des Hochpunktes kannst du mit deinem GTR berechnen. Lasse dir dazu zunächst den Graphen der Funktion für  zeichnen. Das Maximum kannst du dir mit folgendem Befehl berechnen lassen:
zeichnen. Das Maximum kannst du dir mit folgendem Befehl berechnen lassen:
Anhand des Graphen siehst du, dass die Funktion kein weiteres Maximum an den Intervallgrenzen hat. Du kannst jedoch zusätzlich die Funktionswerte an den Stellen  und
und  mit dem GTR berechnen. Sind diese kleiner als der Funktionswert des Hochpunktes, so hat die Funktion
mit dem GTR berechnen. Sind diese kleiner als der Funktionswert des Hochpunktes, so hat die Funktion  keine Maxima an den Intervallgrenzen.
Die Koordinaten des Hochpunktes
keine Maxima an den Intervallgrenzen.
Die Koordinaten des Hochpunktes  lauten
lauten  . Die maximale momentane Ankunftsrate beträgt demnach 325 Fahrzeuge pro Stunde.
. Die maximale momentane Ankunftsrate beträgt demnach 325 Fahrzeuge pro Stunde.
 Anzahl der Fahrzeuge bestimmen, die in den ersten 6 Stunden ankommen
Beschreibt die Funktion
Anzahl der Fahrzeuge bestimmen, die in den ersten 6 Stunden ankommen
Beschreibt die Funktion  die momentane Ankunftsrate, so entspricht ihre Stammfunktion
die momentane Ankunftsrate, so entspricht ihre Stammfunktion  der Anzahl der ankommenden Fahrzeuge. Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden am Grenzübergang ankommen. Diese Anzahl erhältst du über folgenden Zusammenhang:
der Anzahl der ankommenden Fahrzeuge. Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden am Grenzübergang ankommen. Diese Anzahl erhältst du über folgenden Zusammenhang:
 Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang. Daher ist die Konstante, die sich bei der Integration ergibt, gleich Null.
Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang. Daher ist die Konstante, die sich bei der Integration ergibt, gleich Null.
Das Integral über das Intervall![\(\left[0;6\right]\)](https://mathjax.schullv.de/4f9e3c1911b7f2eaf5dc78df3b762538d9382a576594ceb6550206df6c41ba48?color=5a5a5a) kannst du mit Hilfe des GTR bestimmen.
kannst du mit Hilfe des GTR bestimmen.
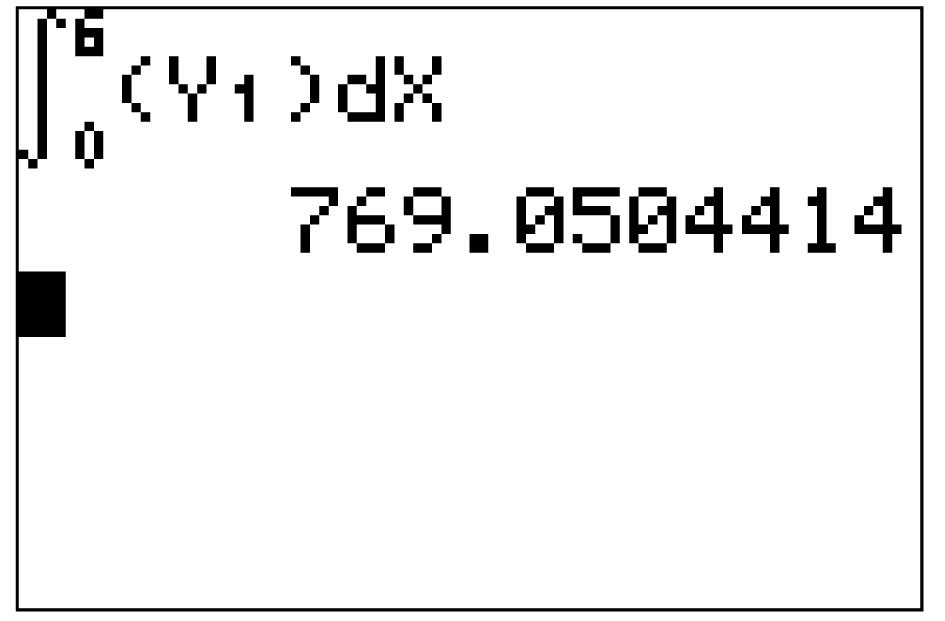 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Gib die Integrationsgrenzen und den Integranden an. Diesen erhältst du über die folgende Befehlsfolge:
Wähle in diesem Menü dann die entsprechende Funktion  aus, unter welcher du den Term von
aus, unter welcher du den Term von  abgespeichert hast.
Der GTR liefert dir, dass ungefähr 769 Fahrzeuge in den ersten 6 Stunde am Grenzübergang ankommen.
abgespeichert hast.
Der GTR liefert dir, dass ungefähr 769 Fahrzeuge in den ersten 6 Stunde am Grenzübergang ankommen.
Deine Aufgabe ist es, den Graphen der Funktion
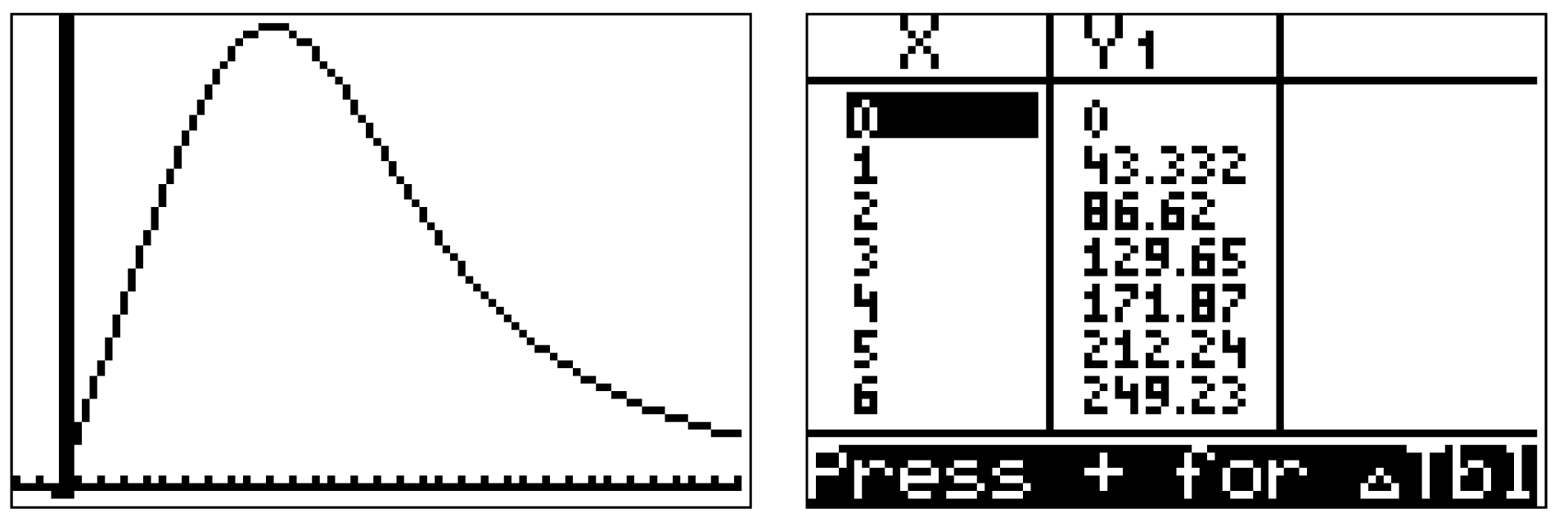
- Betrachte das Schaubild in deinem GTR, indem du den Graph-Modus auswählst.
- Lasse dir die zugehörige Wertetabelle der Funktion einblenden. Diese findest du im Graph-Modus unter TABLE :



|
2ND |
Das Integral über das Intervall
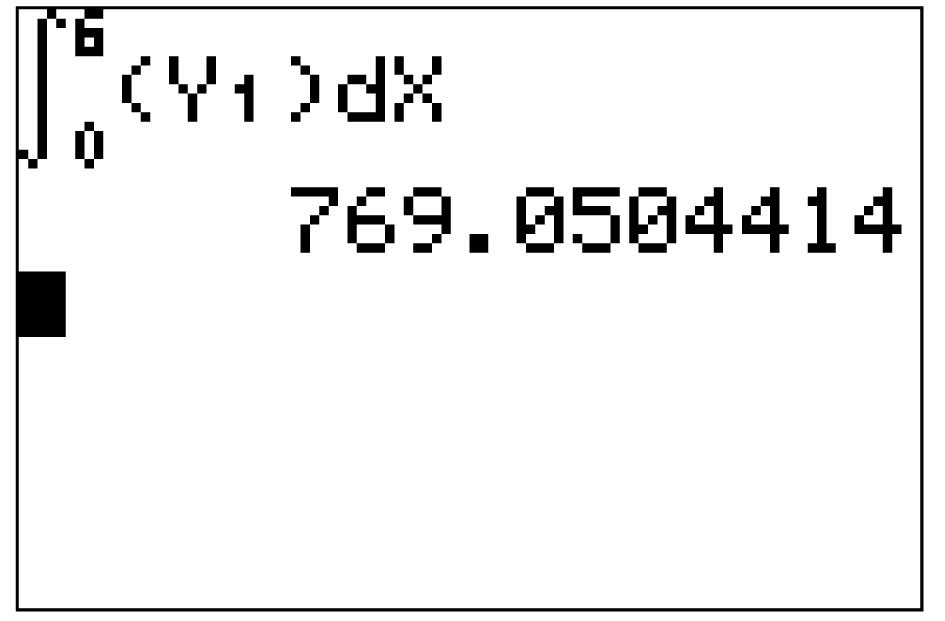
|
MATH |
b)  Zeitpunkt bestimmen, an dem sich erstmals Fahrzeuge stauen
Pro Stunde können am Grenzübergang
Zeitpunkt bestimmen, an dem sich erstmals Fahrzeuge stauen
Pro Stunde können am Grenzübergang  Fahrzeuge abgefertigt werden. Aus dem Aufgabenteil zuvor weißt du jedoch, dass die maximale momentane Ankunftsrate 325 Fahrzeuge pro Stunde beträgt. Das heißt, dass zu einem gewissen Zeitpunkt mehr Fahrzeuge am Grenzübergang ankommen als abgefertigt werden können.
Fahrzeuge abgefertigt werden. Aus dem Aufgabenteil zuvor weißt du jedoch, dass die maximale momentane Ankunftsrate 325 Fahrzeuge pro Stunde beträgt. Das heißt, dass zu einem gewissen Zeitpunkt mehr Fahrzeuge am Grenzübergang ankommen als abgefertigt werden können.
Deine Aufgabe ist es, diesen Zeitpunkt zu bestimmen. Dabei kannst du wie folgt vorgehen:
zu bestimmen. Dabei kannst du wie folgt vorgehen:
 und der Geraden
und der Geraden  im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem
im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem  den Funktionswert 110 erreicht.
den Funktionswert 110 erreicht.
 Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit Enter liefert dir zwei verschiedene Resultate:
Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit Enter liefert dir zwei verschiedene Resultate:
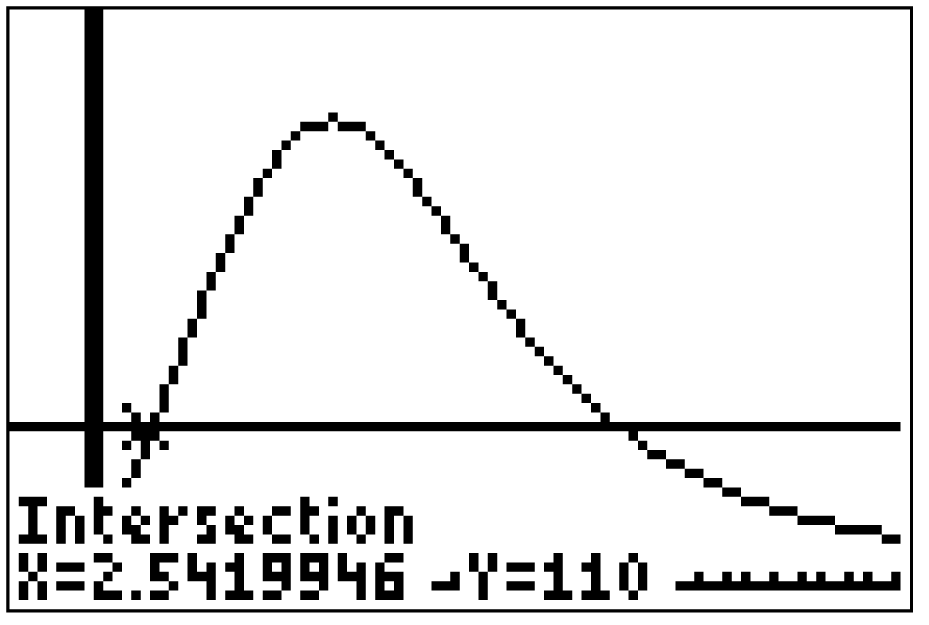
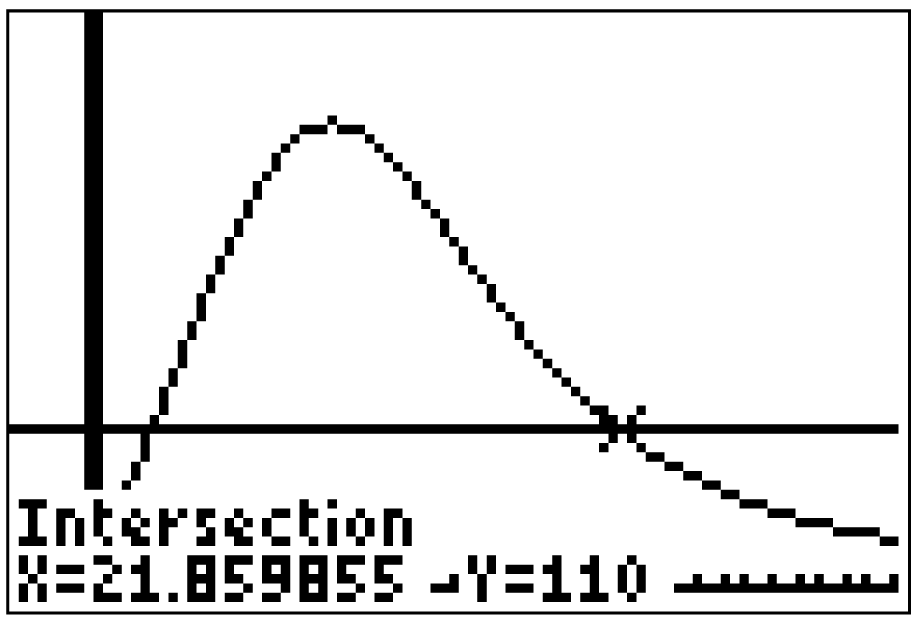 Anhand des Graphen der Funktion
Anhand des Graphen der Funktion  kannst du erkennen, dass an
kannst du erkennen, dass an  erstmalig die Anzahl von 110 pro Stunde ankommenden Fahrzeugen überschritten wird. Das liefert dir, dass der gesuchte Zeitpunkt
erstmalig die Anzahl von 110 pro Stunde ankommenden Fahrzeugen überschritten wird. Das liefert dir, dass der gesuchte Zeitpunkt  ist.
ist.
Nach 2,54 Stunden beginnen sich Fahrzeuge vor dem Grenzübergang zu stauen. Anzahl der Fahrzeuge ermitteln, die sich vor dem Übergang stauen
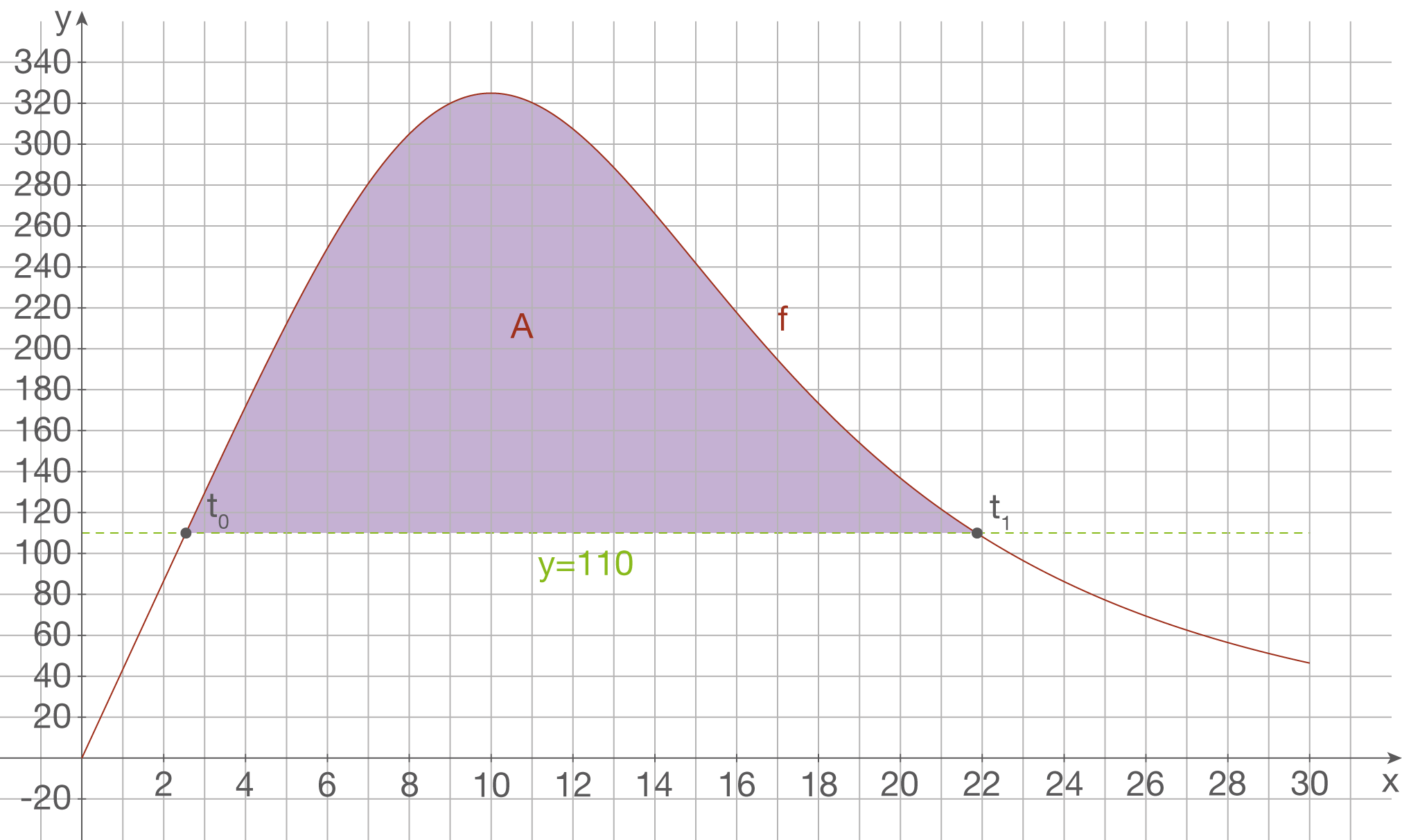
In der Abbildung unten siehst du den skizzierten Graphen der Funktion
Anzahl der Fahrzeuge ermitteln, die sich vor dem Übergang stauen
In der Abbildung unten siehst du den skizzierten Graphen der Funktion  und der Geraden
und der Geraden  . Zuvor hast du ermittelt, dass sich erstmalig zum Zeitpunkt
. Zuvor hast du ermittelt, dass sich erstmalig zum Zeitpunkt  Fahrzeuge vor dem Übergang stauen. Die Anzahl
Fahrzeuge vor dem Übergang stauen. Die Anzahl  der Fahrzeuge, die sich maximal vor dem Übergang anstauen, entspricht der rot markierten Fläche:
der Fahrzeuge, die sich maximal vor dem Übergang anstauen, entspricht der rot markierten Fläche:
 Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
 Dabei sind
Dabei sind  und
und  die Schnittstellen der Funktion
die Schnittstellen der Funktion  und der Gerdaden
und der Gerdaden  , die du zuvor bestimmt hast mit:
, die du zuvor bestimmt hast mit:
![\(\left[t_0;t_1\right]\)](https://mathjax.schullv.de/3fd6f5ac2f7bc9960f5df993e2f1f3fdcc14be1502199f30bce421974ae8d077?color=5a5a5a) gewählt, da ab dem Zeitpunkt
gewählt, da ab dem Zeitpunkt  wieder weniger Fahrzeuge ankommen, als abgefertigt werden können. Das heißt, die Anzahl
wieder weniger Fahrzeuge ankommen, als abgefertigt werden können. Das heißt, die Anzahl  nimmt ab.
nimmt ab.
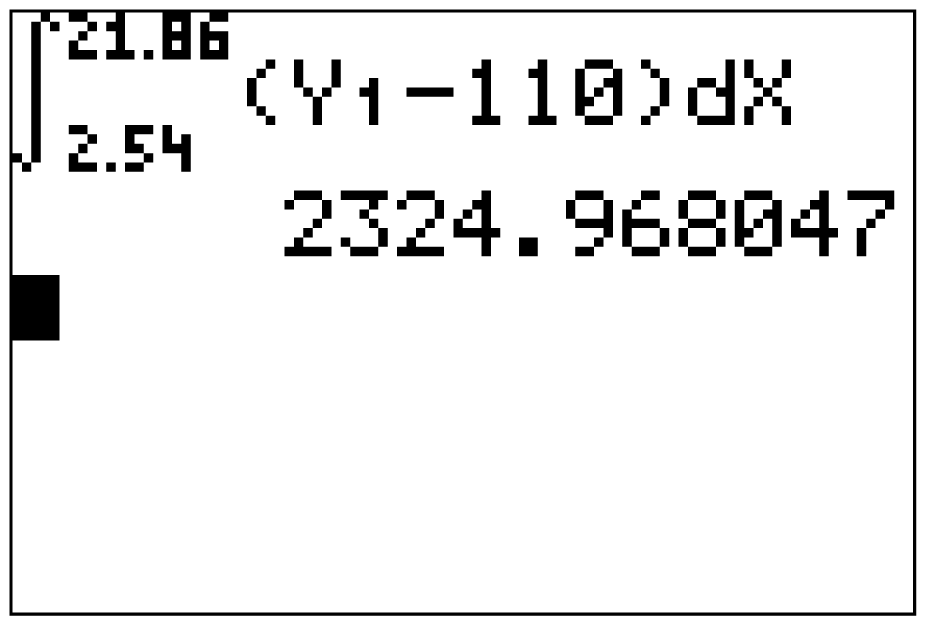
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest.
Das Integral über das Intervall![\(\left[t_0;t_1\right]\)](https://mathjax.schullv.de/3fd6f5ac2f7bc9960f5df993e2f1f3fdcc14be1502199f30bce421974ae8d077?color=5a5a5a) kannst du mit Hilfe des GTR bestimmen.
kannst du mit Hilfe des GTR bestimmen.
 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Gib die Integrationsgrenzen und den Integranden an. Diesen erhältst du über die folgende Befehlsfolge:
Wähle in diesem Menü dann die entsprechende Funktion  aus, unter welcher du den Term von
aus, unter welcher du den Term von  abgespeichert hast.
Der GTR liefert dir, dass sich maximal 2.325 Fahrzeuge am Grenzübergang anstauen.
abgespeichert hast.
Der GTR liefert dir, dass sich maximal 2.325 Fahrzeuge am Grenzübergang anstauen.
 Anzahl bei einer Abfertigungsrate von 220 Fahrzeugen pro Stunde
12 Stunden nach Beobachtungsbeginn soll die momentane Abfertigungsate auf
Anzahl bei einer Abfertigungsrate von 220 Fahrzeugen pro Stunde
12 Stunden nach Beobachtungsbeginn soll die momentane Abfertigungsate auf  Fahrzeuge pro Stunde erhöht werden. In den Stunden davor soll die momentane Abfertigungsrate weiterhin 110 Fahrzeuge pro Stunde betragen.
Fahrzeuge pro Stunde erhöht werden. In den Stunden davor soll die momentane Abfertigungsrate weiterhin 110 Fahrzeuge pro Stunde betragen.
Berechne unter diesen Voraussetzungen die Anzahl der sich anstauenden Fahrzeuge. Die gesuchte Anzahl entspricht hier der rot markierten Fläche.
entspricht hier der rot markierten Fläche.
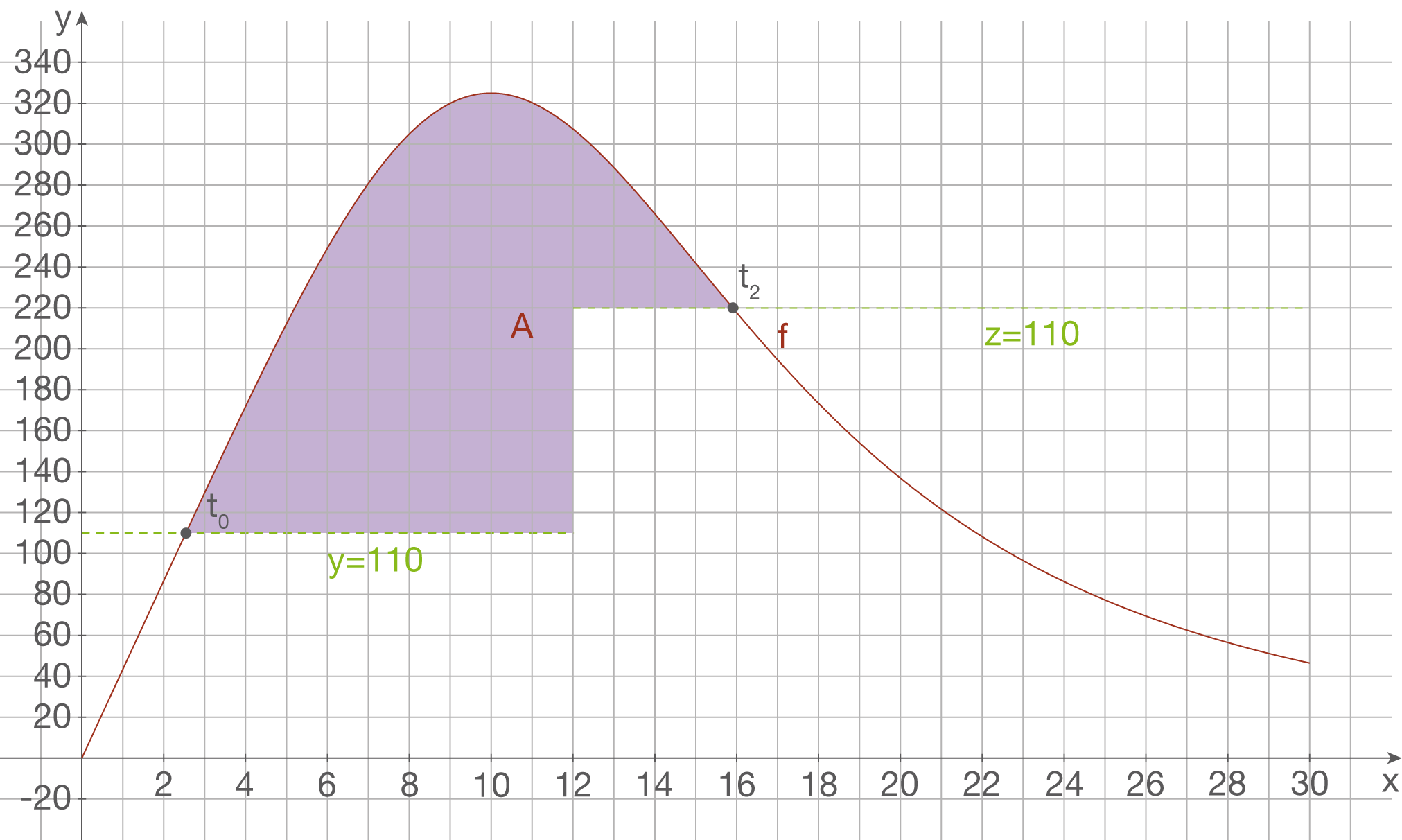 Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
Dabei ist
Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
Dabei ist  die Schnittstelle der Funktion
die Schnittstelle der Funktion  und der Geraden
und der Geraden  , die du zuvor bestimmt hast mit:
, die du zuvor bestimmt hast mit:  .
.
Dahingegen ist die Schnittstelle der Funktion
die Schnittstelle der Funktion  und der Geraden
und der Geraden  . Um die gesuchte Anzahl zu ermitteln, kannst du also wie folgt vorgehen:
. Um die gesuchte Anzahl zu ermitteln, kannst du also wie folgt vorgehen:
 bestimmen
Das kannst du mittels GTR graphisch lösen. Gib dazu den Term der Funktion
bestimmen
Das kannst du mittels GTR graphisch lösen. Gib dazu den Term der Funktion  und der Geraden
und der Geraden  im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem
im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem  den Funktionswert 220 erreicht.
den Funktionswert 220 erreicht.
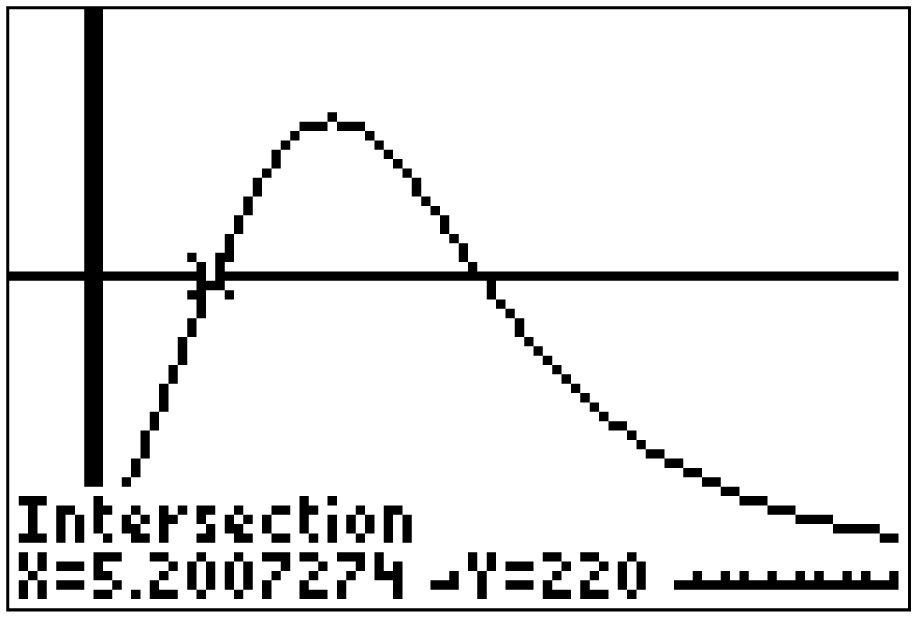 Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit Enter liefert dir zwei verschiedene Resultate:
Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit Enter liefert dir zwei verschiedene Resultate:
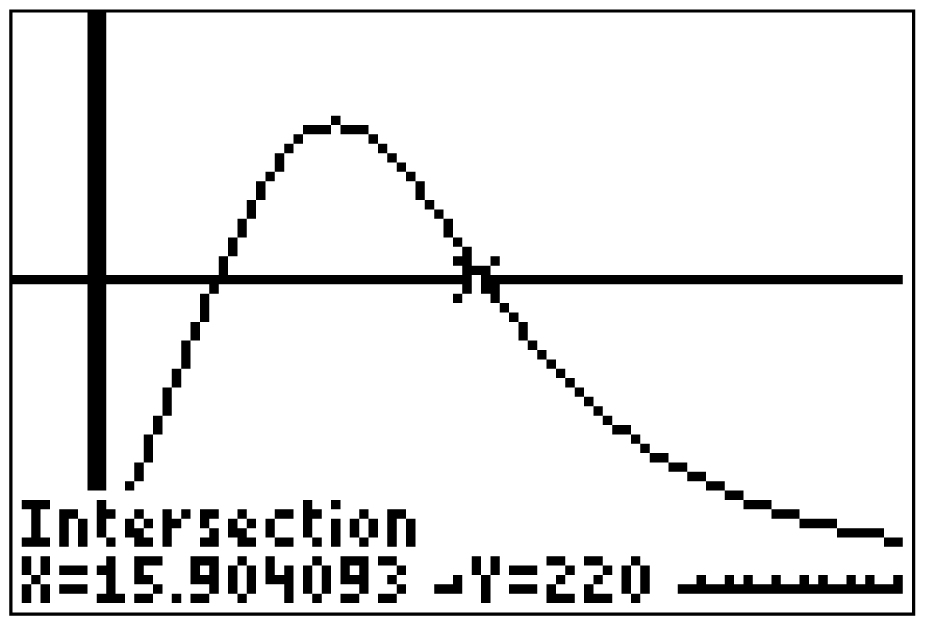 Anhand des Graphen der Funktion
Anhand des Graphen der Funktion  kannst du erkennen, dass an
kannst du erkennen, dass an  erstmalig die Anzahl von 220 pro Stunde ankommenden Fahrzeugen überschritten wird. Da aber erst nach 12 Stunden auf 220 erhöht werden soll, kannst du dieses Resultat vernachlässigen. Das liefert dir, dass der gesuchte Zeitpunkt
erstmalig die Anzahl von 220 pro Stunde ankommenden Fahrzeugen überschritten wird. Da aber erst nach 12 Stunden auf 220 erhöht werden soll, kannst du dieses Resultat vernachlässigen. Das liefert dir, dass der gesuchte Zeitpunkt  ist.
2. Schritt: Anzahl der sich anstauenden Fahrzeuge berechnen
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest. Das Integral
kannst du mit Hilfe des GTR bestimmen.
ist.
2. Schritt: Anzahl der sich anstauenden Fahrzeuge berechnen
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest. Das Integral
kannst du mit Hilfe des GTR bestimmen.
 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Gib die Integrationsgrenzen und den Integranden an. Diesen erhältst du über die folgende Befehlsfolge:
Wähle in diesem Menü dann die entsprechende Funktion  aus, unter welcher du den Term von
aus, unter welcher du den Term von  abgespeichert hast.
abgespeichert hast.
Der GTR liefert dir, dass sich durch die Erhöhung ab der 12. Stunde auf 220 Fahrzeuge pro Stunde maximal Fahrzeuge am Grenzübergang anstauen.
Fahrzeuge am Grenzübergang anstauen.
Deine Aufgabe ist es, diesen Zeitpunkt
- Der Zeitpunkt entspricht der Stelle von
, an der
erstmals den Funktionswert 110 erreicht. Setze also den Term der Funktion
mit 110 gleich.
- Löse nach
auf, um den gesuchten Zeitpunkt zu erhalten.


Nach 2,54 Stunden beginnen sich Fahrzeuge vor dem Grenzübergang zu stauen.

Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest.
Das Integral über das Intervall

|
MATH |
Berechne unter diesen Voraussetzungen die Anzahl der sich anstauenden Fahrzeuge. Die gesuchte Anzahl

Dahingegen ist
- Bestimme die Schnittstelle
der Funktion
und der Geraden
.
- Berechne das Integral



|
MATH |
Der GTR liefert dir, dass sich durch die Erhöhung ab der 12. Stunde auf 220 Fahrzeuge pro Stunde maximal
Lösung A2.2
a)  Koordinaten des Extrempunktes angeben
Die Funktionenschar
Koordinaten des Extrempunktes angeben
Die Funktionenschar  mit
mit  und dem Definitionsbereich
und dem Definitionsbereich  ist durch folgenden Term definiert:
ist durch folgenden Term definiert:
 In der Aufgabenstellung wird angegeben, dass der Graph der Funktionenschar
In der Aufgabenstellung wird angegeben, dass der Graph der Funktionenschar  einen Extrempunkt besitzt. Deine Aufgabe ist es, dessen Koordinaten anzugeben. Beachte, dass diese Koordinaten vom Parameter
einen Extrempunkt besitzt. Deine Aufgabe ist es, dessen Koordinaten anzugeben. Beachte, dass diese Koordinaten vom Parameter  abhängig sein können, da es sich hierbei um eine Funktionenschar handelt.
abhängig sein können, da es sich hierbei um eine Funktionenschar handelt.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion
einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  .
.
 Für die notwendige Bedingung einer Extremstelle muss
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze den Funktionsterm der ersten Ableitung
gelten. Setze den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
 Im ersten Schritt dürfen wir durch
Im ersten Schritt dürfen wir durch  dividieren, da
dividieren, da  Voraussetzung ist.
Voraussetzung ist.
Weiterhin weißt du, dass die Sinusfunktion für den Wert Null annimmt. Da die Funktionenschar
den Wert Null annimmt. Da die Funktionenschar  aber nur im Bereich
aber nur im Bereich  definiert ist, kommt nur
definiert ist, kommt nur  als Nullstelle in Frage.
als Nullstelle in Frage.
Damit hast du eine potentielle Extremstelle an ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut ableitest:
erneut ableitest:
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/b2dc8306491b985c8622106e6b4dccf1a79a1c61f01d1056d1f544a2155370f6?color=5a5a5a) Überprüfe nun, ob
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
 Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist, da
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist, da  gilt. Das heißt, an
gilt. Das heißt, an  liegt eine Extremstelle vor. Wegen
liegt eine Extremstelle vor. Wegen  kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle
kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes ermittelt. Die
-Koordinate des Hochpunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
 Die Koordinaten des Extrempunktes
Die Koordinaten des Extrempunktes  lauten
lauten  .
.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Weiterhin weißt du, dass die Sinusfunktion für
Damit hast du eine potentielle Extremstelle an
b)  Punkte auf der
Punkte auf der  -Achse angeben
-Achse angeben
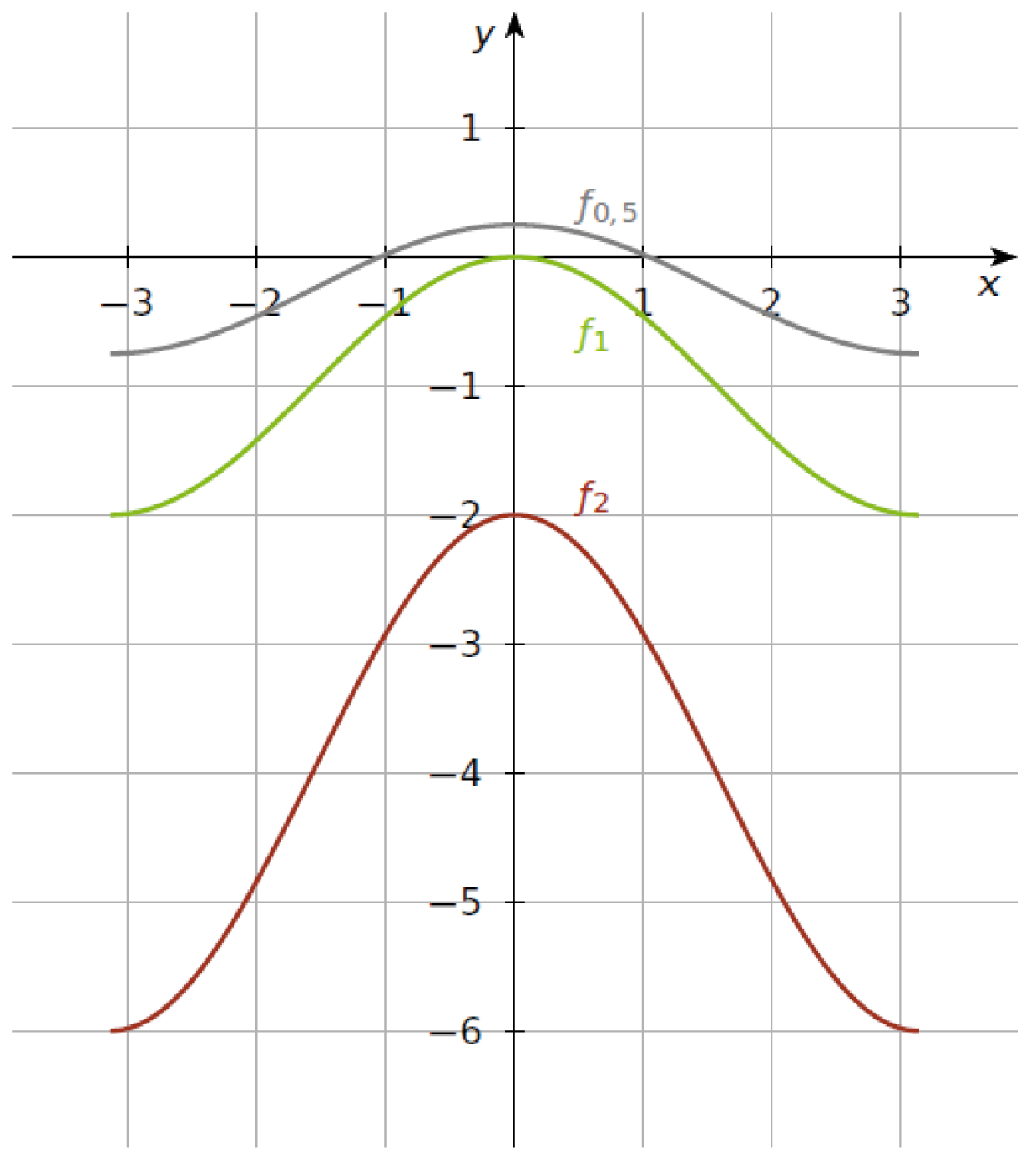 Im Schaubild kannst du erkennen, dass die Graphen der Funktionen
Im Schaubild kannst du erkennen, dass die Graphen der Funktionen  ,
,  und
und  der Funktionenschar
der Funktionenschar  jeweils einen Punkt auf der
jeweils einen Punkt auf der  -Achse schneiden. Gib die Punkte an, durch welche kein Graph der Funktionenschar
-Achse schneiden. Gib die Punkte an, durch welche kein Graph der Funktionenschar  verläuft.
verläuft.
Dabei kannst du folgende Eigenschaften verwenden: mit dem Term
mit dem Term  und der Bedingung
und der Bedingung  .
.
Diese Hilfsfunktion gibt die -Koordinate des Schnittpunktes
-Koordinate des Schnittpunktes  mit der
mit der  -Achse in Abhängigkeit von
-Achse in Abhängigkeit von  an.
an.
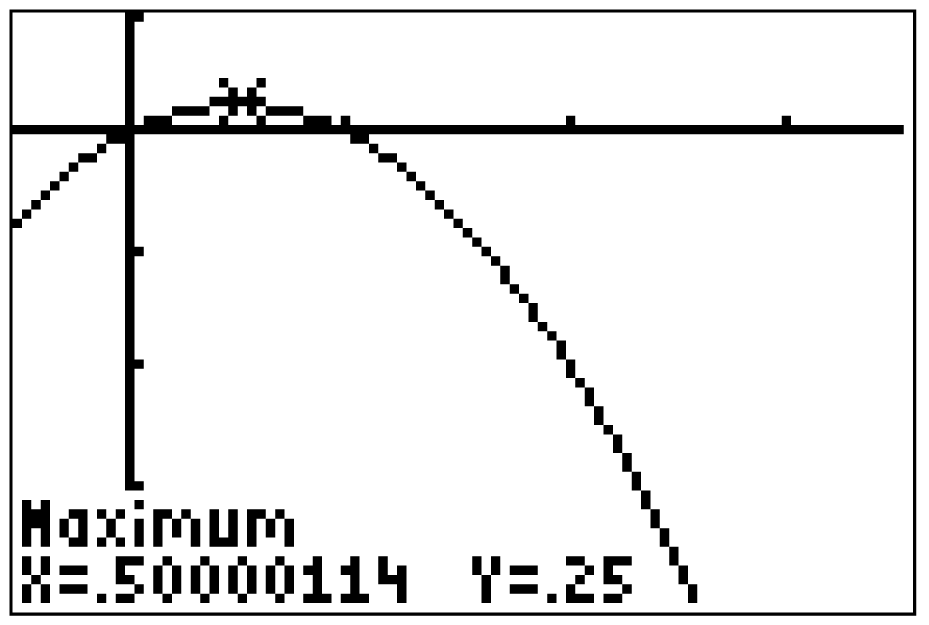 Lässt du die Hilfsfunktion in deinem GTR zeichnen, so kannst du erkennen, dass die Funktion
Lässt du die Hilfsfunktion in deinem GTR zeichnen, so kannst du erkennen, dass die Funktion  nach unten nicht beschränkt ist.
nach unten nicht beschränkt ist.
Ihr Maximum kannst du ermitteln, indem du
auswählst.
Der GTR liefert dir, dass sich das Maximum an mit
mit  befindet. Das heißt, der Extrempunkt bzw. Schnittpunkt mit der
befindet. Das heißt, der Extrempunkt bzw. Schnittpunkt mit der  -Achse kann maximal die
-Achse kann maximal die  -Koordinate
-Koordinate  besitzen.
besitzen.
Du kannst also festhalten, dass der Graph der Funktionenschar die Punkte
die Punkte  auf der
auf der  -Achse nicht berührt, für die
-Achse nicht berührt, für die  gilt.
gilt.

Dabei kannst du folgende Eigenschaften verwenden:
- Laut Aufgabentext muss
gelten.
- Der Extrempunkt besitzt die Koordinaten
und stellt damit den Schnittpunkt mit der
-Achse dar.
Diese Hilfsfunktion gibt die

Ihr Maximum kannst du ermitteln, indem du
|
menu |
Der GTR liefert dir, dass sich das Maximum an
Du kannst also festhalten, dass der Graph der Funktionenschar
Lösung A2.1
a)  Graphen von
Graphen von  skizzieren
Die Funktion
skizzieren
Die Funktion  beschreibt die momentane Ankunftsrate ankommender Fahrzeuge an einem Grenzübergang. Ihr Funktionsterm ist gegeben durch:
beschreibt die momentane Ankunftsrate ankommender Fahrzeuge an einem Grenzübergang. Ihr Funktionsterm ist gegeben durch:
 Dabei sind
Dabei sind  die Stunden nach Beobachtungsbeginn und
die Stunden nach Beobachtungsbeginn und  die Fahrzeuge pro Stunde. Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang.
die Fahrzeuge pro Stunde. Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang.
Deine Aufgabe ist es, den Graphen der Funktion im Intervall
im Intervall ![\(\left[ 0;30 \right]\)](https://mathjax.schullv.de/975ae5b378f293adfb2e5458c50c0575ac8d05a2c2d23dbe151042c566cabcd7?color=5a5a5a) zu skizzieren. Dabei kannst du folgendermaßen vorgehen:
zu skizzieren. Dabei kannst du folgendermaßen vorgehen:
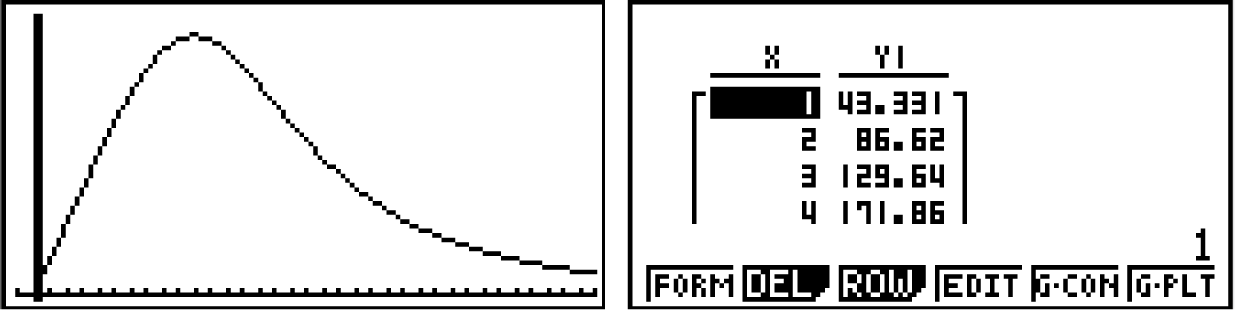 Das Schaubild
Das Schaubild  sollte dann folgendermaßen aussehen:
sollte dann folgendermaßen aussehen:
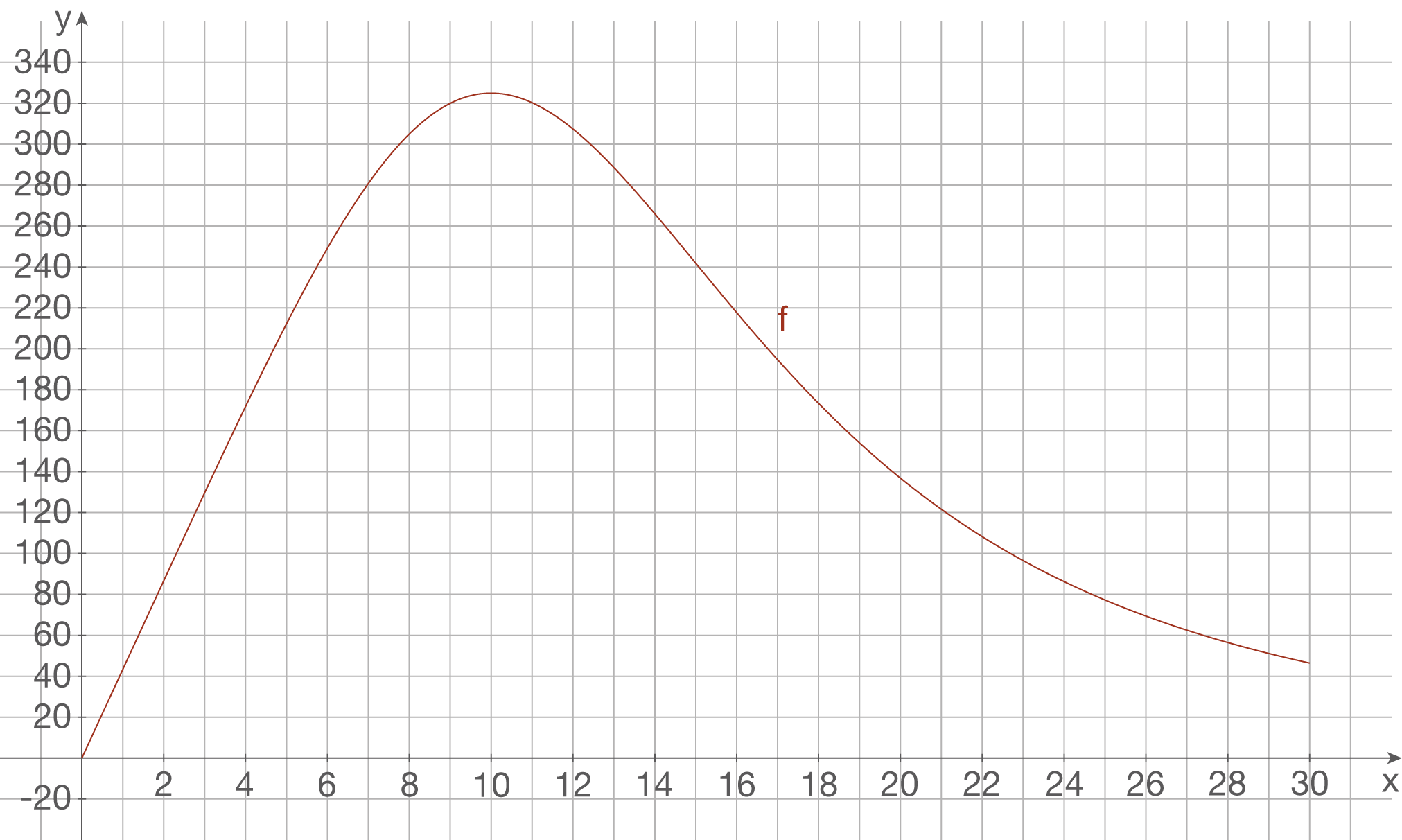
 Maximale momentane Ankunftsrate bestimmen
Die Funktion
Maximale momentane Ankunftsrate bestimmen
Die Funktion  beschreibt die momentane Ankunftsrate von Fahrzeugen pro Stunde. Um die maximale momentane Ankunftsrate zu ermitteln, kannst du zunächst das Maximum der Funktion
beschreibt die momentane Ankunftsrate von Fahrzeugen pro Stunde. Um die maximale momentane Ankunftsrate zu ermitteln, kannst du zunächst das Maximum der Funktion  bestimmen. Prüfe, ob es Randextrema gibt.
bestimmen. Prüfe, ob es Randextrema gibt.
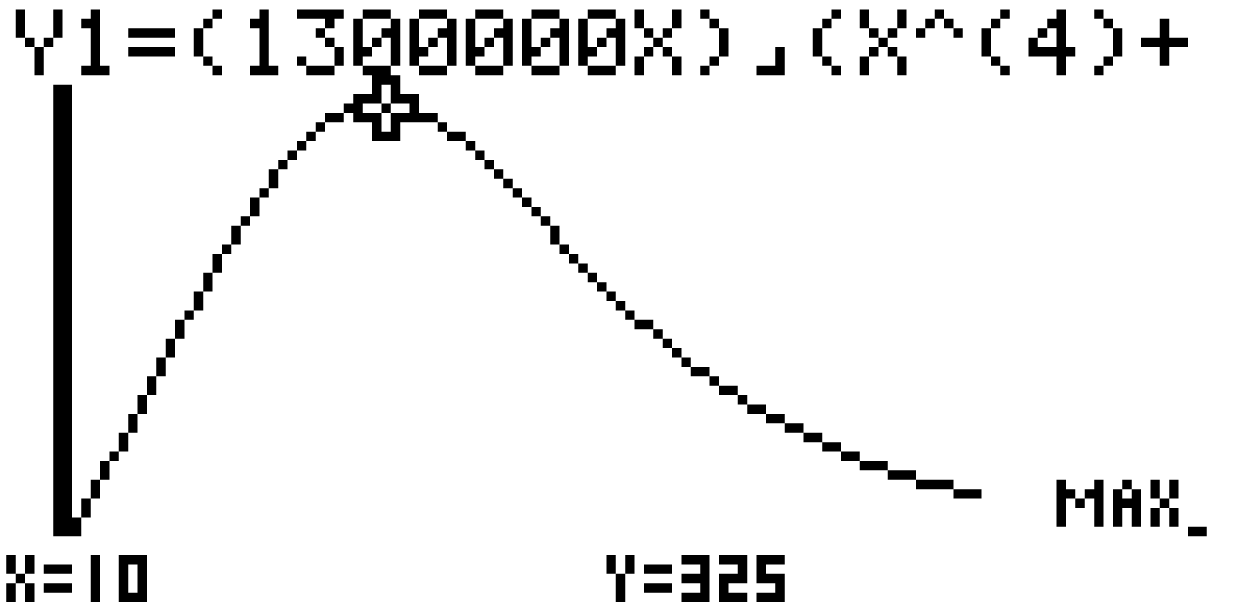 Die Koordinaten des Hochpunktes kannst du mit deinem GTR berechnen. Lasse dir dazu zunächst den Graphen der Funktion für
Die Koordinaten des Hochpunktes kannst du mit deinem GTR berechnen. Lasse dir dazu zunächst den Graphen der Funktion für  zeichnen. Das Maximum kannst du dir mit folgendem Befehl berechnen lassen:
zeichnen. Das Maximum kannst du dir mit folgendem Befehl berechnen lassen:
Anhand des Graphen siehst du, dass die Funktion kein weiteres Maximum an den Intervallgrenzen hat. Du kannst jedoch zusätzlich die Funktionswerte an den Stellen  und
und  mit dem GTR berechnen. Sind diese kleiner als der Funktionswert des Hochpunktes, so hat die Funktion
mit dem GTR berechnen. Sind diese kleiner als der Funktionswert des Hochpunktes, so hat die Funktion  keine Maxima an den Intervallgrenzen.
Die Koordinaten des Hochpunktes
keine Maxima an den Intervallgrenzen.
Die Koordinaten des Hochpunktes  lauten
lauten  . Die maximale momentane Ankunftsrate beträgt demnach 325 Fahrzeuge pro Stunde.
. Die maximale momentane Ankunftsrate beträgt demnach 325 Fahrzeuge pro Stunde.
 Anzahl der Fahrzeuge bestimmen, die in den ersten 6 Stunden ankommen
Beschreibt die Funktion
Anzahl der Fahrzeuge bestimmen, die in den ersten 6 Stunden ankommen
Beschreibt die Funktion  die momentane Ankunftsrate, so entspricht ihre Stammfunktion
die momentane Ankunftsrate, so entspricht ihre Stammfunktion  der Anzahl der ankommenden Fahrzeuge. Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden am Grenzübergang ankommen. Diese Anzahl erhältst du über folgenden Zusammenhang:
der Anzahl der ankommenden Fahrzeuge. Bestimme die Anzahl der Fahrzeuge, die in den ersten 6 Stunden am Grenzübergang ankommen. Diese Anzahl erhältst du über folgenden Zusammenhang:
 Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang. Daher ist die Konstante, die sich bei der Integration ergibt, gleich Null.
Laut Aufgabentext befinden sich zu Beginn keine Fahrzeuge vor dem Grenzübergang. Daher ist die Konstante, die sich bei der Integration ergibt, gleich Null.
Das Integral über das Intervall![\(\left[0;6\right]\)](https://mathjax.schullv.de/4f9e3c1911b7f2eaf5dc78df3b762538d9382a576594ceb6550206df6c41ba48?color=5a5a5a) kannst du mit Hilfe des GTR bestimmen.
kannst du mit Hilfe des GTR bestimmen.
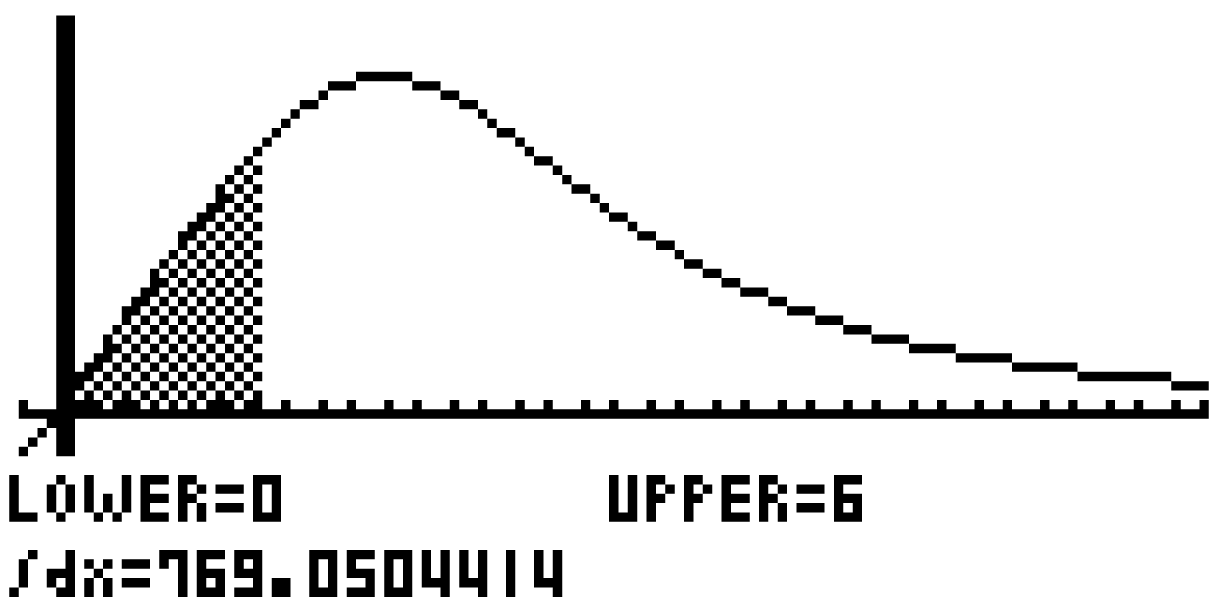 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Der GTR liefert dir, dass ungefähr 769 Fahrzeuge in den ersten 6 Stunde am Grenzübergang ankommen.
Deine Aufgabe ist es, den Graphen der Funktion
- Betrachte das Schaubild in deinem GTR, indem du den Graph-Modus auswählst.
- Lasse dir die zugehörige Wertetabelle der Funktion einblenden. Diese findest du im Graph-Modus unter TABLE :


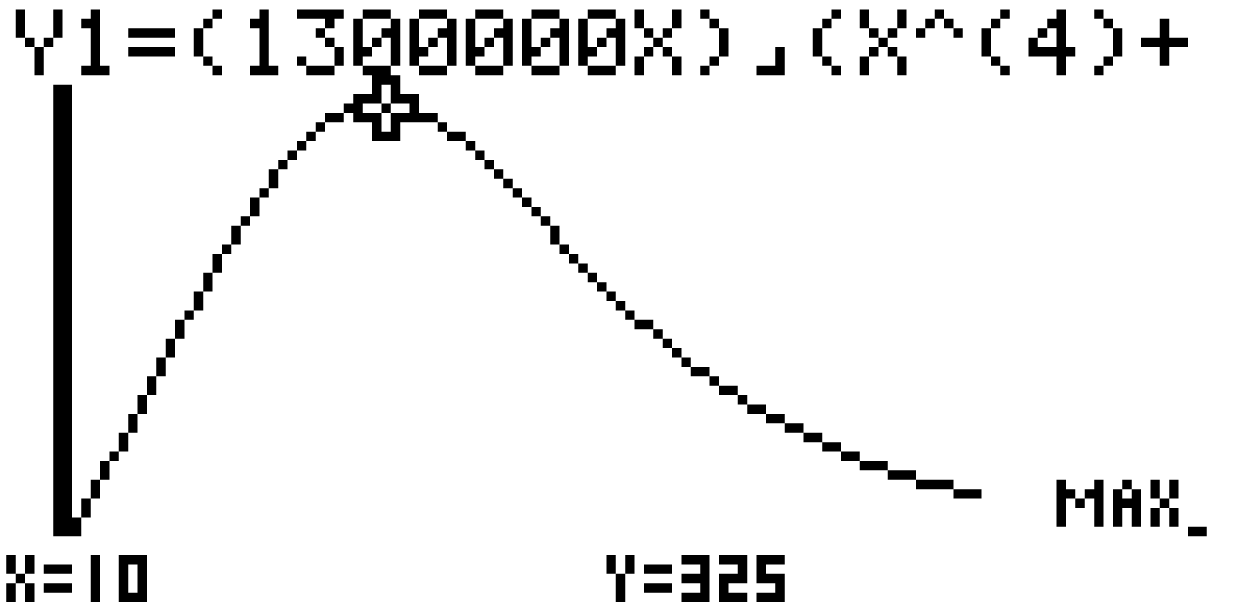
|
menu |
Das Integral über das Intervall

|
F2: G-Solve |
b)  Zeitpunkt bestimmen, an dem sich erstmals Fahrzeuge stauen
Pro Stunde können am Grenzübergang
Zeitpunkt bestimmen, an dem sich erstmals Fahrzeuge stauen
Pro Stunde können am Grenzübergang  Fahrzeuge abgefertigt werden. Aus dem Aufgabenteil zuvor weißt du jedoch, dass die maximale momentane Ankunftsrate 325 Fahrzeuge pro Stunde beträgt. Das heißt, dass zu einem gewissen Zeitpunkt mehr Fahrzeuge am Grenzübergang ankommen als abgefertigt werden können.
Fahrzeuge abgefertigt werden. Aus dem Aufgabenteil zuvor weißt du jedoch, dass die maximale momentane Ankunftsrate 325 Fahrzeuge pro Stunde beträgt. Das heißt, dass zu einem gewissen Zeitpunkt mehr Fahrzeuge am Grenzübergang ankommen als abgefertigt werden können.
Deine Aufgabe ist es, diesen Zeitpunkt zu bestimmen. Dabei kannst du wie folgt vorgehen:
zu bestimmen. Dabei kannst du wie folgt vorgehen:
 und der Geraden
und der Geraden  im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem
im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem  den Funktionswert 110 erreicht.
den Funktionswert 110 erreicht.
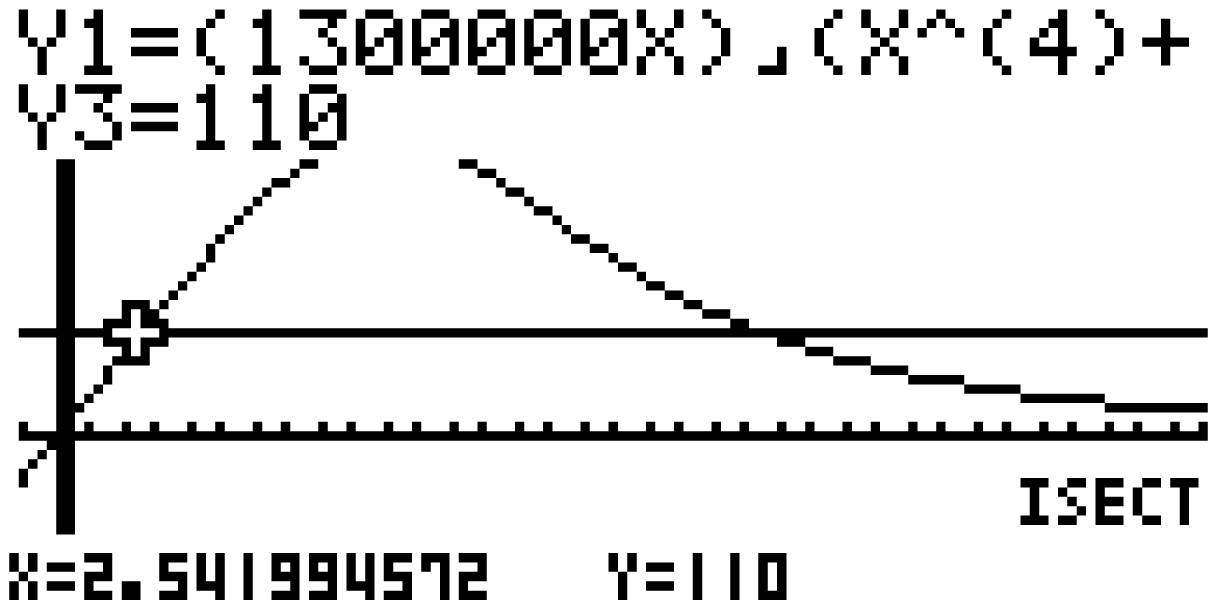 Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit EXE liefert dir zwei verschiedene Resultate:
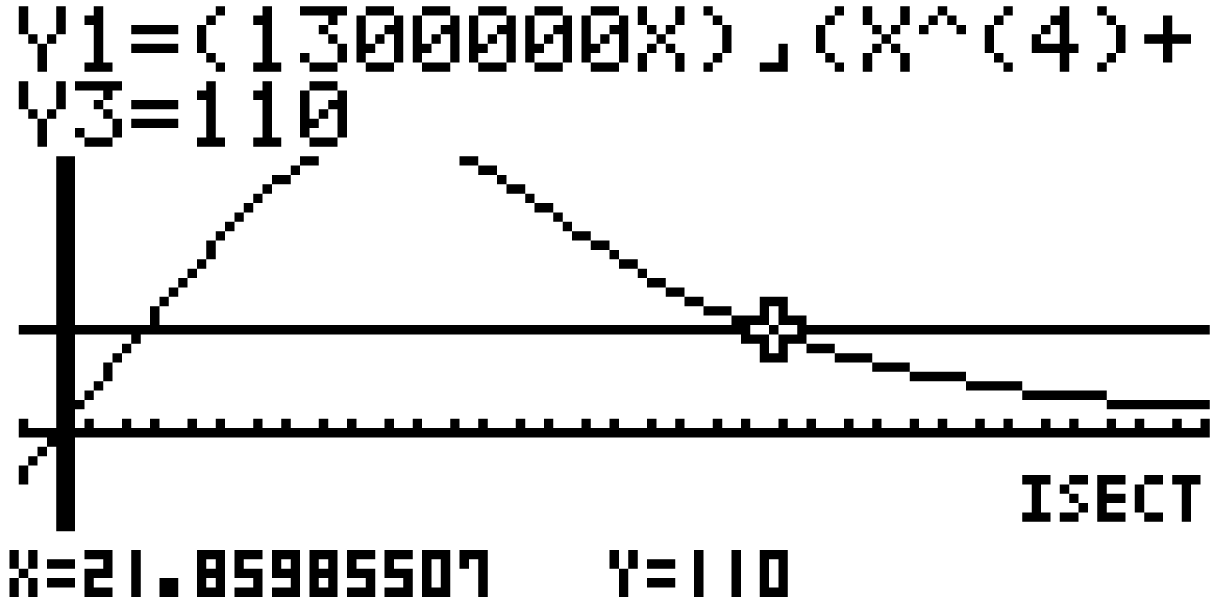 Anhand des Graphen der Funktion
Anhand des Graphen der Funktion  kannst du erkennen, dass an
kannst du erkennen, dass an  erstmalig die Anzahl von 110 pro Stunde ankommenden Fahrzeugen überschritten wird. Das liefert dir, dass der gesuchte Zeitpunkt
erstmalig die Anzahl von 110 pro Stunde ankommenden Fahrzeugen überschritten wird. Das liefert dir, dass der gesuchte Zeitpunkt  ist.
ist.
Nach 2,54 Stunden beginnen sich Fahrzeuge vor dem Grenzübergang zu stauen. Anzahl der Fahrzeuge ermitteln, die sich vor dem Übergang stauen
In der Abbildung unten siehst du den skizzierten Graphen der Funktion
Anzahl der Fahrzeuge ermitteln, die sich vor dem Übergang stauen
In der Abbildung unten siehst du den skizzierten Graphen der Funktion  und der Geraden
und der Geraden  . Zuvor hast du ermittelt, dass sich erstmalig zum Zeitpunkt
. Zuvor hast du ermittelt, dass sich erstmalig zum Zeitpunkt  Fahrzeuge vor dem Übergang stauen. Die Anzahl
Fahrzeuge vor dem Übergang stauen. Die Anzahl  der Fahrzeuge, die sich maximal vor dem Übergang anstauen, entspricht der rot markierten Fläche:
der Fahrzeuge, die sich maximal vor dem Übergang anstauen, entspricht der rot markierten Fläche:
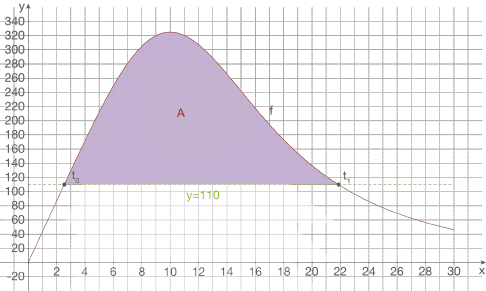 Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
 Dabei sind
Dabei sind  und
und  die Schnittstellen der Funktion
die Schnittstellen der Funktion  und der Gerdaden
und der Gerdaden  , die du zuvor bestimmt hast mit:
, die du zuvor bestimmt hast mit:
![\(\left[t_0;t_1\right]\)](https://mathjax.schullv.de/3fd6f5ac2f7bc9960f5df993e2f1f3fdcc14be1502199f30bce421974ae8d077?color=5a5a5a) gewählt, da ab dem Zeitpunkt
gewählt, da ab dem Zeitpunkt  wieder weniger Fahrzeuge ankommen, als abgefertigt werden können. Das heißt, die Anzahl
wieder weniger Fahrzeuge ankommen, als abgefertigt werden können. Das heißt, die Anzahl  nimmt ab.
nimmt ab.
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest.
Das Integral über das Intervall![\(\left[t_0;t_1\right]\)](https://mathjax.schullv.de/3fd6f5ac2f7bc9960f5df993e2f1f3fdcc14be1502199f30bce421974ae8d077?color=5a5a5a) kannst du mit Hilfe des GTR bestimmen.
kannst du mit Hilfe des GTR bestimmen.
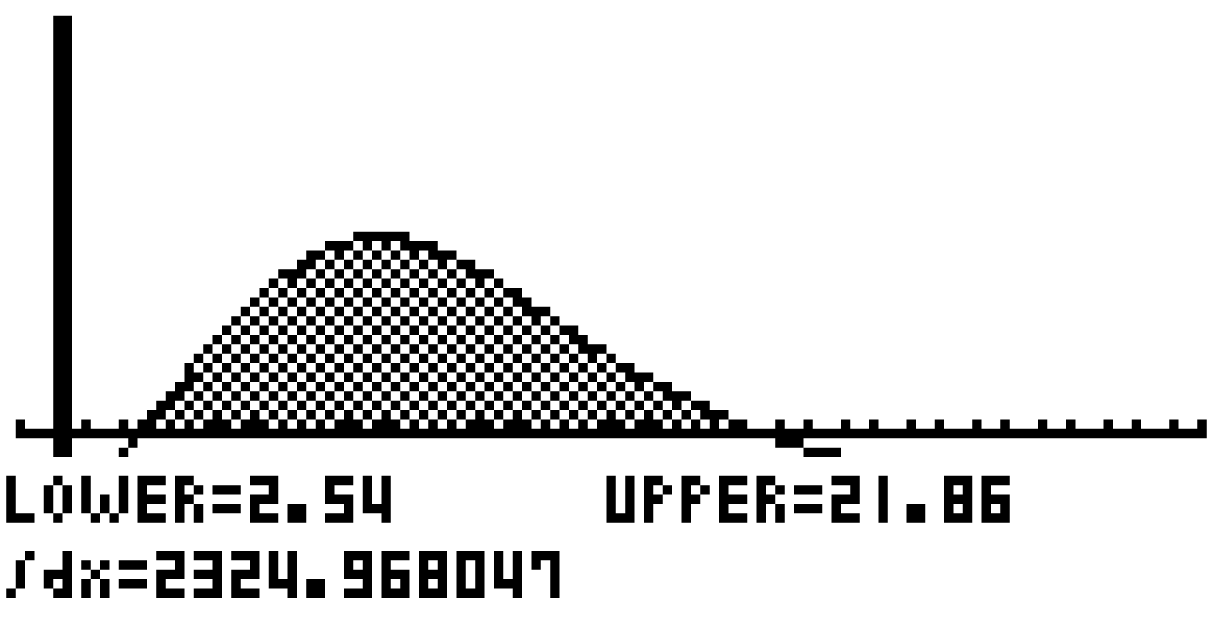 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Gib die Integrationsgrenzen und den Integranden an.
Der GTR liefert dir, dass sich maximal 2.325 Fahrzeuge am Grenzübergang anstauen.
 Anzahl bei einer Abfertigungsrate von 220 Fahrzeugen pro Stunde
12 Stunden nach Beobachtungsbeginn soll die momentane Abfertigungsate auf
Anzahl bei einer Abfertigungsrate von 220 Fahrzeugen pro Stunde
12 Stunden nach Beobachtungsbeginn soll die momentane Abfertigungsate auf  Fahrzeuge pro Stunde erhöht werden. In den Stunden davor soll die momentane Abfertigungsrate weiterhin 110 Fahrzeuge pro Stunde betragen.
Fahrzeuge pro Stunde erhöht werden. In den Stunden davor soll die momentane Abfertigungsrate weiterhin 110 Fahrzeuge pro Stunde betragen.
Berechne unter diesen Voraussetzungen die Anzahl der sich anstauenden Fahrzeuge. Die gesuchte Anzahl entspricht hier der rot markierten Fläche.
entspricht hier der rot markierten Fläche.
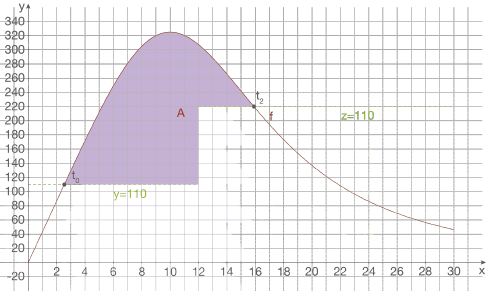 Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
Diese Fläche entspricht weiterhin gerade der folgenden Differenz:
 Dabei ist
Dabei ist  die Schnittstelle der Funktion
die Schnittstelle der Funktion  und der Geraden
und der Geraden  , die du zuvor bestimmt hast mit:
, die du zuvor bestimmt hast mit:  .
.
Dahingegen ist die Schnittstelle der Funktion
die Schnittstelle der Funktion  und der Geraden
und der Geraden  . Um die gesuchte Anzahl zu ermitteln, kannst du also wie folgt vorgehen:
. Um die gesuchte Anzahl zu ermitteln, kannst du also wie folgt vorgehen:
 bestimmen
Das kannst du mittels GTR graphisch lösen. Gib dazu den Term der Funktion
bestimmen
Das kannst du mittels GTR graphisch lösen. Gib dazu den Term der Funktion  und der Geraden
und der Geraden  im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem
im Graph-Modus an und bestimme ihre Schnittstelle. Denn diese entspricht gerade dem gesuchten Zeitpunkt, an dem  den Funktionswert 220 erreicht.
den Funktionswert 220 erreicht.
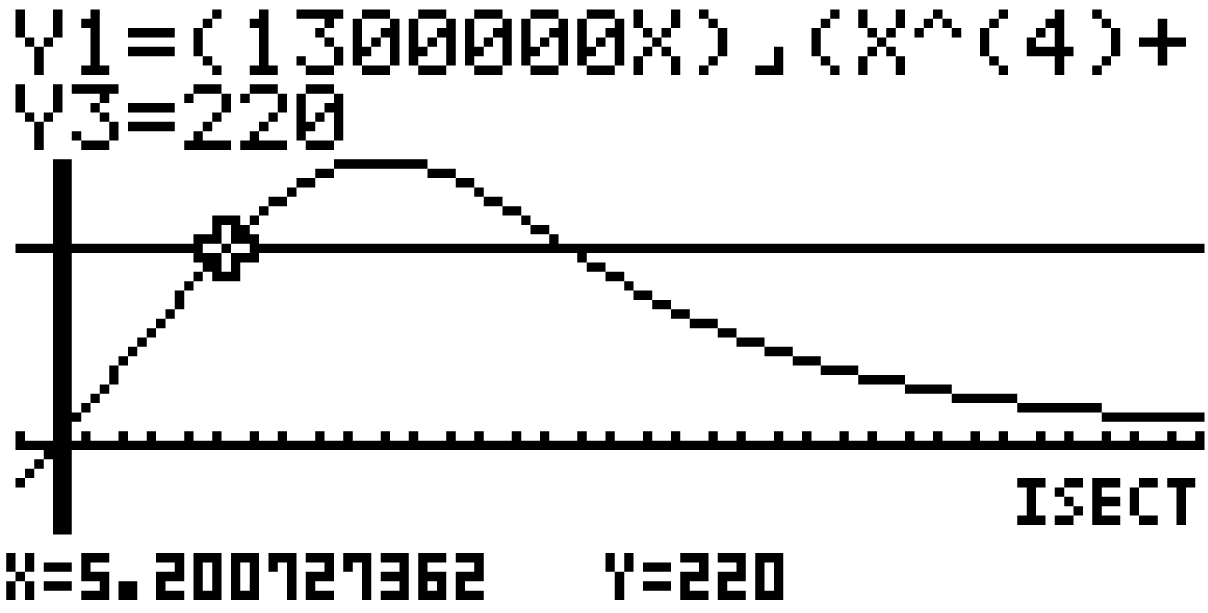 Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Um Schnittstellen von Graphen zu bestimmen, kannst du im Graph-Modus folgenden Befehl auswählen:
Bestätigen mit Enter liefert dir zwei verschiedene Resultate:
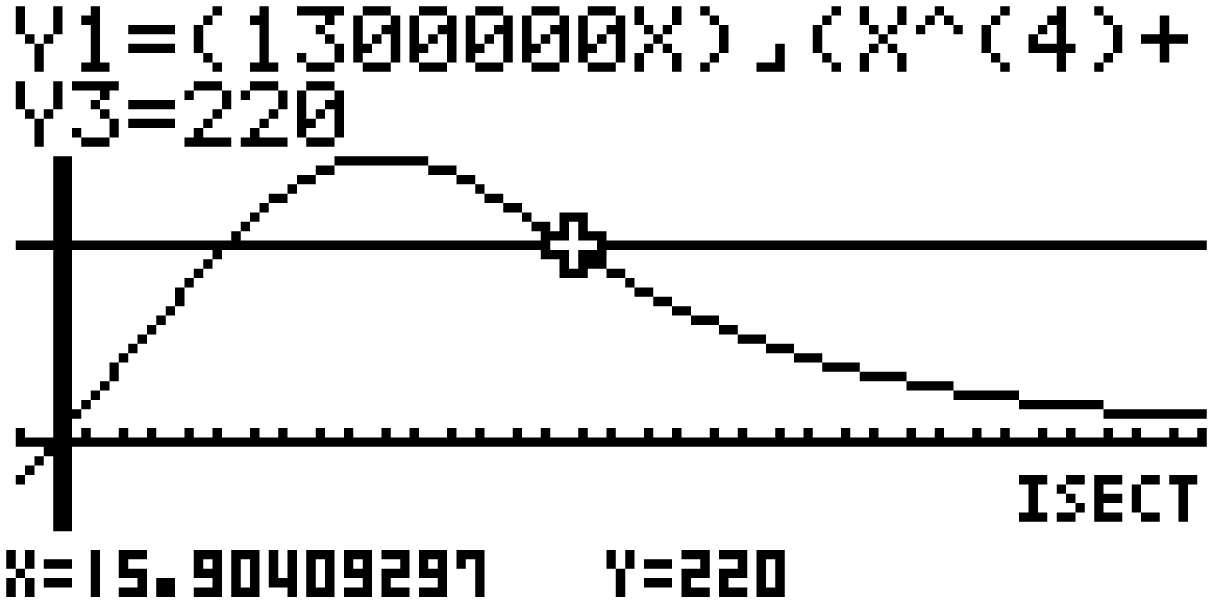 Anhand des Graphen der Funktion
Anhand des Graphen der Funktion  kannst du erkennen, dass an
kannst du erkennen, dass an  erstmalig die Anzahl von 220 pro Stunde ankommenden Fahrzeugen überschritten wird. Da aber erst nach 12 Stunden auf 220 erhöht werden soll, kannst du dieses Resultat vernachlässigen. Das liefert dir, dass der gesuchte Zeitpunkt
erstmalig die Anzahl von 220 pro Stunde ankommenden Fahrzeugen überschritten wird. Da aber erst nach 12 Stunden auf 220 erhöht werden soll, kannst du dieses Resultat vernachlässigen. Das liefert dir, dass der gesuchte Zeitpunkt  ist.
2. Schritt: Anzahl der sich anstauenden Fahrzeuge berechnen
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest. Das Integral
ist.
2. Schritt: Anzahl der sich anstauenden Fahrzeuge berechnen
Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest. Das Integral
 kannst du mit Hilfe des GTR bestimmen.
kannst du mit Hilfe des GTR bestimmen.
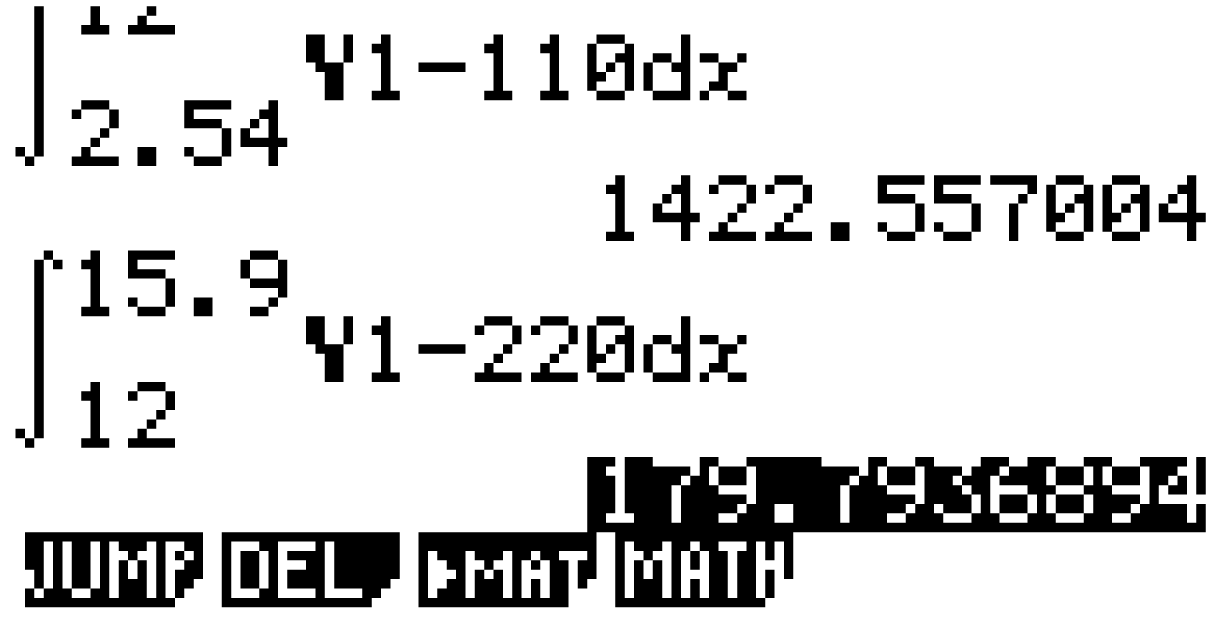 Den entsprechenden Befehl findest du unter
Den entsprechenden Befehl findest du unter
Gib die Integrationsgrenzen und den Integranden an. Diesen erhältst du über die folgende Befehlsfolge:
Wähle in diesem Menü dann die entsprechende Funktion  aus, unter welcher du den Term von
aus, unter welcher du den Term von  abgespeichert hast.
abgespeichert hast.
Der GTR liefert dir, dass sich durch die Erhöhung ab der 12. Stunde auf 220 Fahrzeuge pro Stunde maximal Fahrzeuge am Grenzübergang anstauen.
Fahrzeuge am Grenzübergang anstauen.
Deine Aufgabe ist es, diesen Zeitpunkt
- Der Zeitpunkt entspricht der Stelle von
, an der
erstmals den Funktionswert 110 erreicht. Setze also den Term der Funktion
mit 110 gleich.
- Löse nach
auf, um den gesuchten Zeitpunkt zu erhalten.

|
menu |

Nach 2,54 Stunden beginnen sich Fahrzeuge vor dem Grenzübergang zu stauen.

Berechne also die Anzahl der sich anstauenden Fahrzeuge, indem du oben angeführtes Integral berechnest.
Das Integral über das Intervall

|
F2: G-Solve |
Berechne unter diesen Voraussetzungen die Anzahl der sich anstauenden Fahrzeuge. Die gesuchte Anzahl

Dahingegen ist
- Bestimme die Schnittstelle
der Funktion
und der Geraden
.
- Berechne das Integral
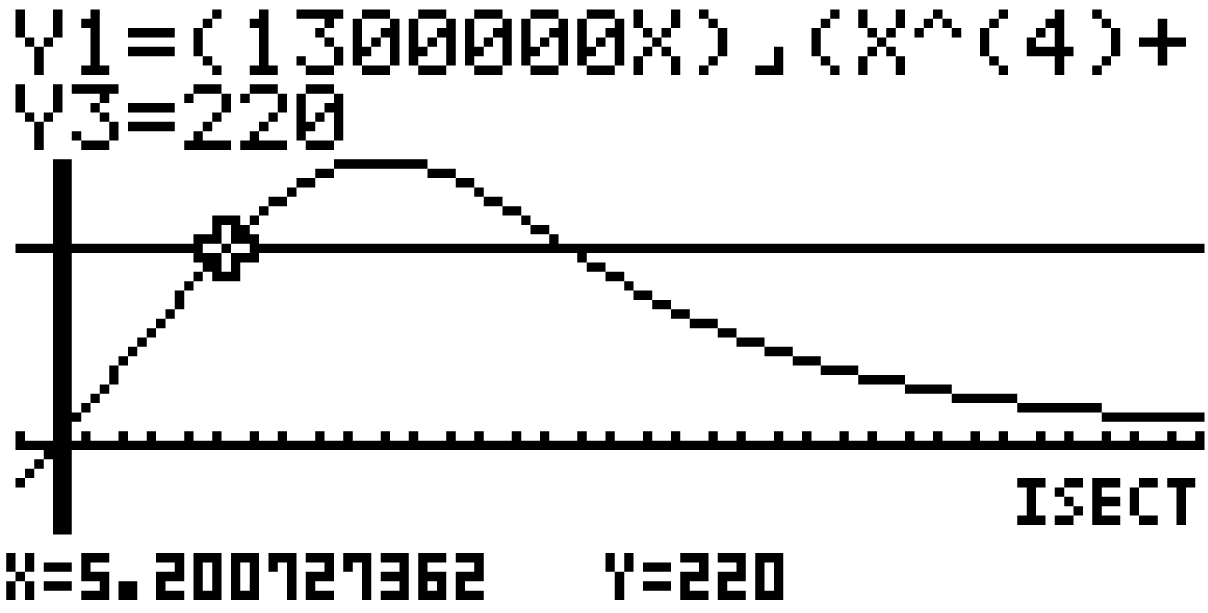
|
menu |

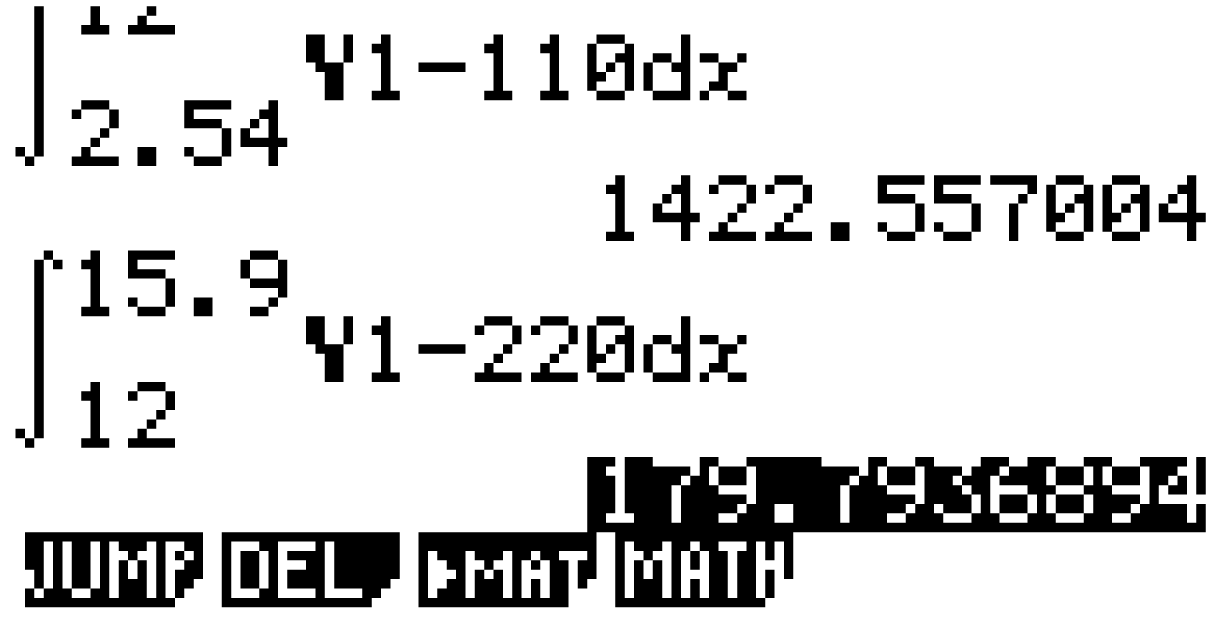
|
MATH |
|
VARS |
Der GTR liefert dir, dass sich durch die Erhöhung ab der 12. Stunde auf 220 Fahrzeuge pro Stunde maximal
Lösung A2.2
a)  Koordinaten des Extrempunktes angeben
Die Funktionenschar
Koordinaten des Extrempunktes angeben
Die Funktionenschar  mit
mit  und dem Definitionsbereich
und dem Definitionsbereich  ist durch folgenden Term definiert:
ist durch folgenden Term definiert:
 In der Aufgabenstellung wird angegeben, dass der Graph der Funktionenschar
In der Aufgabenstellung wird angegeben, dass der Graph der Funktionenschar  einen Extrempunkt besitzt. Deine Aufgabe ist es, dessen Koordinaten anzugeben. Beachte, dass diese Koordinaten vom Parameter
einen Extrempunkt besitzt. Deine Aufgabe ist es, dessen Koordinaten anzugeben. Beachte, dass diese Koordinaten vom Parameter  abhängig sein können, da es sich hierbei um eine Funktionenschar handelt.
abhängig sein können, da es sich hierbei um eine Funktionenschar handelt.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle einer Funktion
einer Funktion  müssen folgende Kriterien erfüllt werden:
müssen folgende Kriterien erfüllt werden:
 . Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von
. Hast du diese bestimmt, so kannst du die bestimmte Stelle in den Funktionsterm von  einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion
einsetzen und erhältst so den zugehörigen Funktionswert an dieser Extremstelle.
1. Schritt: Notwendige Bedingung überprüfen
Um die notwendige Bedingung einer Extremstelle der Funktion  zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion
zu überprüfen, benötigst du die erste Ableitungsfunktion der Funktion  .
.
 Für die notwendige Bedingung einer Extremstelle muss
Für die notwendige Bedingung einer Extremstelle muss  gelten. Setze den Funktionsterm der ersten Ableitung
gelten. Setze den Funktionsterm der ersten Ableitung  gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
gleich Null und ermittle alle potentielle Werte, für die diese Gleichung erfüllt wird:
 Im ersten Schritt dürfen wir durch
Im ersten Schritt dürfen wir durch  dividieren, da
dividieren, da  Voraussetzung ist.
Voraussetzung ist.
Weiterhin weißt du, dass die Sinusfunktion für den Wert Null annimmt. Da die Funktionenschar
den Wert Null annimmt. Da die Funktionenschar  aber nur im Bereich
aber nur im Bereich  definiert ist, kommt nur
definiert ist, kommt nur  als Nullstelle in Frage.
als Nullstelle in Frage.
Damit hast du eine potentielle Extremstelle an ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung
ermittelt und kannst für diese Stelle nun das hinreichende Kriterium überprüfen.
2. Schritt: Hinreichende Bedingung überprüfen
Damit eine Extremstelle vorliegt, muss weiterhin die hinreichende Bedingung  erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion
erfüllt werden. Das heißt, du benötigst zunächst die zweite Ableitung der Funktion  . Diese erhältst du, indem du den Term von
. Diese erhältst du, indem du den Term von  erneut ableitest:
erneut ableitest:
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/b2dc8306491b985c8622106e6b4dccf1a79a1c61f01d1056d1f544a2155370f6?color=5a5a5a) Überprüfe nun, ob
Überprüfe nun, ob  erfüllt wird:
erfüllt wird:
 Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist, da
Das liefert dir, dass ebenfalls die hinreichende Bedingung erfüllt ist, da  gilt. Das heißt, an
gilt. Das heißt, an  liegt eine Extremstelle vor. Wegen
liegt eine Extremstelle vor. Wegen  kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle
kannst du festhalten, dass es sich hierbei um einen Hochpunkt handelt.
3. Schritt: Koordinaten des Hochpunktes angeben
Aus den Berechnungen zuvor weißt du, dass sich an der Stelle  ein Hochpunkt befindet. Damit hast du die
ein Hochpunkt befindet. Damit hast du die  -Koordinate des Hochpunktes ermittelt. Die
-Koordinate des Hochpunktes ermittelt. Die  -Koordinate erhältst du, indem du
-Koordinate erhältst du, indem du  in den Funktionsterm von
in den Funktionsterm von  einsetzt und berechnest:
einsetzt und berechnest:
 Die Koordinaten des Extrempunktes
Die Koordinaten des Extrempunktes  lauten
lauten  .
.
Um die Koordinaten angeben zu können, musst du zunächst die notwendige und hinreichende Bedingung für Extremstellen überprüfen.
Für eine Extremstelle
- Notwendige Bedingung:
- Hinreichende Bedingung:
Weiterhin weißt du, dass die Sinusfunktion für
Damit hast du eine potentielle Extremstelle an
b)  Punkte auf der
Punkte auf der  -Achse angeben
-Achse angeben
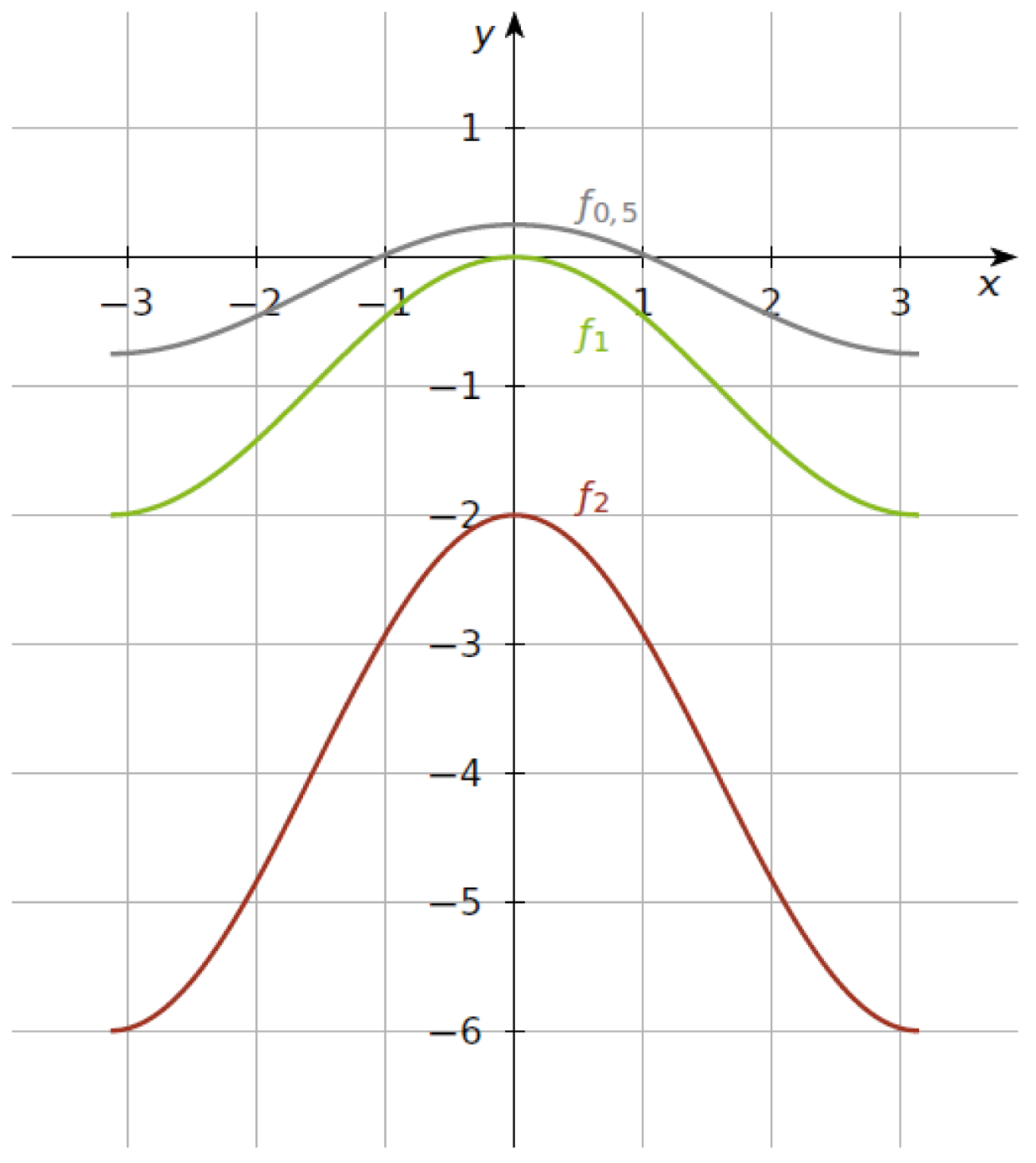 Im Schaubild kannst du erkennen, dass die Graphen der Funktionen
Im Schaubild kannst du erkennen, dass die Graphen der Funktionen  ,
,  und
und  der Funktionenschar
der Funktionenschar  jeweils einen Punkt auf der
jeweils einen Punkt auf der  -Achse schneiden. Gib die Punkte an, durch welche kein Graph der Funktionenschar
-Achse schneiden. Gib die Punkte an, durch welche kein Graph der Funktionenschar  verläuft.
verläuft.
Dabei kannst du folgende Eigenschaften verwenden: mit dem Term
mit dem Term  und der Bedingung
und der Bedingung  .
.
Diese Hilfsfunktion gibt die -Koordinate des Schnittpunktes
-Koordinate des Schnittpunktes  mit der
mit der  -Achse in Abhängigkeit von
-Achse in Abhängigkeit von  an.
an.
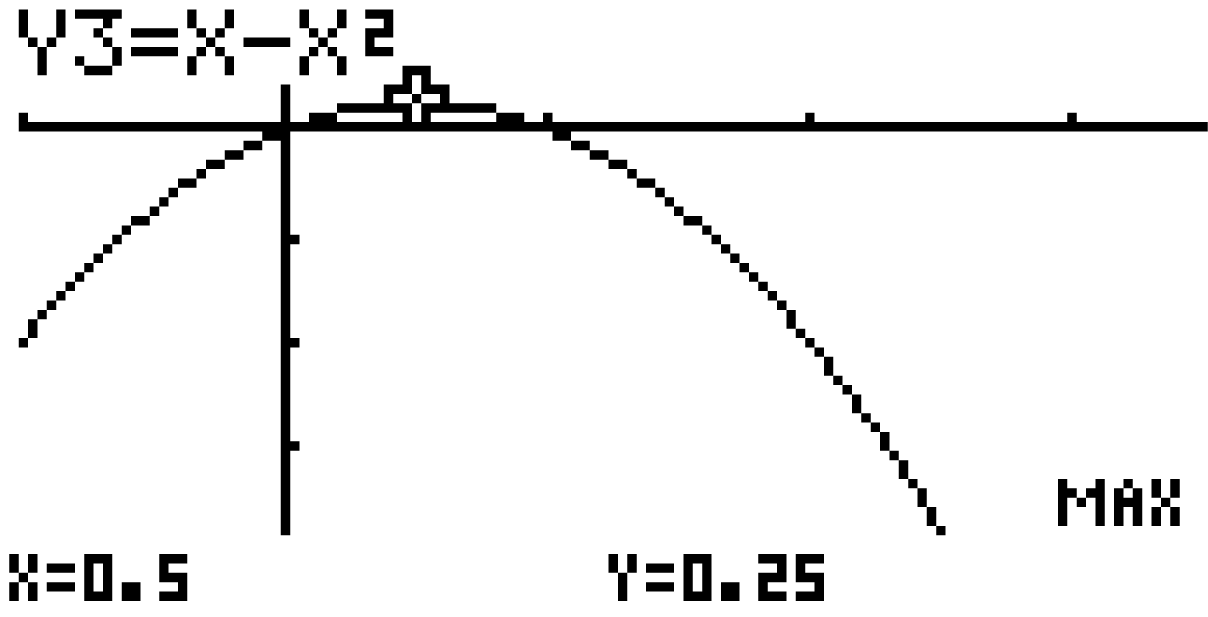 Lässt du die Hilfsfunktion in deinem GTR zeichnen, so kannst du erkennen, dass die Funktion
Lässt du die Hilfsfunktion in deinem GTR zeichnen, so kannst du erkennen, dass die Funktion  nach unten nicht beschränkt ist.
nach unten nicht beschränkt ist.
Ihr Maximum kannst du ermitteln, indem du
auswählst.
Der GTR liefert dir, dass sich das Maximum an mit
mit  befindet. Das heißt, der Extrempunkt bzw. Schnittpunkt mit der
befindet. Das heißt, der Extrempunkt bzw. Schnittpunkt mit der  -Achse kann maximal die
-Achse kann maximal die  -Koordinate
-Koordinate  besitzen.
besitzen.
Du kannst also festhalten, dass der Graph der Funktionenschar die Punkte
die Punkte  auf der
auf der  -Achse nicht berührt, für die
-Achse nicht berührt, für die  gilt.
gilt.

Dabei kannst du folgende Eigenschaften verwenden:
- Laut Aufgabentext muss
gelten.
- Der Extrempunkt besitzt die Koordinaten
und stellt damit den Schnittpunkt mit der
-Achse dar.
Diese Hilfsfunktion gibt die

Ihr Maximum kannst du ermitteln, indem du
|
menu |
Der GTR liefert dir, dass sich das Maximum an
Du kannst also festhalten, dass der Graph der Funktionenschar