Wahlteil A1

Aufgabe A1.1

Das Gelände eines Abenteuerspielplatzes besteht aus einer Hochfläche, an die sich ein Hang mit einer Senke anschließt. Die Profillinie des Geländes wird für $-3\leq x \leq0$ durch die Gerade mit der Gleichung $y=5$ und für $0\leq x \leq 11$ durch den Graphen der Funktion f mit $f(x)=0,0008 x^4 -0,12x^2+5$ beschrieben. Die Abbildung zeigt diese Profillinie (1 LE entspricht 1 m).

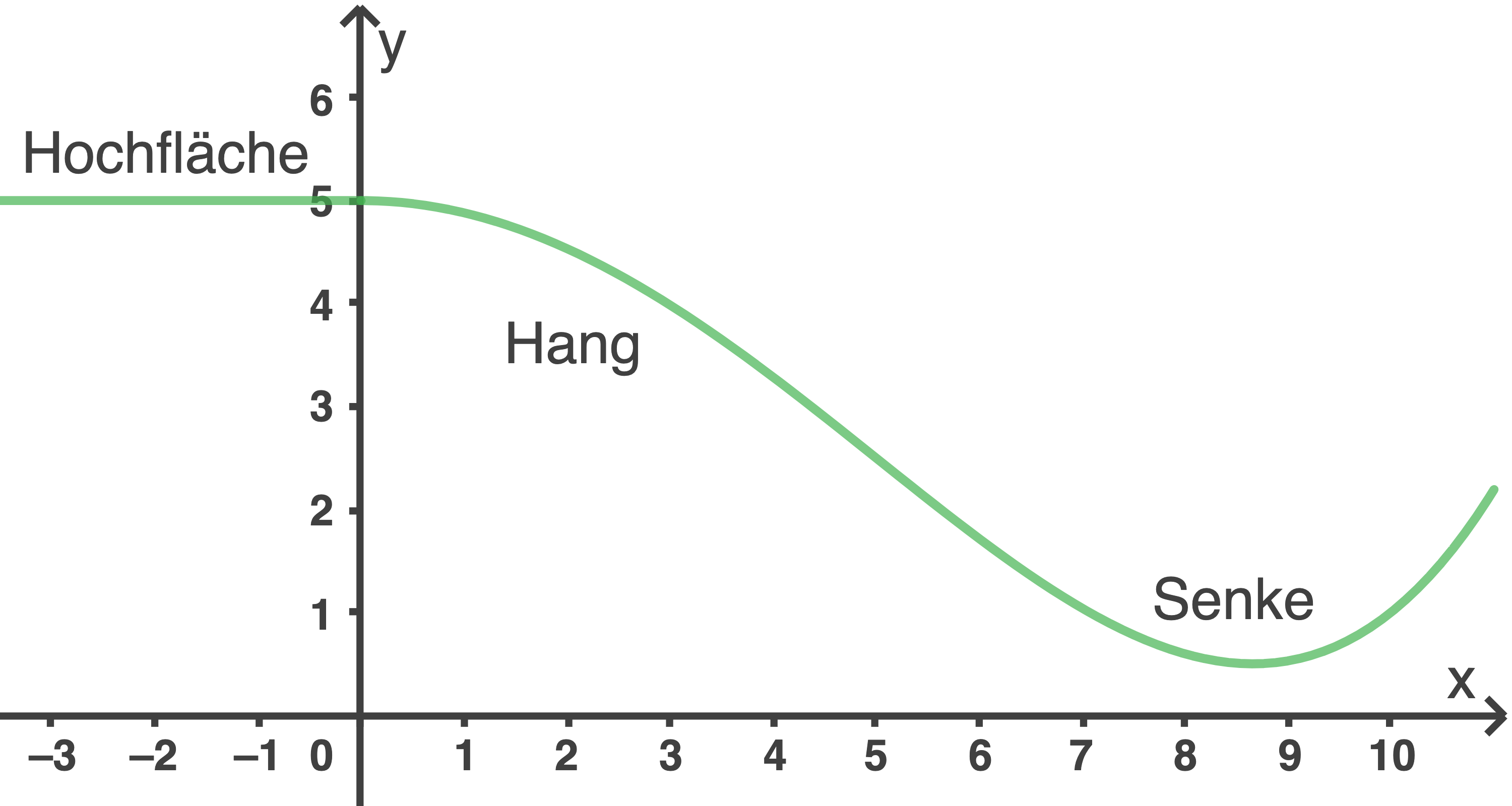
Grafik einer Kurve mit Hochfläche, Hang und Senke, dargestellt in einem Koordinatensystem.

Berechne die Koordinaten des tiefsten Punkts der Profillinie.

(2 VP)

Weise rechnerisch nach, dass der Hang zwischen Hochfläche und Senke an der Stelle $x=5$ am steilsten abfällt und dort ein Gefälle von 80 % hat.

(2 VP)

Zeige, dass die Profillinie beim Übergang von der Hochfläche zum Hang knickfrei ist.

(1 VP)

(Teilergebnis: Der tiefste Punkt hat die $y$ -Koordinate 0,5.)

Zwischen zwei Befestigungspunkten, die im Modell durch $P(5 \mid f(5))$ und $Q(10\mid f(10))$ dargestellt werden, wird ein Seil straff gespannt.
Berechne die Länge des Seils.

(1,5 VP)

Beschreibe ein Verfahren, mit dem die maximale vertikale Höhe des Seils über dem Gelände berechnet werden kann.

(2 VP)

Auf der Hochfläche, einen Meter vom Übergang zum Hang entfernt, steht ein vertikaler Lichtmast, von dem aus das gesamte Gelände ausgeleutet werden kann.
Berechne die Mindestlänge dieses Lichtmasts.

(2,5 VP)

Bei einem Umbau soll die Senke auf $5\,\text{ m}$ Länge so mit Sand aufgefüllt werden, dass eine horizontale rechteckige Fläche entsteht, die $0,5 \, \text{m}$ oberhalb des tiefsten Punkts der Senke liegt.
Berechne das Volumen des dafür benötigten Sandes.

Grafik eines gebogenen Objekts mit einer Markierung von 5 m.

(3,5 VP)

Aufgabe A1.2

Abgebildet sind die Graphen $G_u$ und $G_v$ zweier Funktionen $u$ und $v.$
Die Funktion $f$ ist gegeben durch $f(x)=v(u(x)).$
Bestimme $f(-1).$

(1 VP)

Ermittle die Anzahl der Nullstellen von $f$ im abgebildeten Bereich.

(1,5 VP)

Grafik mit zwei Kurven G_u und G_v im Koordinatensystem, das die Achsen x und y zeigt.

Aufgabe A 1.3

Die Funktion $w$ ist auf $\mathbb{R}$ definiert und zweimal differenzierbar.
Für die Funktion $g$ gilt: $g(x)=\mathrm e^{w(x)}-2.$

Zeige: Wenn $x_0$ eine Wendestelle von $w$ und von $g$ ist, dann hat der Graph von $w$ bei $x_0$ eine waagrechte Tangente.

(3 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung A1.1

Tiefster Punkt
Der tiefste Punkt ist der Tiefpunkt.
Mit dem notwendigen Kriterium für Extremstellen ergibt sich:

$\(\begin{array}[t]{rll} f$

Mit dem Satz vom Nullprodukt folgt $x_1=0$ und

$\begin{array}[t]{rll} 0&=& 0,0032 x^2-0,24 &\quad \scriptsize \mid\; +0,24 \mid\;:0,0032 \\[5pt] 75&=& x^2&\quad \scriptsize \\[5pt] \end{array}$

Daraus ergibt sich $x_2 =\sqrt{75}$ und $x_3= -\sqrt{75}$ wobei $x_3$ außerhalb des betrachteten Bereichs liegt.

Mit dem hinreichenden Kriterium für Extremstellen folgt:

$\(\begin{array}[t]{rll} f$

Da $\(f$ ist besitzt der Graph von $f$ hier einen Tiefpunkt.

$f(\sqrt{75})=0,5$

Die Koordinaten des tiefsten Punkts der Profillinie lauten $T( \sqrt{75} \mid 0,5).$

Am steilsten fallende Stelle
Die am steilsten abfallende Stelle ist die Wendestelle bzw. eine Minimalstelle von $\(f$
Mit dem notwendigen Kriterium für Wendestellen ergibt sich:

$\(\begin{array}[t]{rll} 0 &=& f$

$x =-5$ liegt allerdings außerhalb des betrachteten Bereichs.
Mit dem hinreichenden Kriterium für Wendestellen folgt für $x=5:$

$\(\begin{array}[t]{rll} f$

Damit besitzt $f$ an der Stelle $x=5$ eine Wendestelle, sowie $\(f$ ein Minimum. Daher ist dies die Stelle, an der der Hang am steilsten abfällt.

Für die Steigung an dieser Stelle gilt:

$\(f$

Das Gefälle beträgt an der steilsten Stelle also 80 %.

Knickfreier Übergang
Es gilt $f(0)=5$ und $\(f$ sodass Hochfläche und Hang auf gleicher Höhe und mit gleicher Steigung ineinander übergehen und der Übergang somit knickfrei ist.

Seillänge
$f(5)$ $= 0,0008 \cdot 5^4 -0,12\cdot 5^2+5$ $= 2,5$

$f(10)$ $= 0,0008 \cdot 10^4 -0,12\cdot 10^2+5$ $= 1$

Die Länge des Seils ergibt sich damit zu:

$\sqrt{(10-5)^2+(f(10)-f(5))^2}\,$ $=\sqrt{5^2+(1-2,5)^2}\,$ $\approx5,22 \,(\text{m})$

Verfahren beschreiben
Es wird eine Gerade durch die Punkte $P$ und $Q$ gelegt, die durch eine Funktion $s$ beschrieben wird und den Verlauf des Seils beschreibt. Dann wird $d(x)=s(x)-f(x)$ als Funktion bestimmt, die den vertikalen Abstand zwischen dem Seil und dem Gelände beschreibt. Das Maximum von $d$ im Intervall $[5,10]$ entspricht der maximalen Höhe.

Mindestlänge Lichtmast
Es muss die Tangente im Wendepunkt an den Graphen von f bestimmt werden und $x=-1$ eingesetzt werden.

$\(\begin{array}[t]{rll} t: \, y&=& f$

$y=-0,8 \cdot (-1-5)+2,5= 7,3$

Der Mast ist folglich mindestens $7,3-5=2,3$ Meter lang.

Volumen berechnen
Da der tiefste Punkt der Senke auf einer Höhe von $0,5\,\text{m}$ liegt, kann die rechteckige Fläche im Querschnitt durch die Gerade zu $y= 0,5 +0,5 =1$ beschrieben werden.
Die Größe der Querschnittsfläche des aufgeüllten Sandes lässt sich mit Hilfe des Flächeninhalts berechnen, der vom Graphen von $f$ und der Geraden $y=1$ eingeschlossen wird.
Für die Schnittstellen dieser Graphen ergibt sich:

$\begin{array}[t]{rll} f(x) &=& 1 \\[5pt] 0,0008 x^4 -0,12x^2 +5&=& 1&\quad \scriptsize \mid\;-1 \\[5pt] 0,0008 x^4 -0,12x^2 +4&=& 0&\quad \scriptsize \\[5pt] \end{array}$

Mit der Substitution von $z=x^2$ ergibt sich folgende Gleichung, die mit der $pq$ -Formel gelöst werden kann:

Vollständigen Rechenweg anzeigen

$\begin{array}[t]{rll} 0 &=& 0,0008 z^2 -0,12z +4 \\[5pt] && ... \\[5pt] z_1 &=& 50 \\[5pt] z_2 &=& 100 \end{array}$

Durch Resubstitution folgt:

$x_1= \sqrt{50}\approx 7,07,$ $x_2=- \sqrt{50}\approx -7,07,$ $x_3= \sqrt{100}= 10,$ $x_4= -\sqrt{100}=-10$

Im Intervall liegen nur die Stellen $x_1\approx 7,07$ und $x_3=10.$

$\displaystyle\int_{7,07}^{10}(0,0008 x^4 -0,12x^2 +4)\;\mathrm dx$ $= \left[ 0,00016 x^5 - 0,04x^3 + 4x\right]_{7,07}^{10}$ $\approx -0,97$

$A= \mid -0,97 \mid = 0,97\,[\text{m}^2]$

Das Volumen des Sandes beträgt $V= 0,97 \,\text{m}^2\cdot 5\text{m} \approx 4,85\,\text{m}^3.$

Lösung A1.2

Wert bestimmen
An der passenden Stelle am Graphen kann der entsprechende Wert abgelesen werden.

$\begin{array}[t]{rll} f(x)&=& v(u(x))&\quad \scriptsize \\[5pt] f(-1) &=& v(u(-1))&\quad \scriptsize \\[5pt] &=& v(1,5)&\quad \scriptsize \\[5pt] &=&2,5 &\quad \scriptsize \\[5pt] \end{array}$

Anzahl der Nullstellen von f(x)
Anhand des Verlaufes des Graphens können die passenden Stellen abgelesen werden.

$\begin{array}[t]{rll} f(x)&=& 0\\[5pt] v(u(x))&=& 0 \\[5pt] \end{array}$

Aus der Abbildung lässt sich ablesen, dass $v(x) =0$ für genau einen Wert, nämlich für $x\approx0,6$ gilt.
Es muss also $u(x)=0,6$ sein, damit $f(x)=0$ gilt.
Am Verlauf des Graphen ist ersichtlich, dass es zwei $x$ -Werte gibt, die $u(x)=0,6$ erfüllen. Also besitzt $f$ zwei Nullstellen im abgebildeten Bereich.

Lösung A 1.3

Für die Ableitungsfunktionen von $g$ gilt:

$\(\begin{array}[t]{rll} g$

Wenn $x_0$ eine Wendestelle von $g$ und von $w$ ist, dann gilt:

$\(w$ und

Vollständigen Rechenweg anzeigen

$\( (w$

Da $\mathrm{e}^{w(x_0)} \neq 0$ gilt, folgt mit dem Satz vom Nullprodukt $\((w$ und daher $\(w$
Also hat der Graph von $w$ bei $x_0$ eine waagrechte Tangente.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?