Wahlteil A2

Aufgabe A2.1

In einem Skigebiet beträgt die Schneehöhe um 10.00 Uhr an einer Messstelle $150\,\text{cm}.$ Die momentane Änderungsrate dieser Schneehöhe wird beschrieben durch die Funktion $s$ mit

$s(t) = 16\mathrm e^{-0,5t} - 14\mathrm e^{-t} -2;\;$ $0 \leq t \leq 12$

( $t$ in Stunden nach 10.00 Uhr, $s(t)$ in Zentimeter pro Stunde).

Bestimme die maximale momentane Änderungsrate der Schneehöhe.
Ermittle den Zeitraum, in dem die momentane Änderungsrate der Schneehöhe größer als $2\,\text{cm}$ pro Stunde ist.
Wie hoch liegt der Schnee um 12.00 Uhr?

(4 VP)

Bestimme einen integralfreien Funktionsterm, der die Schneehöhe zum Zeitpunkt $t$ beschreibt.
Zu welchen Uhrzeiten beträgt die Schneehöhe $153\,\text{cm}$ ?

(3 VP)

Um 12.30 Uhr werden nun Schneekanonen in Betrieb genommen. Sie liefern konstant so viel Schnee, dass sich die momentane Änderungsrate der Schneehöhe an der Messstelle um $1\,\text{cm}$ pro Stunde erhöht.
Um wie viele Stunden verlängert sich durch diese Maßnahme der Zeitraum, in dem die Schneehöhe zunimmt?
Wie viele Zentimeter Schnee pro Stunde müssten die Schneekanonen ab 12.30 Uhr liefern, damit um 18.00 Uhr die Schneehöhe $160\,\text{cm}$ betragen würde?

(4 VP)

Aufgabe A2.2

Für jedes $a \gt 0$ ist eine Funktion $g_a$ gegeben durch

$g_a(x) = a \cdot \cos(a \cdot x);\;$ $-\dfrac{\pi}{2a} \leq x \leq \dfrac{\pi}{2a}.$

Der Graph von $g_a$ schneidet die $y$ -Achse in einem Punkt. Die Strecke von diesem Punkt zum Ursprung ist die Diagonale einer Raute. Die beiden weiteren Eckpunkte der Raute liegen auf dem Graphen von $g_a.$

Bestimme für $a = 3$ die Längen der beiden Diagonalen dieser Raute.

(2 VP)

Bestimme den Wert von $a,$ für den die Raute ein Quadrat ist.

(2 VP)

Aufgabe A 2.1

$\blacktriangleright$ Extrempunkt bestimmen

Du hast die Funktion $s(t) = 16 \cdot \mathrm e^{-0,5t} - 14 \cdot \mathrm e^{-t} - 2$ gegeben.

Sie wird benutzt, um die Änderungsrate einer Schneehöhe in Abhängigkeit von der Zeit im Intervall $[0,12]$ zu beschreiben. Dabei wird $t$ in Stunden nach $10 \, \text{Uhr}$ gemessen und die Schneehöhe in Zentimetern. Du sollst jetzt die maximale Änderungsrate bestimmen, also das Maximum der Funktion $s$ . Dies kannst du mit deinem GTR tun.

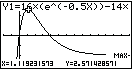
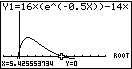
Lass dir dazu den Graphen anzeigen. Den Befehl für die Bestimmung von Hochpunkten findest du unter:

2ND $\to$ TRACE (CALC) $\to$ 4: maximum

Du erhältst als gerundete Werte die folgenden Koordinaten:

$\quad \text{H} \, (1,12 \mid 2,57)$

Grafik eines Taschenrechners mit einer Funktion und deren Maximum auf einem Koordinatensystem.

Abb. 1: Maximum von $s$

Nun musst du noch ausschließen, dass der Graph auf dem Rand seines Definitionsbereichs ein Maximum annimmt.

Das erkennst du, indem du den Graphen im Intervall [0,12] plottest oder indem du die Funktionswerte $s(0)$ und $s(12)$ berechnest und mit $2,57$ vergleichst. Auf diese Weise kannst du sehen, dass der Graph sein Maximum wirklich bei $\text{H}$ erreicht.

Du erkennst so, dass die maximale momentane Änderungsrate der Schneehöhe ungefähr $2,6 \, \dfrac{\text{cm}}{\text{h}}$ beträgt.

$\blacktriangleright$ Intervall mit nach unten beschränktem Wachstum berechnen

Gesucht ist der Zeitraum, in dem die Änderungsrate größer als $2$ ist, also das Intervall, in welchem $s(t) \gt 2$ gilt. Dies ist der Bereich zwischen den Schnittpunkten des Graphen von $s$ mit der konstanten Gerade $y =2$ .

Lass dir dazu die Funktion $s$ mit der konstanten Funktion $y = 2$ anzeigen und bestimme ihre Schnittpunkte.

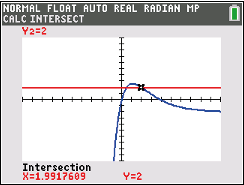
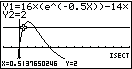
Schnittpunkte bestimmst du mit:

2ND $\to$ TRACE (CALC) $\to$ 5: intersect

Du erhältst folgende Koordinaten:

$P_1 \, (1,99 \mid 2)$ $\quad P_2 \, (0,51 \mid 2)$

Graph eines mathematischen Problems mit zwei Funktionen und ihrem Schnittpunkt.

Abb. 2: Erster Schnittpunkt von $s$ und $y$

Das Intervall, in dem $s$ größer ist als die Konstante $2$ , wird von den Schnittpunkten begrenzt. Jetzt ist nur noch wichtig, die $t$ - Werte in Stunden umzurechnen.

Also ist die momentane Änderungsrate im Intervall zwischen ca $10: 30 \,\text{Uhr}$ und $12 \, \text{Uhr}$ größer als $2 \, \dfrac{\text{cm}}{\text{h}}$ .

$\blacktriangleright$ Schneehöhe bestimmen

Im dritten Aufgabenteil ist gefragt, wie hoch der Schnee um $12 \, \text{Uhr}$ liegt. Dazu benutzt du, dass die Schneehöhe $S$ nach der Zeit abgeleitet gerade die momentane Änderungsrate der Schneehöhe $s$ ist.

$S‘ = s$

Wenn du $s$ also integrierst, erhältst du die Schneehöhe, die in einem bestimmten Intervall dazugekommen ist. Diese Aufgabe kannst du jetzt mit deinem GTR lösen. Berechne dafür zuerst die Schneemenge, die im Intervall $[0,2]$ dazukommt.

$\displaystyle\int_{0}^{2}s(t) \, \mathrm dt$

$\blacktriangleright$ Integralfreien Funktionsterm bestimmen

Gesucht ist ein integralfreier Funktionsterm für die Schneehöhe zum Zeitpunkt $t$ . Da $s$ die momentane Änderungsrate beschreibt, benötigst du also eine Stammfunktion $S$ von $s$ . Die gesuchte Funktion ist gerade die Stammfunktion $S$ von $s$ , für die $S(t)=150$ gilt, da die Schneehöhe zu Beginn der Messung $150\,\text{cm}$ beträgt.

Bestimme also zunächst die allgemeinen Stammfunktionen von $s$ :

$\begin{array}[t]{rll} s(t)&=& 16 \cdot \mathrm e^{-0,5t} - 14 \cdot \mathrm e^{-t} - 2 \\[10pt] S_c(t)&=& 16\cdot \dfrac{1}{-0,5} \cdot \mathrm e^{-0,5t} -14\cdot (-1)\cdot \mathrm e^{-t} -2t + c \\[5pt] &=&-32 \mathrm e^{-0,5t} + 14 \mathrm e^{-t} -2t + c \\[5pt] \end{array}$

$c$ muss nun so gewählt werden, dass $S_c(t) =150$ ist:

$\begin{array}[t]{rll} S_c(0)&=& 150 \\[5pt] -32 \mathrm e^{-0,5\cdot 0} + 14 \mathrm e^{-0} -2\cdot 0 + c&=& 150 \\[5pt] -32 +14 +c&=& 150 \\[5pt] -18 +c&=& 150 &\quad \scriptsize \mid\; +18 \\[5pt] c&=& 168 \end{array}$

Die Funktion $S(t) = -32 \mathrm e^{-0,5t} + 14 \mathrm e^{-t} -2t + 168$ beschreibt also die Schneehöhe zum Zeitpunkt $t$ .

$\blacktriangleright$ Uhrzeiten mit einer Schneehöhe von $\boldsymbol{153\,\text{cm}}$ bestimmen

Du hast bereits eine Funktion $S$ bestimmt, die die Schneehöhe zum Zeitpunkt $t$ beschreibt. Nun sollst du die Zeitpunkte bestimmen, zu denen die Schneehöhe $153\,\text{cm}$ beträgt. Setze also $S(t) = 153$ und löse nach $t$ auf.

Dafür kannst du deinen Taschenrechner verwenden, indem du wie zuvor den Schnittpunkt des Graphen von $S$ mit der Gerade zu $y = 153$ bestimmst. Du erhältst dann folgende Lösung:

$t_1 \approx -0,80$ $\quad$ $t_2 \approx 1,50$ $\quad$ $t_3 \approx 7,03$

Da die Messung bei $t=0$ startet, fällt $t_1$ weg. Der Schnee ist also um ca. $11.30$ Uhr und $17$ Uhr $153\,\text{cm}$ hoch.

$\blacktriangleright$ Zusätzliche Schneezunahme mit einer Schneekanone berechnen

Um $12:30 \, \text{Uhr}$ werden zusätzlich Schneekanonen eingeschaltet, die die ursprüngliche Änderungsrate um $1 \, \dfrac{\text{cm}}{\text{h}}$ erhöhen. Das heißt, dass zum Funktionsterm von $s$ eine $1$ addiert wird.

$F(t) = s(t) + 1 = 16 \mathrm e^{-0,5t} -14e^{-t} - 1$

Gefragt ist nun, um wie viele Stunden diese Maßnahme den Zeitraum verlängert, in dem die Schneehöhe zunimmt.

Dazu vergleichst du die geänderte Funktion $F$ mit deiner Ursprungsfunktion $s$ . Plotte sie mit deinem GTR. Dort, wo die Funktionen $F$ und $s$ größer als Null sind, nimmt die Schneehöhe zu. Um herauszufinden, wann die Schneehöhe abnimmt, benötigst du also die Nullstellen. Du suchst also die Nullstellen der Funktionen $s$ und $F$ mit einem Vorzeichenwechsel von $+$ nach $-$

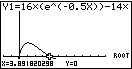
Den Befehl für die Bestimmung von Nullstellen findest du unter:

2ND $\to$ TRACE (CALC) $\to$ 2: zerp

Graph einer mathematischen Funktion auf einem Taschenrechner-Display mit Achsen und einer gekrümmten Linie.

Abb. 4: Nullstelle von $s$

Graph einer mathematischen Funktion auf einem Taschenrechner-Bildschirm mit Achsen und Nullstelle.

Abb. 5: Nullstelle von $F$

Diese Nullstellen ziehst du voneinander ab, also $5,43 - 3,88 = 1,65$ . Also verlängert sich der Zeitraum, in dem die Schneehöhe zunimmt, um ca $1,5$ Stunden.

$\blacktriangleright$ Geforderten Schneezuwachs berechnen

Hier ist gefragt, wie viele Zentimeter pro Stunde die Schneekanone ab $12:30 \, \text {Uhr}$ liefern müsste, damit um $18 \, \text {Uhr}$ die Schneehöhe $160 \, \text {cm}$ beträgt. Dazu berechnest du zunächst wie hoch der Schnee ohne Schneekanonen um $18 \, \text {Uhr}$ liegen würde.

$S(8)= 151,42$

Das bedeutet, dass zu der geforderten Höhe $160 \, \text {cm} - 151,42\, \text {cm} = 8,58 \, \text{cm}$ Schnee fehlen. Diese Menge muss von $12:30 \, \text {Uhr}$ bis $18 \, \text {Uhr}$ dazukommen. Also in $8 \,\text {h} - 2,5 \, \text{h} = 5,5 \text{h}$ . Folglich kannst du die Änderungsrate mit

$\dfrac{8,58 \, \text{cm}}{5,5 h} = 1,56 \, \dfrac{\text{cm}}{\text{h}}$

Also müssen die Schneekanonen $1,56\, \dfrac{\text{cm}}{\text{h}}$ zusätzlich liefern.

Aufgabe A 2.2

$\blacktriangleright$ Länge der Diagonalen berechnen

Du sollst die Länge der Diagonalen $d$ und $e$ einer Raute berechnen, die mithilfe der Funktion $g_3$ konstruiert wird.

Grafik mit einer Kurve und einem Rechteck, das durch Linien und Punkte dargestellt wird. Achsen beschriftet mit x und y.

Abb. 6: Die Diagonalen $d$ und $e$ schneiden sich gegenseitig in der Mitte. Der Punkt P ist der höchste Punkt der Funktion und liegt bei $(3 \mid 0)$ .

Zunächst setzt du $a = 3$ in die Funktionenschar $g_a$ ein und erhältst die Funktion

$g_3(x) = 3 \cdot \mathrm \cos (3 \cdot x) \,\,\,\,\,\,$ für $\,\,\,\, - \frac{\pi}{6} \leq x \leq \frac{\pi}{6}$

Die y - Koordinate des Schnittpunkts mit der y - Achse erhälst du über den Funktionswert für $x = 0$ .

$g_3(0) = 3$

Also ist der erste Diagonalvektor der Vektor, der von $(0 \mid 0)$ auf den Punkt $(0 \mid 3)$ zeigt:

$\vec{d} = \pmatrix{0 \\ 3}$

Die Länge dieses Vektors beträgt $\sqrt{0^2 + 3^2}$ = $3 \, \text{LE}$ . Für die andere Diagonale nutzt du die Eigenschaft, dass die Diagonalen einer Raute einander genau in der Hälfte der Strecke schneiden. Das heißt, im Punkt $(0 \mid 1,5)$ schneiden sich die beiden Diagonalen dieser Raute. Du weißt, dass die beiden Eckpunkte des Diagonalvektors $\vec{e}$ auf der Funktion $g_3$ liegen.

Folglich musst du nun die Schnittpunkte der Funktion $y = 1.5$ mit der Funktion $g_3$ bestimmen:

$\begin{array}[t]{rll} & x&=& 0,35 &\quad \end{array}$

Vollständige Lösung anzeigen

Wegen $\mathrm{\cos(-a)} = \mathrm{\cos(a)}$ und dem Definitionsbereich der Funktion musst du noch beachten, dass zu dieser Lösung noch der negative Wert dazukommt.

Also sind deine Schnittpunkte $(-0,35 \mid 0)$ und $(0,35\mid 0)$ .

Diese beiden Punkte verbindet der zweite Diagonalvektor, also der Vektor

$\pmatrix{0,35 -0.35 \\ 0 - 0}= \vec{e} = \pmatrix{-0,7 \\ 0}$

Er hat die Länge $0,7 \, \text{LE}$ .

$\blacktriangleright$ Parameter berechnen

In diesem Aufgabenteil musst du $a$ so berechnen, dass die Raute ein Quadrat ist. Für ein Quadrat gilt, dass seine beiden Diagonalen gleich lang sind. Es ist hilfreich, sich auch hier eine Skizze zu machen.

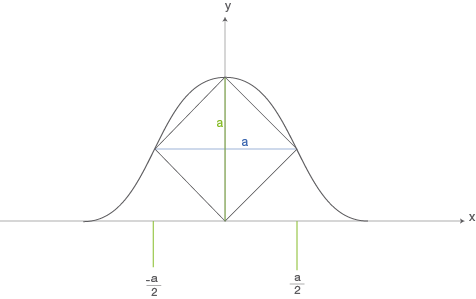Mathematische Darstellung einer Funktion mit einem Rechteck und Achsen.

Abb. 7: Die Funktion g berührt die Raute genau an den Punkten $(\frac{a}{2} \mid \frac{a}{2})$ und $(-\frac{a}{2} \mid \frac{a}{2})$ . Du musst im Folgenden nur mit einem der Punkte rechnen, weil die Punkte an der y - Achse gespiegelt sind und es gilt $\mathrm{\cos(-a)} = \mathrm{\cos(a)}$ .

Du weißt also, dass gelten muss: $g_a(\frac{a}{2}) = \frac{a}{2}$ . Beim Auflösen der Gleichung beschränkst du dich nur auf positive Lösungen (die Diagonalen können nur eine positive Länge haben):

$\begin{array}[t]{rll} &a &\approx& 1,45 &\quad \scriptsize \end{array}$

Vollständige Lösung anzeigen

Also ist die Raute ungefähr für den Wert $a = 1,45$ ein Quadrat.

Bildnachweise [nach oben]

[1-8]

Aufgabe A 2.1

$\blacktriangleright$ Extrempunkt bestimmen

Du hast die Funktion $s(t) = 16 \cdot \mathrm e^{-0,5t} - 14 \cdot \mathrm e^{-t} - 2$ gegeben.

Lass dir dazu den Graphen anzeigen. Der Befehl zur Bestimmung von Maxima lautet:

SHIFT $\to$ GSOLVE $\to$ MAX

Du erhältst als gerundete Werte die folgenden Koordinaten:

$\quad \text{H} \, (1,12 \mid 2,57)$

Diagramm einer mathematischen Funktion mit Achsenbeschriftungen und Maximalwert.

Abb. 1: Maximum von $s$

Nun musst du noch ausschließen, dass der Graph auf dem Rand seines Definitionsbereichs ein Maximum annimmt.

Du erkennst so, dass die maximale momentane Änderungsrate der Schneehöhe ungefähr $2,6 \, \dfrac{\text{cm}}{\text{h}}$ beträgt.

$\blacktriangleright$ Intervall mit nach unten beschränktem Wachstum berechnen

Lass dir dazu die Funktion $s$ mit der konstanten Funktion $y = 2$ anzeigen und bestimme ihre Schnittpunkte.

Schnittpunkte bestimmst du mit:

SHIFT $\to$ GSOLVE $\to$ ISCT

Du erhältst folgende Koordinaten:

$P_1 \, (1,99 \mid 2)$ $\quad P_2 \, (0,51 \mid 2)$

Graph einer mathematischen Funktion mit zwei Kurven und einem Schnittpunkt. Koordinaten sind angegeben.

Abb. 2: Erster Schnittpunkt von $s$ und $y$

Das Intervall, in dem $s$ größer ist als die Konstante $2$ , wird von den Schnittpunkten begrenzt. Jetzt ist nur noch wichtig, die $t$ - Werte in Stunden umzurechnen.

Also ist die momentane Änderungsrate im Intervall zwischen ca $10: 30 \,\text{Uhr}$ und $12 \, \text{Uhr}$ größer als $2 \, \dfrac{\text{cm}}{\text{h}}$ .

$\blacktriangleright$ Schneehöhe bestimmen

$S‘ = s$

$\displaystyle\int_{0}^{2}s(t) \, \mathrm dt$

$\blacktriangleright$ Integralfreien Funktionsterm bestimmen

Bestimme also zunächst die allgemeinen Stammfunktionen von $s$ :

$c$ muss nun so gewählt werden, dass $S_c(t) =150$ ist:

Die Funktion $S(t) = -32 \mathrm e^{-0,5t} + 14 \mathrm e^{-t} -2t + 168$ beschreibt also die Schneehöhe zum Zeitpunkt $t$ .

$\blacktriangleright$ Uhrzeiten mit einer Schneehöhe von $\boldsymbol{153\,\text{cm}}$ bestimmen

Dafür kannst du deinen Taschenrechner verwenden, indem du wie zuvor den Schnittpunkt des Graphen von $S$ mit der Gerade zu $y = 153$ bestimmst. Du erhältst dann folgende Lösung:

$t_1 \approx -0,80$ $\quad$ $t_2 \approx 1,50$ $\quad$ $t_3 \approx 7,03$

Da die Messung bei $t=0$ startet, fällt $t_1$ weg. Der Schnee ist also um ca. $11.30$ Uhr und $17$ Uhr $153\,\text{cm}$ hoch.

$\blacktriangleright$ Zusätzliche Schneezunahme mit einer Schneekanone berechnen

$F(t) = s(t) + 1 = 16 \mathrm e^{-0,5t} -14e^{-t} - 1$

Gefragt ist nun, um wie viele Stunden diese Maßnahme den Zeitraum verlängert, in dem die Schneehöhe zunimmt.

Den Befehl für die Bestimmung von Nullstellen findest du unter:

SHIFT $\to$ GSOLVE $\to$ ROOT

Diagramm einer mathematischen Funktion mit einer Kurve und einer Wurzelstelle.

Abb. 4: Nullstelle von $F$

Grafik einer mathematischen Funktion mit einer Wurzel und einer exponentiellen Kurve.

6 Abb. 5: Nullstelle von $s$

Diese Nullstellen ziehst du voneinander ab, also $5,43 - 3,88 = 1,65$ . Also verlängert sich der Zeitraum, in dem die Schneehöhe zunimmt, um ca $1,5$ Stunden.

$\,$

$\blacktriangleright$ Geforderten Schneezuwachs berechnen

$S(8)= 151,42$

$\dfrac{8,58 \, \text{cm}}{5,5 h} = 1,56 \, \dfrac{\text{cm}}{\text{h}}$

Also müssen die Schneekanonen $1,56\, \dfrac{\text{cm}}{\text{h}}$ zusätzlich liefern.

Aufgabe A 2.2

$\blacktriangleright$ Länge der Diagonalen berechnen

Du sollst die Länge der Diagonalen $d$ und $e$ einer Raute berechnen, die mithilfe der Funktion $g_3$ konstruiert wird.

Abb. 6: Die Diagonalen $d$ und $e$ schneiden sich gegenseitig in der Mitte. Der Punkt P ist der höchste Punkt der Funktion und liegt bei $(3 \mid 0)$ .

Zunächst setzt du $a = 3$ in die Funktionenschar $g_a$ ein und erhältst die Funktion

$g_3(x) = 3 \cdot \mathrm \cos (3 \cdot x) \,\,\,\,\,\,$ für $\,\,\,\, - \frac{\pi}{6} \leq x \leq \frac{\pi}{6}$

Die y - Koordinate des Schnittpunkts mit der y - Achse erhälst du über den Funktionswert für $x = 0$ .

$g_3(0) = 3$

Also ist der erste Diagonalvektor der Vektor, der von $(0 \mid 0)$ auf den Punkt $(0 \mid 3)$ zeigt:

$\vec{d} = \pmatrix{0 \\ 3}$

Folglich musst du nun die Schnittpunkte der Funktion $y = 1.5$ mit der Funktion $g_3$ bestimmen:

$\begin{array}[t]{rll} & x&=& 0,35 &\quad \end{array}$

Vollständige Lösung anzeigen

Wegen $\mathrm{\cos(-a)} = \mathrm{\cos(a)}$ und dem Definitionsbereich der Funktion musst du noch beachten, dass zu dieser Lösung noch der negative Wert dazukommt.

Also sind deine Schnittpunkte $(-0,35 \mid 0)$ und $(0,35\mid 0)$ .

Diese beiden Punkte verbindet der zweite Diagonalvektor, also der Vektor

$\pmatrix{0,35 -0.35 \\ 0 - 0}= \vec{e} = \pmatrix{-0,7 \\ 0}$

Er hat die Länge $0,7 \, \text{LE}$ .

$\blacktriangleright$ Parameter berechnen

$\,$

$\begin{array}[t]{rll} &a &\approx& 1,45 &\quad \scriptsize \end{array}$

Vollständige Lösung anzeigen

Also ist die Raute ungefähr für den Wert $a = 1,45$ ein Quadrat

Bildnachweise [nach oben]

[1-8]