Wahlaufgaben (W1-W6)

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ und $g$ . Der Graph von $f$ ist symmetrisch bezüglich der $y$ -Achse, der Graph von $g$ ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt $(2\mid 1).$

Gib für die Graphen von $f$ und $g$ jeweils die Koordinaten und die Art eines weiteren Extrempunkts an.

(2 BE)

Untersuche die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x)=f(x) \cdot(g(x))^{3}$ im Hinblick auf eine mögliche Symmetrie ihres Graphen.

(3 BE)

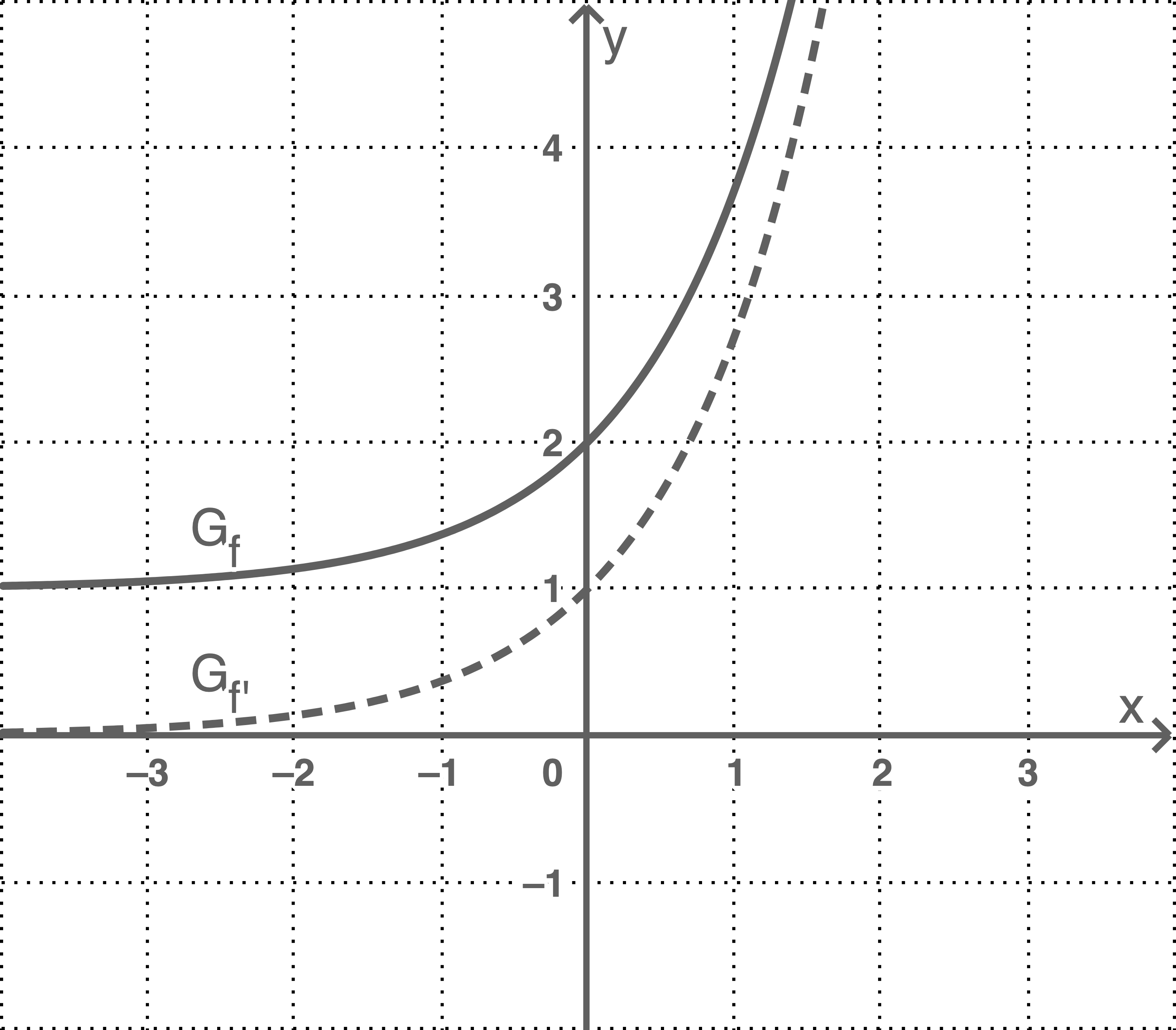
Die Abbildung zeigt den Graphen $G_f$ einer in $\mathbb{R}$ definierten Funktion $f$ sowie den Graphen der ersten Ableitungsfunktion von $f$ .

Gib die Steigung der Tangente an $G_f$ im Punkt $\left(0\mid f(0)\right)$ an.

(1 BE)

Betrachtet wird die Schar der Funktionen $g_c$ mit $c \in \mathbb{R}^+$ . Der Graph $g_c$ geht aus $G_f$ durch Streckung mit dem Faktor $c$ in $y$ -Richtung hervor. Die Tangente an den Graphen von $g_c$ im Punkt $\left(0\mid g_c(0)\right)$ schneidet die $x$ -Achse.
Bestimme rechnerisch die $x$ -Koordinate des Schnittpunkts.

(4 BE)

Gegeben sind die Punkte $A\left(0\mid0\mid0\right)$ , $B\left(3\mid4\mid1\right)$ , $C\left(1\mid7\mid3\right)$ und $D\left(-2\mid3\mid2\right)$ .

Weise nach, dass das Viereck $ABCD$ ein Parallelogramm ist.

(1 BE)

Der Punkt $T$ liegt auf der Strecke $\overline{AC}$ . Das Dreieck $ABT$ hat bei $B$ einen rechten Winkel.
Ermittle das Verhältnis der Länge der Strecke $\overline{AT}$ zur Länge der Strecke $\overline{CT}$ .

(4 BE)

Gegeben sind der Punkt $P(-1\mid 7\mid 2)$ und die Ebene $E:x_1+3x_2=0.$

Zeige, dass der Punkt $P$ nicht in $E$ liegt.

(1 BE)

Bestimme die Koordinaten des Punktes, der entsteht, wenn $P$ an $E$ gespiegelt wird.

(4 BE)

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n=100$ und $p.$
Der Erwartungswert von $X$ ist 50.

Berechne die Standardabweichung von $X.$

(3 BE)

Die Wahrscheinlichkeit $P(X\geq 61)$ beträgt etwa 2 %.
Bestimme damit einen Näherungswert für die Wahrscheinlichkeit $P(40\leq X\leq 60).$

(2 BE)

In einem Behälter befinden sich Kugeln, von denen jede dritte gelb ist.

Aus dem Behälter wird zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt.
Berechne die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind.

(1 BE)

Im Behälter werden zwei gelbe Kugeln durch zwei blaue Kugeln ersetzt. Anschließend wird aus dem Behälter erneut zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind, beträgt nun $\dfrac{1}{16}.$
Ermittle, wie viele gelbe Kugeln sich nach dem beschriebenen Vorgang im Behälter befinden.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Da der Graph von $f$ symmetrisch bezüglich der $y$ -Achse ist, existiert ein weiterer Hochpunkt des Graphen in $(-2 \mid 1).$
Aufgrund der Punktsymmetrie bezüglich des Koordinatenursprungs hat der Graph von $g$ einen Tiefpunkt in $(-2 \mid -1).$

Wegen der Symmetrien der Graphen von $f$ und $g$ gilt :

$\begin{array}[t]{rll} f(-x) &=&f(x) &\quad \scriptsize \\[5pt] g(-x) &=&-g(x) &\quad \scriptsize \\[5pt] \end{array}$

Damit folgt für die Symmetrie des Graphen von $h$ :

$h(-x)=f(-x)\cdot (g(-x))^3$ $=f(x)\cdot (-g(x))^3=-f(x)\cdot(g(x))^3$ $=-h(x)$

Der Graph von $h$ ist symmetrisch zum Koordinatenursprung.

Die Steigung der Tangente an $G_f$ im Punkt $(0 \mid f(0))$ wird durch $\(f$ beschrieben. Dieser Wert lässt sich in der gegebenen Abbildung ablesen und beträgt $1.$

1. Schritt: Tangente im Punkt $(0 \mid g_c(0))$ bestimmen
Da für die Funktion $g_c$ die Funtkion $f$ um den Faktor $c$ in $y$ -Achsenrichtung gestreckt wird, gilt $g_c(x) = c \cdot f(x)$ und $\(g_c$ Damit gilt für die Tangente:

$\( y = g_c$ $\(= c \cdot f$ $= c \cdot 1 \cdot x + c \cdot 1 = c \cdot x + 2 c$

2. Schritt: $x$ -Koordinate des Schnittpunkts berechnen

$\begin{array}[t]{rlll} cx+2c&=& 0 & \quad \scriptsize \mid -2c\\[5pt] cx&=& -2c & \quad \scriptsize \mid :c\\[5pt] x&=& -2 & \quad \scriptsize \\[5pt] \end{array}$

Damit beträgt die $x$ -Koordinate des Schnittpunktes der Tangente mit der $x$ -Achse $x =-2.$

Ein Viereck ist ein Parallelogramm, wenn die gegenüberliegenden Seiten parallel sind. Dies ist schon der Fall, wenn zwei der Seiten gleich lang und parallel sind. Damit folgt:

$\overrightarrow{AB} = \left(\pmatrix{3\\4\\0}-\pmatrix{0\\0\\0}\right) = \pmatrix{3\\4\\1}$

$\overrightarrow{DC} = \left(\pmatrix{1\\7\\3} -\pmatrix{-2\\3\\2}\right) = \pmatrix{3\\4\\1}$

Da $\overrightarrow{AB} = \overrightarrow{DC}$ gilt, sind die Seiten $\overline{AB}$ und $\overline{DC}$ gleich lang und parallel. Damit ist das Viereck $ABCD$ ein Parallelogramm.

1. Schritt: Den Ortsvektor von $T$ bestimmen
$T$ hat den Ortsvektor $\lambda \cdot \overline{AC}$ mit $\lambda \in [0;1].$

$T=\lambda \cdot \overline{AC}$ $=\lambda \cdot \pmatrix{1-0\\7-0\\3-0}$ $=\pmatrix{\lambda\\7\lambda\\3\lambda}$

2. Schritt: Das Skalarprodukt von $\overrightarrow{AB}$ und $\overrightarrow{TB}$ gleich $0$ setzen.
Das Skalarprodukt der beiden Vektoren muss $0$ ergeben, da die Aufgabenstellung für das Dreieck $ABT$ bei $B$ einen rechten Winkel fordert.

$\lambda = \frac{13}{17}$

Vollständige Lösung anzeigen

Somit gilt $\overline{AT} = \frac{13}{17} \cdot \overline{AC}$ . Daraus folgt $\overline{TC} = \frac{4}{17} \cdot \overline{AC}.$
Damit lautet das Verhältnis zwischen diesen beiden Strecken $13:4.$

Einsetzen des Punktes $P$ in die Ebenengleichung liefert:

$\begin{array}[t]{rll} x_1+3x_2 &=&0 &\quad \scriptsize \\[5pt] -1+3\cdot 7 &\not =&0&\quad \scriptsize \\[5pt] 20 &\not =&0&\quad \scriptsize \\[5pt] \end{array}$

Damit liegt der Punkt $P$ nicht in der Ebene $E.$

1. Schritt: Normalenvektor ablesen

Ein Normalenvektor der Ebene $E$ ist gegeben durch $\overrightarrow{n}=\pmatrix{1\\3\\0}.$

2. Schritt: Gleichung der Gerade die senkrecht zu $E$ durch $P$ verläuft, aufstellen

$g: \overrightarrow{x} = \pmatrix{-1\\7\\2}+t \cdot \pmatrix{1\\3\\0}$

3. Schritt: Schnittpunkt von $g$ und $E$ berechnen

Für den Schnittpunkt muss $g$ und $E$ einsetzt werden.

Vollständigen Rechenweg anzeigen

$t=-2$

Dieses $t$ müsste für den Schnittpunkt in $g$ eingesetzt werden. Da jedoch nicht nach dem Schnittpunkt, sondern nach dem Spiegelpunkt gefragt ist, muss das doppelte von $t$ eingesetzt werden. Die Strecke von $P$ zu $E$ und von $E$ zum Spiegelpunkt sind gleich lang.

4. Schritt: Spiegelpunkt $\(P$ berechnen

$\(P$ $=\pmatrix{-5\\-5\\2}$

Die Koordinaten des gesuchten Punkts sind $\(P$ .

Um die Standardabweichung zu berechnen, muss zuerst $p$ ermittelt werden. Es gilt:

$\begin{array}[t]{rll} E(X)&=& 50 &\quad \scriptsize \\[5pt] 100\cdot p&=& 50 &\quad \scriptsize \mid\;:100 \\[5pt] p&=& 0,5 &\quad \scriptsize \\[5pt] \end{array}$

Damit ist die Standardabweichung gegeben durch $\sigma(X)= \sqrt{100 \cdot 0,5^2}=5.$

Für $p=0,5$ ist die Binomialverteilung symmetrisch um den Erwartungswert $E(X)=50.$
Damit gilt $P(X \geq 61)=P(X\leq 39)\approx 2\%.$

Daraus folgt:

Vollständigen Rechenweg anzeigen

$P(40\le X\le 60)=96\%$

Ein Näherungswert für die gesuchte Wahrscheinlichkeit ist $96\%.$

Die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, beträgt $p=\dfrac{1}{3}.$ Die Wahrscheinlichkeit dafür, dass zwei hintereinander gezogene Kugeln gelb sind, ist dann gegeben durch $\dfrac{1}{3} \cdot \dfrac{1}{3} = \dfrac{1}{9}.$

Für die Wahrscheinlichkeit $\(p$ eine gelbe Kugel zu ziehen, gilt $\(p$ und damit $\(p$ Daraus lässt sich folgern, dass jede vierte Kugel gelb ist.

$x$ ist die gesuchte Anzahl an gelben Kugeln nach dem Tausch. Dann liegen insgesamt $4\cdot x$ Kugeln im Behälter.
Vor dem Tausch mit den blauen Kugeln, gab es zwei gelbe Kugeln mehr, also ingesamt $x+2$ . Die Wahscheinlichkeit vor dem Tausch eine gelbe Kugel zu ziehen, ist damit $p=\frac{x+2}{4x}$ . Aus der Aufgabenstellung ist außerdem bekannt, dass vor dem Tausch jede dritte Kugel gelb war, also dass $p=\frac{1}{3}$ ist. Durch Gleichsetzten der Wahrscheinlichkeit $p$ ergibt sich $x$ .

$\begin{array}[t]{rll} \dfrac{x+2}{4\cdot x}&=&\dfrac{1}{3} &\quad \scriptsize \mid\; \cdot (4\cdot x) \; \mid\; \cdot 3\\[5pt] 3x+6&=&4\cdot x &\quad \scriptsize \mid\;-3x \\[5pt] 6&=&x \end{array}$

Nach dem beschriebenen Vorgang befinden sich $6$ gelbe Kugeln im Behälter.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?