Pflichtteil 2

Aufgabe 1

Gegeben ist die Funktion $f$ mit $f(x)= \mathrm e^{0,5x^2}.$
Bestimme den Wert der zweiten Ableitung von $f$ an der Stelle $x_0=0$ .

(2,5 VP)

Aufgabe 2

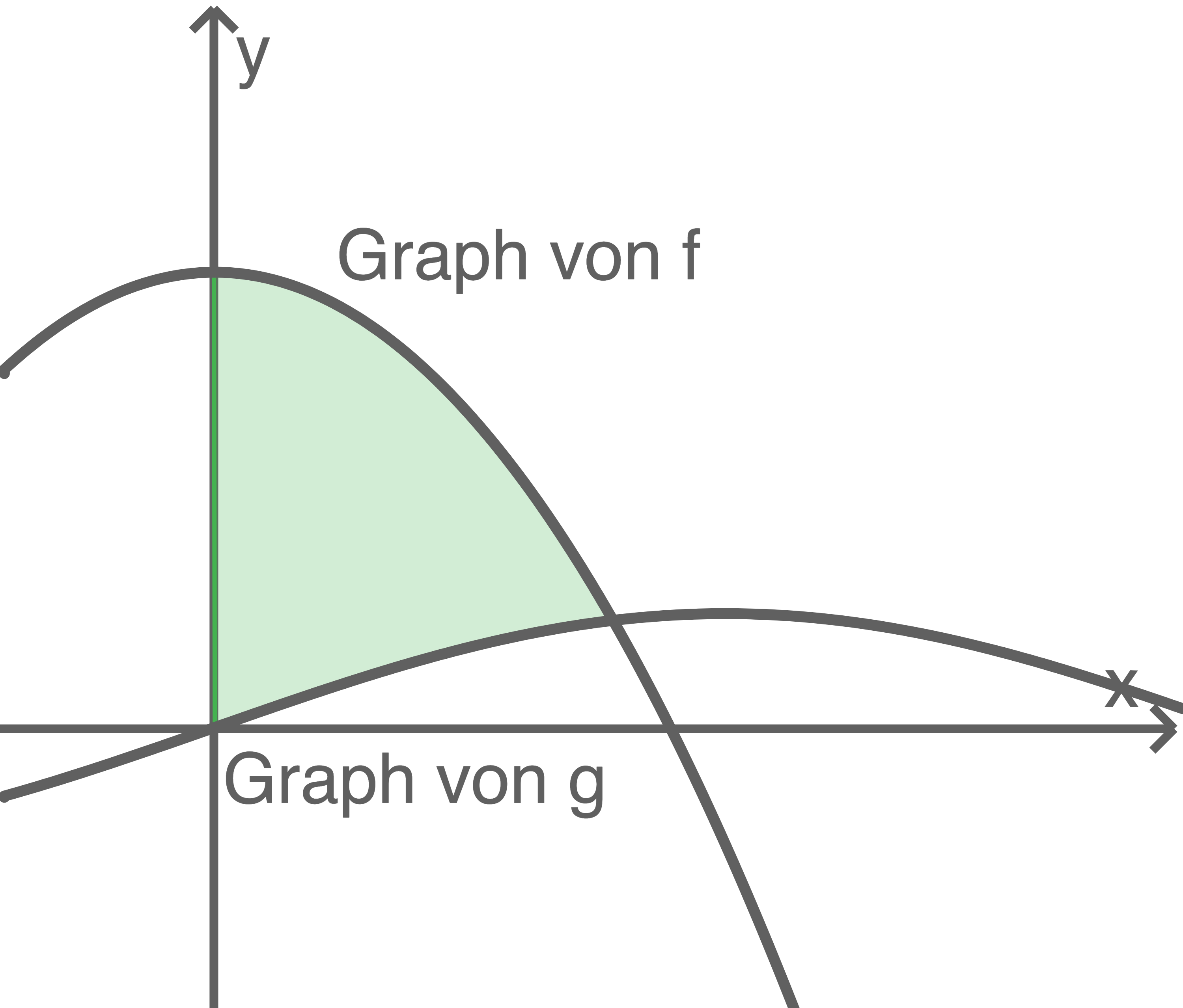
Abgebildet sind die Graphen der Funktionen $f$ und $g$ mit $f(x)=4-3x^2$ und $g(x)=\sin \left(\dfrac{\pi}{2}x \right).$

Zeige, dass sich die beiden Graphen an der
Stelle $x_0=1$ schneiden.

(0,5 VP)

Berechne den Inhalt der markierten Fläche.

(2 VP)

Aufgabe 3

Der Graph $G_f$ der Funktion $f$ besitzt den Tiefpunkt $T(1\mid -2)$ . Der Graph der Funktion $g$ mit $g(x)=\dfrac{1}{9}x^3-3x$ entsteht, indem $G_f$ um $a$ Einheiten nach rechts und um $b$ Einheiten nach unten verschoben wird. Bestimme die Werte $a$ und $b.$

(2,5 VP)

Aufgabe 4

Die Graphen einer Schar ganzrationaler Funktionen dritten Grades berühren die $x$ -Achse im Punkt $O(0 \mid 0).$ Jeder Graph der Schar besitzt die Extremstelle $x_0=-2.$
Untersuche, ob alle Graphen der Schar den Punkt $P(-3 \mid 0)$ gemeinsam haben.

(2,5 VP)

Aufgabe 5

Gegeben sind die Ebene $E: 2x_1+3x_2-4x_3=12$ und für jedes $a\in \mathbb\ \mathbb{R}$ eine Gerade $g_a:\overrightarrow{x}=\pmatrix{-1\\5\\3} +t \cdot \pmatrix{a\\-5\\-4}, t\in \mathbb\ \mathbb{R}.$

Bestimme den Wert von $a$ , für den die Gerade $g_a$ parallel zu $E$ ist.

(1 VP)

Für jedes $a\in \mathbb\ \mathbb{R}$ ist $P_a$ der Schnittpunkt von $g_a$ mit der $x_1x_3$ -Ebene.
Bestimme den Wert von $a$ , für den $P_a$ in $E$ liegt.

(1,5 VP)

Aufgabe 6

Gegeben sind die parallelen Geraden $g:\overrightarrow{x}=\pmatrix{6\\5\\-2}+s\cdot \pmatrix{1\\4\\-1}, s\in \mathbb\ \mathbb{R},$ und $h:\overrightarrow{x}=\pmatrix{0\\-1\\4}+t\cdot \pmatrix{1\\4\\-1}, t\in \mathbb\ \mathbb{R}.$

Der Punkt $A(4 \mid -3 \mid0)$ liegt auf $g$ . Weise nach, dass $A$ derjenige Punkt auf $g$ ist, der vom Punkt $B(0 \mid -1 \mid 4)$ den kleinsten Abstand hat.

(1 VP)

Die Gerade $h$ ist die Bildgerade von $g$ bei einer Spiegelung an der Ebene $E.$
Ermittle eine Gleichung von $E.$

(1,5 VP)

Aufgabe 7

Ein Glücksrad besteht aus einem gelben, einem blauen und einem roten Sektor.
Wird das Glücksrad einmal gedreht, erscheint der gelbe Sektor mit der Wahrscheinlichkeit $\dfrac{1}{3}$ und der rote Sektor mit der Wahrscheinlichkeit $\dfrac{1}{2}.$

Berechne die Wahrscheinlichkeit dafür, dass bei zweimaligem Drehen der blaue Sektor zweimal erscheint.

(1 VP)

Beschreibe im Sachzusammenhang ein Zufallsexperiment und ein Ereignis, dessen Wahrscheinlichkeit sich mit dem Term $\pmatrix{\dfrac{1}{3}}^5+5\cdot \pmatrix{\dfrac{1}{3}}^4\cdot \dfrac{2}{3}$ berechnen lässt.

(1,5 VP)

Aufgabe 8

Gegeben sind die im Folgenden beschriebenen Zufallsgrößen $X$ und $Y$ :

Ein Würfel, dessen Seiten mit den Zahlen von 1 bis 6 durchnummeriert sind, wird zweimal geworfen. $X$ gibt die Summe der dabei gewürfelten Zahlen an.
Aus einem Behälter mit 60 schwarzen und 40 weißen Kugeln wird zwölfmal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. $Y$ gibt die Anzahl der entnommenen schwarzen Kugeln an.

Begründe, dass die Wahrscheinlichkeit $P(X=4)$ mit der Wahrscheinlichkeit $P(X=10)$ übereinstimmt.

(1 VP)

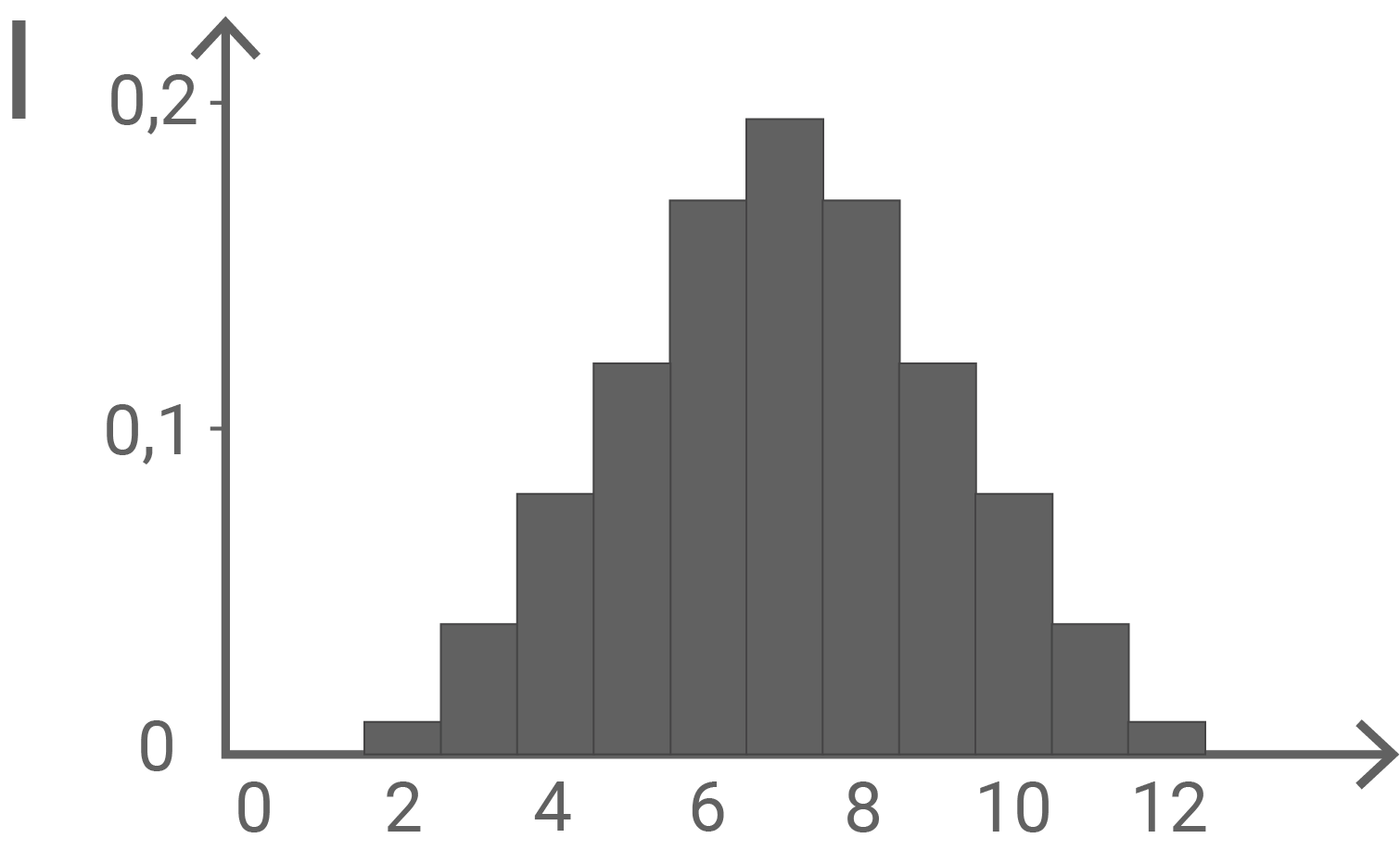
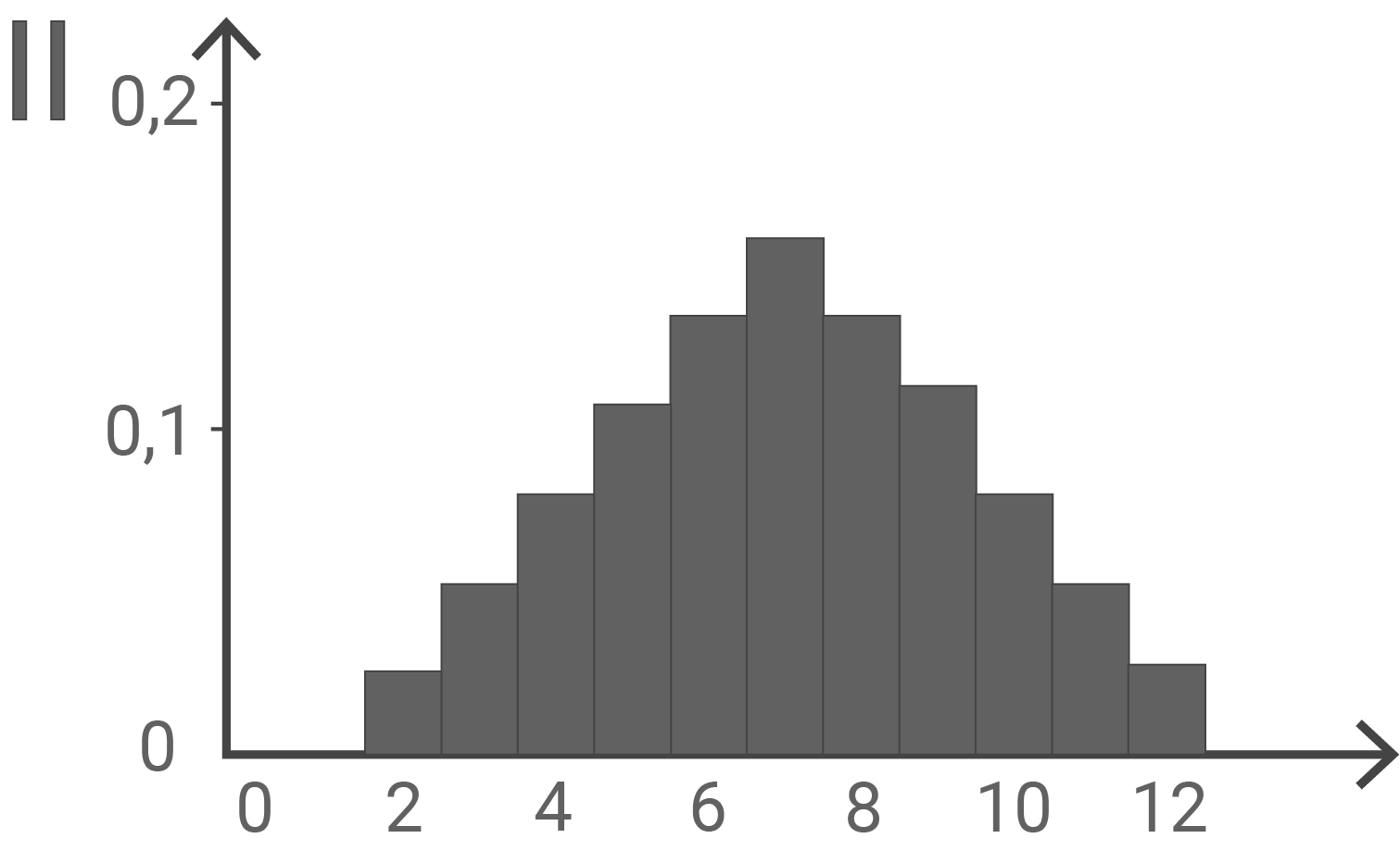
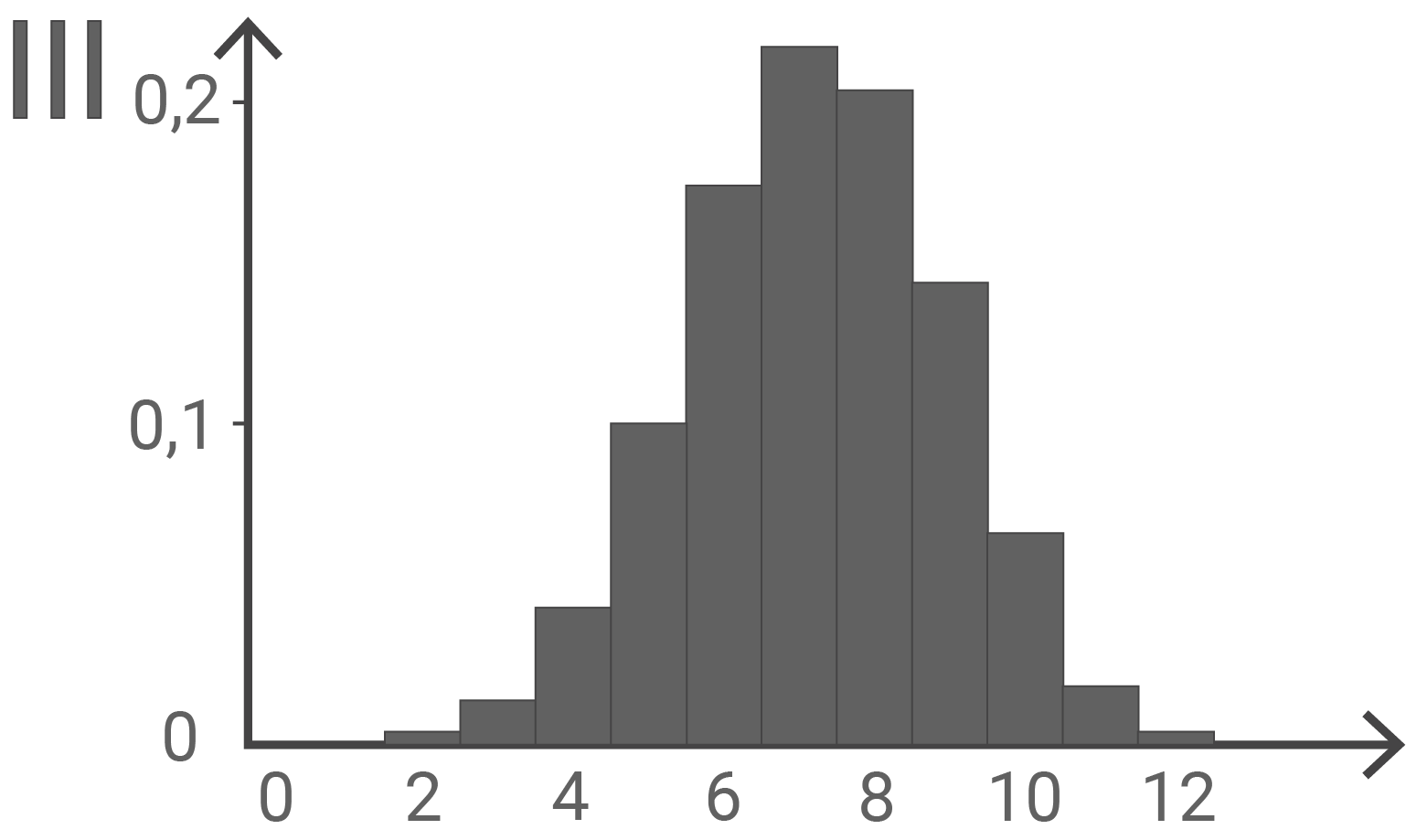
Die Wahrscheinlichkeitsverteilungen von $X$ und $Y$ werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordne $X$ und $Y$ jeweils dem passenden Diagramm zu und begründe deine Zuordnung.

(1,5 VP)

Histogramm mit grauen Balken, das die Verteilung von Werten auf einer x-Achse von 0 bis 12 zeigt.

Histogramm mit Häufigkeitsverteilung, x-Achse zeigt Werte von 0 bis 12, y-Achse zeigt Häufigkeiten von 0 bis 0,2.

Histogramm mit einer Verteilung von Werten auf der x-Achse und Wahrscheinlichkeiten auf der y-Achse.

Weiter lernen mit SchulLV Plus!

monatlich kündbarSchulLV Plus-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

1. Ableitung bilden:

Kettenregel:

$\(\begin{array}[t]{rll} f$

2. Ableitung bilden:

Kettenregel:

Rechenweg anzeigen

$\( f$

Wert bei $x_0=0$ berechnen:

$\(\begin{array}[t]{rll} f$

Lösung 2

$\begin{array}[t]{rll} f(1)&=& 4-3\cdot1^2 &\ \\[5pt] &=& 1 \end{array}$

$\begin{array}[t]{rll} g(1)&=& \sin\left(\dfrac{\pi}{2}\cdot1 \right) & \\[5pt] &=& 1 \end{array}$

Da $f(1)=g(1)=1$ gilt, schneiden sich die beiden Graphen im Punkt $(1\mid1)$ und somit auch an der Stelle $x_0=1.$

Rechenweg anzeigen

$A= 3-\dfrac{2}{\pi} \ [\text{FE}]$

Der Flächeninhalt der markierten Fläche beträgt somit $3-\dfrac{\pi}{2} [\text{FE}]$ .

Lösung 3

Berechnen der Koordinaten des Tiefpunkts von $g$

$\(g$

1.Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

2.Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(g$

Da $\(g$ und $\(g$ , befindet sich der Tiefpunkt von $g$ an der Stelle $x=3.$

$\begin{array}[t]{rll} g(3)&=& \dfrac{1}{9}\cdot3^3-3\cdot9& \\[5pt] &=& -6 \end{array}$

Die Koordinaten des Tiefpunkts von $g$ sind somit $T(3\mid-6).$

Verschiebung in $x$ - und $y$ -Richtung berechnen

Berechnen der Differenz zwischen $x$ - und $y$ -Werten der Tiefpunkte:

$\begin{array}[t]{rll} a&=& \mid3-1\mid & \\[5pt] &=&2 \end{array}$

$\begin{array}[t]{rll} b&=& \mid-6 -(-2)\mid &\ \\[5pt] &=&4 \end{array}$

Lösung 4

Funktionsgleichung einer ganzrationalen Funktion dritten Grades: $f(x)=ax^3+bx^2+cx+d$

Bestimmen von d:

Koordinaten des Berührpunktes $O(0\mid0)$ einsetzen:

$\begin{array}[t]{rll} 0&=&a\cdot0^3+b\cdot0^2+c\cdot0+d & \\[5pt] 0&=& d \end{array}$

Bestimmen von c:

Da $O$ ein Berührpunkt ist, gilt $\(f$ .

$\(f$

$\(\begin{array}[t]{rll} f$

Bestimmen von b:

Extremstelle bei $x_0=-2$ :

$\(\begin{array}[t]{rll} f$

Somit ergibt sich folgende Funktion:

$f(x)=ax^3+3ax^2$

$\begin{array}[t]{rll} f(-3)&=& -27a+27a & \\[5pt] &=&0 \end{array}$

Da die Funktion an der Stelle $x=-3$ unabhängig von $a$ immer $0$ ergibt, ist der Punkt $P(-3\mid0)$ in allen Graphen der Schar enthalten.

Lösung 5

Damit die Gerade $g_a$ parallel zur Ebene $E$ ist, muss der Richtungsvektor von $g$ orthogonal zu einem Normalenvektor von $E$ sein:

Skalarprodukt in Abhängigkeit von $a$ bilden:

Rechenweg anzeigen

$a=-0,5$

1. Schritt: Schnittpunkt von $g_a$ mit der $x_1x_3-$ Ebene berechnen

Koordinatenform der $x_1x_3-$ Ebene: $x_2=0$

Einsetzen der $x_2-$ Koordinate von $g_a$ ergibt:

$\begin{array}[t]{rll} 5-5t&=& 0 &\quad \scriptsize \mid\; +5t\\[5pt] 5&=& 5t &\quad \scriptsize \mid\; :5\\[5pt] 1&=& t \end{array}$

Durch Einsetzen von $t=1$ in $g_a$ folgt:

$\begin{array}[t]{rll} g_a:\overrightarrow{OP_a}&=& \pmatrix{-1\\5\\3}+1\cdot\pmatrix{a\\-5\\-4}& \\[5pt] &=& \pmatrix{-1+a\\5-5\\3-4}& \\[5pt] &=& \pmatrix{-1+a\\0\\-1}& \\[5pt] \end{array}$

$P_a(a-1\mid0\mid-1)$

2. Schritt: $P_a$ in $E$ einsetzen und nach a auflösen

Rechenweg anzeigen

$a=5$

Lösung 6

Da $B$ auf der Geraden $h$ liegt, muss die Strecke $\overline{AB}$ orthogonal zur Geraden $h$ liegen, sodass $A$ den kleinsten Abstand zu $B$ hat:

Nachweis der Orthogonalität durch das Skalarprodukt:

Rechenweg anzeigen

$\overrightarrow{AB}\circ \pmatrix{1\\4\\-1}=0$

Ein Normalenvektor der Ebene $E$ ist gegeben durch $\overrightarrow{AB}.$

Da an $E$ gespiegelt wird, liegt der Mittelpunkt $M$ der Strecke $\overrightarrow{AB}$ in $E:$

$\begin{array}[t]{rll} \overrightarrow{OM}&=& \overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AB}&\ \\[5pt] &=& \pmatrix{4\\-3\\0}+\dfrac{1}{2}\cdot\pmatrix{-4\\2\\4}&\ \\[5pt] &=& \pmatrix{4\\-3\\0}+\pmatrix{-2\\1\\2}&\ \\[5pt] &=&\pmatrix{2\\-2\\2} \end{array}$

Damit ergibt sich folgende Koordinatengleichung:

$\begin{array}[t]{rll} E:-4x_1+2x_2+4x_3&=& c& \\[5pt] -4\cdot2+2\cdot(-2)+4\cdot2&=& c& \\[5pt] -8-4+8&=& c& \\[5pt] -4&=&c \end{array}$

$\begin{array}[t]{rll} E: -4x_1+2x_2+4x_3 &=& -4& \\[5pt] \end{array}$

Lösung 7

1. Schritt: Wahrscheinlichkeit des blauen Sektors berechnen

$\begin{array}[t]{rll} P\text{(blau)}&=&1- P\text{(gelb)}-P(\text{rot}) & \\[5pt] &=&1-\dfrac{1}{3}-\dfrac{1}{2} & \\[5pt] &=&\dfrac{6}{6}-\dfrac{2}{6}-\dfrac{3}{6} & \\[5pt] &=&\dfrac{1}{6} \end{array}$

2. Schritt: Wahrscheinlichkeit, dass zwei mal der blaue Sektor erscheint, berechnen:

Pfadregel (Produktregel) :

$P(bb)= \dfrac{1}{6}\cdot\dfrac{1}{6}=\dfrac{1}{36}$

Zufallsexperiment:

Das Glücksrad wird fünfmal gedreht.

Ereignis:

Es erscheint mindestens viermal der gelbe Sektor.

Lösung 8

$\begin{array}[t]{rll} P(X=4)&=& P({(1;3),(2;2),(3;1)})& \\[5pt] &=& 3\cdot\left(\dfrac{1}{6}\cdot\dfrac{1}{6}\right)& \\[5pt] &=&\dfrac{3}{36} \end{array}$

$\begin{array}[t]{rll} P(X=10)&=& P({(4;6),(5;5),(6;4)})& \\[5pt] &=& 3\cdot\left(\dfrac{1}{6}\cdot\dfrac{1}{6}\right)& \\[5pt] &=&\dfrac{3}{36} \end{array}$

Wahrscheinlichkeitsverteilung $Y:$ Diagramm III

Da in dem Behälter mehr schwarze als weiße Kugeln enthalten sind, muss die Verteilung asymmetrisch sein. Dies ist nur im Diagramm III der Fall.

Wahrscheinlichkeitsverteilung $X:$ Diagramm II

Betrachten eines Beispielwertes:

$\begin{array}[t]{rll} P(X=3)&=& P({(1;2),(2;1)}) & \\[5pt] &=& \dfrac{2}{36} \end{array}$

Da die Wahrscheinlichkeit $P(X=4)$ (in $a$ berechnet) nicht doppelt so groß wie $P(X=3)$ ist, kann das Diagramm I ausgeschlossen werden. Die Wahrscheinlichkeitsverteilung von $X$ wird dementsprechend im Diagramm II dargestellt.

Weiter lernen mit SchulLV Plus!

monatlich kündbarSchulLV Plus-Vorteile im ÜberblickDu hast bereits einen Account?