Analysis
Aufgabe I 1.1
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  durch
durch  mit
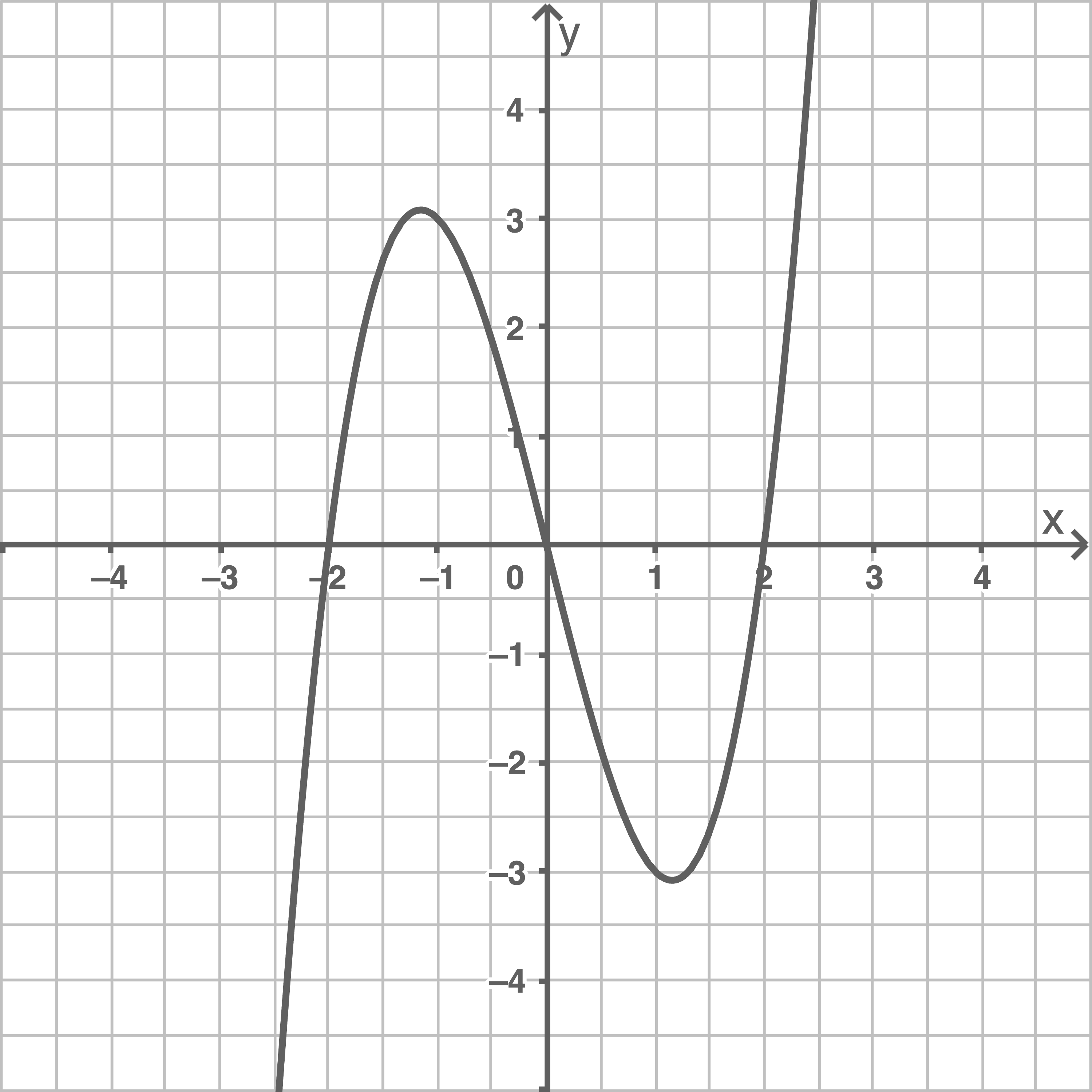
mit  Die Abbildung zeigt den Graphen einer der Funktionen der Schar.
Die Abbildung zeigt den Graphen einer der Funktionen der Schar.
a)
Begründe, dass jeder Graph der Schar symmetrisch bezüglich des Koordinatenursprungs ist.
(2 BE)
b)
Weise in Abhängigkeit von  und
und  nach, dass der Graph von
nach, dass der Graph von  einen Tiefpunkt mit der
einen Tiefpunkt mit der  -Koordinate
-Koordinate  hat.
Begründe, dass er zudem einen Hochpunkt besitzt und dass dieser eine kleinere
hat.
Begründe, dass er zudem einen Hochpunkt besitzt und dass dieser eine kleinere  -Koordinate hat als der Tiefpunkt.
-Koordinate hat als der Tiefpunkt.
(6 BE)
c)
Es gibt eine Funktion der Schar, die bei  eine Nullstelle hat und deren Graph im vierten Quadranten mit der
eine Nullstelle hat und deren Graph im vierten Quadranten mit der  -Achse ein Flächenstück mit dem Inhalt 40,5 einschließt.
Bestimme die zugehörigen Werte von
-Achse ein Flächenstück mit dem Inhalt 40,5 einschließt.
Bestimme die zugehörigen Werte von  und
und 
Die Funktion der Schar, deren Graph in der Abbildung dargestellt ist, wird mit
(7 BE)
d)
Die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse und die Gerade
-Achse und die Gerade  mit der Gleichung
mit der Gleichung  schließen ein Dreieck ein.
Berechne seinen Flächeninhalt.
schließen ein Dreieck ein.
Berechne seinen Flächeninhalt.
(7 BE)
e)
Begründe, dass die folgende Aussage richtig ist:
Ist  ein beliebiger Punkt auf dem Graphen von
ein beliebiger Punkt auf dem Graphen von  so liegt der Mittelpunkt der Verbindungsstrecke von
so liegt der Mittelpunkt der Verbindungsstrecke von  und dem Koordinatenursprung auf dem Graphen der in
und dem Koordinatenursprung auf dem Graphen der in  definierten Funktion
definierten Funktion  mit
mit 
(4 BE)
Aufgabe I 1.2
Die Leitung eines großen Unternehmens versendet jeden Arbeitstag um 7:00 Uhr eine E-Mail mit tagesaktuellen Informationen an alle Mitarbeiterinnen und Mitarbeiter. Diese wurden gebeten, nach dem Lesen der E-Mail eine Lesebestätigung zu versenden. Die folgende Tabelle zeigt für einen bestimmten Tag, wie viele Lesebestätigungen bei der Leitung des Unternehmens bis zum jeweiligen Zeitpunkt bereits eingegangen sind.| Zeitpunkt | Anzahl der bis dahin eingegangenen Lesebestätigungen |
|---|---|
| ..... | |
| ..... |
a)
Ermittle mit Hilfe der Tabelle für den betrachteten Tag, wie viele Lesebestätigungen im Zeitraum von 8:30 Uhr bis 10:00 Uhr im Mittel pro Stunde eingegangen sind.
Auf der Grundlage der über viele Tage erfassten Lesebestätigungen wurde mit Hilfe der in
(3 BE)
b)
Berechne  und interpretiere das Ergebnis im Sachzusammenhang.
und interpretiere das Ergebnis im Sachzusammenhang.
(3 BE)
c)
Es gilt  Begründe, dass die Funktion
Begründe, dass die Funktion  nicht geeignet ist, die momentane Änderungsrate auch für den Zeitraum nach 15:00 Uhr zu beschreiben.
nicht geeignet ist, die momentane Änderungsrate auch für den Zeitraum nach 15:00 Uhr zu beschreiben.
(3 BE)
d)
Berechne mit Hilfe der Funktion  die Anzahl der im Zeitraum von 10:00 Uhr bis 15:00 Uhr eines Arbeitstages eingegangenen Lesebestätigungen.
Ermittle, um wie viel Prozent diese auf der Grundlage des Modells berechnete Anzahl von der entsprechenden Anzahl des eingangs betrachteten Tages (vgl. Tabelle) abweicht.
die Anzahl der im Zeitraum von 10:00 Uhr bis 15:00 Uhr eines Arbeitstages eingegangenen Lesebestätigungen.
Ermittle, um wie viel Prozent diese auf der Grundlage des Modells berechnete Anzahl von der entsprechenden Anzahl des eingangs betrachteten Tages (vgl. Tabelle) abweicht.
(5 BE)
Aufgabe I 2.1
Zur Untersuchung der Lungenfunktion muss eine Person tief einatmen und anschließend zügig in ein Messgerät ausatmen. Die Änderungsrate des Luftvolumens pro Zeiteinheit beim Ausatmen heißt Atemfluss.
Bei einer Messung wird der Atemfluss für  näherungsweise durch die Funktion
näherungsweise durch die Funktion  mit
mit  beschrieben (t in Sekunden seit Beginn des Ausatmens,
beschrieben (t in Sekunden seit Beginn des Ausatmens,  in Liter pro Sekunde).
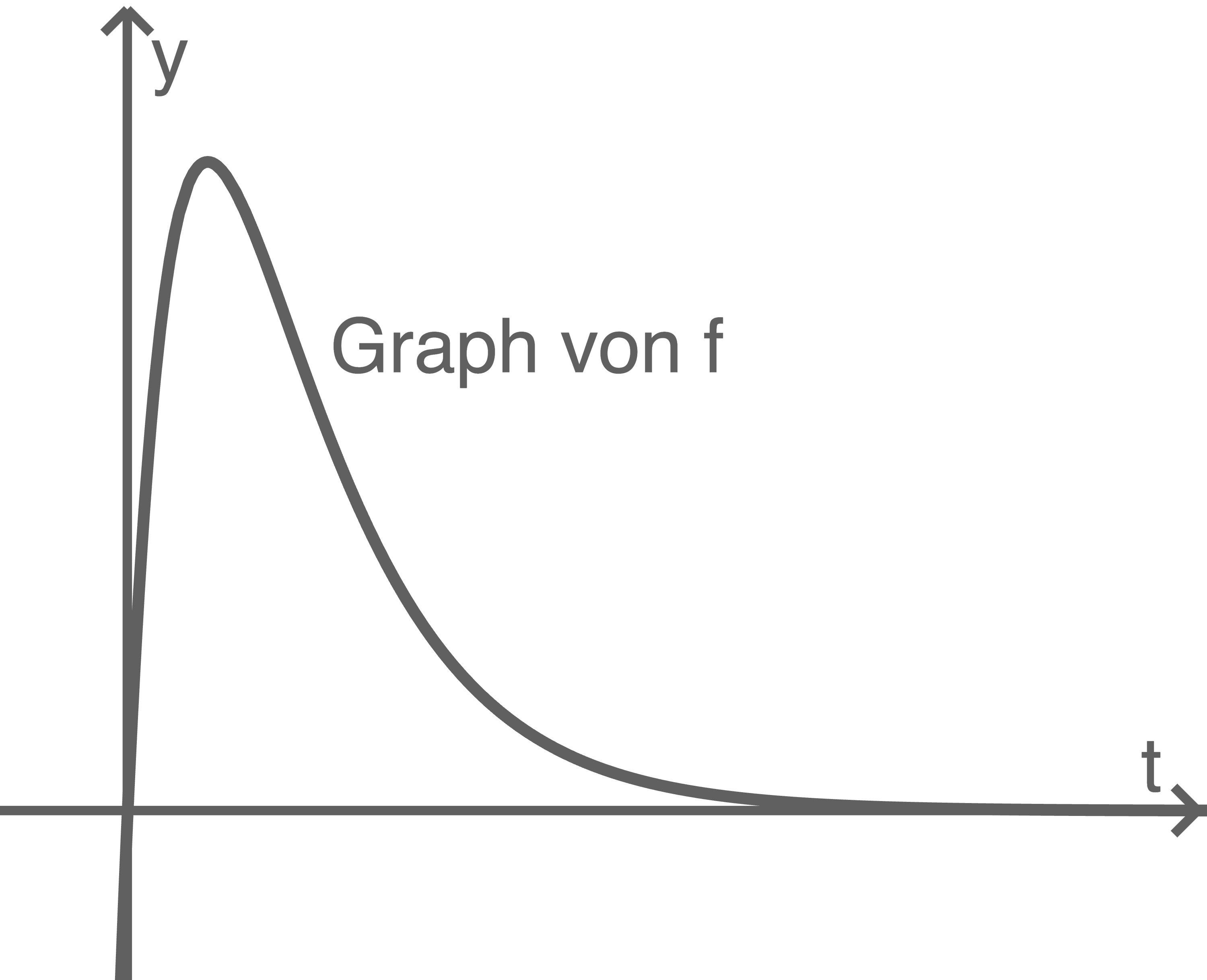
Abgebildet ist der Graph von
in Liter pro Sekunde).
Abgebildet ist der Graph von  Für die Ableitungsfunktion
Für die Ableitungsfunktion  von
von  gilt
gilt  .
.
a)
Weise nach, dass der maximale Atemfluss 7,5 Liter pro Sekunde beträgt.
(4 BE)
b)
Zeige, dass der Atemfluss zwei Sekunden nach Beginn des Ausatmens weniger als ein Prozent seines maximalen Werts beträgt.
(2 BE)
c)
Bestimme rechnerisch die Länge des Zeitraums, in dem der Atemfluss mindestens 5 Liter pro Sekunde beträgt.
(7 BE)
d)
Formuliere eine Fragestellung im Sachzusammenhang, die auf die Gleichung  führt.
führt.
(3 BE)
e)
Berechne 
(4 BE)
f)
Bei einer anderen Modellierung wird der Atemfluss ab dem Zeitpunkt  nicht mehr durch die Funktion
nicht mehr durch die Funktion  sondern durch die Gleichung der Tangente an den Graphen von
sondern durch die Gleichung der Tangente an den Graphen von  im Punkt
im Punkt  beschrieben.
Bei dieser Modellierung gibt es einen Zeitpunkt
beschrieben.
Bei dieser Modellierung gibt es einen Zeitpunkt  , zu dem der Atemfluss 0 Liter pro Sekunde beträgt.
Bestimme den Wert von
, zu dem der Atemfluss 0 Liter pro Sekunde beträgt.
Bestimme den Wert von 
(4 BE)
g)
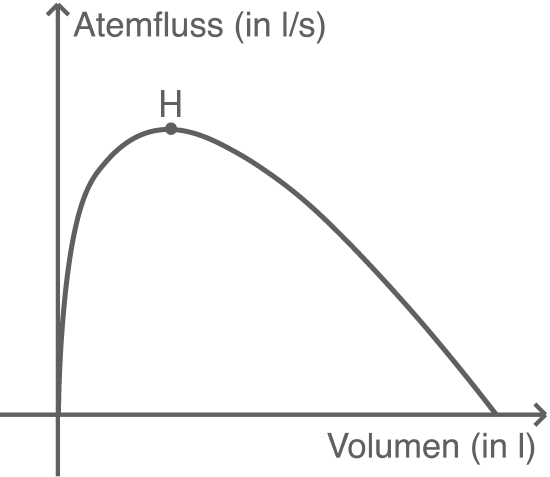
Bei ärztlichen Untersuchungen werden Atemfluss-Volumen-Diagramme betrachtet. Diese stellen den Atemfluss in Abhängigkeit vom Volumen der ausgeatmeten Luft dar.
Abgebildet ist das Diagramm zu derjenigen Messung, die durch die Funktion  beschrieben wird. Betrachtet wird der Hochpunkt
beschrieben wird. Betrachtet wird der Hochpunkt  der abgebildeten Kurve.
Begründe, dass
der abgebildeten Kurve.
Begründe, dass  der in a) genannte maximale Atemfluss ist, und gib einen Term an, mit dem
der in a) genannte maximale Atemfluss ist, und gib einen Term an, mit dem  berechnet werden kann.
berechnet werden kann.
(4 BE)
Aufgabe I 2.2
Für jedes a mit
a)
Weise nach, dass jede Funktion  streng monoton wachsend ist.
streng monoton wachsend ist.
(4 BE)
Die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  die Tangente an den Graphen der Umkehrfunktion
die Tangente an den Graphen der Umkehrfunktion  im Punkt
im Punkt  und die Koordinatenachsen schließen im 1. Quadranten des Koordinatensystems ein Viereck
und die Koordinatenachsen schließen im 1. Quadranten des Koordinatensystems ein Viereck  ein.
ein.
 ist der Schnittpunkt von
ist der Schnittpunkt von  mit der
mit der  -Achse.
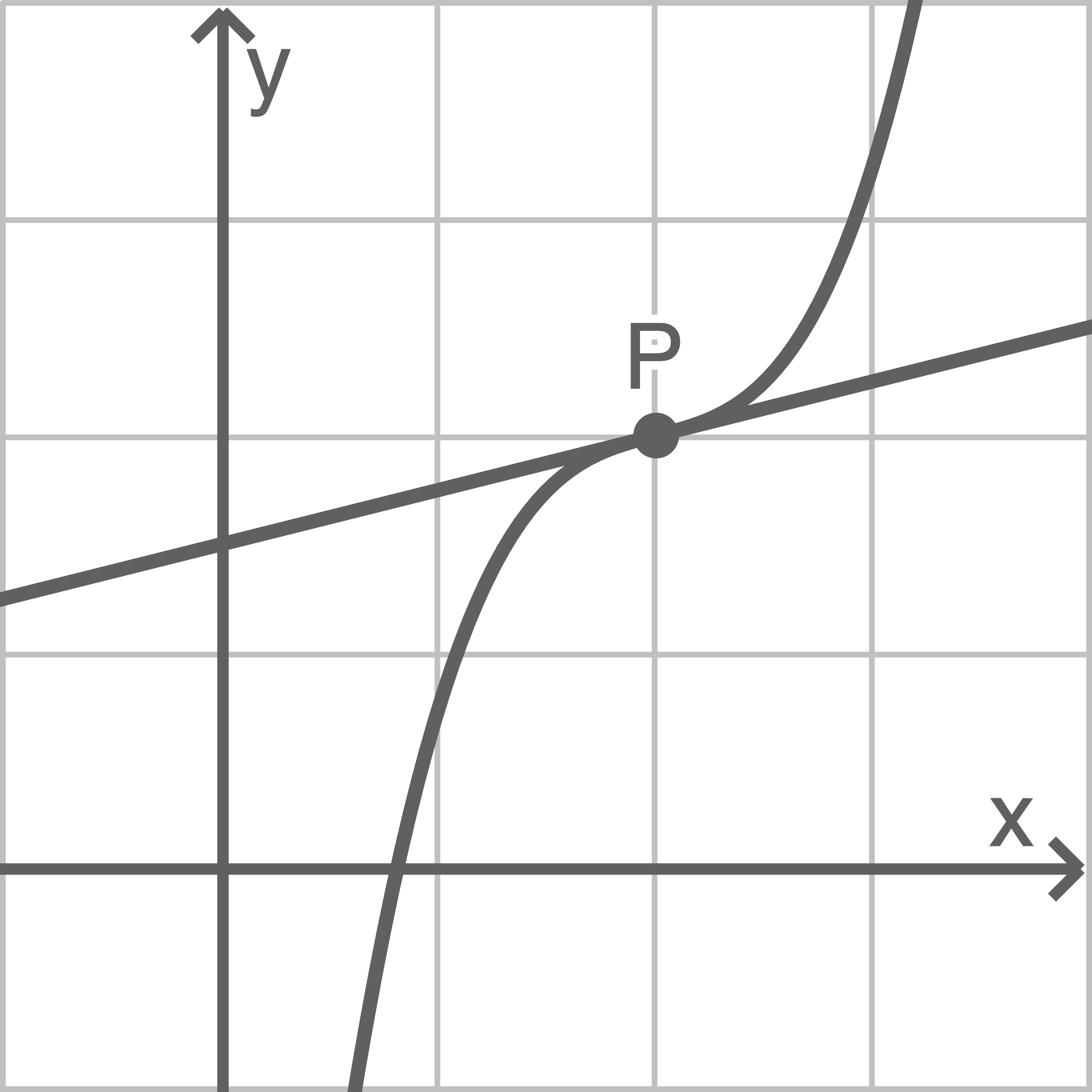
Abgebildet sind beispielhaft der Graph von
-Achse.
Abgebildet sind beispielhaft der Graph von  sowie die Tangente
sowie die Tangente 
b)
Begründe, dass der Punkt  zwischen dem Ursprung und dem Punkt
zwischen dem Ursprung und dem Punkt  liegt und dass der Flächeninhalt des Vierecks
liegt und dass der Flächeninhalt des Vierecks  kleiner als 4 ist.
kleiner als 4 ist.
(5 BE)
c)
Für einen Wert von  hat der Innenwinkel des Vierecks
hat der Innenwinkel des Vierecks  bei
bei  die Größe
die Größe  Begründe ohne Berechnung des Werts von
Begründe ohne Berechnung des Werts von  dass der Steigungswinkel der zugehörigen Tangente
dass der Steigungswinkel der zugehörigen Tangente  die Größe
die Größe  hat.
hat.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung I 1.1
a)
Für jeden Wert von  ist der Funktionsterm von
ist der Funktionsterm von  ein Polynom, welches nur ungerade Exponenten von
ein Polynom, welches nur ungerade Exponenten von  besitzt und somit symmetrisch zum Koordinatenursprung ist.
besitzt und somit symmetrisch zum Koordinatenursprung ist.
b)
1. Schritt: Ableitungen bestimmen
![\(\begin{array}[t]{rll}
f_{a;b}](https://mathjax.schullv.de/c6c88b3f8dd7154e2c625355dd2a39ae87aef694e9a3994b28c9047389aa7483?color=5a5a5a) 2. Schritt: Notwendige Bedingung für Extremstellen überprüfen
2. Schritt: Notwendige Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
f_{a;b}](https://mathjax.schullv.de/946cea5e380eb322da786e5b9529ad73b3ee2209430ed40a9067fcc8007ca792?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Wegen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Wegen  gilt:
gilt:
 Der Graph von
Der Graph von  besitzt somit einen Tiefpunkt mit der
besitzt somit einen Tiefpunkt mit der  -Koordinate
-Koordinate  Begründung
Da der Graph von
Begründung
Da der Graph von  punktsymmetrisch zum Ursprung ist, liegt an der Stelle
punktsymmetrisch zum Ursprung ist, liegt an der Stelle  ein Hochpunkt vor.
Wegen
ein Hochpunkt vor.
Wegen  gilt:
gilt:
 Somit besitzt der Hochpunkt immer eine kleinere
Somit besitzt der Hochpunkt immer eine kleinere  -Koordinate als der Tiefpunkt.
-Koordinate als der Tiefpunkt.
c)
Da die Funktion eine Nullstelle bei  hat, muss gelten:
hat, muss gelten:
![\(\begin{array}[t]{rll}
f_{a;b}(3)&=& 0 & \\[5pt]
a\cdot 3^3-b\cdot 3&=& 0 & \\[5pt]
27a-3b&=& 0 &\quad \scriptsize \mid\; +3b\\[5pt]
27a&=& 3b &\quad \scriptsize \mid\; :3\\[5pt]
9a&=& b
\end{array}\)](https://mathjax.schullv.de/2320fc888c0f19e6d56d3d66db9fd4899d923ded766ca63c0581ea1b85634efb?color=5a5a5a) Der Graph der Funktion verläuft für
Der Graph der Funktion verläuft für  im vierten Quadranten. Da die mit der
im vierten Quadranten. Da die mit der  -Achse eingeschlossene Fläche in diesem Intervall unterhalb der
-Achse eingeschlossene Fläche in diesem Intervall unterhalb der  -Achse verläuft, ist der orientierte Flächeninhalt negativ.
Es soll also gelten:
Die zugehörigen Werte der Parameter folgen also mit
-Achse verläuft, ist der orientierte Flächeninhalt negativ.
Es soll also gelten:
Die zugehörigen Werte der Parameter folgen also mit  und
und 
d)
1. Schritt: Tangentengleichung aufstellen
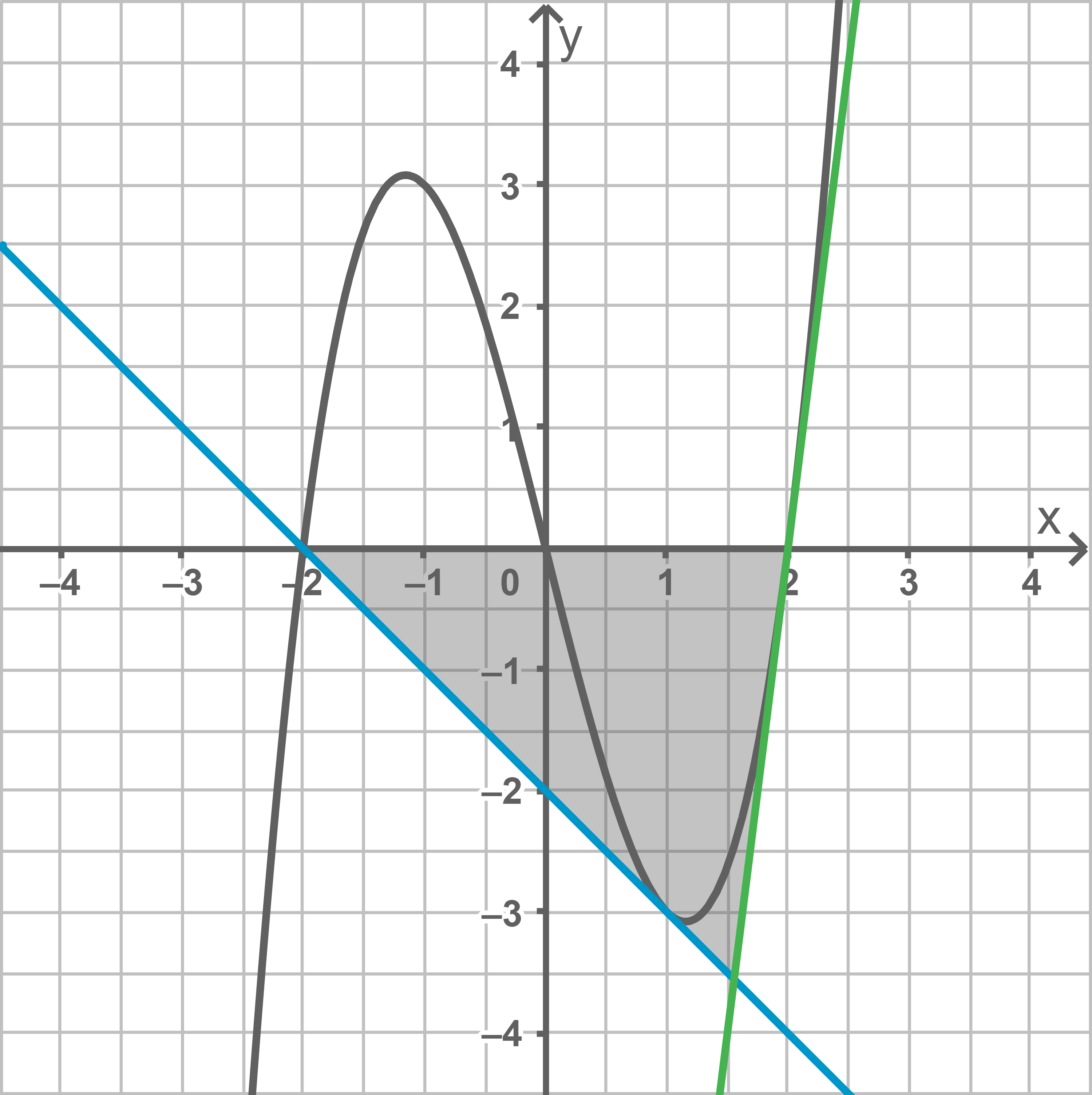 2. Schritt: Schnittpunkt berechnen
Gleichsetzen der Tangentengleichung und der Gleichung der Geraden
2. Schritt: Schnittpunkt berechnen
Gleichsetzen der Tangentengleichung und der Gleichung der Geraden  liefert:
liefert:
![\(\begin{array}[t]{rll}
8x-16&=& -x-2 &\quad \scriptsize \mid\;+16 \quad \scriptsize \mid\;+x \\[5pt]
9x&=&14 &\quad \scriptsize \mid\;:9\\[5pt]
x&=&\dfrac{14}{9}
\end{array}\)](https://mathjax.schullv.de/a92500e435d87739e96cd7ba1e823eacedfe80adb6a84d1b763c09317169a8de?color=5a5a5a) Einsetzen in
Einsetzen in  liefert:
liefert:
![\(\begin{array}[t]{rll}
y&=& -\dfrac{14}{9}-2 \\[5pt]
&=& -\dfrac{32}{9}
\end{array}\)](https://mathjax.schullv.de/fb9d21b574f2fe0ce0e9c03755aa88c6c504cade4df77e0e2ab9794772c3abfb?color=5a5a5a) Der Schnittpunkt besitzt somit die Koordinaten
Der Schnittpunkt besitzt somit die Koordinaten  3. Schritt: Flächeninhalt berechnen
Die Dreiecksseite, die auf der
3. Schritt: Flächeninhalt berechnen
Die Dreiecksseite, die auf der  -Achse liegt, entspricht der Grundseite des Dreiecks und besitzt eine Länge von
-Achse liegt, entspricht der Grundseite des Dreiecks und besitzt eine Länge von ![\(2-(-2)=4\;[\text{LE}].\)](https://mathjax.schullv.de/54f70aeafe69b6169d1c34c2fa843c0c7bf6907fc9dd2878f3083a2bffa14668?color=5a5a5a) Die
Die  -Koordinate des Schnittpunkts gibt die Höhe
-Koordinate des Schnittpunkts gibt die Höhe  des Dreiecks an.
Es gilt also:
des Dreiecks an.
Es gilt also:
![\(\begin{array}[t]{rll}
A&=&\dfrac{1}{2}\cdot 4\cdot \dfrac{32}{9} \\[5pt]
&=& \dfrac{64}{9}\\[5pt]
&\approx & 7,11 \;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/a10c0b9be3f39844a8dbdff802e813c80b12f35820feee2968aff2a88ad71ab7?color=5a5a5a)
Für die erste Ableitung von  gilt:
gilt:
 Für die Steigung
Für die Steigung  der in grün eingezeichneten Tangente im Punkt
der in grün eingezeichneten Tangente im Punkt  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/94580ed6c82dc7c212dc369faa7d3619363f84f4b309dec1ded2387ba89ea895?color=5a5a5a) Einsetzen von
Einsetzen von  und der Koordinaten von
und der Koordinaten von  in die allgemeine Tangentengleichung liefert:
in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
t: \quad y&=& m\cdot x+c& \\[5pt]
0&=& 8 \cdot 2+c&\quad \scriptsize \mid\; -16 \\[5pt]
-16&=& c
\end{array}\)](https://mathjax.schullv.de/7ed818e0302b17a1d99d4e8605627c6015e375f069010783032aeedefe3778d5?color=5a5a5a) Eine Gleichung der Tangente ist somit gegeben durch
Eine Gleichung der Tangente ist somit gegeben durch 

Hilfsskizze
e)
Für einen Punkt  auf dem Graphen von
auf dem Graphen von  mit den allgemeinen Koordinaten
mit den allgemeinen Koordinaten  besitzt der Mittelpunkt der Verbindungsstrecke von
besitzt der Mittelpunkt der Verbindungsstrecke von  mit dem Koordinatenursprung die Koordinaten
mit dem Koordinatenursprung die Koordinaten  Gleichsetzen von
Gleichsetzen von  mit
mit  liefert:
liefert:
![\(\begin{array}[t]{rll}
h\left(\dfrac{x}{2}\right)&=&\dfrac{f(x)}{2} \\[5pt]
4\cdot\left(\dfrac{x}{2}\right)^3-4\cdot\dfrac{x}{2}&=&\dfrac{x^3-4x}{2} \\[5pt]
\dfrac{1}{2}x^3-2x&=&\dfrac{1}{2}x^3-2x
\end{array}\)](https://mathjax.schullv.de/66ed057f01ce23231cf072235014c24b4c8cd6c106c2943e311ad742648f411a?color=5a5a5a) Da die beiden Seiten der Gleichung übereinstimmen, ist die Aussage folglich richtig.
Da die beiden Seiten der Gleichung übereinstimmen, ist die Aussage folglich richtig.
Lösung I 1.2
a)
Die zeitliche Differenz zwischen 8:30 Uhr und 10:00 Uhr beträgt 1,5 Stunden.
Für die im Mittel pro Stunde eingegangenen Lesebestätigungen in diesem Zeitfenster folgt somit:

b)
Wert berechnen
![\(\begin{array}[t]{rll}
k(2)&=&u(2) \\[5pt]
&=&100\cdot2^3-900\cdot2^2+2300\cdot2 \\[5pt]
&=&1800
\end{array}\)](https://mathjax.schullv.de/cf14da138b89b67ed02efd37db65bd15ebc7dd044e281d8226c7eb9abf90bbab?color=5a5a5a) Ergebnis interpretieren
Nach dem Modell beträgt die momentane Änderungsrate der Anzahl der seit 7:00 Uhr eingegangenen Lesebestätigungen um 9:00 Uhr
Ergebnis interpretieren
Nach dem Modell beträgt die momentane Änderungsrate der Anzahl der seit 7:00 Uhr eingegangenen Lesebestätigungen um 9:00 Uhr 
c)
Aus dem Funktionsterm von  können die Nullstellen bei
können die Nullstellen bei  und
und  abgelesen werden. An der Stelle
abgelesen werden. An der Stelle  liegt folglich ein Vorzeichenwechsel von plus nach minus vor.
Somit würden die Änderungsraten nach 15:00 Uhr negative Werte annehmen, was im Sachzusammenhang keinen Sinn ergibt.
liegt folglich ein Vorzeichenwechsel von plus nach minus vor.
Somit würden die Änderungsraten nach 15:00 Uhr negative Werte annehmen, was im Sachzusammenhang keinen Sinn ergibt.
d)
Anzahl der Lesebestätigungen berechnen
10:00 Uhr entspricht 3 Stunden nach 7:00 Uhr und 15:00 Uhr entspricht analog 8 Stunden.
Es gilt also:
Prozentuale Abweichung ermitteln
Mit den Werten aus der Tabelle folgt für die gesuchte prozentuale Abweichung:

Lösung I 2.1
a)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/f156d3b1dc49bc93999b9d4e18bbcfd0e3e0f52041c84ee912d40c149bfa15cc?color=5a5a5a) Wegen
Wegen  folgt mit dem Satz vom Nullprodukt:
folgt mit dem Satz vom Nullprodukt:
![\(\begin{array}[t]{rll}
1-2\mathrm e^{-3\cdot t}&=& 0&\quad \scriptsize \mid\; +2\mathrm e^{-3 t} \\[5pt]
1&=& 2\mathrm e^{-3t}&\quad \scriptsize \mid\; :2 \\[5pt]
\dfrac{1}{2}&=& \mathrm e^{-3t}&\quad \scriptsize \mid\; \ln(\,) \\[5pt]
\ln\left(\dfrac{1}{2}\right)&=& -3t& \\[5pt]
-\ln(2)&=& -3t&\quad \scriptsize \mid\; :(-3) \\[5pt]
\dfrac{\ln(2)}{3}&=& t
\end{array}\)](https://mathjax.schullv.de/4cbfaa8e7d4b31de12f4b6b441fc883a757459cb7598437da008366061f8b2b3?color=5a5a5a) Da aus der Abbildung hervorgeht, dass genau ein Hochpunkt existiert, ist das Überprüfen der hinreichenden Bedingung nicht notwendig.
2. Schritt:
Da aus der Abbildung hervorgeht, dass genau ein Hochpunkt existiert, ist das Überprüfen der hinreichenden Bedingung nicht notwendig.
2. Schritt:  -Koordinate berechnen
-Koordinate berechnen
![\(\begin{array}[t]{rll}
f\left(\dfrac{\ln(2)}{3}\right)&=& 30 \cdot \left( \mathrm{e}^{-3 \cdot \frac{\ln(2)}{3}} - \mathrm{e}^{-6 \cdot \frac{\ln(2)}{3}} \right)& \\[5pt]
&=& 30 \cdot \left( \mathrm{e}^{-\ln(2)} - \mathrm{e}^{-2 \ln(2)} \right)& \\[5pt]
&=& 30 \cdot \left( \dfrac{1}{2} - \dfrac{1}{4} \right) & \\[5pt]
&=& 30 \cdot \dfrac{1}{4}& \\[5pt]
&=& 7,5 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c3588cce83a32ebaa2ae39d23ef1ec30850b0245282a7a88d3309adee48651b8?color=5a5a5a) Somit beträgt der maximale Atemfluss 7,5 Liter pro Sekunde.
Somit beträgt der maximale Atemfluss 7,5 Liter pro Sekunde.
b)
Zwei Sekunden nach Beginn des Ausatmens gilt:
![\(\begin{array}[t]{rll}
f(2)&=& 30\cdot (\mathrm e^{-3\cdot 2}-\mathrm e^{-6\cdot 2}) &\\[5pt]
&=& 30 \cdot (\mathrm e^{-6}-\mathrm e^{-12})&\\[5pt]
&\approx & 0,074
\end{array}\)](https://mathjax.schullv.de/57a913b90d80efef19efa7fd5a7b53486dc43ac156714887b05cc0f002b36077?color=5a5a5a) Ein Prozent des maximalen Werts entspricht
Ein Prozent des maximalen Werts entspricht  Liter pro Sekunde.
Zwei Sekunden nach Beginn des Ausatmens beträgt der Atemfluss folglich weniger als ein Prozent seines maximalen Werts.
Liter pro Sekunde.
Zwei Sekunden nach Beginn des Ausatmens beträgt der Atemfluss folglich weniger als ein Prozent seines maximalen Werts.
c)
Zu den Zeitpunkten, an denen der Atemfluss genau 5 Liter pro Sekunde beträgt, gilt:
![\(\begin{array}[t]{rll}
f(t)&=& 5 &\\[5pt]
30\cdot (\mathrm e^{-3t}-\mathrm e^{-6t})&=& 5 &\quad \scriptsize \mid\; :30 \\[5pt]
\mathrm e^{-3t}-\mathrm e^{-6t}&=& \dfrac{1}{6} & \\[5pt]
\mathrm e^{-3t}-\left(\mathrm e^{-3t}\right)^2&=& \dfrac{1}{6} &\quad \scriptsize \mid\; - \dfrac{1}{6} \\[5pt]
- \left(\mathrm e^{-3t}\right)^2+ \mathrm e^{-3t}- \dfrac{1}{6} &=& 0 &\quad \scriptsize \mid\; \cdot (-1) \\[5pt]
\left(\mathrm e^{-3t}\right)^2- \mathrm e^{-3t}+ \dfrac{1}{6} &=& 0
\end{array}\)](https://mathjax.schullv.de/3665554329d74858b1545de12e47e3651f59ec4db44543905e1bf97585539b60?color=5a5a5a) Substitution mit
Substitution mit  ergibt:
ergibt:

![\(\begin{array}[t]{rll}
x_1&=& \mathrm e^{-3t_1} & \\[5pt]
0,789&=& \mathrm e^{-3t_1} &\quad \scriptsize \mid\; \ln(\,) \\[5pt]
\ln(0,789) &=& -3t_1 & \quad \scriptsize \mid\;:(-3) \\[5pt]
\dfrac{\ln(0,789)}{-3} &=& t_1 \\[5pt]
0,079&\approx& t_1
\end{array}\)](https://mathjax.schullv.de/e9fe379962fab4bb3d5fcddd916b52c674578e2de2f3d61ce762d9f2eec80791?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_2&=& \mathrm e^{-3t_2} & \\[5pt]
0,211&=& \mathrm e^{-3t_2} &\quad \scriptsize \mid\; \ln(\,) \\[5pt]
\ln(0,211) &=& -3t_2 & \quad \scriptsize \mid\;:(-3) \\[5pt]
\dfrac{\ln(0,211)}{-3} &=& t_2 \\[5pt]
0,519&\approx& t_2
\end{array}\)](https://mathjax.schullv.de/1561d8dbd9c780595e28466b6722ade339a896fa4128db448bd6f65e8cbd0c71?color=5a5a5a) Die Länge des Zeitraums, in dem der Atemfluss mindestens 5 Liter pro Sekunde beträgt, beträgt somit
Die Länge des Zeitraums, in dem der Atemfluss mindestens 5 Liter pro Sekunde beträgt, beträgt somit  Sekunden.
Sekunden.
Mit der abc-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1;2}&=& \dfrac{-(-1) \pm \sqrt{(-1)^2-4\cdot 1\cdot \dfrac{1}{6}}}{2\cdot 1} \\[5pt]
x_{1;2}&=& \dfrac{1\pm\sqrt{\dfrac{1}{3}}}{2}&\\[5pt]
x_1&\approx& 0,789&\\[5pt]
x_2&\approx& 0,211&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/6843751cb50211aa336badad019fa8dae830651b79a69b2bfd9761c0525da816?color=5a5a5a)
Alternativ ergibt sich mit der pq-Formel:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{(-1)}{2} \pm \sqrt{\left(\dfrac{(-1)}{2}\right)^2-\dfrac{1}{6}} \\[5pt]
x_{1;2}&=& \dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}-\dfrac{1}{6}}&\\[5pt]
x_1&=& 0,789 &\\[5pt]
x_2&=& 0,211&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/ade44d8bd87ca95551ad00b03b1275fef11a6e7fc00056ee54fa6847ecc2f7f5?color=5a5a5a)
Rücksubstitution liefert nun:
d)
Zu welchem Zeitpunkt beträgt das Volumen der ausgeatmeten Luft ein Viertel des Volumens der während der ersten zwei Sekunden ausgeatmeten Luft?
e)
f)
1. Schritt: Tangentengleichung aufstellen
 -Koordinate berechnen:
-Koordinate berechnen:
![\(\begin{array}[t]{rll}
f(1,5)&=& 30 \cdot\left(\mathrm{e}^{-3\cdot 1,5}-\mathrm{e}^{-6 \cdot 1,5}\right) & \\[5pt]
&\approx& 0,33
\end{array}\)](https://mathjax.schullv.de/819615da16c83552a94122ffbf128b5507809676133ce076a9dde471805949fb?color=5a5a5a) Für die Steigung
Für die Steigung  der Tangente gilt:
der Tangente gilt:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/3cfc1a1c83f35c1054961daf845c4f4cda10ad7cf7a70f762bdfdd1f39551692?color=5a5a5a) Einsetzen in die allgemeine Tangentengleichung liefert:
Einsetzen in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
y&=& m\cdot t+c&\\[5pt]
0,33&=& -0,98 \cdot 1,5+c&\\[5pt]
0,33&=& -1,47 +c& \quad \scriptsize \mid +1,47 \\[5pt]
1,8&=& c
\end{array}\)](https://mathjax.schullv.de/7867ea042a8b22e60baa90dbfcd5555f4ffcdd67be45d58011ec66dac91e8eb5?color=5a5a5a) Eine Gleichung der Tangente ist somit gegeben durch
Eine Gleichung der Tangente ist somit gegeben durch  2. Schritt: Zeitpunkt berechnen
Zu dem Zeitpunkt, an dem der Atemfluss 0 Liter pro Sekunde beträgt, gilt:
2. Schritt: Zeitpunkt berechnen
Zu dem Zeitpunkt, an dem der Atemfluss 0 Liter pro Sekunde beträgt, gilt:
![\(\begin{array}[t]{rll}
0&=& -0,98t+1,8&\quad \scriptsize \mid\; -1,8 \\[5pt]
-1,8&=& -0,98t&\quad \scriptsize \mid\; :(-0,98)\\[5pt]
1,84&\approx& t
\end{array}\)](https://mathjax.schullv.de/2c6b1b5b6e0049434aac931764a697156b25e6da6145021e81c482abf13f3ab2?color=5a5a5a) Der Wert von
Der Wert von  folgt also mit
folgt also mit 
g)
Begründung
Der maximale Atemfluss beträgt 7,5 Liter pro Sekunde, unabhängig davon, ob der Atemfluss in Abhängigkeit von der Zeit oder vom ausgeatmeten Volumen dargestellt wird.
Term angeben

Lösung I 2.2
a)
Ableitung bestimmen:
![\(\begin{array}[t]{rll}
f_a(x)&=& (x-2)^3+a(x-2)+2& \\[5pt]
&=& (x-2)^3+ax-2a+2& \\[5pt]
f](https://mathjax.schullv.de/ac6554e5dbd85c525f30fa51210ed497e85423da19f98072663c2f1f33fdc3c3?color=5a5a5a) Aufgrund des geraden Exponenten gilt
Aufgrund des geraden Exponenten gilt  Mit
Mit  folgt direkt
folgt direkt  Somit ist jede Funktion
Somit ist jede Funktion  streng monoton wachsend.
streng monoton wachsend.
b)
Lage des Punkts begründen
Für die Steigung  der Tangente
der Tangente  gilt:
gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/45bfe2e8b2fd7470e917c70c058cc9a26322082e0910e4272498f96b4f7ae592?color=5a5a5a) Die
Die  -Achse hat einen Abstand von zwei Längeneinheiten in negative
-Achse hat einen Abstand von zwei Längeneinheiten in negative  -Richtung zum Punkt
-Richtung zum Punkt  Der Schnittpunkt von
Der Schnittpunkt von  mit der
mit der  -Achse besitzt somit die
-Achse besitzt somit die  -Koordinate
-Koordinate  Wegen
Wegen  gilt für die
gilt für die  -Koordinate des Schnittpunkts:
-Koordinate des Schnittpunkts:

 liegt folglich oberhalb des Ursprungs und unterhalb des Punkts
liegt folglich oberhalb des Ursprungs und unterhalb des Punkts  Flächeninhalt begründen
Aus Symmetriegründen schneidet die Tangente an den Graphen von
Flächeninhalt begründen
Aus Symmetriegründen schneidet die Tangente an den Graphen von  die
die  -Achse zwischen dem Ursprung und dem Punkt
-Achse zwischen dem Ursprung und dem Punkt  Mit den Punkten
Mit den Punkten  und
und  besitzt das Quadrat
besitzt das Quadrat  einen Flächeninhalt von 4 Flächeneinheiten.
Da die Tangenten die Koordinatenachsen zwischen den Werten 0 und 2 schneiden, liegt das Viereck
einen Flächeninhalt von 4 Flächeneinheiten.
Da die Tangenten die Koordinatenachsen zwischen den Werten 0 und 2 schneiden, liegt das Viereck  innerhalb des Quadrats
innerhalb des Quadrats  und besitzt somit einen kleineren Flächeninhalt als 4.
und besitzt somit einen kleineren Flächeninhalt als 4.
c)
Die Innenwinkelsumme eines Vierecks beträgt  Aus Symmetriegründen gilt für den Winkel
Aus Symmetriegründen gilt für den Winkel  im Eckpunkt
im Eckpunkt 
 Daraus folgt die Größe des Steigungswinkels der Tangente
Daraus folgt die Größe des Steigungswinkels der Tangente  mit
mit 
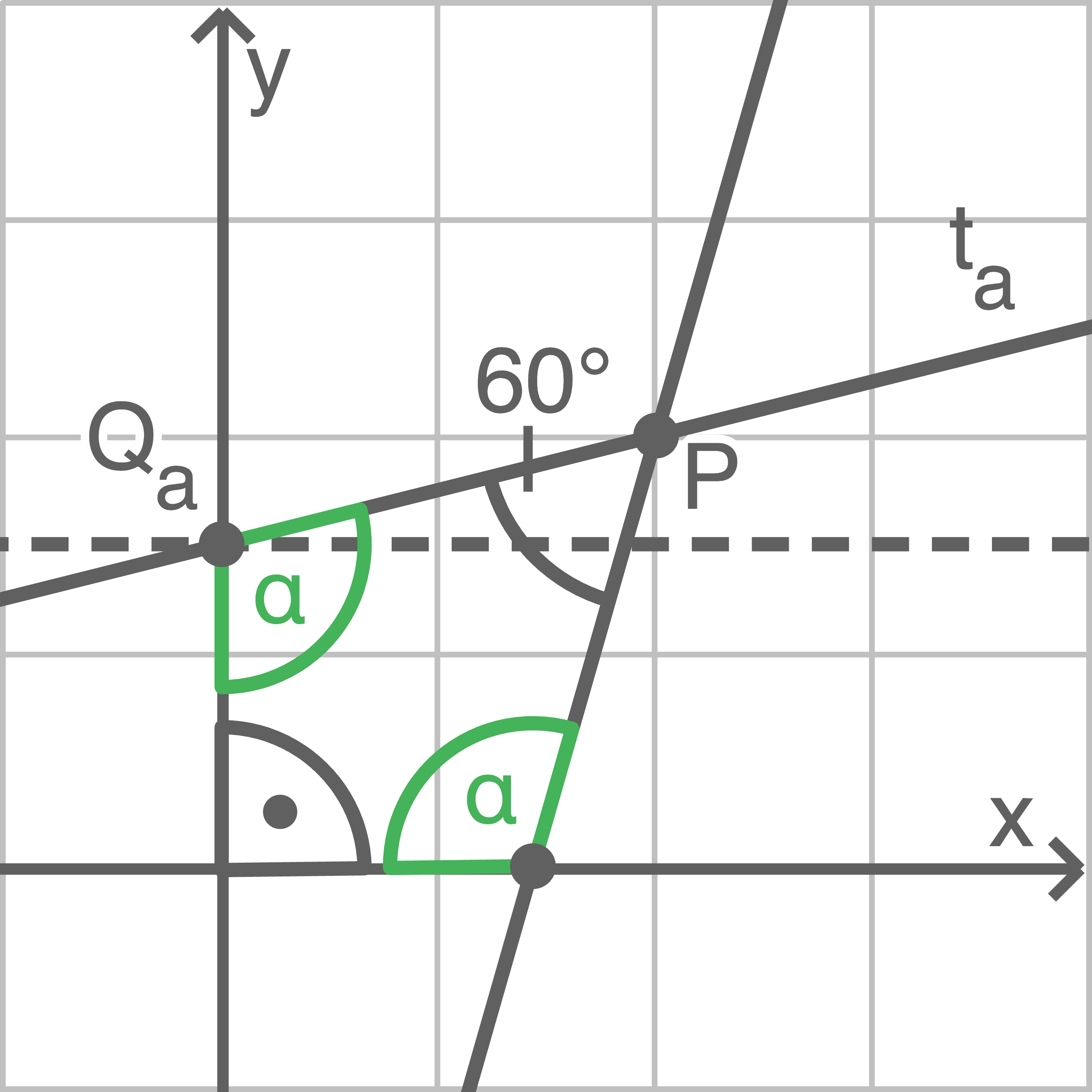
Hilfsskizze