Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=\sqrt{x}\cdot \sin\left(x^2 \right).$

(2 VP)

Aufgabe 2

Untersuche, ob der Wert des Integrals $\displaystyle\int_{3}^{\mathrm e+2}\dfrac{1}{x-2}\;\mathrm dx$ ganzzahlig ist.

(2,5 VP)

Aufgabe 3

Gegeben ist die Funktion $f$ mit $f(x)=4x^2-4x+5.$ $F$ ist eine Stammfunktion von $f.$
Bestimme die Stelle, an der die Graphen von $F$ und $f$ parallele Tangenten besitzen.

(2,5 VP)

Aufgabe 4

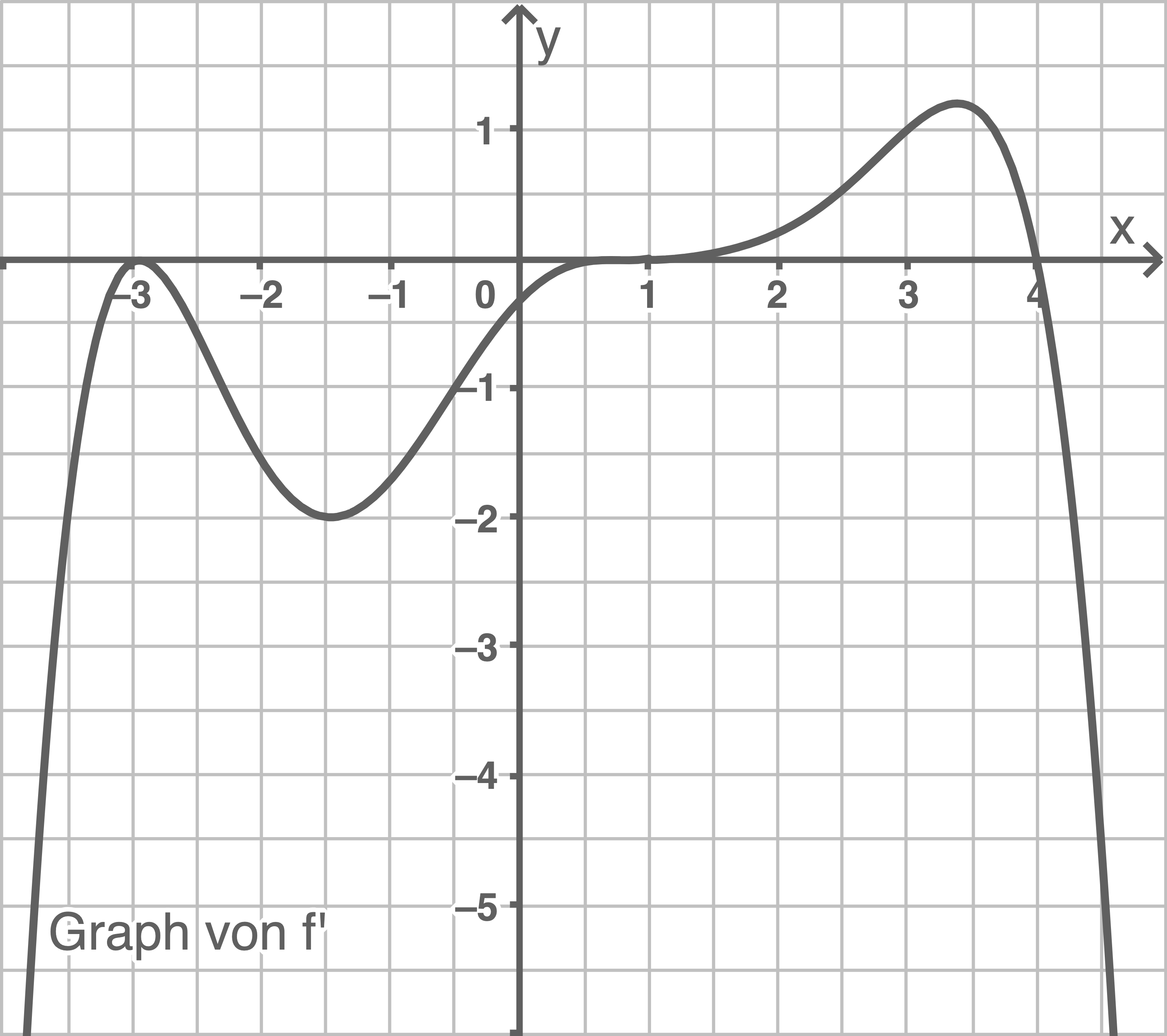
Die Abbildung zeigt den Graphen der Ableitungsfunktion $\( f$ einer ganzrationalen Funktion $f.$
Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Antwort.

(1)

Im Bereich $-3,5\leq x\leq 4,5$ besitzt $f$ genau drei Extremstellen.

(2)

Die Gleichung $\( f$ hat im abgebildeten Bereich genau zwei Lösungen.

(3)

Die Funktion $\( f$ hat an der Stelle $x=-3$ einen Vorzeichenwechsel von positiven zu negativen Werten.

Graph von f' auf einem Koordinatensystem mit Achsenbeschriftungen.

(3 VP)

Aufgabe 5

Gegeben sind die Ebene $E:2x_1+2x_2+x_3=5$ und die Gerade $g:\overrightarrow{x}=\pmatrix{1\\b\\1} + s\cdot \pmatrix{1\\0\\a}.$
Die Gerade $g$ liegt in $E.$

Bestimme die Werte für $a$ und $b.$

Gib eine Gleichung einer Geraden $h$ an, die ebenfalls in $E$ liegt, und senkrecht zur Geraden $g$ verläuft.

(3,5 VP)

Aufgabe 6

Gegeben ist die Ebene $E:x_1+2x_2-x_3 = 4.$

Begründe, dass die Spurpunkte von $E$ die Ecken eines gleichschenkligen Dreiecks bilden.

Die Ebene $F:\overrightarrow{x}=\pmatrix{-2\\-2\\0}+r\cdot\pmatrix{2\\3\\8}$ $+s\cdot \pmatrix{1\\2\\0}$ schneidet die Ebene $E.$ Bestimme eine Gleichung der Schnittgeraden.

(3,5 VP)

Aufgabe 7

Zwei ideale Würfel werden gleichzeitig geworfen.

Bestimme die Wahrscheinlichkeit dafür, dass zwei verschiedene Augenzahlen fallen.

Mit welcher Wahrscheinlichkeit erhält man eine "1" und eine "2"?

Mit welcher Wahrscheinlichkeit zeigen die Würfel zwei aufeinanderfolgende Zahlen?

(3 VP)

Lösung 1

Mit der Produkt- und der Kettenregel folgt:

$\(f$

Lösung 2

$\displaystyle\int_{3}^{\mathrm e +2}\dfrac{1}{x-2}\;\mathrm dx= \left[\ln \left(x-2\right) \right]_3^{\mathrm e+2}$ $=\ln \left(\mathrm e+2-2\right)-\ln \left(3-2\right)$ $= \ln \left(\mathrm e\right)-\ln \left(1\right) =1-0= 1$

Der Wert des Integrals ist also ganzzahlig.

Lösung 3

Die Graphen von $F$ und $f$ besitzen an den Stellen parallele Tangenten, an denen ihre Steigungen identisch sind. Diese wird jeweils durch die erste Ableitungsfunktion beschrieben. Also sind die Stellen $x$ gesucht mit $\( f(x)=f$

$\( f$

Gleichsetzen liefert:

$\( \begin{array}[t]{rll} f(x)&=& f$

An der Stelle $x=1,5$ haben die Graphen von $f$ und $F$ parallele Tangenten.

Lösung 4

(1)

$f$ besitzt an den Stellen Extremstellen, an denen $\(f$ Nullstellen mit Vorzeichenwechsel hat. Da $\( f$ nur in zwei der drei Nullstellen im angegebenen Bereich das Vorzeichen wechselt, besitzt $f$ nur zwei Extremstellen im angegebenen Bereich.
Die Aussage ist also falsch.

(2)

Zeichnet man die Gerade mit der Gleichung $y = -\frac{1}{2}x$ in die Abbildunng ein, so erhält man genau zwei Schnittpunkte mit dem Graphen von $\( f$
Die Aussage ist also wahr.

(3)

Der Graph von $\( f$ besitzt an der Stelle $x=-3$ einen Hochpunkt. An dieser Stelle wechselt also die Steigung von positiv zu negativ. Da die Steigung des Graphen von $\( f$ durch $\( f$ beschrieben wird, muss also $\( f$ in dieser Stelle das Vorzeichen von positiv zu negativ wechseln.
Die Aussage ist also wahr.

Lösung 5

Damit $g$ in $E$ liegt, muss der Stützvektor von $g$ in $E$ liegen und der Richtungsvektor senkrecht zum Normalenvektor von $E$ sein.

Einsetzen der Koordinaten des Stützpunkts in die Ebenengleichung liefert:

$\begin{array}[t]{rll} 2\cdot 1 +2\cdot b +1\cdot 1 &=& 5 \\[5pt] 3+2b&=& 5 \quad \scriptsize \mid\;-3 \\[5pt] 2b&=& 2 \quad \scriptsize \mid\; :2 \\[5pt] b&=& 1 \end{array}$

Das Skalarprodukt von Richtungsvektor und Normalenvektor muss Null betragen:

$\begin{array}[t]{rll} \pmatrix{2\\2\\1}\circ \pmatrix{1\\0\\a}&=& 0 \\[5pt] 2\cdot 1 +2\cdot 0 + 1\cdot a&=& 0 \\[5pt] 2+a &=& 0 \quad \scriptsize \mid\; -2 \\[5pt] a&=& -2 \end{array}$

Als Stützpunkt für $h$ kann der von $g$ verwendet werden. Der Richtungsvektor $\pmatrix{x\\y\\z}$ muss sowohl zum Richtungsvektor von $g$ als auch zum Normalenvektor von $E$ senkrecht stehen.
Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}&\pmatrix{x\\y\\z}\circ \pmatrix{1\\0\\-2}&=&0 \\[5pt] &x-2z&=&0 \\[5pt] &x&=& 2z \\[10pt] \text{II}&\pmatrix{x\\y\\z}\circ \pmatrix{2\\2\\1}&=&0 \\[5pt] &2x+2y+z&=&0 \end{array}$

$\text{I}$ in $\text{II}$ eingesetzt und eine der beiden Variablen festgesetzt, beispielsweise $y=1$ , ergibt:

$\begin{array}[t]{rll} 2x+2y+z &=&0\quad \scriptsize \mid\; y=1 \\[5pt] 2x+2+z &=&0\quad \scriptsize \mid\; x=2z \\[5pt] 2\cdot 2z + 2 + z&=&0 \\[5pt] 5z +2&=&0 \quad \scriptsize \mid\; -2\\[5pt] 5z&=&-2 \quad \scriptsize \mid\; :5\\[5pt] z&=& -\dfrac{2}{5} \end{array}$

$z= -\dfrac{2}{5}$ in $\text{I}$ eingesetzt ergibt $x=-\frac{4}{5}.$

Eine mögliche Geradengleichung ist also beispielsweise:

$h:\overrightarrow{x} = \pmatrix{1\\1\\1}+ t\cdot \pmatrix{-\frac{4}{5} \\ 1\\ - \frac{2}{5}}.$

Lösung 6

$\begin{array}[t]{rll} x_1+2\cdot 0 -0&=& 4 \\[5pt] x_1 &=& 4 \\[5pt] \end{array}$

Der erste Spurpunkt ist $S_1(4\mid 0\mid 0).$

$\begin{array}[t]{rll} 0+2\cdot x_2 -0&=& 4 \\[5pt] 2\cdot x_2 &=& 4 \\[5pt] x_2 &=& 2 \end{array}$

Der zweite Spurpunkt ist $S_2(0\mid 2\mid 0).$

$\begin{array}[t]{rll} 0+2\cdot 0 -x_3&=& 4 \\[5pt] -x_3 &=& 4 \\[5pt] x_3 &=& -4 \\[5pt] \end{array}$

Der dritte Spurpunkt ist $S_3(0 \mid 0 \mid -4).$

Den Koordinaten der drei Punkte kann man direkt entnehmen, dass $S_1$ und $S_3$ den gleichen Abstand zum Punkt $S_2$ haben. Die drei Punkte bilden also ein gleichschenkliges Dreieck.

$F$ eingesetzt in die Ebenengleichung von $E:x_1+2x_2-x_3=4$ liefert:

Rechenweg anzeigen

$s=2$

Einsetzen in die Ebenengleichung von $F$ liefert eine Gleichung der Schnittgerade:

$s: \overrightarrow{x}= \pmatrix{-2\\-2\\0} + r\cdot \pmatrix{2\\3\\8} + 2\cdot \pmatrix{1\\2\\0}\,$ $=\pmatrix{0\\2\\0} + r\cdot \pmatrix{2\\3\\8}$

Lösung 7

Wahrscheinlichkeit bestimmen

$P(\text{„Zwei verschiedene Augenzahlen“})$ $= 1- P(\text{„Zwei gleiche Augenzahlen“})$ $= 1- 6\cdot \frac{1}{6}\cdot \frac{1}{6}=\frac{5}{6}$

Wahrscheinlichkeit bestimmen

Zeigt der erste Würfel eine der beiden Zahlen an, muss der zweite die andere anzeigen. Also ergibt sich mit der Pfadmultiplikationsregel:

$P(\text{„1 und 2“})= \dfrac{2}{6}\cdot \dfrac{1}{6}$ $= \dfrac{1}{18}$

Mit einer Wahrscheinlichkeit von $\dfrac{1}{18}$ erhält man eine „1“ und eine „2“.

Wahrscheinlichkeit bestimmen

Es gibt $10$ Paare aufeinanderfolgender Zahlen. Diese haben jeweils die Wahrscheinlichkeit $\frac{1}{6}\cdot \frac{1}{6} = \frac{1}{36}.$ Mit der Pfadadditionsregel folgt:

$P(\text{„Aufeinanderfolgende Zahlen“})$ $=10\cdot \dfrac{1}{36}=\dfrac{10}{36} = \dfrac{5}{18}$

Mit einer Wahrscheinlichkeit von $\frac{5}{18}$ fallen zwei aufeinanderfolgende Zahlen.