Wahlteil B2

Aufgabe B2.1

Die Punkte $A(0\mid-6\mid0)$ , $B(6\mid0\mid0)$ , $C(0\mid6\mid0)$ und $S(0\mid 0\mid5)$ sind die Eckpunkte der Pyramide $ABCS$ . Der Punkt $M_1$ ist der Mittelpunkt der Kante $AS$ und $M_2$ ist der Mittelpunkt der Kante $CS$ . Die Ebene $E$ verläuft durch $M_1$ , $M_2$ und $B$ .

Die Ebene $E$ schneidet die Pyramide in einer Schnittfläche.
Stelle Pyramide und Schnittfläche in einem Koordinatensystem dar.
Berechne den Umfang der Schnittfläche.
Bestimme eine Koordinatengleichung von $E$ .
(Teilergebnis: $E: 5x_1 + 12x_3 = 30$ )

(4 VP)

Der Punkt $Q$ liegt auf der Kante $BS$ und bildet mit $M_1$ und $M_2$ ein rechtwinkliges Dreieck.
Bestimme die Koordinaten des Punktes $Q$ .

(3 VP)

Der Punkt $Z$ liegt in der $x_1x_3$ -Ebene und im Innern der Pyramide $ABCS$ .
Er hat von der Grundfläche $ABC,$ der Seitenfläche $ACS$ und von $E$ den gleichen Abstand.
Bestimme die Koordinaten von $Z.$

(3 VP)

Aufgabe B2.2

Eine Tanzgruppe besteht aus $8$ Anfängerpaaren und $4$ Fortgeschrittenenpaaren. Aus der Erfahrung vergangener Jahre weiß man, dass Anfängerpaare mit einer Wahrscheinlichkeit von $90$ $\%$ bei den abendlichen Tanzstunden anwesend sind, Fortgeschrittenenpaare mit einer Wahrscheinlichkeit von $75$ $\%$ . Man geht davon aus, dass die Entscheidungen der Tanzpaare über die Teilnahme an der Tanzstunde voneinander unabhängig sind.

Bestimme die Wahrscheinlichkeit dafür, dass an einem Abend alle Fortgeschrittenenpaare anwesend sind.
Bestimme die Wahrscheinlichkeit dafür, dass an einem Abend mindestens $6$ Anfängerpaare und höchstens $3$ Fortgeschrittenenpaare anwesend sind.
Wie groß ist die Wahrscheinlichkeit dafür, dass an einem Abend mindestens $11$ Paare anwesend sind?

(5 VP)

Aufgabe 2.1.

$\blacktriangleright$ Darstellung der Pyramide und der Schnittfläche im Koordinatensystem

Der Aufgabenstellung kannst du entnehmen, dass das Dreieck $ABC$ die Grundfläche der Pyramide mit Spitze $S(0\mid 0 \mid 5)$ ist. Weiterhin weißt du, dass die Ebene $E$ durch die Punkte $M_1$ , $M_2$ und $B$ verläuft. Dabei ist $M_1$ der Mittelpunkt der Kante $AS$ und $M_2$ der Mittelpunkt der Kante $CS$ . Du sollst die Pyramide zusammen mit der Schnittfläche von Pyramide und Ebene darstellen. Dazu musst du zuerst die Koordinaten von $M_1$ und $M_2$ bestimmen.

1. Schritt: Bestimmen der Mittelpunkte

Den Mittelpunkt zwischen zwei Punkten kannst du mithilfe der Ortsvektoren und Verbindungsvektoren berechnen.

$\overrightarrow{OM_1} =\begin{pmatrix}0\\-3\\2,5\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{OM_2}=\begin{pmatrix}0\\3\\2,5\end{pmatrix}$

Vollständige Lösung anzeigen

Um auf die Ortsvektoren der Mittelpunkte zu kommen, benötigst du also zunächst den Ortvektor zu einem der Punkte und dann die Hälfte des Verbindungsvektors zwischen dem Anfangs- und dem Endpunkt. Damit findest du $M_1(0\mid -3 \mid2,5)$ und $M_2(0\mid 3 \mid2,5)$ .

2. Schritt: Darstellung im Koordinatensystem

Zuerst musst du das Koordinatensystem zeichnen. Achte darauf, dass die Achsen weit genug in den positiven und den negativen Bereich gehen, sodass du alle Punkte einzeichnen kannst.

Nachdem du das Koordinatensystem angelegt hast, zeichnest du die Punkte $A$ , $B$ , $C$ und $S$ ein. Verbinde diese daraufhin zu einer Pyramide.

Anschließend zeichnest du die Mittelpunkte $M_1$ und $M_2$ . Diese verbindest du erst miteinander und dann jeweils mit dem Punkt $B$ . So erhältst du die gesuchte Schnittfläche.

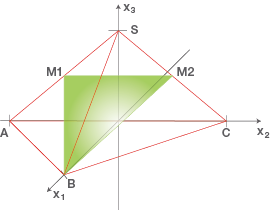Grafik eines geometrischen Figures mit einem grünen Bereich und roten Linien im Koordinatensystem.

Abb. 1: Pyramide und Schnittfläche im Koordinatensystem

$\blacktriangleright$ Berechnung des Umfangs der Schnittfläche

Die Schnittfläche wird von den Kanten $M_1B$ , $M_1M_2$ und $M_2B$ begrenzt. Den Umfang berechnest du, indem du die Länge dieser Kanten, also die Abstände zwischen den Eckpunkten der Fläche berechnest und diese Abstände addierst. Um die Abstände zwischen den Eckpunkten zu berechnen benötigst du im ersten Schritt die Verbindungsvektoren. Im zweiten Schritt musst du die Länge dieser Vektoren berechnen.

1. Schritt: Berechnung der Verbindungsvektoren

$\overrightarrow{M_1B}= \begin{pmatrix}6\\3\\-2,5\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{M_1M_2}= \begin{pmatrix}0\\6\\0\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{M_2B}= \begin{pmatrix}6\\-3\\-2,5\end{pmatrix}$

Vollständige Lösung anzeigen

2. Schritt: Berechnung der Länge der Verbindungsvektoren

Die Länge eines Vektors ist sein Betrag.

$\vert \overrightarrow{M_1B} \vert = \sqrt{51,25}$

$\vert \overrightarrow{M_2B} \vert = \sqrt{51,25}$

$\vert \overrightarrow{M_1M_2} \vert = \sqrt{36}=6$

Vollständige Lösung anzeigen

3. Schritt: Umfang der Schnittfläche berechnen

Der Umfang $(U)$ kannst du jetzt mit den drei Beträgen berechnen:

$U=\sqrt{51,25}+\sqrt{51,25}+6 =20,318$

$\blacktriangleright$ Bestimmen der Koordinatengleichung von $\boldsymbol{E}$

Du sollst nun eine Koordinatengleichung der Ebene $E$ aufstellen, die durch die Punkte $M_1$ , $M_2$ und $B$ verläuft.
Eine Ebenengleichung in Koordinatenform sieht im allgemeinen folgendermaßen aus:

$E:$ $n_1\cdot x_1 +n_2\cdot x_2 +n_3\cdot x_3$ $= a$

Dabei ist $\overrightarrow{n} = \begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}$ ein Normalenvektor zur Ebene $E$ , also ein Vektor, der senkrecht auf der Ebene steht. Ein solcher Normalenvektor ergibt sich aus dem Kreuzprodukt zweier Vektoren, die in der Ebene liegen. Der Parameter $a$ kann über eine Punktprobe bestimmt werden.
Gehe also wie folgt vor:

Berechne einen Normalenvektor von $E$ mit Hilfe des Kreuzproduktes zweier Verbindungsvektoren der Punkte $M_1$ , $M_2$ und $B$

Führe eine Punktprobe durch um $a$ zu bestimmen

Stelle die Ebenengleichung auf

1. Schritt: Bestimmen des Normalenvektors

Zwei Vektoren, die in $E$ liegen erhältst du zum Beispiel mit den Verbindungsvektoren $\overrightarrow{M_1B}$ und $\overrightarrow{M_1M_2}$ . Diese Vektoren hast du bereits im vorherigen Aufgabenteil berechnet:

$\overrightarrow{M_1B}=\begin{pmatrix}6\\3\\-2,5\end{pmatrix}$

$\overrightarrow{M_1M_2}=\begin{pmatrix}0\\6\\0\end{pmatrix}$

Berechne nun $\overrightarrow{n}$ mit Hilfe des Kreuzproduktes:

$\begin{array}[t]{rll} \overrightarrow{n}&=&\overrightarrow{M_1B}\times \overrightarrow{M_1M_2} \\[5pt] &=&\begin{pmatrix}6\\3\\-2,5\end{pmatrix}\times\begin{pmatrix}0\\6\\0\end{pmatrix} \\[5pt] &=&\begin{pmatrix}15\\0\\36\end{pmatrix} \\[5pt] \end{array}$

2. Schritt: Punktprobe

Nun lautet die bisherige Ebenengleichung $E: 15\cdot x_1 + 0\cdot x_2 +36\cdot x_3 = a$
Setze hier nun die Koordinaten eines Punktes der Ebene ein und berechne so $a$ . Wähle dazu beispielsweise $B(6\mid 0 \mid 0)$ :

$a = 15 \cdot 6 + 0\cdot 0 + 36\cdot 0 = 90$

3. Schritt: Ebenengleichung aufstellen

Die Ebenengleichung in Koordinatenform lautet nun :

$E: 15\cdot x_1 +36\cdot x_3 =90$
Da du bei Gleichungen Äquivalenzumformungen durchführen darfst, kannst du auf beiden Seiten der Gleichung durch $3$ teilen und erhältst

$E: 5\cdot x_1 +12\cdot x_3 =30$ , Was als Teilergebins angegeben ist.

$\blacktriangleright$ Bestimmung der Koordinaten von Q

Die Punkte $M_1$ , $M_2$ und $Q$ sollen ein rechtwinkliges Dreieck bilden. Das bedeutet, dass zwischen genau zwei der Verbindungsvektoren $\overrightarrow{M_1M_2}$ , $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$ ein rechter Winkel liegt. Du weißt, dass das Skalarprodukt der Verbindungsvektoren null ist, wenn zwischen diesen ein rechter Winkel liegt.

Achtung: An dieser Stelle kannst du noch nicht sagen zwischen welchen der Verbindungsvektoren der rechte Winkel liegt! Das wird erst in Schritt 2 deutlich.

Gehe wie folgt vor:

Bestimme die allgemeine Form des Punktes $Q_t$ , der auf der Kante $BS$ liegt.

Berechne die Verbindungsvektoren $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$ .

Berechne das Skalarprodukt und setzte es mit Null gleich um $Q$ zu bestimmen.

1. Schritt: Bestimmen des Punktes $Q_t$ allgemein

Du weißt, dass $Q$ auf der Kante $BS$ liegt. Also auf einer Geraden durch die Punkte $B$ und $S$ . Die Gerade durch $B$ und $S$ kannst du aufstellen, indem du als Stützvektor den Ortsvekter $\overrightarrow{OB}$ und als Spannvektor den Verbindungsvektor $\overrightarrow{BS}$ wählst. Also folgt:

$\overrightarrow{OB}=\begin{pmatrix}6\\0\\0\end{pmatrix}\$ und

$\ \overrightarrow{BS}=\begin{pmatrix}-6\\0\\5\end{pmatrix}$

Vollständige Lösung anzeigen

Damit findest du die Geradengleichung

$g: \ \ \overrightarrow{x}= \begin{pmatrix}6\\0\\0\end{pmatrix}+ t \cdot \begin{pmatrix}-6\\0\\5\end{pmatrix}$ Jeder Punkt auf dieser Gerade hat die Form $Q_t (6 -6 t\mid 0 \mid 5t )$

2. Schritt: Berechnung der Verbindungsvektoren $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$

Die Verbindungsvektoren berechnest du über die Differenz der Ortsvektoren:

$\overrightarrow{M_1Q} = \begin{pmatrix}6-6t\\3\\-2,5+5t\end{pmatrix}$

$\overrightarrow{M_2Q} =\begin{pmatrix}6-6t\\-3\\-2,5+5t\end{pmatrix}$

Vollständige Lösung anzeigen

Den Verbindungsvektor $\overrightarrow{M_1M_2}=\begin{pmatrix}0\\6\\0\end{pmatrix}$ hast du bereits im vorherigen Aufgabenteil berechnet.

Im nächsten Schritt sollst du das Skalsrprodukt berechnen und dieses mit Null gleichsetzen. Du kannst bereits an dieser Stelle erkennen, dass die Skalarprodukte

$\overrightarrow{M_1Q} \circ \overrightarrow{M_1M_2} = 18$

Vollständige Lösung anzeigen

und $\overrightarrow{M_1Q} \cdot \overrightarrow{M_1M_2} = -18$

für kein t null werden können. Der rechte Winkel muss also zwischen $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$ liegen.

Schritt 3: Berechnung des Skalarprodukts und Bestimmung von $Q$

Das Skalarprodukt zwischen den Verbindungsvektoren lautet

$\overrightarrow{M_1Q} \circ \overrightarrow{M_2Q} = ...$

Vollständige Lösung anzeigen

Jetzt sollst du $t$ so wählen, dass das Skalarprodukt null ist. Dazu kannst du den Taschenrechner verwenden. Gebe den oberen Term $(6-6t)^2 -9+(5t-2,5)^2$ als Funktion in den GTR ein und berechne die Nullstellen mit folgendem Befehl:

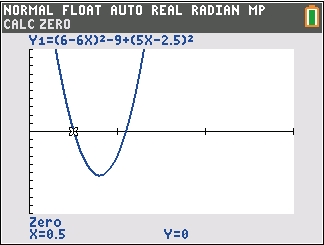
2ND $\to$ TRACE (CALC) $\to$ 2: zero

$\begin{array}[t]{rll} t_1 &=& 0,5 \\ t_2&=& 1,09 \end{array}$

Vollständige Lösung anzeigen

Grafik einer Parabel, dargestellt auf einem Taschenrechner-Display mit Achsen und Gleichung.

Abb. 2 Bestimmen der Nullstellen

Du hast jetzt zwei Lösungen für $t$ gefunden. Setzt du $t_2$ in den allgemeinen Punkt $Q_t$ ein, so erhältst du einen Punkt, der nicht zwischen $B$ und $S$ liegt und somit nicht auf der Kante $BS$ . Setzt du $t_1$ ein, erhältst du den gesuchten Punkt $Q(6-6\cdot 0,5\mid 0 \mid 5 \cdot 0,5)$ also $Q(3\mid 0 \mid 2,5)$ .

$\blacktriangleright$ Bestimmung der Koordinaten von $\boldsymbol{Z}$

Du kannst aus der Aufgabenstellung entnehmen, dass $Z$ in der $x_1x_2$ -Ebene und im Inneren der Pyramide $ABCS$ liegt. Außerdem soll $Z$ zu der Grundfläche $ABC$ , der Seitenfläche $ACS$ und zu der Ebene $E$ den gleichen Abstand haben. Da der Punkt in der $x_1x_3-$ Ebene liegt, ist die zweite Komponente null, hat also die allgemeine Form:

$Z= \begin{pmatrix}x_1\\0\\x_3\end{pmatrix}$

Gehe wie Folgt vor:

Bestimme die Ebenengleichungen der drei Ebenen in Koordinatenform.

Berechne mithilfe der Hesseschen Normalform die Abstände zwischen den drei Ebenen und Punkt $Z$ in allgemeiner Form.

Bestimme die Koordinaten des Punktes $Z$ , indem du die Abstände aus Schritt 2 gleichsetzt.

Schritt 1: Bestimmen der Ebenengleichungen

Die Ebenengleichung von $E$ hast du bereits in Aufgabenteil a) bestimmt.

$E: 5\cdot x_1 +12\cdot x_3 =30$

Betrachtest du die Koordinaten der Punkte $A$ , $B$ und $C$ kannst du sehen, dass $A$ und $C$ auf der $x_2$ Achse und $B$ auf der $x_1$ -Achse liegen. Die Ebene $ABC$ liegt also in der $x_1x_2$ -Ebene und besitzt damit die gleiche Koordinatengleichung, wie die $x_1x_2$ -Ebene.

$ABC: x_3=0$

Es fehlt also nur noch die Koordinatengleichung der Ebene $ACS$ . Die Punkte $A$ und $C$ liegen, wie bereits erwähnt auf der $x_2-$ Achse. $S$ liegt auf der $x_3-$ Achse. Die Ebene $ACS$ liegt also in der $x_2x_3-$ Ebene und hat damit die gleiche Koordinatengleichung, wie die $x_2x_3-$ Ebene.

$ACS: x_1=0$

Dass die Ebenen $ABC$ und $ACS$ in den Koordinatenebenen liegen kannst du auch aus deiner Zeichung im Aufgabenteil a) entnehmen.

Schritt 2: Abstandsberechnung mit der Hesseschen Normalform

Mit der Hesseschen Normalform kannst du den Abstand $d$ zwischen einem Punkt $P(x_1 \mid x_2 \mid x_2)$ und einer Ebene in Koordinatenform (siehe Aufgabenteil a)) berechnen.

$d=$ $\frac{|n_1x_1+n_2x_2+n_3x_3-a|}{\vert{n}\vert}$

Im Nenner steht der Betrag des Normalenvektors. Du musst nun für alle drei Ebenen den Abstand zwischen dem Punkt $Z(x_1 \mid 0 \mid x_3)$ bestimmen. Dazu brauchst du die Beträge der Normalenvektoren. Die Normalenvektoren kannst du aus der Koordinatenform der Ebenen ablesen.

$n_E=\begin{pmatrix}5\\0\\12\end{pmatrix}$ $\rightarrow$ $|n_E|=\sqrt{5^2+12^2}=13$

$n_{ABC}=\begin{pmatrix}0\\0\\1\end{pmatrix}$ $\rightarrow$ $|n_{ABC}|=\sqrt{1}=1$

$n_{ACS}= \begin{pmatrix}1\\0\\0\end{pmatrix}$ $\rightarrow$ $|n_{ACS}|=\sqrt{1}=1$

Jetzt kannst du alle bekannten Werte in die Hessesche Normalform einsetzten. Im Folgenden ist $d_E$ der Abstand von $Z$ zur Ebene $E$ usw.

$d_E=\frac{|5x_1+12x_3-30|}{13}$

$d_{ABC}=\frac{|0 \cdot x_1+1x_3-0|}{1} = x_3$

$d_{ACS}=\frac{|1 \cdot x_1+0 \cdot x_3-0|}{1}=x_1$

Die Koordinaten $x_1$ und $x_3$ müssen jetzt so gewählt werden, dass alle drei Abstände gleich groß sind. Also:

$d=\frac{5x_1+12x_3-30}{13}=x_1=x_3$ ,

woraus direkt $x_1=x_3$ folgt. Du kannst also in dem Bruch $x_3$ durch $x_1$ ersetzten und erhältst:

$\begin{array}[t]{rll} d&=&\frac{\vert \ 5x_1+12x_1-30 \ \vert}{13} &=& x_1\\[5pt] d &=&\frac{\vert \ 17x_1-30 \ \vert}{13} & =& x_1 \quad \scriptsize \mid\; \cdot 13\\ & & \vert \ 17x_1-30 \ \vert & =& 13 x_1\\ \end{array}$

Durch den Betrag erhält man für $x_1$ zwei Lösungen zum Einen:

$\begin{array}[t]{rll} 17 x_1 -30&=& 13 x_1 \quad \scriptsize \mid \; -17 x_1 \\[5pt] -4 x_1&=& -30 \quad \scriptsize \mid \;: (-4) \\[5pt] x_1 &=& 7,5 \end{array}$

und zum Anderen:

$\begin{array}[t]{rll} -(17 x_1 -30)&=& 13 x_1 \quad \scriptsize \mid \; +17 x_1 \\[5pt] 30 x_1&=& 30 \quad \scriptsize \mid \; :30 \\[5pt] x_1&=& 1 \end{array}$

Da $Z$ für $x_1=7,5$ nicht in der Pyramide liegt, ist $x_1=1$ die richtige Lösung und die Koordinaten sind $Z(1 \mid 0 \mid 1)$

Aufgabe 2.2.

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass alle Fortgeschrittenenpaare anwesend sind.

Um die Wahrscheinlichkeit zu berechnen kannst du die Zufallsvariable $X_F$ betrachten, welche die Anzahl der Fortgeschrittenenpaare beschreibt, die anwesend sind. Diese Zufallsvariable kann als binomialverteilt mit den Parametern $n=4$ und $p=0,75$ angenommen werden.Da in der Aufgabenstellung angegeben ist, dass die Anzahl der Fortgeschrittenenpaare gleich vier ist und dass sie mit einer Wahrscheinlichkeit von 75 $%$ an der Tanzgruppe teilnehmen.

$P(X_F=4)=0,75^4 \approx 0,316$

Mit einer Wahrscheinlichkeit von $32 \%$ sind also alle Fortgeschrittenenpaare anwesend.

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass mindestens 6 Anfängerpaare und höchstens 3 Fortgeschrittenenpaare anwesend sind.

Du musst in diesem Aufgabenteil noch eine weitere Zufallsvariable $X_A$ , für die Anzahl der anwesenden Anfängerpaare betrachten. Diese Zufallsvariable kann ebenfalls als binomialverteilt angenommen werden und hat die Parameter $n=8$ und $p=0,9$ . Betrachte zuerst die beiden Wahrscheinlichkeiten

$P(X_F \le 3)$ und $P(X_A \ge 6)$ . Diese Wahrscheinlichkeiten kannst du wie folgt berechnen:

$\begin{array}[t]{rll} P(X_F \le 3)&=&1 - P(X_F =4) \\[5pt] &=& 1- 0,75^4 \\[5pt] &\approx& 0,684 \\[5pt] \end{array}$

$P(X_A \ge 6) \approx 0,962$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit dafür, sowohl mindestens 6 Anfängerpaare als auch höchstens 3 Fortgeschrittenenpaare anwesend sind kannst du durch das Produkt der Wahrscheinlichkeiten $P(X_F \le 3)$ und $P(X_A \ge 6)$ bestimmen.

$P(X_F \le 3) \cdot P(X_A \ge 6) \approx 0,658$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit beträgt also ca. $66\%$ .

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass mindestens 11 Paare anwesend sind.

Es gibt zwei Möglichkeiten dafür, dass 11 Paare anwesend sind. Entweder es sind 7 Anfängerpaare und 4 Fortgeschrittenenpaare oder alle 8 Anfängerpaare und 3 Fortgeschrittenenpaare anwesend. Außerdem gibt es genau eine Möglichkeit, dass alle 12 Paare anwesend sind. Betrachte die Zufallsvariable $Y$ , welche die Anzahl der anwesenden Paare beschreibt. Dann lässt sich die gesuchte Wahrscheinlichkeit wie Folgt darstellen.

$P(Y \ge 11)\approx 0,439$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit dafür, dass mindestens 11 Paare anwesend sind, beträgt somit $44 \%$ .

Du kannst die Wahrscheinlichkeiten auch mit dem GTR berechnen. Dafür verwendest du den binompdf Befehl, welchen du wie folgt findest:

2ND VARS(DISTR) A: binompdf

Die Wahrscheinlichkeit $P(X_F=4)$ kannst du beispielsweise bestimmen, indem du die Parameter $n=4$ , $p=0,75$ und $k=4$ der Reihe nach eingibst.

Screenshot eines Taschenrechners mit binomischer Wahrscheinlichkeit und Eingabewerten.

Abb. 3 Eingetragene Daten

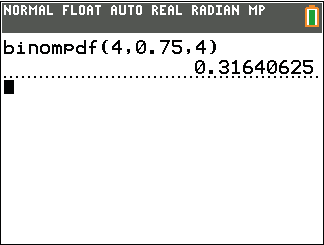Bildschirmansicht eines Taschenrechners mit einer Berechnung zur Binomialverteilung.

Abb. 4 Lösung mit dem GTR

Die mit dem GTR berechnete Lösung entspricht deiner Lösung aus Aufgabenteil a).

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

Aufgabe 2.1

$\blacktriangleright$ Darstellung der Pyramide und der Schnittfläche im Koordinatensystem

Schritt 1: Bestimmen der Mittelpunkte

Den Mittelpunkt zwischen zwei Punkten kannst du mithilfe der Ortsvektoren und Verbindungsvektoren berechnen.

$\overrightarrow{OM_1}=\begin{pmatrix}0\\-3\\2,5\end{pmatrix}$

Vollständige Lösung anzeigen

$\overrightarrow{OM_2} =\begin{pmatrix}0\\3\\2,5\end{pmatrix}$

Vollständige Lösung anzeigen

Schritt 2: Darstellung im Koordinatensystem

Zuerst musst du das Koordinatensystem zeichnen. Achte darauf, dass die Achsen weit genug in den positiven und den negativen Bereich gehen, sodass du alle Punkte einzeichnen kannst.

Nachdem du das Koordinatensystem angelegt hast, zeichnest du die Punkte $A$ , $B$ , $C$ und $S$ ein. Verbinde diese daraufhin zu einer Pyramide.

Anschließend zeichnest du die Mittelpunkte $M_1$ und $M_2$ . Diese verbindest du erst miteinander und dann jeweils mit dem Punkt $B$ . So erhältst du die gesuchte Schnittfläche.

Abb. 1: Pyramide und Schnittfläche im Koordinatensystem

$\blacktriangleright$ Berechnung des Umfangs der Schnittfläche

Schritt 1: Berechnung der Verbindungsvektoren

$\overrightarrow{M_1B}=\begin{pmatrix}6\\3\\-2,5\end{pmatrix}$

$\overrightarrow{M_1M_2}=\begin{pmatrix}0\\6\\0\end{pmatrix}$

$\overrightarrow{M_2B}=\begin{pmatrix}6\\-3\\-2,5\end{pmatrix}$

Vollständige Lösung anzeigen

Schritt 2: Berechnung der Länge der Verbindungsvektoren

Die Länge eines Vektors ist sein Betrag.

$\vert \overrightarrow{M_1B} \vert = \sqrt{51,25}$

$\vert \overrightarrow{M_2B} \vert = \sqrt{51,25}$

$\vert \overrightarrow{M_1M_2} \vert = \sqrt{36}=6$

Vollständige Lösung anzeigen

Schritt 3: Umfang der Schnittfläche berechnen

Der Umfang $(U)$ kannst du jetzt mit den drei Beträgen berechnen:

$U=20,318$

Vollständige Lösung anzeigen

$\blacktriangleright$ Bestimmen der Koordinatengleichung von $\boldsymbol{E}$

$E:$ $n_1\cdot x_1 +n_2\cdot x_2 +n_3\cdot x_3$ $= a$

Berechne einen Normalenvektor von $E$ mit Hilfe des Kreuzproduktes zweier Verbindungsvektoren der Punkte $M_1$ , $M_2$ und $B$

Führe eine Punktprobe durch um $a$ zu bestimmen

Stelle die Ebenengleichung auf

1. Schritt: Bestimmen des Normalenvektors

$\overrightarrow{M_1B}=\begin{pmatrix}6\\3\\-2,5\end{pmatrix}$

$\overrightarrow{M_1M_2}=\begin{pmatrix}0\\6\\0\end{pmatrix}$

Berechne nun $\overrightarrow{n}$ mit Hilfe des Kreuzproduktes:

2. Schritt: Punktprobe

$a = 15 \cdot 6 + 0\cdot 0 + 36\cdot 0 = 90$

3. Schritt: Ebenengleichung aufstellen

Die Ebenengleichung in Koordinatenform lautet nun :

$E: 15\cdot x_1 +36\cdot x_3 =90$
Da du bei Gleichungen Äquivalenzumformungen durchführen darfst, kannst du auf beiden Seiten der Gleichung durch $3$ teilen und erhältst

$E: 5\cdot x_1 +12\cdot x_3 =30$ , Was als Teilergebins angegeben ist.

$\blacktriangleright$ Bestimmung der Koordinaten von Q

Achtung: An dieser Stelle kannst du noch nicht sagen zwischen welchen der Verbindungsvektoren der rechte Winkel liegt! Das wird erst in Schritt 2 deutlich.

Gehe wie folgt vor:

Bestimme die allgemeine Form des Punktes $Q_t$ , der auf der Kante $BS$ liegt.

Berechne die Verbindungsvektoren $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$ .

Berechne das Skalarprodukt und setzte es mit Null gleich um $Q$ zu bestimmen.

1. Schritt: Bestimmen des Punktes $Q_t$ allgemein

$\overrightarrow{OB}=\begin{pmatrix}6\\0\\0\end{pmatrix}\$ und

$\overrightarrow{BS}=\begin{pmatrix}-6\\0\\5\end{pmatrix}$

Vollständige Lösung anzeigen

Damit findest du die Geradengleichung

$g: \ \ \overrightarrow{x}= \begin{pmatrix}6\\0\\0\end{pmatrix}+ t \cdot \begin{pmatrix}-6\\0\\5\end{pmatrix}$ Jeder Punkt auf dieser Gerade hat die Form $Q_t (6 -6 t\mid 0 \mid 5t )$

2. Schritt: Berechnung der Verbindungsvektoren $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$

Die Verbindungsvektoren berechnest du über die Differenz der Ortsvektoren:

$\overrightarrow{M_1Q} = \begin{pmatrix}6-6t\\3\\-2,5+5t\end{pmatrix}$

$\overrightarrow{M_2Q} =\begin{pmatrix}6-6t\\-3\\-2,5+5t\end{pmatrix}$

Vollständige Lösung anzeigen

Den Verbindungsvektor $\overrightarrow{M_1M_2}=\begin{pmatrix}0\\6\\0\end{pmatrix}$ hast du bereits im vorherigen Aufgabenteil berechnet.

Im nächsten Schritt sollst du das Skalsrprodukt berechnen und dieses mit Null gleichsetzten. Du kannst bereits an dieser Stelle erkennen, dass die Skalarprodukte

$\overrightarrow{M_1Q} \circ \overrightarrow{M_1M_2} = -18$

Vollständige Lösung anzeigen

für kein t null werden können. Der rechte Winkel muss also zwischen $\overrightarrow{M_1Q}$ und $\overrightarrow{M_2Q}$ liegen.

3. Schritt: Berechnung des Skalarprodukts und Bestimmung von $Q$

Das Skalarprodukt zwischen den Verbindungsvektoren lautet

$\overrightarrow{M_1Q} \circ \overrightarrow{M_2Q} = ...$

Vollständige Lösung anzeigen

F5 (G-Solv) $\to$ F1 (ROOT)

$\begin{array}[t]{rll} t_1 &=& 0,5 \\ t_2&=& 1,09 \end{array}$

Vollständige Lösung anzeigen

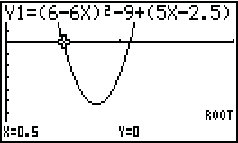Graf einer quadratischen Funktion mit einer Wurzel, Achsen und Koordinaten.

Abb. 2 Berechnung der Nullstellen

$\blacktriangleright$ Bestimmung der Koordinaten von $\boldsymbol{Z}$

$Z= \begin{pmatrix}x_1\\0\\x_3\end{pmatrix}$

Gehe wie Folgt vor:

Bestimme die Ebenengleichungen der drei Ebenen in Koordinatenform.

Berechne mithilfe der Hesseschen Normalform die Abstände zwischen den drei Ebenen und Punkt $Z$ in allgemeiner Form.

Bestimme die Koordinaten des Punktes $Z$ , indem du die Abstände aus Schritt 2 gleichsetzt.

Schritt 1: Bestimmen der Ebenengleichungen

Die Ebenengleichung von $E$ hast du bereits in Aufgabenteil a) bestimmt.

$E: 5\cdot x_1 +12\cdot x_3 =30$

$ABC: x_3=0$

$ACS: x_1=0$

Dass die Ebenen $ABC$ und $ACS$ in den Koordinatenebenen liegen kannst du auch aus deiner Zeichung im Aufgabenteil a) entnehmen.

Schritt 2: Abstandsberechnung mit der Hesseschen Normalform

Mit der Hesseschen Normalform kannst du den Abstand $d$ zwischen einem Punkt $P(x_1 \mid x_2 \mid x_2)$ und einer Ebene in Koordinatenform (siehe Aufgabenteil a)) berechnen.

$d=$ $\frac{|n_1x_1+n_2x_2+n_3x_3-a|}{\vert{n}\vert}$

$n_E=\begin{pmatrix}5\\0\\12\end{pmatrix}$ $\rightarrow$ $|n_E|=\sqrt{5^2+12^2}=13$

$n_{ABC}=\begin{pmatrix}0\\0\\1\end{pmatrix}$ $\rightarrow$ $|n_{ABC}|=\sqrt{1}=1$

$n_{ACS}= \begin{pmatrix}1\\0\\0\end{pmatrix}$ $\rightarrow$ $|n_{ACS}|=\sqrt{1}=1$

Jetzt kannst du alle bekannten Werte in die Hessesche Normalform einsetzten. Im Folgenden ist $d_E$ der Abstand von $Z$ zur Ebene $E$ usw.

$d_E=\frac{|5x_1+12x_3-30|}{13}$

$d_{ABC}=\frac{|0 \cdot x_1+1x_3-0|}{1} = x_3$

$d_{ACS}=\frac{|1 \cdot x_1+0 \cdot x_3-0|}{1}=x_1$

Die Koordinaten $x_1$ und $x_3$ müssen jetzt so gewählt werden, dass alle drei Abstände gleich groß sind. Also:

$d=\frac{5x_1+12x_3-30}{13}=x_1=x_3$ ,

woraus direkt $x_1=x_3$ folgt. Du kannst also in dem Bruch $x_3$ durch $x_1$ ersetzten und erhältst:

$\begin{array}[t]{rll} d&=&\frac{\vert \ 5x_1+12x_1-30 \ \vert}{13} &=& x_1\\[5pt] d &=&\frac{\vert \ 17x_1-30 \ \vert}{13} & =& x_1 \quad \scriptsize \mid\ \cdot 13\\ & & \vert \ 17x_1-30 \ \vert & =& 13 x_1\\ \end{array}$

Durch den Betrag erhält man für $x_1$ zwei Lösungen zum Einen:

$\begin{array}[t]{rll} 17 x_1 -30&=& 13 x_1 \quad \scriptsize \mid \; -17 x_1 \\[5pt] -4 x_1&=& -30 \quad \scriptsize \mid \; \div (-4) \\[5pt] x_1 &=& 7,5 \end{array}$

und zum Anderen:

$\begin{array}[t]{rll} -(17 x_1 -30)&=& 13 x_1 \quad \scriptsize \mid \; +17 x_1 \\[5pt] 30 x_1&=& 30 \quad \scriptsize \mid \; \div 30 \\[5pt] x_1&=& 1 \end{array}$

Da $Z$ für $x_1=7,5$ nicht in der Pyramide liegt, ist $x_1=1$ die richtige Lösung und die Koordinaten sind $Z(1 \mid 0 \mid 1)$

Aufgabe 2.2

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass alle Fortgeschrittenenpaare anwesend sind.

$P(X_F=4)=0,75^4 \approx 0,316$

Mit einer Wahrscheinlichkeit von $32 \%$ sind also alle Fortgeschrittenenpaare anwesend.

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass mindestens 6 Anfängerpaare und höchstens 3 Fortgeschrittenenpaare anwesend sind.

$P(X_F \le 3)$ und $P(X_A \ge 6)$ . Diese Wahrscheinlichkeiten kannst du wie folgt berechnen:

$\begin{array}[t]{rll} P(X_F \le 3)&=& 1 - P(X_F =4) \\[5pt] &=& 1- 0,75^4 \\[5pt] &\approx& 0,684 \\[5pt] \end{array}$

$P(X_A \ge 6) \approx 0,962$

Vollständige Lösung anzeigen

$P(X_F \le 3) \cdot P(X_A \ge 6) \approx 0,658$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit beträgt also $66\%$ .

$\blacktriangleright$ Wahrscheinlichkeit dafür, dass mindestens 11 Paare anwesend sind.

$P(Y \ge 11) \approx 0,439$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit dafür, dass mindestens 11 Paare anwesend sind, beträgt somit $44 \%$ .

Du kannst Wahrscheinlichkeiten auch mit deinem Taschenrechner berechnen.

Dafür verwendest du den binompdf-Befehl deines GTR. Diesen findest du im Statistik-Menü unter

F5: DIST F5: Binomial F1: Bpd F2: Var

Die Wahrscheinlichkeit 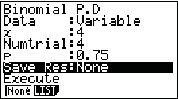$\mathbb{P}(X_F=4)$ kannst du beispielsweise bestimmen, indem du die Parameter $n=4$ , $p=0,75$ und $k=4$ der Reihe nach eingibst.

Bildschirmansicht eines Taschenrechners mit binomialen Berechnungen und Variablen.

Abb. 3 Eingegebene Daten

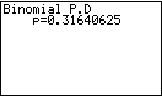Binomialverteilung mit P-Wert von 0,31640625.

Abb. 4 Lösung mit dem GTR

Die mit dem GTR berechnete Lösung entspricht deiner Lösung aus Aufgabenteil a).

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]