Wahlteil A2
Aufgabe A2.1
Die unten stehende Abbildung zeigt eine Station in einem Bikepark, die aus zwei seitlichen Wällen und einer Fahrrinne besteht.
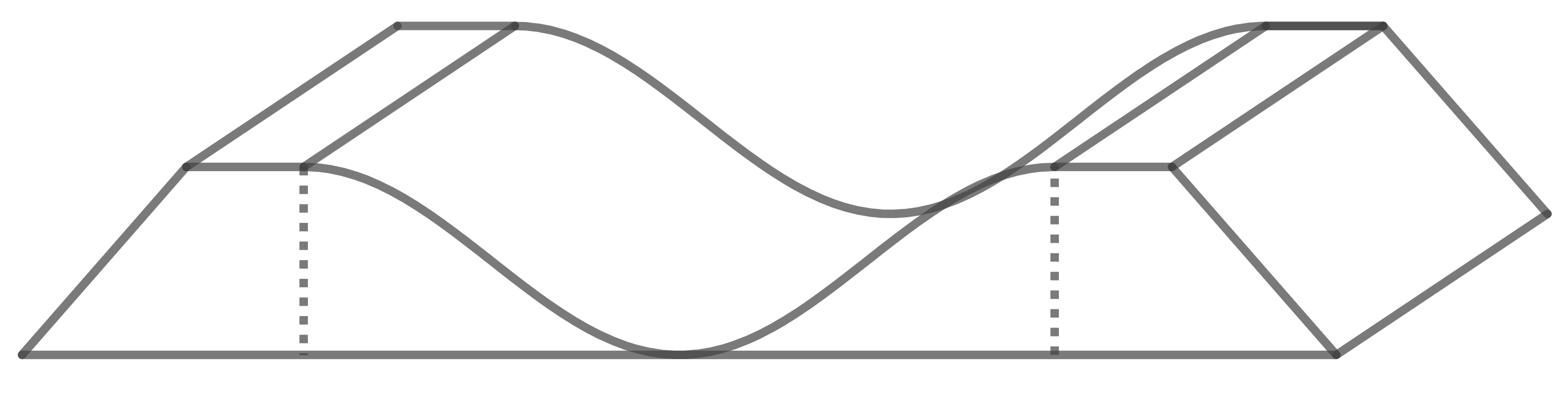 Die Abbildung unten zeigt modelhaft ihren Querschnitt. Dabei wird die Fahrrinne durch den Graphen einer Funktion
Die Abbildung unten zeigt modelhaft ihren Querschnitt. Dabei wird die Fahrrinne durch den Graphen einer Funktion  im Bereich
im Bereich  modelliert (Angaben in Meter).
modelliert (Angaben in Meter).
Die Querschnitte der Wälle sind grau markiert. Der horizontale Untergrund wird im Querschnitt durch die -Achse beschrieben. Die Station hat auf ihrer gesamten Länge den in der Abbildung gezeigten Querschnitt.
-Achse beschrieben. Die Station hat auf ihrer gesamten Länge den in der Abbildung gezeigten Querschnitt.
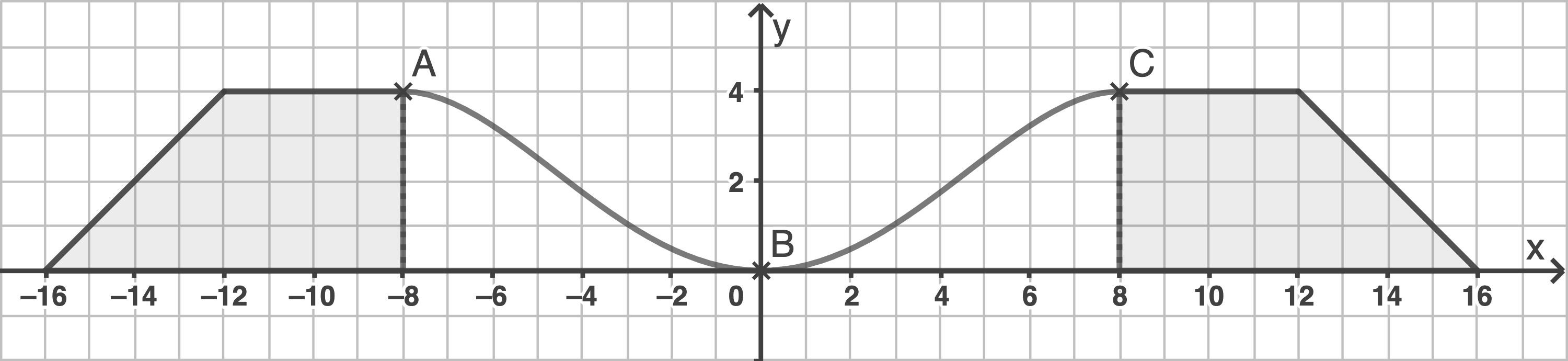

Die Querschnitte der Wälle sind grau markiert. Der horizontale Untergrund wird im Querschnitt durch die

a)
Bearbeite die folgenden Aufgabenstellungen anhand des oben abgebildeten Graphen:
Bestimme die Breite der Fahrrinne in einer Höhe von  über dem Untergrund.
über dem Untergrund.
Ermittle die mittlere Steigung zwischen den im Modell mit und
und  bezeichneten Punkten.
bezeichneten Punkten.
Bestimme die maximale Steigung der Fahrrinne.
Begründe, dass keine ganzrationale Funktion zweiten Grades sein kann.
keine ganzrationale Funktion zweiten Grades sein kann.
Ermittle die mittlere Steigung zwischen den im Modell mit
Bestimme die maximale Steigung der Fahrrinne.
Begründe, dass
(4,5 VP)
b)
Es ist  .
Berechne die Höhe, in der die Fahrrinne eine Breite von
.
Berechne die Höhe, in der die Fahrrinne eine Breite von  hat. Das verbaute Material hat ein Gesamtvolumen von
hat. Das verbaute Material hat ein Gesamtvolumen von  .
Ermittle die Länge der Station.
.
Ermittle die Länge der Station.
(5 VP)
c)
Die abgebildete Fahrrinne lässt sich auch näherungsweise durch den Graphen einer trigonometrischen Funktion  modellieren, der die Punkte
modellieren, der die Punkte  ,
,  und
und  als Extrempunkte besitzt.
Bestimme einen möglichen Funktionsterm von
als Extrempunkte besitzt.
Bestimme einen möglichen Funktionsterm von  .
.
(2,5 VP)
Aufgabe A2.2
Gegeben ist die Funktion  durch
durch  ;
;
Ihr Graph sowie die Gerade
sowie die Gerade  sind in der unten stehenden Abbildung dargestellt.
sind in der unten stehenden Abbildung dargestellt.
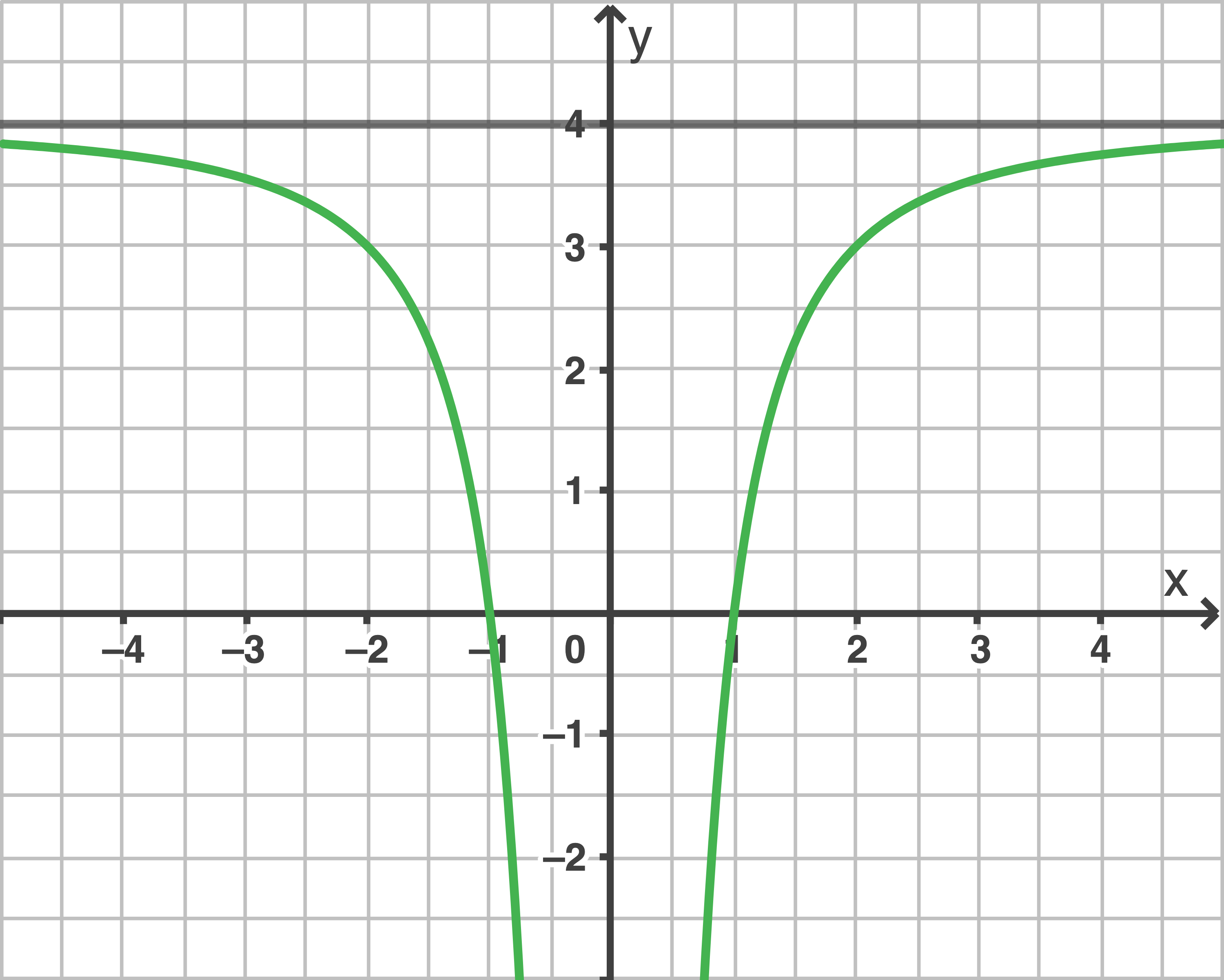
 ist der Graph der Funktion
ist der Graph der Funktion  mit
mit 
 geht durch eine Streckung in
geht durch eine Streckung in  -Richtung und eine Streckung in
-Richtung und eine Streckung in  -Richtung aus
-Richtung aus  hervor.
Ermittle die beiden zugehörigen Streckfaktoren.
hervor.
Ermittle die beiden zugehörigen Streckfaktoren.
Ihr Graph

a)
Der Punkt  mit
mit  ist ein Punkt auf
ist ein Punkt auf  .
.
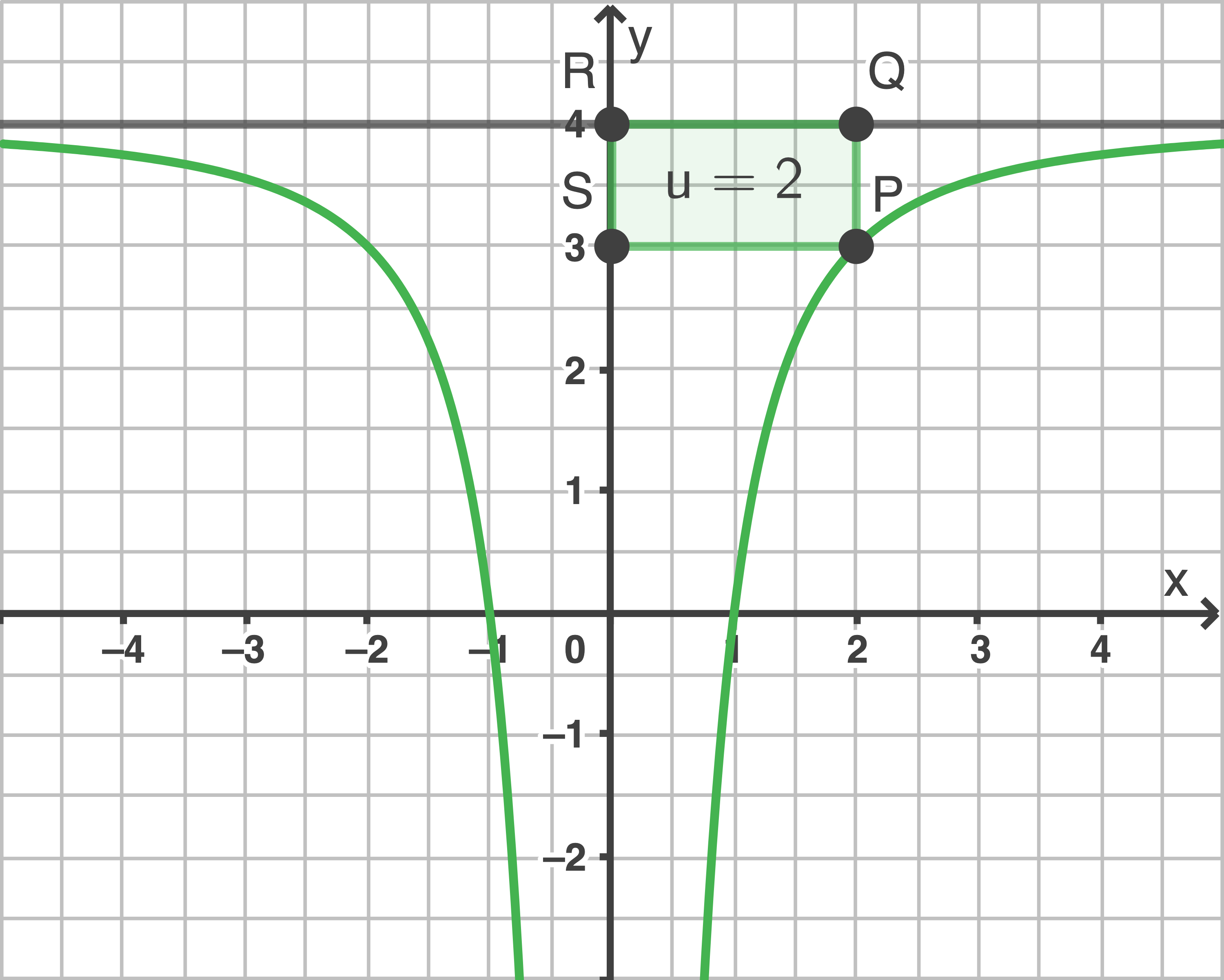
Die Punkte ,
,  ,
,  und
und  sind die Ecken eines Rechtecks.
sind die Ecken eines Rechtecks.
Bei Rotation dieses Rechtecks um die -Achse entsteht ein Zylinder.
Zeige, dass das Volumen dieses Zylinders unabhängig von
-Achse entsteht ein Zylinder.
Zeige, dass das Volumen dieses Zylinders unabhängig von  ist.
Berechne denjenigen Wert von
ist.
Berechne denjenigen Wert von  , für den der Inhalt der Mantelfläche des Zylinders
, für den der Inhalt der Mantelfläche des Zylinders  beträgt.
beträgt.
Die Punkte
Bei Rotation dieses Rechtecks um die
(4 VP)
b)
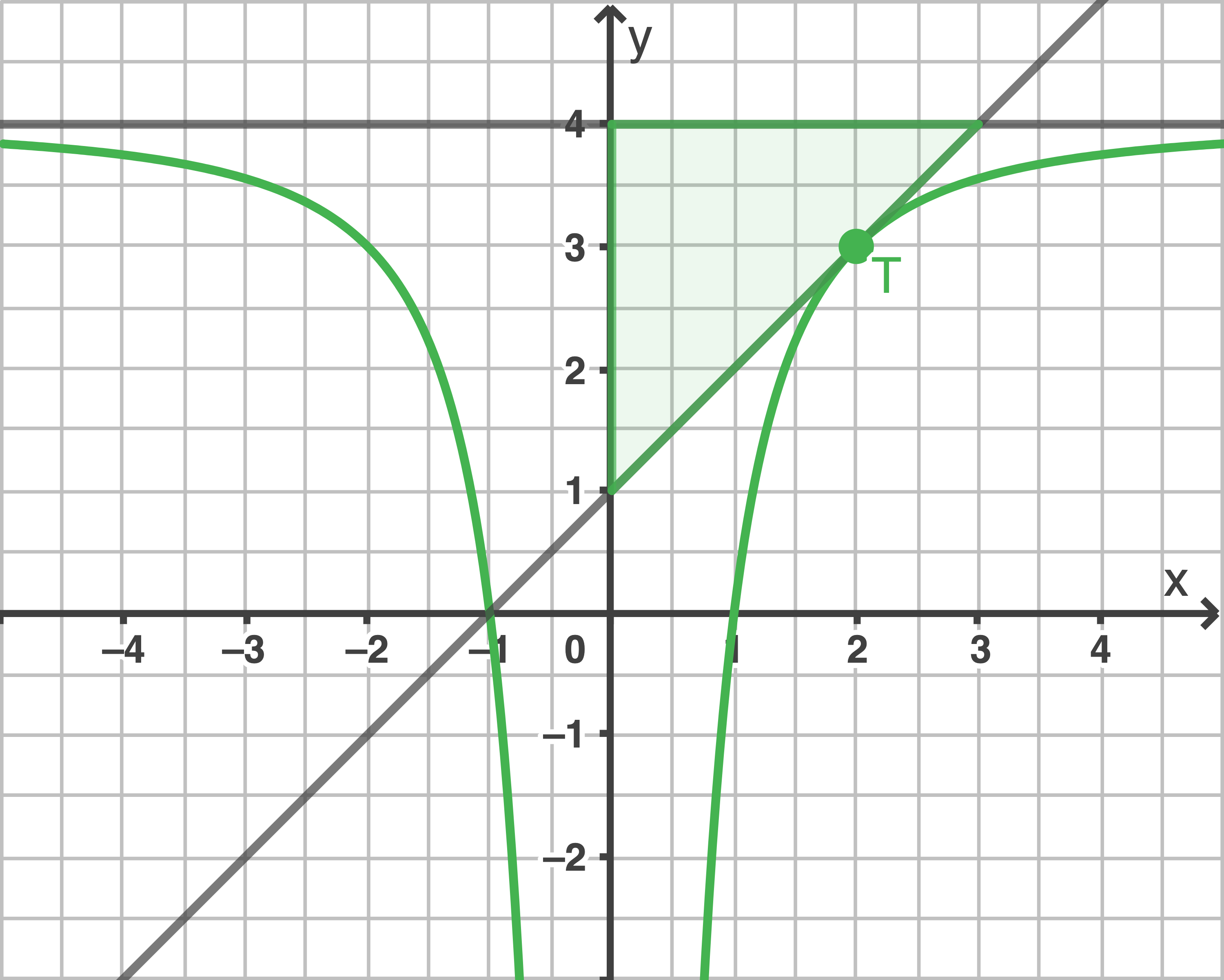
Für jeden Punkt auf  begrenzen die zugehörige Tangente an
begrenzen die zugehörige Tangente an  , die Gerade
, die Gerade  und die
und die  -Achse ein Dreieck. Für einen solchen Punkt
-Achse ein Dreieck. Für einen solchen Punkt  mit positiver
mit positiver  -Koordinate ist dieses Dreieck gleichschenklig.
Berechne die
-Koordinate ist dieses Dreieck gleichschenklig.
Berechne die  -Koordinate dieses Punktes
-Koordinate dieses Punktes  .
.
(2 VP)
c)
(2 VP)
Lösung A 2.1
a)
Breite der Fahrrinne bestimmen
Durch Einzeichnen der Gerade kann man die ungefähren Schnittstellen
kann man die ungefähren Schnittstellen  und
und  ablesen.
ablesen.
Die Breite der Fahrrinne in einer Höhe von einem Meter beträgt also ca. Mittlere Steigung zwischen
Mittlere Steigung zwischen  und
und  ermitteln
ermitteln
Die mittlere Steigung wird mit berechnet.
berechnet.
Somit ist der Wert der mittleren Steigung .
Maximale Steigung der Fahrrinne bestimmen
.
Maximale Steigung der Fahrrinne bestimmen
 Begründen
Begründen
Eine ganzrationalen Funktion zweiten Grades hat keine Wendestelle.
Durch Einzeichnen der Gerade
Die Breite der Fahrrinne in einer Höhe von einem Meter beträgt also ca.
Die mittlere Steigung wird mit
Somit ist der Wert der mittleren Steigung
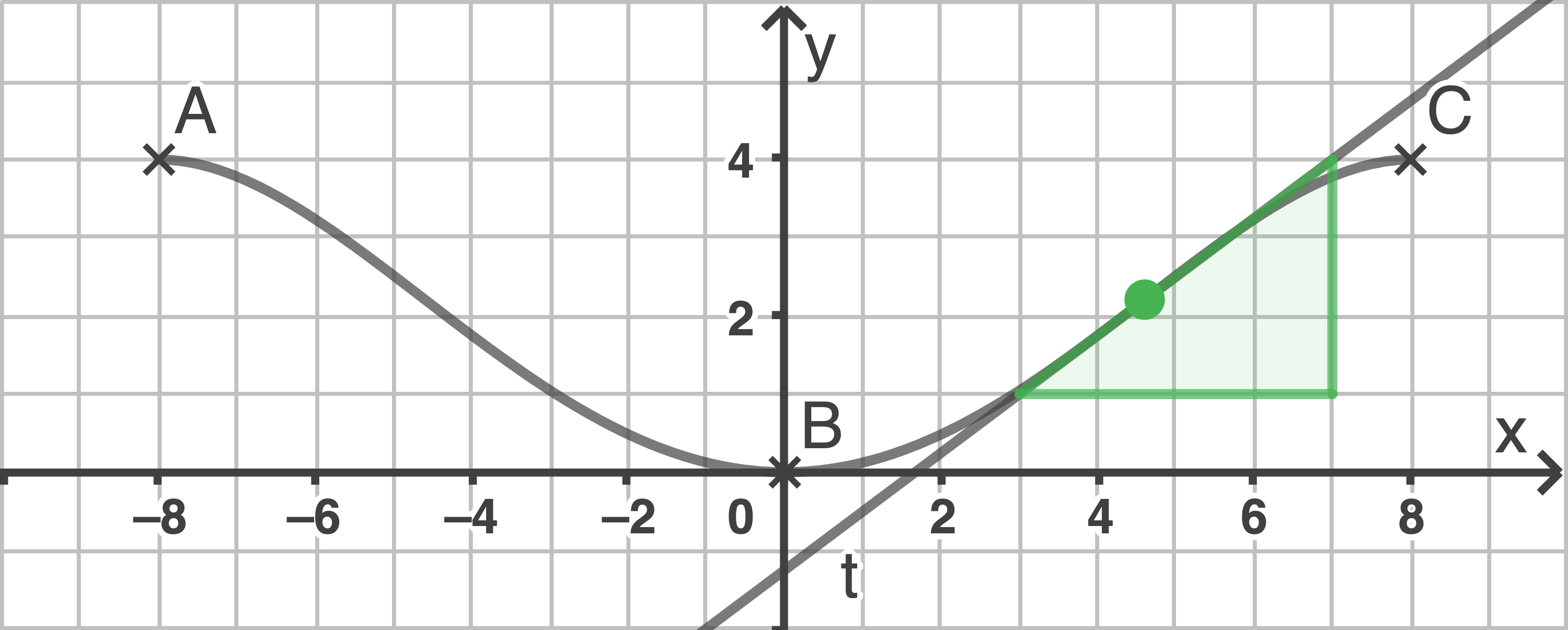
Die maximale Steigung besitzt der Graph der Funktion im Wendepunkt an der Stelle 
Die Steigung der Tangente im Wendepunkt entspricht der maximalen Steigung.
Die Tangente verläuft durch die Punkte und
und  .
.
Mit dem Steigungsdreieck lässt sich die Steigung berechnen:
Die Steigung der Tangente im Wendepunkt entspricht der maximalen Steigung.
Die Tangente verläuft durch die Punkte
Mit dem Steigungsdreieck lässt sich die Steigung berechnen:

Eine ganzrationalen Funktion zweiten Grades hat keine Wendestelle.
b)
Höhe berechnen
Die Fahrrinne ist achsensymmetrisch. Daher genügt es, zu berechnen.
zu berechnen.
 Länge der Station ermitteln
Länge der Station ermitteln
Zuerst wird der Flächeninhalt der gesamten Querschnittsfläche berechnet. Dieser setzt sich zusammen aus dem Flächeninhalt unter dem Graphen von
der gesamten Querschnittsfläche berechnet. Dieser setzt sich zusammen aus dem Flächeninhalt unter dem Graphen von  im Intervall
im Intervall  bis
bis  sowie den Flächeninhalten der Trapeze auf beiden Seiten.
sowie den Flächeninhalten der Trapeze auf beiden Seiten.
 umgeformt ergibt
umgeformt ergibt  Die Länge entspricht folglich
Die Länge entspricht folglich  .
.
Die Fahrrinne ist achsensymmetrisch. Daher genügt es,
Zuerst wird der Flächeninhalt
c)
Die Kosinusfunktion  ist symmetrisch zur
ist symmetrisch zur  -Achse. Daher wird von einer Kosinusfunktion ausgegangen.
Die allgemeine Funktionsgleichung der Kosinusfunktion lautet:
-Achse. Daher wird von einer Kosinusfunktion ausgegangen.
Die allgemeine Funktionsgleichung der Kosinusfunktion lautet:
 .
Zunächst folgt aus der Achsensymmetrie zur
.
Zunächst folgt aus der Achsensymmetrie zur  -Achse, dass
-Achse, dass  ist.
ist.
Für die Periode gilt allgemein: Der Abstand zwischen zwei Hochpunkten beträgt
Der Abstand zwischen zwei Hochpunkten beträgt  also gilt
also gilt  Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{rll}
p&=&\dfrac{2\cdot\pi}{b} \\[5pt]
16&=&\dfrac{2\cdot\pi}{b} \quad \scriptsize \mid\;\cdot b\;\mid\;:16 \\[5pt]
b&=&\dfrac{2\cdot\pi}{16}=\dfrac{\pi}{8}
\end{array}\)](https://mathjax.schullv.de/5b8ebdd775655ca316f5c5ef647780033c2d37ea8cc0655ae397976679532c22?color=5a5a5a) Die Amplitude beträgt
Die Amplitude beträgt  und die Verschiebung in
und die Verschiebung in  -Richtung
-Richtung  .
Dazu kommt, dass der Funktionsgraph an der
.
Dazu kommt, dass der Funktionsgraph an der  -Achse gespiegelt wurde, wodurch die Funktionsgleichung vor dem vertikalen Verschieben um
-Achse gespiegelt wurde, wodurch die Funktionsgleichung vor dem vertikalen Verschieben um  mit
mit  multipliziert wird.
Folglich kann eine mögliche Funktion
multipliziert wird.
Folglich kann eine mögliche Funktion  lauten.
lauten.
Für die Periode gilt allgemein:
Lösung A 2.2
a)
Zeigen, dass das Zylindervolumen unabhängig von  ist
Das Volumen eines Zylinders wird berechnet über
ist
Das Volumen eines Zylinders wird berechnet über 
 entspricht dem Radius
entspricht dem Radius  und
und  entspricht der Höhe
entspricht der Höhe 
![\(\begin{array}[t]{rll}
V&=&\pi \cdot u^2 \cdot (4-f(u))\\[5pt]
&=&\pi \cdot u^2 \cdot \left(4-\left(4-\dfrac{4}{u^2}\right)\right) \\[5pt]
&=&\pi \cdot u^2 \cdot \dfrac{4}{u^2} \\[5pt]
V&=&4 \pi
\end{array}\)](https://mathjax.schullv.de/fc77b8b5ea62f23eab6bc0c22316c603c70f0117377d8a7dc2934a64cad4bf16?color=5a5a5a) Damit ist das Zylindervolumen unabhängig von
Damit ist das Zylindervolumen unabhängig von  .
.
Der Mantelflächeninhalt eines Zylinders wird berechnet über
b)
Das Dreieck ist genau dann gleichschenklig, wenn die Steigung der Tangente im Punkt  gleich
gleich  ist.
ist.

 Gleichsetzen der Ableitungsfunktion mit der Steigung
Gleichsetzen der Ableitungsfunktion mit der Steigung  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
\dfrac{8}{x^3}&=&1&\quad \scriptsize \mid\,\cdot x^3\; \\[5pt]
8&=& x^3&\quad \scriptsize \mid 3\sqrt\; \\[5pt]
2&=&x
\end{array}\)](https://mathjax.schullv.de/c42bf89c4e72c26e705827f7c27f2cfc43e61947f35a147fd09d336953d4e11a?color=5a5a5a) Die
Die  -Koordinate lautet
-Koordinate lautet 
c)
Die Funktion  lässt sich zunächst mit dem Faktor
lässt sich zunächst mit dem Faktor  multiplizieren.
multiplizieren.
 Damit die Funktionsterme gleich sind, muss der Faktor
Damit die Funktionsterme gleich sind, muss der Faktor  noch gekürzt werden. Deshalb wird
noch gekürzt werden. Deshalb wird  mit
mit  ersetzt.
ersetzt.
 Die Streckfaktoren sind also in
Die Streckfaktoren sind also in  -Richtung der Faktor
-Richtung der Faktor  und in
und in  -Richtung der Faktor
-Richtung der Faktor 