Wahlteil A2

Aufgabe A2.1

Die Funktion $f$ beschreibt für $0\leq t \leq 8$ modellhaft die Wachstumsgeschwindigkeit eines Apfelbaums, der zu Beobachtungsbeginn $0,8 \, \text{m}$ hoch ist ( $t$ in Jahren nach Beobachtungsbeginn, $f(t)$ in Meter pro Jahr).

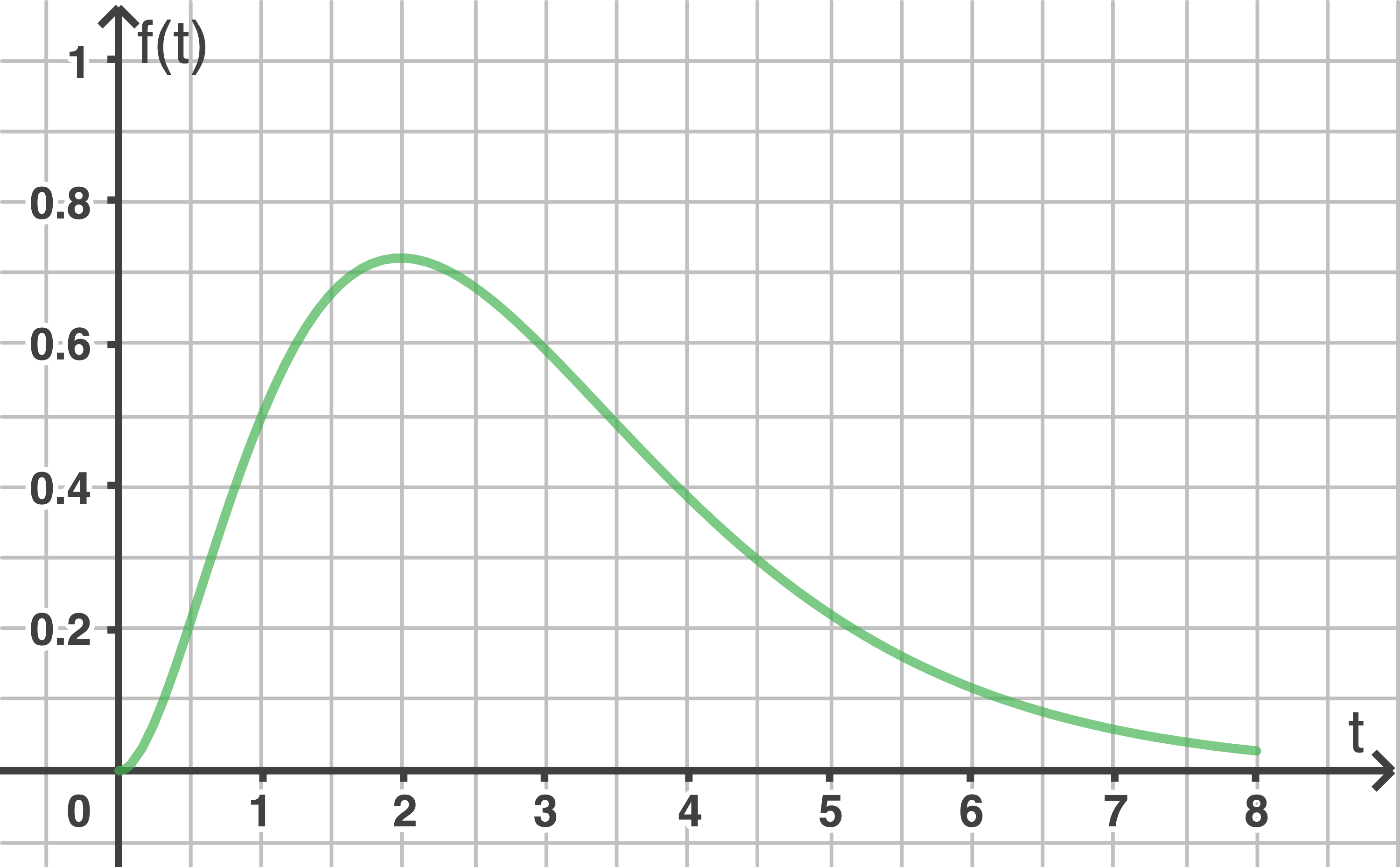
Ein Diagramm zeigt eine grüne Kurve, die eine Funktion f(t) über der Zeit t darstellt.

Die Abbildung zeigt den Graphen $G_f$ von $f.$

Bestimme die Länge des Zeitraums, in dem die Wachstumsgeschwindigkeit des Apfelbaums größer als $0,5$ Meter pro Jahr ist.

(1 VP)

Bestimme die Höhe des Apfelbaums zwei Jahre nach Beobachtungsbeginn.

(2 VP)

Die Wachstumsgeschwindigkeit eines Birnbaums, der zu Beobachtungsbeginn $1,2 \,\text{m}$ hoch ist, wird für $0 \leq t \leq 8$ modellhaft beschrieben durch die Funktion $g$ mit

$g(t)=t^2 \cdot \mathrm e^{-t}$

( $t$ in Jahren nach Beobachtungsbeginn, $g(t)$ in Meter pro Jahr).
Für die Ableitungen der Funktion $g$ gilt:

$\(\begin{array}[t]{rll} g$

Berechne den Zeitpunkt, zu dem die Wachstumsgeschwindigkeit des Birnbaums am größten ist, und gib diese Wachstumsgeschwindigkeit an.

(2 VP)

Begründe, dass der Birnbaum ab diesem Zeitpunkt weiterhin wächst, die Wachstumsgeschwindigkeit jedoch ständig abnimmt.

(2 VP)

Formuliere eine Frage im Sachzusammenhang, die auf die Gleichung $\dfrac{1}{5} \displaystyle\int_{x}^{x+5}g(t)\;\mathrm dt =0,3$ führt.

(1,5 VP)

Zeige, dass für $0\leq t \leq8$ die Funktion $h$ mit

$h(t)=(-t^2-2t-2)\cdot\mathrm e^{-t} +3,2$

die Höhe des Birnbaums beschreibt ( $t$ in Jahren nach Beobachtungsbeginn, $h(t)$ in Meter).

(2 VP)

Durch die Zugabe eines Düngers wird das Wachstum von Birnbäumen beeinflusst. Die Höhe eines gedüngten Birnbaums wird durch die Funktion $k$ beschrieben mit

$k(t)=-2,3\cdot\mathrm e^{-t} +3,5$

( $t\geq0$ in Jahren nach Beobachtungsbeginn, $k(t)$ in Meter).
Die Höhe eines ungedüngten Birnbaums wird weiterhin durch die Funktion $h$ beschrieben. Beide Birnbäume haben zu Beobachtungsbeginn dieselbe Höhe.
Berechne den Zeitpunkt, bis zu dem die Wachstumsgeschwindigkeit des gedüngten Birnbaums größer ist als die des ungedüngten Birnbaums.

(2 VP)

Untersuche rechnerisch, welcher der beiden Bäume zuerst eine Höhe von $3,1 \,\text{m}$ erreicht.

(1,5 VP)

Aufgabe A2.2

Für jedes $t\gt 0$ ist eine Funktion $f_t$ gegeben durch $f_t(x)=-4x^3+12tx^2.$

Bestimme die Nullstellen von $f_t$ .

(1 VP)

Der Graph von $f_t$ schließt mit der $x$ -Achse eine Fläche mit dem Inhalt $A_t$ ein.
Ermittle denjenigen Wert von $t,$ für den $A_t=\dfrac{16}{3}$ gilt.

(2,5 VP)

Für $t=\dfrac{2}{3}$ gibt es Tangenten an den Graphen von $f_t$ , die den Punkt $S(3\mid 0)$ enthalten.
Berechne die $x-$ Koordinaten der zugehörigen Berührpunkte.

(2,5 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung A2.1

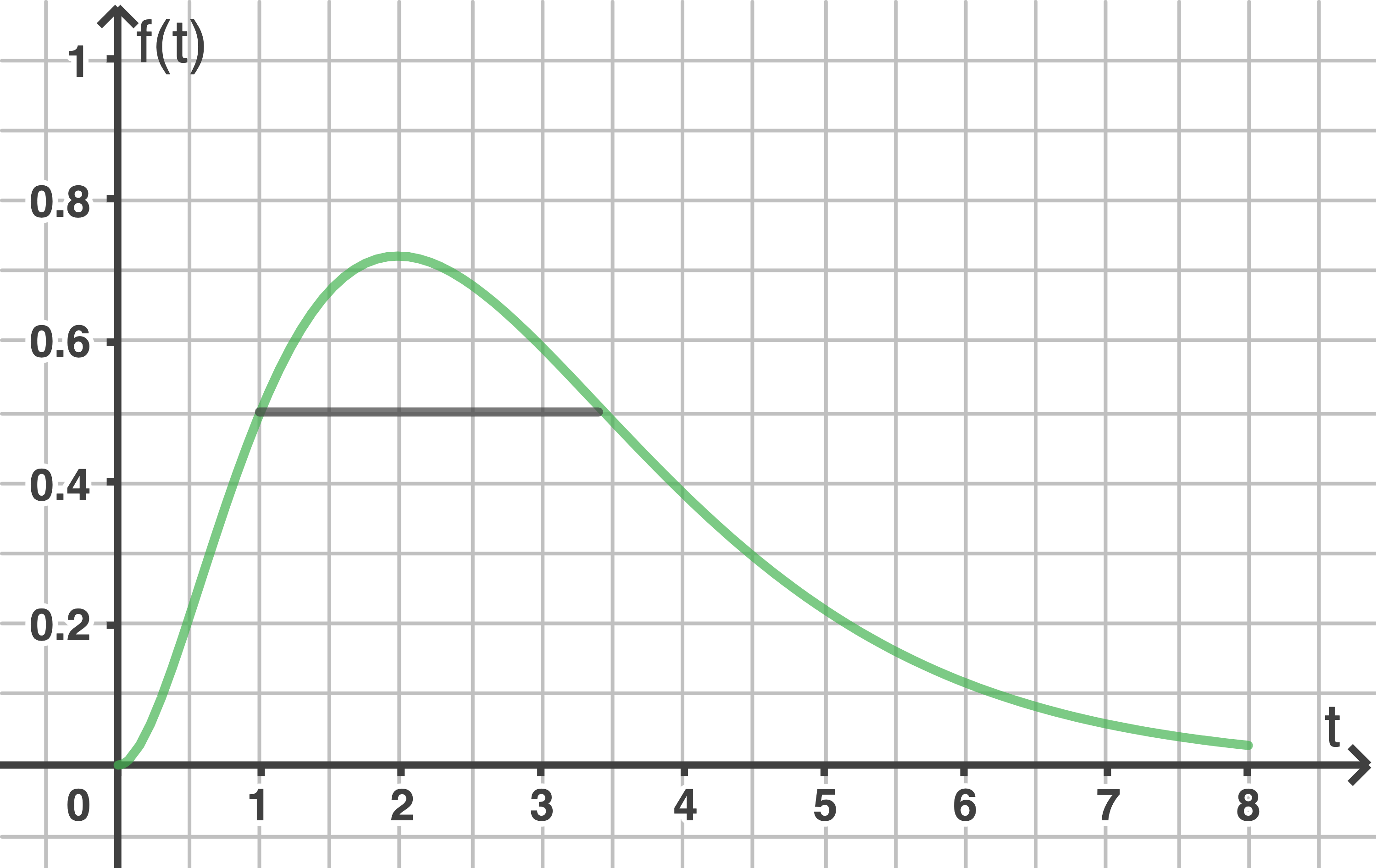
Graf einer Funktion f(t) mit einer Kurve, die einen Höchstpunkt und anschließenden Abfall zeigt.

Der Zeitraum beträgt etwa 2,4 Jahre, in dem der Apfelbaum schneller als 0,5 m pro Jahr wächst.

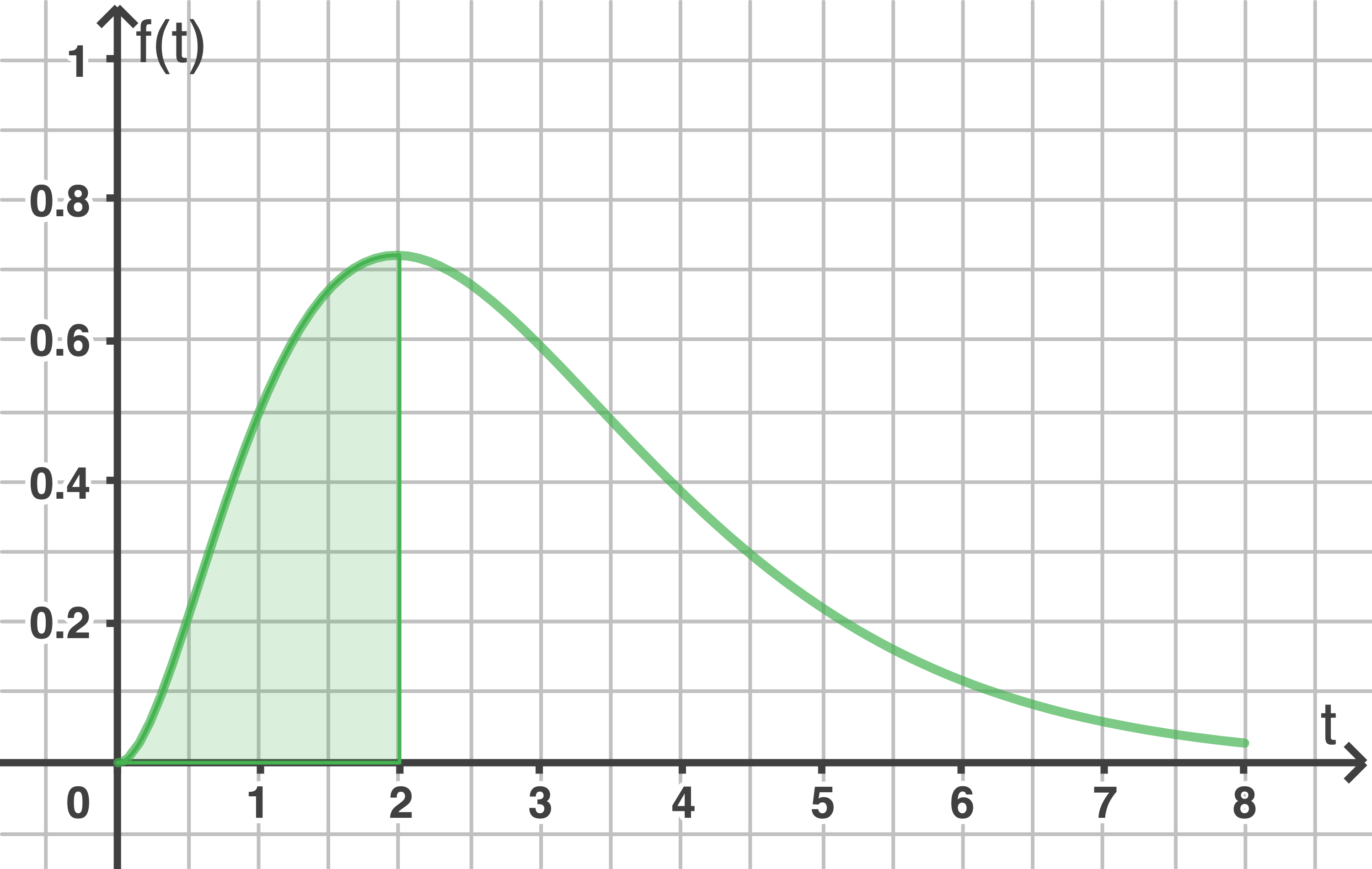
Graph einer Funktion f(t) mit Achsenbeschriftung und einem schattierten Bereich.

Um die Höhe des Baums nach 2 Jahren zu bestimmen, wird die Fläche, die der Graph der Funktion und die $x$ -Achse im Intervall $[0;2]$ einschließt, betrachtet. Es sind ca. 17 Kästchen, d.h. $17 \cdot 0,5 \cdot 0,1= 0,85.$ Da der Baum zu Beobachtungsbeginn $0,8\,\text{m}$ hoch ist hat er nach 2 Jahren somit eine Höhe von ca. $1,65 \;\text{m}.$

Maximale Wachstumsgeschwindigkeit
Mit dem notwendigen Kriterium für Extremstellen von $g$ gilt:

$\(\begin{array}[t]{rll} 0&=& g$

Mit dem hinreichenden Kriterium für Extremstellen folgt:

$\(g$ $= 2e^{-0} -4\cdot 0 \cdot \mathrm e^{ -0}+0^2\cdot \mathrm e^{-0}$ $=2 \gt 0$

$\(g$ $= 2e^{-2} -4\cdot 2 \cdot \mathrm e^{-2}+2^2\cdot \mathrm e^{-2}$ $=-2\cdot \mathrm e^{-2} \lt 0$

Ein Vergleich der Funktionswerte an den Intervallrändern ergibt:

$g(2) = 2^2 \cdot \mathrm e^{-2} \approx 0,54$

$g(0) = 0^2 \cdot \mathrm e^{-0} = 0$

$g(8) = 8^2 \cdot \mathrm e^{-8} \approx 0,02$

Also ist $g(2) \gt g(0)$ und $g(2)\gt g(8).$

Die Wachstumsgeschwindigkeit ist nach zwei Jahren mit ca. $54\,\text{ cm}$ pro Jahr am größten.

Begründung
Der Baum wächst weiter wegen $g(t) =t^2\cdot \mathrm e^{-t} \gt 0$ für $t \gt2.$

Es gilt $\(g$ für $t\gt2$ und deshalb nimmt die Wachstumsgeschwindigkeit ab.

Frage
Wann beginnt ein Zeitraum von fünf Jahren, in dem der Baum durchschnittlich $30 \,\text{cm}$ pro Jahr wächst?

Für die Funktion $h$ gilt: $h(0)=-2+3,2=1,2.$
Dies entspricht der Höhe des Birnbaums zu Beobachtungsbeginn und außerdem gilt:

$\(\begin{array}[t]{rll} &h$

Da $g$ die erste Ableitung von $h$ ist und die Anfangshöhe übereinstimmt, beschreibt $h$ damit insgesamt die Höhe des Birnbaums.

Zeitpunkt
$\(k$

$\(\begin{array}[t]{rll} k$

Die Lösung der Ungleichung ist $-\sqrt{2,3} \lt t \lt \sqrt{2,3} \approx 1,5.$

Der gedüngte Baum wächst folglich ca. die ersten 1,5 Jahre schneller als der ungedüngte Baum.

Höhe
Gedüngter Baum: $k(t)=3,1$ ergibt $t_3= -\ln \left(\dfrac{0,4}{2,3} \right)\approx 1,75$

Ungedüngter Baum: $h(t_3)\approx 1,71 \lt 3,1.$

Der gedüngte Baum erreicht die Höhe von 3,1 Metern zuerst.

Lösung A2.2

$\begin{array}[t]{rll} f_t(x)&=& 0 \\[5pt] -4x^3+12tx^2 &=& 0\\[5pt] -4x^2\cdot (x-3t) &=& 0\\[5pt] \end{array}$

Die Nullstellen liegen bei $x_1=0$ und $x_2=3t.$

Wert von t
Für den Inhalt der Fläche, die der Graph von $f_t$ mit der $x$ -Achse einschließt folgt in Abhängigkeit von $t:$

$A_t= \displaystyle\int_{0}^{3t}f_t(x)\;\mathrm dx$ $= \left[ -x^4+4tx^3 \right]_0^{3t}= 27t^4$

Gleichsetzen liefert:

$\begin{array}[t]{rll} 27t^4&=&\dfrac{16}{3} &\quad \scriptsize \mid\;:27 \; \mid 4\sqrt{\;} \\[5pt] t&=&\pm\dfrac{2}{3} \end{array}$

Die passende Lösung ist hier nur $t_1 = \dfrac{2}{3}$ , da $t \gt 0.$

Die Funktion $f_{\frac{2}{3}}$ wird abgeleitet und die Tangentengleichung aufgestellt.

$\(\begin{array}[t]{rll} f_{\frac{2}{3}}&=&-4x^3 +8x^2 \\[5pt] f$

Die $x$ -Koordinaten der Berührpunkte werden mit $u$ bezeichnet.
Die Tangentengleichung lautet

$y_t=(-12u^2 +16u) \cdot (x-u)-4u^3 +8u^2$

Die Punktprobe mit $S(3 \mid 0)$ ergibt:

Vollständigen Rechenweg anzeigen

$0 =4u \cdot(2u^2-11u+12)$

Nach $u$ aufgelöst ergeben sich $u_1=0, u_2=\dfrac{3}{2}, u_3=4$ , welches die $x$ -Koordinaten der Berührpunkte sind.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?