Wahlteil B1
Aufgabe B1.1
Gegeben sind die Punkte  ,
,  ,
,  und
und  .
.
Das Quadrat ist die Grundfläche einer Pyramide mit der Spitze
ist die Grundfläche einer Pyramide mit der Spitze  .
.
Das Quadrat
a)
Die Seitenfläche  liegt in der Ebene
liegt in der Ebene  .
Bestimme eine Koordinatengleichung von
.
Bestimme eine Koordinatengleichung von  .
Berechne den Winkel, der von der Seitenfläche
.
Berechne den Winkel, der von der Seitenfläche  und der Grundfläche der Pyramide eingeschlossen wird.
Berechne den Flächeninhalt des Dreiecks
und der Grundfläche der Pyramide eingeschlossen wird.
Berechne den Flächeninhalt des Dreiecks  .
.
(4 VP)
b)
Betrachtet werden nun Quader, die jeweils vier Eckpunkte auf den Pyramidenkanten und vier Eckpunkte in der Grundfläche der Pyramide haben.
Einer dieser Quader hat den Eckpunkt .
Berechne sein Volumen.
Bei einem anderen dieser Quader handelt es sich um einen Würfel.
Welche Koordinaten hat dessen Eckpunkt auf der Kante
.
Berechne sein Volumen.
Bei einem anderen dieser Quader handelt es sich um einen Würfel.
Welche Koordinaten hat dessen Eckpunkt auf der Kante  ?
?
Einer dieser Quader hat den Eckpunkt
(4 VP)
Aufgabe B1.2
In einem Gefäß  sind
sind  schwarze und
schwarze und  weiße Kugeln.
weiße Kugeln.
In einem Gefäß sind
sind  schwarze und
schwarze und  weiße Kugeln.
weiße Kugeln.
In einem Gefäß
a)
Aus Gefäß  wird
wird  Mal eine Kugel mit Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit, dass mindestens
Mal eine Kugel mit Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit, dass mindestens  Mal eine schwarze Kugel gezogen wird.
Aus Gefäß
Mal eine schwarze Kugel gezogen wird.
Aus Gefäß  wird
wird  Mal eine Kugel mit Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit, dass genau
Mal eine Kugel mit Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit, dass genau  schwarze Kugeln gezogen werden, und zwar bei direkt aufeinander folgenden Zügen.
schwarze Kugeln gezogen werden, und zwar bei direkt aufeinander folgenden Zügen.
(4 VP)
b)
Nun werden aus  zwei Kugeln ohne Zurücklegen gezogen und in das Gefäß
zwei Kugeln ohne Zurücklegen gezogen und in das Gefäß  gelegt. Anschließend wird eine Kugel aus
gelegt. Anschließend wird eine Kugel aus  gezogen.
Mit welcher Wahrscheinlichkeit ist diese Kugel schwarz?
gezogen.
Mit welcher Wahrscheinlichkeit ist diese Kugel schwarz?
(3 VP)
Lösung B1.1
a)  Bestimmen einer Koordinatengleichung für Ebene
Der Aufgabenstellung kannst du entnehmen, dass das Quadrat
Bestimmen einer Koordinatengleichung für Ebene
Der Aufgabenstellung kannst du entnehmen, dass das Quadrat  die Grundfläche einer Pyramide mit der Spitze
die Grundfläche einer Pyramide mit der Spitze  ist. Weiterhin weißt du, dass die Seitenfläche
ist. Weiterhin weißt du, dass die Seitenfläche  in der Ebene
in der Ebene  liegt. Deine Aufgabe ist es dabei, eine Koordinatengleichung der Ebene
liegt. Deine Aufgabe ist es dabei, eine Koordinatengleichung der Ebene  zu bestimmen. Die Koordinatengleichung einer Ebene baut sich dabei wie folgt auf:
zu bestimmen. Die Koordinatengleichung einer Ebene baut sich dabei wie folgt auf:
 mit:
mit:
 bestimmen, so bestimmst du zunächst den Normalenvektor
bestimmen, so bestimmst du zunächst den Normalenvektor  über das Vektorprodukt bzw. Kreuzprodukt. Verwende dazu die Information, dass die Seitenfläche
über das Vektorprodukt bzw. Kreuzprodukt. Verwende dazu die Information, dass die Seitenfläche  der Pyramide in der Ebene
der Pyramide in der Ebene  liegt.
liegt.





 .
.
 Bestimmen des Winkels zwischen den Flächen
Bestimmen des Winkels zwischen den Flächen  und
und  Nun ist es deine Aufgabe, den Winkel
Nun ist es deine Aufgabe, den Winkel  zwischen Seitenfläche
zwischen Seitenfläche  und Grundfläche
und Grundfläche  der Pyramide zu berechnen. Hier gilt es also einen Winkel zwischen zwei Ebenen zu berechnen. Einen Winkel zwischen zwei gegebenen Ebenen berechnest du dabei über folgende Formel:
der Pyramide zu berechnen. Hier gilt es also einen Winkel zwischen zwei Ebenen zu berechnen. Einen Winkel zwischen zwei gegebenen Ebenen berechnest du dabei über folgende Formel:
 mit:
mit:
 der Ebene, in welcher die Grundfläche
der Ebene, in welcher die Grundfläche  liegt, könntest du wie oben über das Kreuzprodukt bestimmen. Vergleichst du jedoch die Variablen der Punkte
liegt, könntest du wie oben über das Kreuzprodukt bestimmen. Vergleichst du jedoch die Variablen der Punkte  ,
,  ,
,  und
und  , mit
, mit
 -Ebene liegen (
-Ebene liegen ( -Koordinate ist überall Null). Ein Vektor, welcher senkrecht auf der Ebene steht, in welcher sich auch die Grundfläche
-Koordinate ist überall Null). Ein Vektor, welcher senkrecht auf der Ebene steht, in welcher sich auch die Grundfläche  befindet, zeigt also in Richtung der
befindet, zeigt also in Richtung der  -Achse. Für den Normalenvektor
-Achse. Für den Normalenvektor  gilt hier also:
gilt hier also:

 Berechnen des Flächeninhalts des Dreiecks
Berechnen des Flächeninhalts des Dreiecks  Zuletzt sollst den Flächeninhalt
Zuletzt sollst den Flächeninhalt  des Dreiecks
des Dreiecks  berechnen. Der Flächeninhalt eines Dreiecks berechnet sich dabei über folgenden Zusammenhang:
berechnen. Der Flächeninhalt eines Dreiecks berechnet sich dabei über folgenden Zusammenhang:
 mit:
mit:




und
: Einträge des Normalenvektors
der Ebene
: Über Punktprobe zu bestimmende Konstante
Hast du den Normalenvektor  der Ebene
der Ebene  bestimmt, so bestimmst du über eine Punktprobe die Konstante
bestimmt, so bestimmst du über eine Punktprobe die Konstante  . Verwende dazu die Koordinaten von Punkt
. Verwende dazu die Koordinaten von Punkt  ,
,  oder
oder  .
.
1. Schritt: Bestimmen des Normalenvektors  über das Vektorprodukt
über das Vektorprodukt
Willst du den Normalenvektor  bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene
bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene  aufspannen. Da die Seitenfläche
aufspannen. Da die Seitenfläche  in der Ebene
in der Ebene  liegt, kannst du hier die Vektoren
liegt, kannst du hier die Vektoren  und
und  verwenden:
verwenden:
Berechne nun wie folgt das Vektorprodukt bzw. Kreuzprodukt der Vektoren  und
und  , um den Normalenvektor
, um den Normalenvektor  zu bestimmen:
zu bestimmen:
Da beim Normalenvektor  nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor  in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante  bestimmst du hier nun, indem du beispielsweise die Koordinaten von
bestimmst du hier nun, indem du beispielsweise die Koordinaten von  mit
mit  für
für  ,
,  und
und  einsetzt und die Gleichung nach
einsetzt und die Gleichung nach  löst:
löst:
Eine Koordinatengleichung der Ebene  lautet also:
lautet also:
: Winkel zwischen den Ebenen
: Normalenvektoren der Ebenen
Willst du also den Winkel  zwischen der Seitenfläche
zwischen der Seitenfläche  und der Grundfläche
und der Grundfläche  berechnen, so benötigst du hier die Normalenvektoren dieser Ebenen. Den Normalenvektor der Ebene
berechnen, so benötigst du hier die Normalenvektoren dieser Ebenen. Den Normalenvektor der Ebene  , in welcher die Seitenfläche
, in welcher die Seitenfläche  liegt, hast du oben schon bestimmt. Der Normalenvektor der Ebene, in welcher die Grundfläche
liegt, hast du oben schon bestimmt. Der Normalenvektor der Ebene, in welcher die Grundfläche  liegt, gilt es noch zu berechnen.
liegt, gilt es noch zu berechnen.
1. Schritt: Bestimmen des gesuchten Normalenvektors
Den Normalenvektor
2. Schritt: Bestimmen des Winkels  Den Winkel
Den Winkel  bestimmst du nun, in dem du
bestimmst du nun, in dem du  und
und  in den oben gezeigten Zusammenhang einsetzt und wie folgt berechnest:
in den oben gezeigten Zusammenhang einsetzt und wie folgt berechnest:
![\( \scriptsize\begin{array}{rll}
\cos(\alpha)&=&\dfrac{\overrightarrow{n_E} \cdot \overrightarrow{n_{ABCD}}}{|\overrightarrow{n_E}| \cdot |\overrightarrow{n_{ABCD}}|} \\
&=&\dfrac{\begin{pmatrix}0 \\ 12 \\ 5\end{pmatrix} \cdot
\begin{pmatrix}0\\0\\1\end{pmatrix}}{\left|\begin{pmatrix}0 \\ 12 \\ 5\end{pmatrix}\right|
\cdot \left|\begin{pmatrix}0 \\ 0 \\ 1\end{pmatrix}\right|}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b9d16f43d40480e2c991554516b7480bc6434bb76b574dbfa0ab6dbdcff3d3a6?color=5a5a5a)
![\( \scriptsize\begin{array}{rll}
\cos(\alpha)
&=&\dfrac{0 \cdot 0 + 12 \cdot 0 + 5 \cdot 1}{\sqrt{0^2 + 12^2 + 5^2} \cdot \sqrt{0^2 + 0^2 + 1^2}}\; \\
&=&\;\dfrac{5}{\sqrt{169} \cdot \sqrt{1}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cbb02dff0ad24f6e1a985cba931c9e58c956b9326f420a8f354f5da74c29e92f?color=5a5a5a)
![\( \scriptsize\begin{array}{rll}
\cos{\alpha}&=&\dfrac{5}{13}&\scriptsize \mid\;\cos^{-1}\\[5pt]
\alpha&=&\cos^{-1}(\frac{5}{13})\;=\;67,38\,\text{°}
\end{array}\)](https://mathjax.schullv.de/7c01514c91bf8935fa2489646b77abb87a45531bad867e75eca4e228f75d3680?color=5a5a5a)
Der Winkel zwischen der Seitenfläche  und der Grundfläche
und der Grundfläche  beträgt also 67,38°.
beträgt also 67,38°.
: Grundseite
: Höhe des Dreiecks
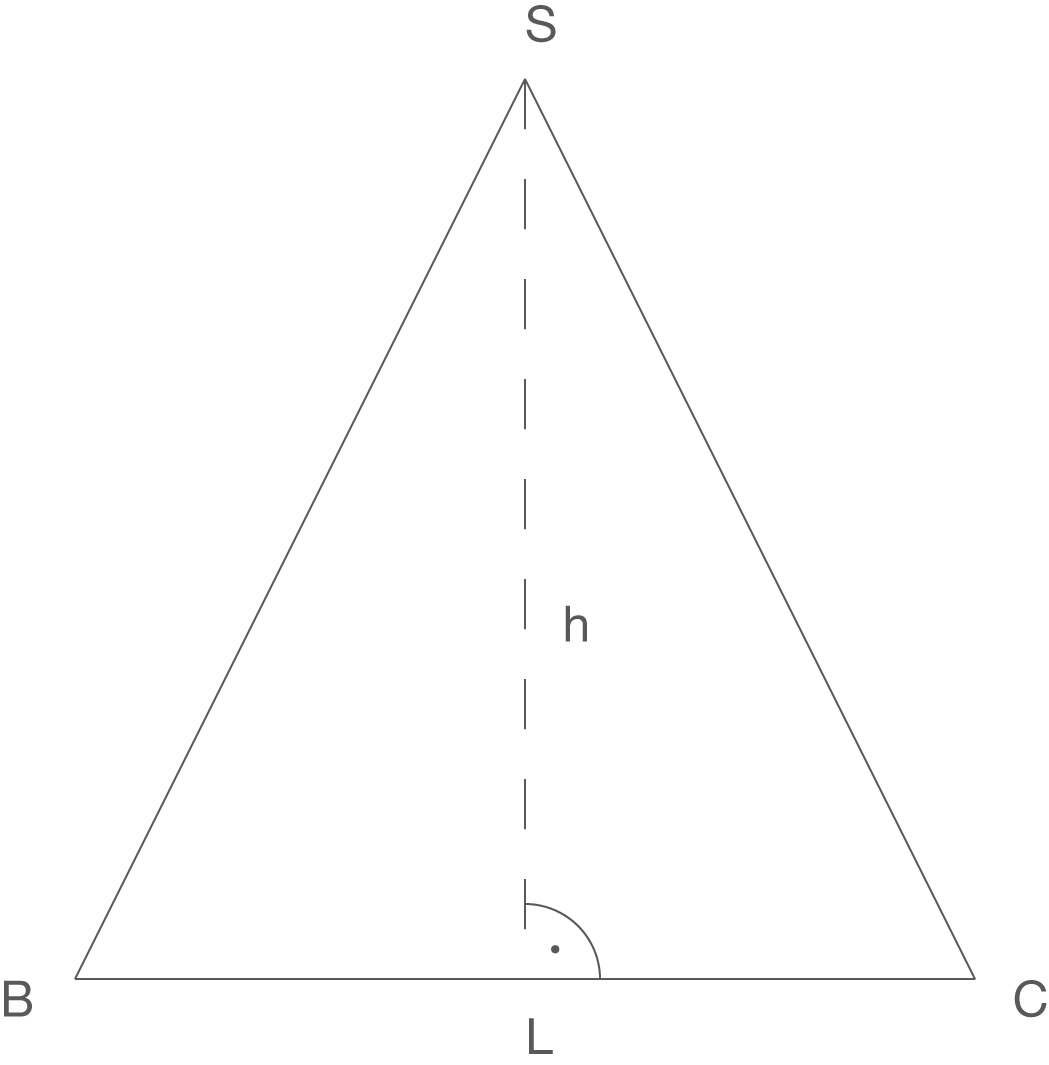
Fertige dir eine Skizze des Dreiecks  an, um dir das Lösen dieser Aufgabe einfacher zu gestalten:
an, um dir das Lösen dieser Aufgabe einfacher zu gestalten:

Willst du hier den Flächeninhalt  des Dreiecks
des Dreiecks  bestimmen, so musst du die Länge der Höhe
bestimmen, so musst du die Länge der Höhe  berechnen. Diese Länge ermittelst du, in dem du zunächst die Länge der Strecke
berechnen. Diese Länge ermittelst du, in dem du zunächst die Länge der Strecke  berechnest. Zeichnest du die Seitenansicht der Pyramide
berechnest. Zeichnest du die Seitenansicht der Pyramide  , so kannst du erkennen, dass die Strecke
, so kannst du erkennen, dass die Strecke  eine der Seitenlängen der Pyramiden entspricht:
eine der Seitenlängen der Pyramiden entspricht:

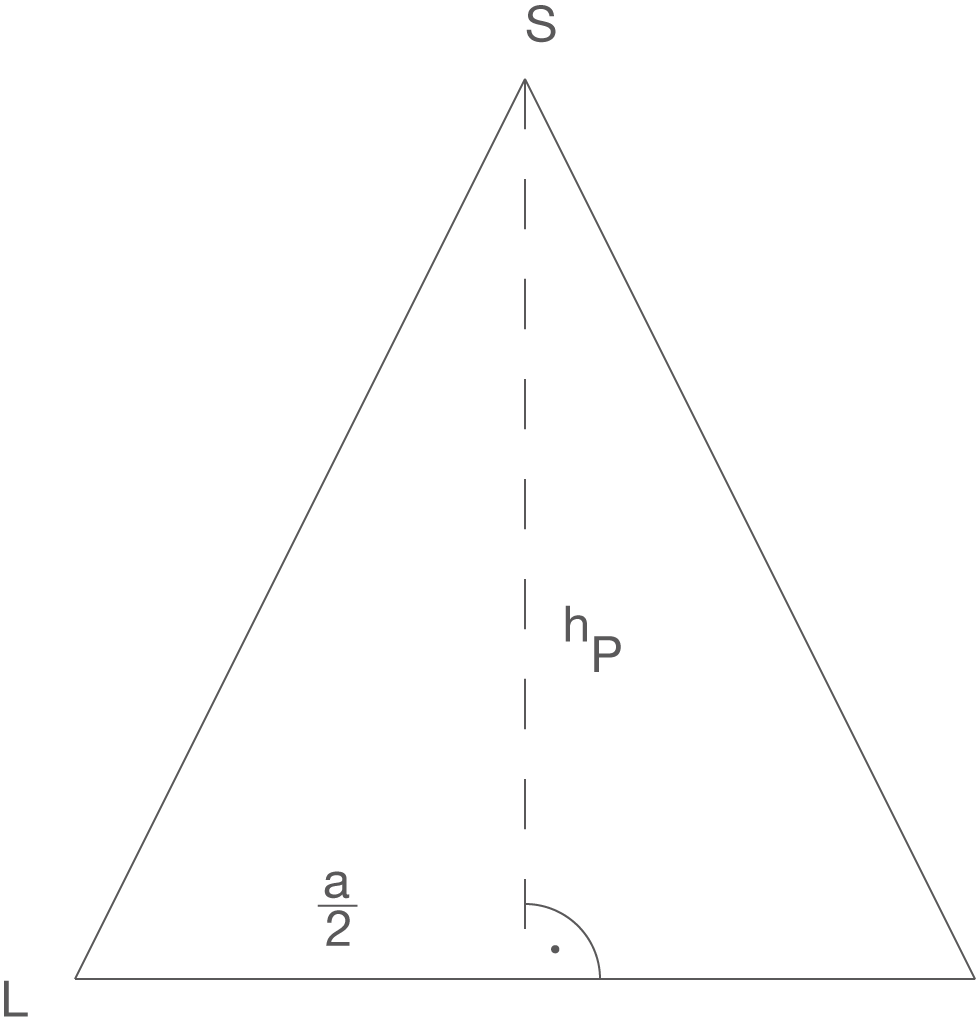
Betrachtest du die Skizze oben näher, so kannst du weiterhin erkennen, dass die Strecke  mit der Höhe
mit der Höhe  der Pyramide und der Hälfte der Grundseitenlänge
der Pyramide und der Hälfte der Grundseitenlänge  in einem rechtwinkligen Dreieck liegt. Diese lässt sich also über den Satz des Pythagoras in diesem Dreieck bestimmen.
in einem rechtwinkligen Dreieck liegt. Diese lässt sich also über den Satz des Pythagoras in diesem Dreieck bestimmen.
Gehe beim Berechnen des Flächeninhalts  also so vor:
also so vor:
- Bestimme die Höhe
der Pyramide
- Bestimme die Grundseitenlänge
- Berechne die Länge der Strecke
- Berechne den Flächeninhalt
1. Schritt: Bestimmen von  und
und  Die Höhe der Pyramide
Die Höhe der Pyramide  ergibt sich aus der
ergibt sich aus der  -Koordinaten der Spitze
-Koordinaten der Spitze  der Pyramide:
der Pyramide:
Die Grundseiten Länge entspricht beispielsweise der Länge des Vektors  , da dieser Vektor eine der Quadratseiten des Quadrates
, da dieser Vektor eine der Quadratseiten des Quadrates  beschreibt:
beschreibt:
2. Schritt: Bestimmen der Länge der Strecke  Betrachtest du die Skizze oben näher, so kannst du erkennen, dass
Betrachtest du die Skizze oben näher, so kannst du erkennen, dass  und
und  die Katheten des betrachteten rechtwinkligen Dreiecks sind. Willst du die Länge der Strecke
die Katheten des betrachteten rechtwinkligen Dreiecks sind. Willst du die Länge der Strecke  über den Satz des Pythagroas bestimmen, so gehst du hier also so vor:
über den Satz des Pythagroas bestimmen, so gehst du hier also so vor:
Setzt du nun  sowie
sowie  in die oben gezeigte Formel für den Flächeninhalt des Dreicks
in die oben gezeigte Formel für den Flächeninhalt des Dreicks  ein, so ergibt sich dieser wie folgt:
ein, so ergibt sich dieser wie folgt:
Der Flächeninhalt des Dreiecks  ist 65 FE.
ist 65 FE.
b)  Berechnen des Quadervolumens
Der Aufgabenstellung kannst du nun entnehmen, dass nun Quader betrachtet werden, die jeweils vier Eckpunkte auf den Pyramidenkanten und vier Eckpunkte in der Grundfläche der Pyramide haben. Einer dieser Quader hat nun den Eckpunkt
Berechnen des Quadervolumens
Der Aufgabenstellung kannst du nun entnehmen, dass nun Quader betrachtet werden, die jeweils vier Eckpunkte auf den Pyramidenkanten und vier Eckpunkte in der Grundfläche der Pyramide haben. Einer dieser Quader hat nun den Eckpunkt  .
.
Deine Aufgabe ist es nun, das Volumen dieses Quaders zu berechnen. Das Volumen eines Quaders ergibt sich dabei über folgende Formel:
eines Quaders ergibt sich dabei über folgende Formel:
 mit:
mit:
 berechnest du hier, indem du zunächst die Gerade
berechnest du hier, indem du zunächst die Gerade  definierst, auf welcher die Strecke
definierst, auf welcher die Strecke  liegt. Verwende dazu den Ortsvektor
liegt. Verwende dazu den Ortsvektor  von Punkt
von Punkt  als Stütz- und den Vektor
als Stütz- und den Vektor  als Richtungsvektor:
als Richtungsvektor:

![\( \begin{array}{rll}
\overrightarrow{OR}&=& \overrightarrow{x_g}\\[5pt]
\begin{pmatrix}2,5\\2,5\\z\end{pmatrix}&=& \begin{pmatrix}5 \\ 5 \\ 0\end{pmatrix} + t \cdot \begin{pmatrix}-5 \\ -5 \\ 12\end{pmatrix}\\
\end{array}\)](https://mathjax.schullv.de/6f4f2cbdd5eaf2d58b4ee69e38f28a4e5d43788ca547a7bd924f715af8eb3287?color=5a5a5a)
 Berechnen der Koordinaten des Eckpunktes
Nun soll ein weiterer Quader betrachtet werden, bei dem es sich um einen Würfel handelt. Dabei sollte dir bekannt sein, dass bei einem Würfel Länge, Breite und Höhe übereinstimmen. Deine Aufgabe ist es nun die Koordinaten von dessen Eckpunkt auf der Kante
Berechnen der Koordinaten des Eckpunktes
Nun soll ein weiterer Quader betrachtet werden, bei dem es sich um einen Würfel handelt. Dabei sollte dir bekannt sein, dass bei einem Würfel Länge, Breite und Höhe übereinstimmen. Deine Aufgabe ist es nun die Koordinaten von dessen Eckpunkt auf der Kante  zu bestimmen.
zu bestimmen.
Wie oben schon beschrieben, bestimmte der Punkt unter anderem Breite und Länge des Würfels. Dabei entsprach gerade das Doppelte der
unter anderem Breite und Länge des Würfels. Dabei entsprach gerade das Doppelte der  -Koordinate der Länge und das Doppelte der
-Koordinate der Länge und das Doppelte der  -Koordinate der Breite des Würfels.
-Koordinate der Breite des Würfels.
Da der hier zu bestimmende Punkt auf der Kante
auf der Kante  liegt, werden dessen Koordinaten von Gerade
liegt, werden dessen Koordinaten von Gerade  bestimmt. Von oben weißt du, dass dessen
bestimmt. Von oben weißt du, dass dessen  - und
- und  -Koordinate mit denen von Punkt
-Koordinate mit denen von Punkt  , der unterhalb von
, der unterhalb von  liegt, übereinstimmt.
liegt, übereinstimmt.
Daraus folgt, dass die -Koordinate dem Doppelten der
-Koordinate dem Doppelten der  - und
- und  -Koordinaten von
-Koordinaten von  entsprechen muss, damit es sich beim betrachteten Quader um einen Würfel handelt.
entsprechen muss, damit es sich beim betrachteten Quader um einen Würfel handelt.
![\(\begin{array}[t]{rll}
\overrightarrow{OR_t}&=& \begin{pmatrix}5 \\ 5 \\ 0\end{pmatrix} + t \cdot \begin{pmatrix}-5 \\ -5 \\ 12\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}5 - 5 \cdot t \\ 5 - 5 \cdot t \\ 12 \cdot t\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/6cba5595dac34704175ad2e339597745520d22b584bf8ad8e96f535abc810f6f?color=5a5a5a)

![\(\begin{array}[t]{rll}
2 \cdot x_1 &=& x_3 & \\[5pt]
2 \cdot (5 - 5 \cdot t)&=& 12 \cdot t &\\[5pt]
10 - 10 \cdot t &=& 12\cdot t& \quad \scriptsize \mid +10\cdot t\\[5pt]
10 &=& 22t& \quad \scriptsize \mid :22\\[5pt]
\dfrac{5}{11}&=& t
\end{array}\)](https://mathjax.schullv.de/8646849d29fd554642d6161b2fc623e4b92decd3723797db0141c989ae5076a2?color=5a5a5a)
Deine Aufgabe ist es nun, das Volumen dieses Quaders zu berechnen. Das Volumen
: Länge des Quaders
: Breite des Quaders
: Höhe des Quaders
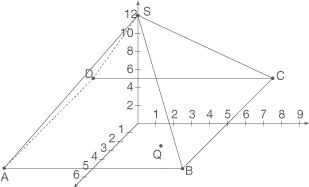
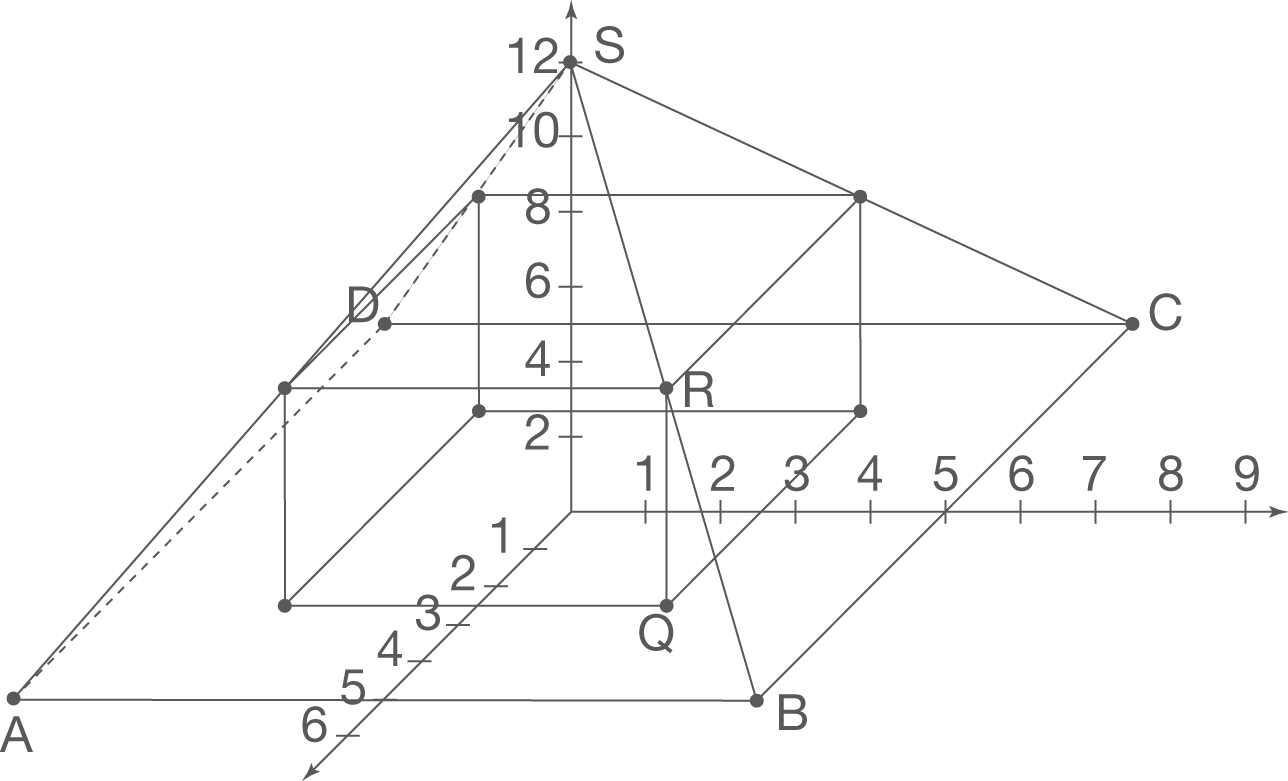
Bevor du also das Volumen des Quaders bestimmen kannst, musst du dessen Länge, Breite und Höhe bestimmen. Fertige dir dazu eine Skizze des Sachverhalts an, in welche du zunächst die Pyramide  und den Punkt
und den Punkt  einzeichnest:
einzeichnest:

Vergleichst du die Koordinaten von  und dem Punkt
und dem Punkt  , so kannst du erkennen, dass der Punkt
, so kannst du erkennen, dass der Punkt  auf dem Ortsvektor
auf dem Ortsvektor  liegt. Folglich liegt der darüberliegende Punkt
liegt. Folglich liegt der darüberliegende Punkt  des Quaders auf der Strecke
des Quaders auf der Strecke  . Willst du also die Höhe des Quaders berechnen, so bestimmst du die Länge des Vektors
. Willst du also die Höhe des Quaders berechnen, so bestimmst du die Länge des Vektors  . Berechne dazu die Koordinaten von
. Berechne dazu die Koordinaten von  über die Gerade, auf welcher die Strecke
über die Gerade, auf welcher die Strecke  liegt.
liegt.
Die Länge und die Breite des Quaders ermittelst du, indem du die relative Lage des Punktes zu den Koordinatenachsen näher betrachtest.
zu den Koordinatenachsen näher betrachtest.
Die Länge und die Breite des Quaders ermittelst du, indem du die relative Lage des Punktes
1. Schritt: Berechnen der Quaderhöhe
Die Quaderhöhe
Da der Punkt  senkrecht oberhalb des Punkte
senkrecht oberhalb des Punkte  liegt, weißt du, dass für dessen Koordinaten folgendes gelten muss:
liegt, weißt du, dass für dessen Koordinaten folgendes gelten muss:  .
.
Setzt du nun den Ortsvektor  von
von  mit der Geradengleichung von
mit der Geradengleichung von  gleich, so kannst du wie folgt die vollständigen Koordinaten von
gleich, so kannst du wie folgt die vollständigen Koordinaten von  bestimmen:
bestimmen:
Übertrage diese Gleichung wie folgt in ein Gleichungssystem, um die vollständigen Koordinaten von  zu bestimmen:
zu bestimmen:
Die vollständigen Koordinaten von Punkt  sind also:
sind also:  . Vergleichst du nun die Koordinaten von
. Vergleichst du nun die Koordinaten von  und
und  , so kannst du erkennen, dass die Höhe des Quaders offensichtlich
, so kannst du erkennen, dass die Höhe des Quaders offensichtlich  sein muss.
sein muss.
2. Schritt: Berechnen der Länge und der Breite des Quaders
Willst du die Länge und die Breite des Quaders bestimmen, so betrachtest du die Koordinaten von  .
.  hat eine
hat eine  -Koordinate von
-Koordinate von  . Das heißt der Abstand von
. Das heißt der Abstand von  zur
zur  -Achse beträgt 2,5. Da es sich um einen Quader handelt, dessen Grundfläche in der Fläche
-Achse beträgt 2,5. Da es sich um einen Quader handelt, dessen Grundfläche in der Fläche  liegt, muss für dessen Länge gelten:
liegt, muss für dessen Länge gelten:
.
.

3. Schritt: Berechnen des Quadervolumens  Das Quadervolumen
Das Quadervolumen  ergibt sich nun über den obigen Ansatz wie folgt:
ergibt sich nun über den obigen Ansatz wie folgt:
 .
Der Quader besitzt ein Volumen von 150 VE.
.
Der Quader besitzt ein Volumen von 150 VE.
Wie oben schon beschrieben, bestimmte der Punkt
Da der hier zu bestimmende Punkt
Daraus folgt, dass die
1. Schritt: Bestimmen der allgemeinen Koordinaten von  Die allgemeinen Koordinaten von
Die allgemeinen Koordinaten von  ergeben sich wie folgt aus der Gleichung von Gerade
ergeben sich wie folgt aus der Gleichung von Gerade  :
:
2. Schritt: Bestimmen der gesuchten Koordinaten von  Wie oben erwähnt, handelt es sich dann um einen Würfel, wenn die
Wie oben erwähnt, handelt es sich dann um einen Würfel, wenn die  -Koordinate von
-Koordinate von  dem Doppelten der
dem Doppelten der  - und der
- und der  -Koordinaten dieses Punktes entspricht. Berechne demnach mit
-Koordinaten dieses Punktes entspricht. Berechne demnach mit  die gesuchten Koordinaten von
die gesuchten Koordinaten von  über folgende Gleichung:
über folgende Gleichung:
Für  muss also
muss also  gelten. Für die gesuchten Koordinaten gilt also:
gelten. Für die gesuchten Koordinaten gilt also:
Die gesuchten Koordinaten des Eckpunktes auf der Kante  sind also
sind also  .
.
Lösung B1.2
a)  Wahrscheinlichkeit, dass mind. 12 Mal eine schwarze Kugel gezogen wird
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 20 Mal eine Kugel aus dem Gefäß
Wahrscheinlichkeit, dass mind. 12 Mal eine schwarze Kugel gezogen wird
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 20 Mal eine Kugel aus dem Gefäß  gezogen wird. Die Kugeln werden dabei jeweils wieder ins Gefäß zurückgelegt, weswegen es sich hier um ein Ziehen mit Zurücklegen handelt. Im Gefäß
gezogen wird. Die Kugeln werden dabei jeweils wieder ins Gefäß zurückgelegt, weswegen es sich hier um ein Ziehen mit Zurücklegen handelt. Im Gefäß  befinden sich 6 schwarze und 4 weiße Kugel. Deine Aufgabe ist es nun, die Wahrscheinlichkeit dafür zu bestimmen, dass bei 20 Zügen mindestens 12 Mal eine schwarze Kugeln gezogen wird.
befinden sich 6 schwarze und 4 weiße Kugel. Deine Aufgabe ist es nun, die Wahrscheinlichkeit dafür zu bestimmen, dass bei 20 Zügen mindestens 12 Mal eine schwarze Kugeln gezogen wird.
Willst du hier diese Wahrscheinlichkeit bestimmen, so betrachtest du zunächst die Zufallsvariable . Zufallsvariable
. Zufallsvariable  beschreibt dabei die Anzahl der gezogenen schwarzen Kugeln. Da bei diesem Zufallsversuch nur die Anzahl der gezogenen schwarzen Kugeln relevant ist und es sich um ein Ziehen mit Zurücklegen handelt, ist Zufallsvariable
beschreibt dabei die Anzahl der gezogenen schwarzen Kugeln. Da bei diesem Zufallsversuch nur die Anzahl der gezogenen schwarzen Kugeln relevant ist und es sich um ein Ziehen mit Zurücklegen handelt, ist Zufallsvariable  binomialverteilt. Da insgesamt
binomialverteilt. Da insgesamt  Mal gezogen wird ist
Mal gezogen wird ist  .
.
Wahrscheinlichkeit ergibt sich aus der Gesamtanzahl der schwarzen Kugeln unter allen Kugeln. Da hier die Wahrscheinlichkeit dafür gesucht wird, dass mindestens 12 Mal eine schwarze Kugeln gezogen wird, muss für die Zufallsvariable
ergibt sich aus der Gesamtanzahl der schwarzen Kugeln unter allen Kugeln. Da hier die Wahrscheinlichkeit dafür gesucht wird, dass mindestens 12 Mal eine schwarze Kugeln gezogen wird, muss für die Zufallsvariable  hier folgendes gelten:
hier folgendes gelten:
 .
Diese Wahrscheinlichkeit kannst du mit deinem GTR berechnen. Dazu musst du den binomCdf-Befehl verwenden. Da dieser aber nur Ausdrücke wie
.
Diese Wahrscheinlichkeit kannst du mit deinem GTR berechnen. Dazu musst du den binomCdf-Befehl verwenden. Da dieser aber nur Ausdrücke wie  berechnen kann, musst du hier zunächst wie folgt das Gegenereignis zu
berechnen kann, musst du hier zunächst wie folgt das Gegenereignis zu  bilden:
bilden:
 eine schwarze Kugel zu ziehen, die folgende ist:
eine schwarze Kugel zu ziehen, die folgende ist:
 ,
,  gilt. Wende den binomCdf-Befehl wie in den Schaubildern unten an, um hier die gesuchte Wahrscheinlichkeit zu berechnen. Greife dazu aber zunächst über 2nd
gilt. Wende den binomCdf-Befehl wie in den Schaubildern unten an, um hier die gesuchte Wahrscheinlichkeit zu berechnen. Greife dazu aber zunächst über 2nd  DISTR
DISTR  B:binomcdf( auf diesen zu.
B:binomcdf( auf diesen zu.
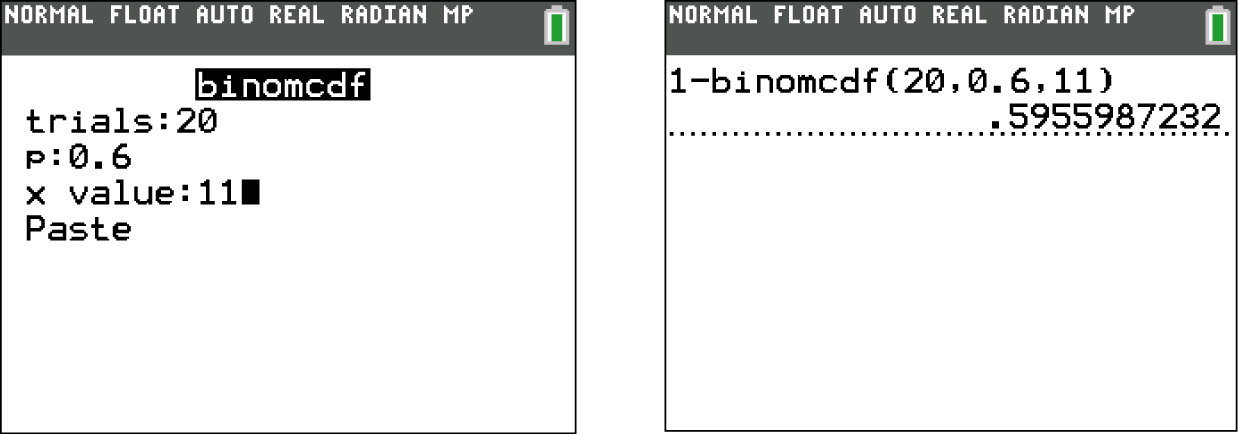 Die Wahrscheinlichkeit, mindestens 12 schwarze Kugeln aus Gefäß
Die Wahrscheinlichkeit, mindestens 12 schwarze Kugeln aus Gefäß  zu ziehen beträgt also etwa 59,6 %.
zu ziehen beträgt also etwa 59,6 %.
 Wahrscheinlichkeit, dass 2 schwarze Kugeln hintereinander gezogen werden
Nun betrachtest du Gefäß
Wahrscheinlichkeit, dass 2 schwarze Kugeln hintereinander gezogen werden
Nun betrachtest du Gefäß  , indem sich 3 schwarze und 7 weiße Kugeln befinden und aus dem mit Zurücklegen gezogen wird. Deine Aufgabe ist es dabei, die Wahrscheinlichkeit dafür zu bestimmen, dass aus diesem Gefäß genau 2 schwarze Kugeln hintereinander gezogen werden.
, indem sich 3 schwarze und 7 weiße Kugeln befinden und aus dem mit Zurücklegen gezogen wird. Deine Aufgabe ist es dabei, die Wahrscheinlichkeit dafür zu bestimmen, dass aus diesem Gefäß genau 2 schwarze Kugeln hintereinander gezogen werden.
Willst du diese Aufgabe lösen, so musst du dir zunächst überlegen, wie viele Möglichkeiten es gibt, zwei schwarze Kugeln bei insgesamt 8 Zügen aus dem Gefäß zu ziehen. Hast du dies ermittelt, so musst du dir klar machen, mit welcher Wahrscheinlichkeit überhaupt zwei schwarze Kugeln hintereinander aus dem Gefäß entnommen werden.
Die Wahrscheinlichkeit eine schwarze Kugel aus dem Gefäß zu ziehen ermittelst du hier wie oben:
zu ziehen ermittelst du hier wie oben:
 Wird insgesamt 8 Mal aus dem Gefäß eine Kugel mit Zurücklegen gezogen, so gibt es insgesamt 7 Mal die Möglichkeit 2 schwarze Kugeln aus diesem Gefäß zu entnehmen. Die Wahrscheinlichkeit
Wird insgesamt 8 Mal aus dem Gefäß eine Kugel mit Zurücklegen gezogen, so gibt es insgesamt 7 Mal die Möglichkeit 2 schwarze Kugeln aus diesem Gefäß zu entnehmen. Die Wahrscheinlichkeit  im Allgemeinen genau 2 schwarze Kugeln aus dem Gefäß zu ziehen, ergibt sich hier über die Pfadmultiplikation (mit
im Allgemeinen genau 2 schwarze Kugeln aus dem Gefäß zu ziehen, ergibt sich hier über die Pfadmultiplikation (mit  : Wahrscheinlichkeit für weiße Kugel):
: Wahrscheinlichkeit für weiße Kugel):
![\(\begin{array}[t]{rll}
P(A) &=& p_s \cdot p_s \cdot p_w \cdot ... \cdot p_w&\\[5pt]
&=& p_s^2 \cdot p_w^6&\\[5pt]
&=& 0,3^2 \cdot 0,7^6
\end{array}\)](https://mathjax.schullv.de/654a3a2977e96e18f27d5af36217e2cf87b438e6454ffb9bfc8218c7c1aee6a8?color=5a5a5a) Multiplizierst du dieses Ergebnis nun noch mit 7 so hast du die Wahrscheinlichkeit
Multiplizierst du dieses Ergebnis nun noch mit 7 so hast du die Wahrscheinlichkeit  dafür berechnet, genau 2 schwarze Kugeln hintereinander aus dem Gefäß zu ziehen:
dafür berechnet, genau 2 schwarze Kugeln hintereinander aus dem Gefäß zu ziehen:
 .
Die Wahrscheinlichkeit genau zwei schwarze Kugeln hintereinander aus dem Gefäß zu ziehen beträgt also 0,0741 bzw. 7,41%.
.
Die Wahrscheinlichkeit genau zwei schwarze Kugeln hintereinander aus dem Gefäß zu ziehen beträgt also 0,0741 bzw. 7,41%.
Willst du hier diese Wahrscheinlichkeit bestimmen, so betrachtest du zunächst die Zufallsvariable
Wahrscheinlichkeit

Willst du diese Aufgabe lösen, so musst du dir zunächst überlegen, wie viele Möglichkeiten es gibt, zwei schwarze Kugeln bei insgesamt 8 Zügen aus dem Gefäß zu ziehen. Hast du dies ermittelt, so musst du dir klar machen, mit welcher Wahrscheinlichkeit überhaupt zwei schwarze Kugeln hintereinander aus dem Gefäß entnommen werden.
Die Wahrscheinlichkeit eine schwarze Kugel aus dem Gefäß
b)  Berechnen der Wahrscheinlichkeit für eine schwarze Kugel
Der Aufgabenstellung kannst du hier nun entnehmen, dass insgesamt 2 Kugeln aus Gefäß
Berechnen der Wahrscheinlichkeit für eine schwarze Kugel
Der Aufgabenstellung kannst du hier nun entnehmen, dass insgesamt 2 Kugeln aus Gefäß  ohne Zurücklegen gezogen und in das Gefäß
ohne Zurücklegen gezogen und in das Gefäß  gelegt werden. Anschließend wird dann eine Kugel aus Gefäß
gelegt werden. Anschließend wird dann eine Kugel aus Gefäß  gezogen. Deine Aufgabe ist es nun, zu ermitteln, mit welcher Wahrscheinlichkeit diese Kugel schwarz ist.
gezogen. Deine Aufgabe ist es nun, zu ermitteln, mit welcher Wahrscheinlichkeit diese Kugel schwarz ist.
Willst du diese Wahrscheinlichkeit hier berechnen, so musst du hier folgende drei Fälle betrachten: zu ziehen. Die Wahrscheinlichkeit dafür, eine schwarze Kugel aus
zu ziehen. Die Wahrscheinlichkeit dafür, eine schwarze Kugel aus  zu ziehen, wird also maßgeblich von diesen Wahrscheinlichkeiten beeinflusst.
zu ziehen, wird also maßgeblich von diesen Wahrscheinlichkeiten beeinflusst.
Hast du die Wahrscheinlichkeiten für die verschiedenen Fälle ermittelt, so kannst du ausgehend von diesen die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus dem Gefäß ermitteln. Auch hier ergeben sich drei verschiedene Fälle:
ermitteln. Auch hier ergeben sich drei verschiedene Fälle:
Die Wahrscheinlichkeit dafür, dass 2 schwarze Kugeln in Gefäß gelegt werden, ergibt sich hier über die Pfadmultiplikation. Denke dabei daran, dass es sich um ein Ziehen ohne Zurücklegen handelt.
gelegt werden, ergibt sich hier über die Pfadmultiplikation. Denke dabei daran, dass es sich um ein Ziehen ohne Zurücklegen handelt.
![\(\begin{array}[t]{rll}
P(\text{2 schwarze Kugeln}) &=& \frac{6}{10} \cdot \frac{5}{9}& \\[5pt]
&=& \frac{1}{3}
\end{array}\)](https://mathjax.schullv.de/b98469cc47721dd187aaeae3cfcc35e9fceb25757c543afa3db22885275a4ae0?color=5a5a5a) Eine schwarze Kugel:
Eine schwarze Kugel:
Die Wahrscheinlichkeit, dass eine schwarze Kugel in Gefäß gelegt wird, ergibt sich aus der Wahrscheinlichkeit, dass eine schwarze und eine weiße Kugel in Gefäß
gelegt wird, ergibt sich aus der Wahrscheinlichkeit, dass eine schwarze und eine weiße Kugel in Gefäß  gelegt wird. Achte hierbei auf die Reihenfolge.
Keine schwarze Kugel:
gelegt wird. Achte hierbei auf die Reihenfolge.
Keine schwarze Kugel:
Die Wahrscheinlichkeit dafür, dass keine schwarze Kugel ins Gefäß gelegt wird, ergibt sich hier aus der Wahrscheinlichkeit dafür, dass zwei weiße Kugeln ins Gefäß gelegt werden:
gelegt wird, ergibt sich hier aus der Wahrscheinlichkeit dafür, dass zwei weiße Kugeln ins Gefäß gelegt werden:
![\(\begin{array}[t]{rll}
P(\text{keine schwarze Kugeln}) &=& \frac{4}{10} \cdot \frac{3}{9}& \\[5pt]
&=& \frac{2}{15}
\end{array}\)](https://mathjax.schullv.de/9d295068df31f1d58f8a5b31a99b689e92caa6acfae58def5cd700f279888771?color=5a5a5a) 2. Schritt: Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel
Willst du hier nun die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus Gefäß
2. Schritt: Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel
Willst du hier nun die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus Gefäß  berechnen, so musst du auch hier wieder die drei Fälle von oben beachten. Denke dabei daran, dass sich die Anzahl der Kugeln in Gefäß
berechnen, so musst du auch hier wieder die drei Fälle von oben beachten. Denke dabei daran, dass sich die Anzahl der Kugeln in Gefäß  auf 12 erhöht ist und dass die Anzahl der schwarzen Kugel abhängig von dem eingetretenen Fall ist.
Fall 1: Zwei schwarze Kugeln
auf 12 erhöht ist und dass die Anzahl der schwarzen Kugel abhängig von dem eingetretenen Fall ist.
Fall 1: Zwei schwarze Kugeln
Wurden 2 schwarze Kugeln ins Gefäß gelegt, so befinden sich nun insgesamt 5 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit, dass dieser Fall eintritt und dass dann eine schwarze Kugel gezogen wird, ergibt sich wie folgt über die Pfadmultiplikation: Fall 2: Eine schwarze Kugel
Fall 2: Eine schwarze Kugel
Wurde 1 schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 4 schwarze Kugeln in diesem Gefäß. Fall 3: Keine schwarze Kugel
Fall 3: Keine schwarze Kugel
Wurde keine schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 3 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit nun eine schwarze Kugel aus dem Gefäß
Die Wahrscheinlichkeit nun eine schwarze Kugel aus dem Gefäß  zu ziehen ergibt sich über die Pfadaddition. Bilde also die Summe der berechneten Wahrscheinlichkeiten:
Die Wahrscheinlichkeit, unter den neuen Umständen, eine schwarze Kugel aus Gefäß
zu ziehen ergibt sich über die Pfadaddition. Bilde also die Summe der berechneten Wahrscheinlichkeiten:
Die Wahrscheinlichkeit, unter den neuen Umständen, eine schwarze Kugel aus Gefäß  zu ziehen liegt also bei
zu ziehen liegt also bei  bzw. 35 %.
bzw. 35 %.
Willst du diese Wahrscheinlichkeit hier berechnen, so musst du hier folgende drei Fälle betrachten:
- Es werden 2 schwarze Kugeln in
gelegt;
- es wird eine schwarze Kugel in
gelegt und
- es wird keine schwarze Kugel in
gelegt.
Hast du die Wahrscheinlichkeiten für die verschiedenen Fälle ermittelt, so kannst du ausgehend von diesen die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus dem Gefäß
- Die Anzahl der schwarzen Kugeln hat sich um 2 erhöht;
- die Anzahl der schwarzen Kugeln hat sich um 1 erhöht und
- die Anzahl der schwarzen Kugeln hat sich nicht erhöht.
1. Schritt: Wahrscheinlichkeiten, für die drei Fälle
Zwei schwarze Kugeln:
Die Wahrscheinlichkeit dafür, dass 2 schwarze Kugeln in Gefäß
Die Wahrscheinlichkeit, dass eine schwarze Kugel in Gefäß
Die Wahrscheinlichkeit dafür, dass keine schwarze Kugel ins Gefäß
Wurden 2 schwarze Kugeln ins Gefäß gelegt, so befinden sich nun insgesamt 5 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit, dass dieser Fall eintritt und dass dann eine schwarze Kugel gezogen wird, ergibt sich wie folgt über die Pfadmultiplikation:
Wurde 1 schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 4 schwarze Kugeln in diesem Gefäß.
Wurde keine schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 3 schwarze Kugeln in diesem Gefäß.
Aufgabe B1.1
a)  Bestimmen einer Koordinatengleichung für Ebene
Der Aufgabenstellung kannst du entnehmen, dass das Quadrat
Bestimmen einer Koordinatengleichung für Ebene
Der Aufgabenstellung kannst du entnehmen, dass das Quadrat  die Grundfläche einer Pyramide mit der Spitze
die Grundfläche einer Pyramide mit der Spitze  ist. Weiterhin weißt du, dass die Seitenfläche
ist. Weiterhin weißt du, dass die Seitenfläche  in der Ebene
in der Ebene  liegt. Deine Aufgabe ist es dabei, eine Koordinatengleichung der Ebene
liegt. Deine Aufgabe ist es dabei, eine Koordinatengleichung der Ebene  zu bestimmen. Die Koordinatengleichung einer Ebene baut sich dabei wie folgt auf:
zu bestimmen. Die Koordinatengleichung einer Ebene baut sich dabei wie folgt auf:
 mit:
mit:
 bestimmen, so bestimmst du zunächst den Normalenvektor
bestimmen, so bestimmst du zunächst den Normalenvektor  über das Vektorprodukt bzw. Kreuzprodukt. Verwende dazu die Information, dass die Seitenfläche
über das Vektorprodukt bzw. Kreuzprodukt. Verwende dazu die Information, dass die Seitenfläche  der Pyramide in der Ebene
der Pyramide in der Ebene  liegt.
liegt.





 .
.
 Bestimmen des Winkels zwischen den Flächen
Bestimmen des Winkels zwischen den Flächen  und
und  Nun ist es deine Aufgabe, den Winkel
Nun ist es deine Aufgabe, den Winkel  zwischen Seitenfläche
zwischen Seitenfläche  und Grundfläche
und Grundfläche  der Pyramide zu berechnen. Hier gilt es also einen Winkel zwischen zwei Ebenen zu berechnen. Einen Winkel zwischen zwei gegebenen Ebenen berechnest du dabei über folgende Formel:
der Pyramide zu berechnen. Hier gilt es also einen Winkel zwischen zwei Ebenen zu berechnen. Einen Winkel zwischen zwei gegebenen Ebenen berechnest du dabei über folgende Formel:
 mit:
mit:
 der Ebene, in welcher die Grundfläche
der Ebene, in welcher die Grundfläche  liegt, könntest du wie oben über das Kreuzprodukt bestimmen. Vergleichst du jedoch die Variablen der Punkte
liegt, könntest du wie oben über das Kreuzprodukt bestimmen. Vergleichst du jedoch die Variablen der Punkte  ,
,  ,
,  und
und  , mit
, mit
 -Ebene liegen (
-Ebene liegen ( -Koordinate ist überall Null). Ein Vektor, welcher senkrecht auf der Ebene steht, in welcher sich auch die Grundfläche
-Koordinate ist überall Null). Ein Vektor, welcher senkrecht auf der Ebene steht, in welcher sich auch die Grundfläche  befindet, zeigt also in Richtung der
befindet, zeigt also in Richtung der  -Achse. Für den Normalenvektor
-Achse. Für den Normalenvektor  gilt hier also:
gilt hier also:

 Berechnen des Flächeninhalts des Dreiecks
Berechnen des Flächeninhalts des Dreiecks  Zuletzt sollst den Flächeninhalt
Zuletzt sollst den Flächeninhalt  des Dreiecks
des Dreiecks  berechnen. Der Flächeninhalt eines Dreiecks berechnet sich dabei über folgenden Zusammenhang:
berechnen. Der Flächeninhalt eines Dreiecks berechnet sich dabei über folgenden Zusammenhang:
 mit:
mit:






und
: Einträge des Normalenvektors
der Ebene
: Über Punktprobe zu bestimmende Konstante
Hast du den Normalenvektor  der Ebene
der Ebene  bestimmt, so bestimmst du über eine Punktprobe die Konstante
bestimmt, so bestimmst du über eine Punktprobe die Konstante  . Verwende dazu die Koordinaten von Punkt
. Verwende dazu die Koordinaten von Punkt  ,
,  oder
oder  .
.
1. Schritt: Bestimmen des Normalenvektors  über das Vektorprodukt
über das Vektorprodukt
Willst du den Normalenvektor  bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene
bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene  aufspannen. Da die Seitenfläche
aufspannen. Da die Seitenfläche  in der Ebene
in der Ebene  liegt, kannst du hier die Vektoren
liegt, kannst du hier die Vektoren  und
und  verwenden:
verwenden:
Berechne nun wie folgt das Vektorprodukt bzw. Kreuzprodukt der Vektoren  und
und  , um den Normalenvektor
, um den Normalenvektor  zu bestimmen:
zu bestimmen:
Da beim Normalenvektor  nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor  in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante  bestimmst du hier nun, indem du beispielsweise die Koordinaten von
bestimmst du hier nun, indem du beispielsweise die Koordinaten von  mit
mit  für
für  ,
,  und
und  einsetzt und die Gleichung nach
einsetzt und die Gleichung nach  löst:
löst:
Eine Koordinatengleichung der Ebene  lautet also:
lautet also:
: Winkel zwischen den Ebenen
: Normalenvektoren der Ebenen
Willst du also den Winkel  zwischen der Seitenfläche
zwischen der Seitenfläche  und der Grundfläche
und der Grundfläche  berechnen, so benötigst du hier die Normalenvektoren dieser Ebenen. Den Normalenvektor der Ebene
berechnen, so benötigst du hier die Normalenvektoren dieser Ebenen. Den Normalenvektor der Ebene  , in welcher die Seitenfläche
, in welcher die Seitenfläche  liegt, hast du oben schon bestimmt. Der Normalenvektor der Ebene, in welcher die Grundfläche
liegt, hast du oben schon bestimmt. Der Normalenvektor der Ebene, in welcher die Grundfläche  liegt, gilt es noch zu berechnen.
liegt, gilt es noch zu berechnen.
1. Schritt: Bestimmen des gesuchten Normalenvektors
Den Normalenvektor
2. Schritt: Bestimmen des Winkels  Den Winkel
Den Winkel  bestimmst du nun, in dem du
bestimmst du nun, in dem du  und
und  in den oben gezeigten Zusammenhang einsetzt und wie folgt berechnest:
in den oben gezeigten Zusammenhang einsetzt und wie folgt berechnest:
![\(\scriptsize\begin{array}{rll}
\cos(\alpha)&=&\dfrac{\overrightarrow{n_E} \cdot \overrightarrow{n_{ABCD}}}{|\overrightarrow{n_E}| \cdot |\overrightarrow{n_{ABCD}}|} \\
&=&\dfrac{\begin{pmatrix}0 \\ 12 \\ 5\end{pmatrix} \cdot
\begin{pmatrix}0\\0\\1\end{pmatrix}}{\left|\begin{pmatrix}0 \\ 12 \\ 5\end{pmatrix}\right|
\cdot \left|\begin{pmatrix}0 \\ 0 \\ 1\end{pmatrix}\right|}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8b223f4ba85c505f637ecf1d3ff0b17ddb0137aa85418053ee2d2b5b1d07ac95?color=5a5a5a)
![\(\scriptsize\begin{array}{rll}
\cos(\alpha)
&=&\dfrac{0 \cdot 0 + 12 \cdot 0 + 5 \cdot 1}{\sqrt{0^2 + 12^2 + 5^2} \cdot \sqrt{0^2 + 0^2 + 1^2}}\; \\
&=&\;\dfrac{5}{\sqrt{169} \cdot \sqrt{1}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7b0ba4662660b5d75537f177c19e12a41351ebf4479c600343ce10e7fdd527bb?color=5a5a5a)
![\(\scriptsize\begin{array}{rll}
\cos{\alpha}&=&\dfrac{5}{13}&\scriptsize \mid\;\cos^{-1}\\[5pt]
\alpha&=&\cos^{-1}(\frac{5}{13})\;=\;67,38\,\text{°}
\end{array}\)](https://mathjax.schullv.de/c85409122f570133279d1fc377b45ef49963efd7af59ffa10ddacc89531640b4?color=5a5a5a)
Der Winkel zwischen der Seitenfläche  und der Grundfläche
und der Grundfläche  beträgt also 67,38°.
beträgt also 67,38°.
: Grundseite
: Höhe des Dreiecks
Fertige dir eine Skizze des Dreiecks  an, um dir das Lösen dieser Aufgabe einfacher zu gestalten:
an, um dir das Lösen dieser Aufgabe einfacher zu gestalten:

Willst du hier den Flächeninhalt  des Dreiecks
des Dreiecks  bestimmen, so musst du die Länge der Höhe
bestimmen, so musst du die Länge der Höhe  berechnen. Diese Länge ermittelst du, in dem du zunächst die Länge der Strecke
berechnen. Diese Länge ermittelst du, in dem du zunächst die Länge der Strecke  berechnest. Zeichnest du die Seitenansicht der Pyramide
berechnest. Zeichnest du die Seitenansicht der Pyramide  , so kannst du erkennen, dass die Strecke
, so kannst du erkennen, dass die Strecke  eine der Seitenlängen der Pyramiden entspricht:
eine der Seitenlängen der Pyramiden entspricht:

Betrachtest du die Skizze oben näher, so kannst du weiterhin erkennen, dass die Strecke  mit der Höhe
mit der Höhe  der Pyramide und der Hälfte der Grundseitenlänge
der Pyramide und der Hälfte der Grundseitenlänge  in einem rechtwinkligen Dreieck liegt. Diese lässt sich also über den Satz des Pythagoras in diesem Dreieck bestimmen.
in einem rechtwinkligen Dreieck liegt. Diese lässt sich also über den Satz des Pythagoras in diesem Dreieck bestimmen.
Gehe beim Berechnen des Flächeninhalts  also so vor:
also so vor:
- Bestimme die Höhe
der Pyramide
- Bestimme die Grundseitenlänge
- Berechne die Länge der Strecke
- Berechne den Flächeninhalt
1. Schritt: Bestimmen von  und
und  Die Höhe der Pyramide
Die Höhe der Pyramide  ergibt sich aus der
ergibt sich aus der  -Koordinaten der Spitze
-Koordinaten der Spitze  der Pyramide:
der Pyramide:
Die Grundseiten Länge entspricht beispielsweise der Länge des Vektors  , da dieser Vektor eine der Quadratseiten des Quadrates
, da dieser Vektor eine der Quadratseiten des Quadrates  beschreibt:
beschreibt:
2. Schritt: Bestimmen der Länge der Strecke  Betrachtest du die Skizze oben näher, so kannst du erkennen, dass
Betrachtest du die Skizze oben näher, so kannst du erkennen, dass  und
und  die Katheten des betrachteten rechtwinkligen Dreiecks sind. Willst du die Länge der Strecke
die Katheten des betrachteten rechtwinkligen Dreiecks sind. Willst du die Länge der Strecke  über den Satz des Pythagroas bestimmen, so gehst du hier also so vor:
über den Satz des Pythagroas bestimmen, so gehst du hier also so vor:
Setzt du nun  sowie
sowie  in die oben gezeigte Formel für den Flächeninhalt des Dreicks
in die oben gezeigte Formel für den Flächeninhalt des Dreicks  ein, so ergibt sich dieser wie folgt:
ein, so ergibt sich dieser wie folgt:
Der Flächeninhalt des Dreiecks  ist 65\,\text{FE}.
ist 65\,\text{FE}.
b)  Berechnen des Quadervolumens
Der Aufgabenstellung kannst du nun entnehmen, dass nun Quader betrachtet werden, die jeweils vier Eckpunkte auf den Pyramidenkanten und vier Eckpunkte in der Grundfläche der Pyramide haben. Einer dieser Quader hat nun den Eckpunkt
Berechnen des Quadervolumens
Der Aufgabenstellung kannst du nun entnehmen, dass nun Quader betrachtet werden, die jeweils vier Eckpunkte auf den Pyramidenkanten und vier Eckpunkte in der Grundfläche der Pyramide haben. Einer dieser Quader hat nun den Eckpunkt  .
.
Deine Aufgabe ist es nun, das Volumen dieses Quaders zu berechnen. Das Volumen eines Quaders ergibt sich dabei über folgende Formel:
eines Quaders ergibt sich dabei über folgende Formel:
 mit:
mit:

 berechnest du hier, indem du zunächst die Gerade
berechnest du hier, indem du zunächst die Gerade  definierst, auf welcher die Strecke
definierst, auf welcher die Strecke  liegt. Verwende dazu den Ortsvektor
liegt. Verwende dazu den Ortsvektor  von Punkt
von Punkt  als Stütz- und den Vektor
als Stütz- und den Vektor  als Richtungsvektor:
als Richtungsvektor:

![\(\begin{array}{rll}
\overrightarrow{OR}&=& \overrightarrow{x_g}\\[5pt]
\begin{pmatrix}2,5\\2,5\\z\end{pmatrix}&=& \begin{pmatrix}5 \\ 5 \\ 0\end{pmatrix} + t \cdot \begin{pmatrix}-5 \\ -5 \\ 12\end{pmatrix}\\
\end{array}\)](https://mathjax.schullv.de/353a6f18a1e7c00d6022885ce914baa02c921b0a5e36f376783f508a47ab7b15?color=5a5a5a)

 Berechnen der Koordinaten des Eckpunktes
Nun soll ein weiterer Quader betrachtet werden, bei dem es sich um einen Würfel handelt. Dabei sollte dir bekannt sein, dass bei einem Würfel Länge, Breite und Höhe übereinstimmen. Deine Aufgabe ist es nun die Koordinaten von dessen Eckpunkt auf der Kante
Berechnen der Koordinaten des Eckpunktes
Nun soll ein weiterer Quader betrachtet werden, bei dem es sich um einen Würfel handelt. Dabei sollte dir bekannt sein, dass bei einem Würfel Länge, Breite und Höhe übereinstimmen. Deine Aufgabe ist es nun die Koordinaten von dessen Eckpunkt auf der Kante  zu bestimmen.
zu bestimmen.
Wie oben schon beschrieben, bestimmte der Punkt unter anderem Breite und Länge des Würfels. Dabei entsprach gerade das Doppelte der
unter anderem Breite und Länge des Würfels. Dabei entsprach gerade das Doppelte der  -Koordinate der Länge und das Doppelte der
-Koordinate der Länge und das Doppelte der  -Koordinate der Breite des Würfels.
-Koordinate der Breite des Würfels.
Da der hier zu bestimmende Punkt auf der Kante
auf der Kante  liegt, werden dessen Koordinaten von Gerade
liegt, werden dessen Koordinaten von Gerade  bestimmt. Von oben weißt du, dass dessen
bestimmt. Von oben weißt du, dass dessen  - und
- und  -Koordinate mit denen von Punkt
-Koordinate mit denen von Punkt  , der unterhalb von
, der unterhalb von  liegt, übereinstimmt.
liegt, übereinstimmt.
Daraus folgt, dass die -Koordinate dem Doppelten der
-Koordinate dem Doppelten der  - und
- und  -Koordinaten von
-Koordinaten von  entsprechen muss, damit es sich beim betrachteten Quader um einen Würfel handelt.
entsprechen muss, damit es sich beim betrachteten Quader um einen Würfel handelt.
![\(\begin{array}[t]{rll}
\overrightarrow{OR_t} &=& \begin{pmatrix}5 \\ 5 \\ 0\end{pmatrix} + t \cdot \begin{pmatrix}-5 \\ -5 \\ 12\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}5 - 5 \cdot t \\ 5 - 5 \cdot t \\ 12 \cdot t\end{pmatrix}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b4407aee8759f8a20438936b6e3fc5944775dde4caa2cc15ac4ce24f36b73734?color=5a5a5a)

![\(\begin{array}[t]{rll}
2 \cdot x_1&=& x_3& \\[5pt]
2 \cdot (5 - 5 \cdot t)&=& 12 \cdot t& \\[5pt]
10 - 10 \cdot t&=& 12 \cdot t&\quad \scriptsize \mid\;+10 \cdot t \\[5pt]
10&=& 22t&\quad \scriptsize \mid\; :22 \\[5pt]
\frac{5}{11}&=& t&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/be7851180f8927b74f56b2aa5d03ddd0db63b61f9b98992a78d22fb0d92abf8d?color=5a5a5a)
Deine Aufgabe ist es nun, das Volumen dieses Quaders zu berechnen. Das Volumen
: Länge des Quaders
: Breite des Quaders
: Höhe des Quaders
Bevor du also das Volumen des Quaders bestimmen kannst, musst du dessen Länge, Breite und Höhe bestimmen. Fertige dir dazu eine Skizze des Sachverhalts an, in welche du zunächst die Pyramide  und den Punkt
und den Punkt  einzeichnest:
einzeichnest:

Vergleichst du die Koordinaten von  und dem Punkt
und dem Punkt  , so kannst du erkennen, dass der Punkt
, so kannst du erkennen, dass der Punkt  auf dem Ortsvektor
auf dem Ortsvektor  liegt. Folglich liegt der darüberliegende Punkt
liegt. Folglich liegt der darüberliegende Punkt  des Quaders auf der Strecke
des Quaders auf der Strecke  . Willst du also die Höhe des Quaders berechnen, so bestimmst du die Länge des Vektors
. Willst du also die Höhe des Quaders berechnen, so bestimmst du die Länge des Vektors  . Berechne dazu die Koordinaten von
. Berechne dazu die Koordinaten von  über die Gerade, auf welcher die Strecke
über die Gerade, auf welcher die Strecke  liegt.
liegt.
Die Länge und die Breite des Quaders ermittelst du, indem du die relative Lage des Punktes zu den Koordinatenachsen näher betrachtest.
zu den Koordinatenachsen näher betrachtest.
Die Länge und die Breite des Quaders ermittelst du, indem du die relative Lage des Punktes
1. Schritt: Berechnen der Quaderhöhe
Die Quaderhöhe
Da der Punkt  senkrecht oberhalb des Punkte
senkrecht oberhalb des Punkte  liegt, weißt du, dass für dessen Koordinaten folgendes gelten muss:
liegt, weißt du, dass für dessen Koordinaten folgendes gelten muss:  .
.
Setzt du nun den Ortsvektor  von
von  mit der Geradengleichung von
mit der Geradengleichung von  gleich, so kannst du wie folgt die vollständigen Koordinaten von
gleich, so kannst du wie folgt die vollständigen Koordinaten von  bestimmen:
bestimmen:
Übertrage diese Gleichung wie folgt in ein Gleichungssystem, um die vollständigen Koordinaten von  zu bestimmen:
zu bestimmen:
Die vollständigen Koordinaten von Punkt  sind also:
sind also:  . Vergleichst du nun die Koordinaten von
. Vergleichst du nun die Koordinaten von  und
und  , so kannst du erkennen, dass die Höhe des Quaders offensichtlich
, so kannst du erkennen, dass die Höhe des Quaders offensichtlich  sein muss.
sein muss.
2. Schritt: Berechnen der Länge und der Breite des Quaders
Willst du die Länge und die Breite des Quaders bestimmen, so betrachtest du die Koordinaten von  .
.  hat eine
hat eine  -Koordinate von
-Koordinate von  . Das heißt der Abstand von
. Das heißt der Abstand von  zur
zur  -Achse beträgt 2,5. Da es sich um einen Quader handelt, dessen Grundfläche in der Fläche
-Achse beträgt 2,5. Da es sich um einen Quader handelt, dessen Grundfläche in der Fläche  liegt, muss für dessen Länge gelten:
liegt, muss für dessen Länge gelten:
.
.

3. Schritt: Berechnen des Quadervolumens  Das Quadervolumen
Das Quadervolumen  ergibt sich nun über den obigen Ansatz wie folgt:
ergibt sich nun über den obigen Ansatz wie folgt:
 .
Der Quader besitzt ein Volumen von 150 VE.
.
Der Quader besitzt ein Volumen von 150 VE.
Wie oben schon beschrieben, bestimmte der Punkt
Da der hier zu bestimmende Punkt
Daraus folgt, dass die
1. Schritt: Bestimmen der allgemeinen Koordinaten von  Die allgemeinen Koordinaten von
Die allgemeinen Koordinaten von  ergeben sich wie folgt aus der Gleichung von Gerade
ergeben sich wie folgt aus der Gleichung von Gerade  :
:
2. Schritt: Bestimmen der gesuchten Koordinaten von  Wie oben erwähnt, handelt es sich dann um einen Würfel, wenn die
Wie oben erwähnt, handelt es sich dann um einen Würfel, wenn die  -Koordinate von
-Koordinate von  dem Doppelten der
dem Doppelten der  - und der
- und der  -Koordinaten dieses Punktes entspricht. Berechne mit
-Koordinaten dieses Punktes entspricht. Berechne mit  die gesuchten Koordinaten von
die gesuchten Koordinaten von  über folgende Gleichung:
über folgende Gleichung:
Für  muss also
muss also  gelten. Für die gesuchten Koordinaten gilt also:
gelten. Für die gesuchten Koordinaten gilt also:
Die gesuchten Koordinaten des Eckpunktes auf der Kante  sind also
sind also  .
.
Aufgabe 1.2
a)  Wahrscheinlichkeit, dass mind. 12 Mal eine schwarze Kugel gezogen wird
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 20 Mal eine Kugel aus dem Gefäß
Wahrscheinlichkeit, dass mind. 12 Mal eine schwarze Kugel gezogen wird
Der Aufgabenstellung kannst du entnehmen, dass insgesamt 20 Mal eine Kugel aus dem Gefäß  gezogen wird. Die Kugeln werden dabei jeweils wieder ins Gefäß zurückgelegt, weswegen es sich hier um ein Ziehen mit Zurücklegen handelt. Im Gefäß
gezogen wird. Die Kugeln werden dabei jeweils wieder ins Gefäß zurückgelegt, weswegen es sich hier um ein Ziehen mit Zurücklegen handelt. Im Gefäß  befinden sich 6 schwarze und 4 weiße Kugel. Deine Aufgabe ist es nun, die Wahrscheinlichkeit dafür zu bestimmen, dass bei 20 Zügen mindestens 12 Mal eine schwarze Kugeln gezogen wird.
befinden sich 6 schwarze und 4 weiße Kugel. Deine Aufgabe ist es nun, die Wahrscheinlichkeit dafür zu bestimmen, dass bei 20 Zügen mindestens 12 Mal eine schwarze Kugeln gezogen wird.
Willst du hier diese Wahrscheinlichkeit bestimmen, so betrachtest du zunächst die Zufallsvariable . Zufallsvariable
. Zufallsvariable  beschreibt dabei die Anzahl der gezogenen schwarzen Kugeln. Da bei diesem Zufallsversuch nur die Anzahl der gezogenen schwarzen Kugeln relevant ist und es sich um ein Ziehen mit Zurücklegen handelt, ist Zufallsvariable
beschreibt dabei die Anzahl der gezogenen schwarzen Kugeln. Da bei diesem Zufallsversuch nur die Anzahl der gezogenen schwarzen Kugeln relevant ist und es sich um ein Ziehen mit Zurücklegen handelt, ist Zufallsvariable  binomialverteilt. Da insgesamt
binomialverteilt. Da insgesamt  Mal gezogen wird ist
Mal gezogen wird ist  .
.
Wahrscheinlichkeit ergibt sich aus der Gesamtanzahl der schwarzen Kugeln unter allen Kugeln. Da hier die Wahrscheinlichkeit dafür gesucht wird, dass mindestens 12 Mal eine schwarze Kugeln gezogen wird, muss für die Zufallsvariable
ergibt sich aus der Gesamtanzahl der schwarzen Kugeln unter allen Kugeln. Da hier die Wahrscheinlichkeit dafür gesucht wird, dass mindestens 12 Mal eine schwarze Kugeln gezogen wird, muss für die Zufallsvariable  hier folgendes gelten:
hier folgendes gelten:
 .
Diese Wahrscheinlichkeit kannst du mit deinem GTR berechnen. Dazu musst du den binomCdf-Befehl verwenden. Da dieser aber nur Ausdrücke wie
.
Diese Wahrscheinlichkeit kannst du mit deinem GTR berechnen. Dazu musst du den binomCdf-Befehl verwenden. Da dieser aber nur Ausdrücke wie  berechnen kann, musst du hier zunächst wie folgt das Gegenereignis zu
berechnen kann, musst du hier zunächst wie folgt das Gegenereignis zu  bilden:
bilden:
![\(\begin{array}[t]{rll}
P(X \geq 12)&=& 1 - P(X \lt 12)& \\[5pt]
&=& 1 - P(X \leq 11)
\end{array}\)](https://mathjax.schullv.de/05b8b0c35cb1ee195f383bef73bdc2920be41b7ba320c99c96c5688a8998b78f?color=5a5a5a) Insgesamt befinden sich 10 Kugel im Gefäß, weswegen die Wahrscheinlichkeit
Insgesamt befinden sich 10 Kugel im Gefäß, weswegen die Wahrscheinlichkeit  eine schwarze Kugel zu ziehen, die folgende ist:
eine schwarze Kugel zu ziehen, die folgende ist:
 Nun weißt du, dass
Nun weißt du, dass  ,
,  gilt. Wende den binomCdf-Befehl wie in den Schaubildern unten an, um hier die gesuchte Wahrscheinlichkeit zu berechnen. Greife dazu aber zunächst über menu
gilt. Wende den binomCdf-Befehl wie in den Schaubildern unten an, um hier die gesuchte Wahrscheinlichkeit zu berechnen. Greife dazu aber zunächst über menu  Stat
Stat  DIST
DIST  BINM auf diesen zu.
BINM auf diesen zu.
 Die Wahrscheinlichkeit, mindestens 12 schwarze Kugeln aus Gefäß
Die Wahrscheinlichkeit, mindestens 12 schwarze Kugeln aus Gefäß  zu ziehen beträgt also etwa 59,6 %.
zu ziehen beträgt also etwa 59,6 %.
 Wahrscheinlichkeit, dass 2 schwarze Kugeln hintereinander gezogen werden
Nun betrachtest du Gefäß
Wahrscheinlichkeit, dass 2 schwarze Kugeln hintereinander gezogen werden
Nun betrachtest du Gefäß  , indem sich 3 schwarze und 7 weiße Kugeln befinden und aus dem mit Zurücklegen gezogen wird. Deine Aufgabe ist es dabei, die Wahrscheinlichkeit dafür zu bestimmen, dass aus diesem Gefäß genau 2 schwarze Kugeln hintereinander gezogen werden.
, indem sich 3 schwarze und 7 weiße Kugeln befinden und aus dem mit Zurücklegen gezogen wird. Deine Aufgabe ist es dabei, die Wahrscheinlichkeit dafür zu bestimmen, dass aus diesem Gefäß genau 2 schwarze Kugeln hintereinander gezogen werden.
Willst du diese Aufgabe lösen, so musst du dir zunächst überlegen, wie viele Möglichkeiten es gibt, zwei schwarze Kugeln bei insgesamt 8 Zügen aus dem Gefäß zu ziehen. Hast du dies ermittelt, so musst du dir klar machen, mit welcher Wahrscheinlichkeit überhaupt zwei schwarze Kugeln hintereinander aus dem Gefäß entnommen werden.
Die Wahrscheinlichkeit eine schwarze Kugel aus dem Gefäß zu ziehen ermittelst du hier wie oben:
zu ziehen ermittelst du hier wie oben:
 Wird insgesamt 8 Mal aus dem Gefäß eine Kugel mit Zurücklegen gezogen, so gibt es insgesamt 7 Mal die Möglichkeit 2 schwarze Kugeln aus diesem Gefäß zu entnehmen. Die Wahrscheinlichkeit
Wird insgesamt 8 Mal aus dem Gefäß eine Kugel mit Zurücklegen gezogen, so gibt es insgesamt 7 Mal die Möglichkeit 2 schwarze Kugeln aus diesem Gefäß zu entnehmen. Die Wahrscheinlichkeit  im Allgemeinen genau 2 schwarze Kugeln aus dem Gefäß zu ziehen, ergibt sich hier über die Pfadmultiplikation (mit
im Allgemeinen genau 2 schwarze Kugeln aus dem Gefäß zu ziehen, ergibt sich hier über die Pfadmultiplikation (mit  : Wahrscheinlichkeit für weiße Kugel):
: Wahrscheinlichkeit für weiße Kugel):
![\(\begin{array}[t]{rll}
P(A)&=& p_s \cdot p_s \cdot p_w \cdot ... \cdot p_w& \\[5pt]
&=& p_s^2 \cdot p_w^6& \\[5pt]
&=& 0,3^2 \cdot 0,7^6
\end{array}\)](https://mathjax.schullv.de/8e2f55b153e3c42d1eb164f65b9c5b8dee17f920bc62c7e90bcebb21b0adb9e2?color=5a5a5a) Multiplizierst du dieses Ergebnis nun noch mit 7 so hast du die Wahrscheinlichkeit
Multiplizierst du dieses Ergebnis nun noch mit 7 so hast du die Wahrscheinlichkeit  dafür berechnet, genau 2 schwarze Kugeln hintereinander aus dem Gefäß zu ziehen:
dafür berechnet, genau 2 schwarze Kugeln hintereinander aus dem Gefäß zu ziehen:
 Die Wahrscheinlichkeit genau zwei schwarze Kugeln hintereinander aus dem Gefäß zu ziehen beträgt also 0,0741 bzw. 7,41%.
Die Wahrscheinlichkeit genau zwei schwarze Kugeln hintereinander aus dem Gefäß zu ziehen beträgt also 0,0741 bzw. 7,41%.
Willst du hier diese Wahrscheinlichkeit bestimmen, so betrachtest du zunächst die Zufallsvariable
Wahrscheinlichkeit

Willst du diese Aufgabe lösen, so musst du dir zunächst überlegen, wie viele Möglichkeiten es gibt, zwei schwarze Kugeln bei insgesamt 8 Zügen aus dem Gefäß zu ziehen. Hast du dies ermittelt, so musst du dir klar machen, mit welcher Wahrscheinlichkeit überhaupt zwei schwarze Kugeln hintereinander aus dem Gefäß entnommen werden.
Die Wahrscheinlichkeit eine schwarze Kugel aus dem Gefäß
b)  Berechnen der Wahrscheinlichkeit für eine schwarze Kugel
Der Aufgabenstellung kannst du hier nun entnehmen, dass insgesamt 2 Kugeln aus Gefäß
Berechnen der Wahrscheinlichkeit für eine schwarze Kugel
Der Aufgabenstellung kannst du hier nun entnehmen, dass insgesamt 2 Kugeln aus Gefäß  ohne Zurücklegen gezogen und in das Gefäß
ohne Zurücklegen gezogen und in das Gefäß  gelegt werden. Anschließend wird dann eine Kugel aus Gefäß
gelegt werden. Anschließend wird dann eine Kugel aus Gefäß  gezogen. Deine Aufgabe ist es nun, zu ermitteln, mit welcher Wahrscheinlichkeit diese Kugel schwarz ist.
gezogen. Deine Aufgabe ist es nun, zu ermitteln, mit welcher Wahrscheinlichkeit diese Kugel schwarz ist.
Willst du diese Wahrscheinlichkeit hier berechnen, so musst du hier folgende drei Fälle betrachten: zu ziehen. Die Wahrscheinlichkeit dafür, eine schwarze Kugel aus
zu ziehen. Die Wahrscheinlichkeit dafür, eine schwarze Kugel aus  zu ziehen, wird also maßgeblich von diesen Wahrscheinlichkeiten beeinflusst.
zu ziehen, wird also maßgeblich von diesen Wahrscheinlichkeiten beeinflusst.
Hast du die Wahrscheinlichkeiten für die verschiedenen Fälle ermittelt, so kannst du ausgehend von diesen die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus dem Gefäß ermitteln. Auch hier ergeben sich drei verschiedene Fälle:
ermitteln. Auch hier ergeben sich drei verschiedene Fälle:
Die Wahrscheinlichkeit dafür, dass 2 schwarze Kugeln in Gefäß gelegt werden, ergibt sich hier über die Pfadmultiplikation. Denke dabei daran, dass es sich um ein Ziehen ohne Zurücklegen handelt.
gelegt werden, ergibt sich hier über die Pfadmultiplikation. Denke dabei daran, dass es sich um ein Ziehen ohne Zurücklegen handelt.
 Eine schwarze Kugel:
Eine schwarze Kugel:
Die Wahrscheinlichkeit, dass eine schwarze Kugel in Gefäß gelegt wird, ergibt sich aus der Wahrscheinlichkeit, dass eine schwarze und eine weiße Kugel in Gefäß
gelegt wird, ergibt sich aus der Wahrscheinlichkeit, dass eine schwarze und eine weiße Kugel in Gefäß  gelegt wird. Achte hierbei auf die Reihenfolge.
Keine schwarze Kugel:
gelegt wird. Achte hierbei auf die Reihenfolge.
Keine schwarze Kugel:
Die Wahrscheinlichkeit dafür, dass keine schwarze Kugel ins Gefäß gelegt wird, ergibt sich hier aus der Wahrscheinlichkeit dafür, dass zwei weiße Kugeln ins Gefäß gelegt werden:
gelegt wird, ergibt sich hier aus der Wahrscheinlichkeit dafür, dass zwei weiße Kugeln ins Gefäß gelegt werden:
![\(\begin{array}[t]{rll}
P(\text{keine schwarze Kugeln})&=& \frac{4}{10} \cdot \frac{3}{9}& \\[5pt]
&=&\frac{2}{15}
\end{array}\)](https://mathjax.schullv.de/1f9f57f85fb0b88bc7f3b4078b4a02543410f4eb9d0f35c5ed4a444e850e7b26?color=5a5a5a) 2. Schritt: Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel
Willst du hier nun die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus Gefäß
2. Schritt: Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel
Willst du hier nun die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus Gefäß  berechnen, so musst du auch hier wieder die drei Fälle von oben beachten. Denke dabei daran, dass sich die Anzahl der Kugeln in Gefäß
berechnen, so musst du auch hier wieder die drei Fälle von oben beachten. Denke dabei daran, dass sich die Anzahl der Kugeln in Gefäß  auf 12 erhöht ist und dass die Anzahl der schwarzen Kugel abhängig von dem eingetretenen Fall ist.
Fall 1: Zwei schwarze Kugeln
auf 12 erhöht ist und dass die Anzahl der schwarzen Kugel abhängig von dem eingetretenen Fall ist.
Fall 1: Zwei schwarze Kugeln
Wurden 2 schwarze Kugeln ins Gefäß gelegt, so befinden sich nun insgesamt 5 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit, dass dieser Fall eintritt und dass dann eine schwarze Kugel gezogen wird, ergibt sich wie folgt über die Pfadmultiplikation: Fall 2: Eine schwarze Kugel
Fall 2: Eine schwarze Kugel
Wurde 1 schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 4 schwarze Kugeln in diesem Gefäß. Fall 3: Keine schwarze Kugel
Fall 3: Keine schwarze Kugel
Wurde keine schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 3 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit nun eine schwarze Kugel aus dem Gefäß
Die Wahrscheinlichkeit nun eine schwarze Kugel aus dem Gefäß  zu ziehen ergibt sich über die Pfadaddition. Bilde also die Summe der berechneten Wahrscheinlichkeiten:
Die Wahrscheinlichkeit, unter den neuen Umständen, eine schwarze Kugel aus Gefäß
zu ziehen ergibt sich über die Pfadaddition. Bilde also die Summe der berechneten Wahrscheinlichkeiten:
Die Wahrscheinlichkeit, unter den neuen Umständen, eine schwarze Kugel aus Gefäß  zu ziehen liegt also bei
zu ziehen liegt also bei  bzw. 35 %.
bzw. 35 %.
Willst du diese Wahrscheinlichkeit hier berechnen, so musst du hier folgende drei Fälle betrachten:
- Es werden 2 schwarze Kugeln in
gelegt;
- es wird eine schwarze Kugel in
gelegt und
- es wird keine schwarze Kugel in
gelegt.
Hast du die Wahrscheinlichkeiten für die verschiedenen Fälle ermittelt, so kannst du ausgehend von diesen die Wahrscheinlichkeit für das Ziehen einer schwarzen Kugel aus dem Gefäß
- Die Anzahl der schwarzen Kugeln hat sich um 2 erhöht;
- die Anzahl der schwarzen Kugeln hat sich um 1 erhöht und
- die Anzahl der schwarzen Kugeln hat sich nicht erhöht.
1. Schritt: Wahrscheinlichkeiten, für die drei Fälle
Zwei schwarze Kugeln:
Die Wahrscheinlichkeit dafür, dass 2 schwarze Kugeln in Gefäß
Die Wahrscheinlichkeit, dass eine schwarze Kugel in Gefäß
Die Wahrscheinlichkeit dafür, dass keine schwarze Kugel ins Gefäß
Wurden 2 schwarze Kugeln ins Gefäß gelegt, so befinden sich nun insgesamt 5 schwarze Kugeln in diesem Gefäß. Die Wahrscheinlichkeit, dass dieser Fall eintritt und dass dann eine schwarze Kugel gezogen wird, ergibt sich wie folgt über die Pfadmultiplikation:
Wurde 1 schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 4 schwarze Kugeln in diesem Gefäß.
Wurde keine schwarze Kugel ins Gefäß gelegt, so befinden sich nun insgesamt 3 schwarze Kugeln in diesem Gefäß.