Wahlteil B1
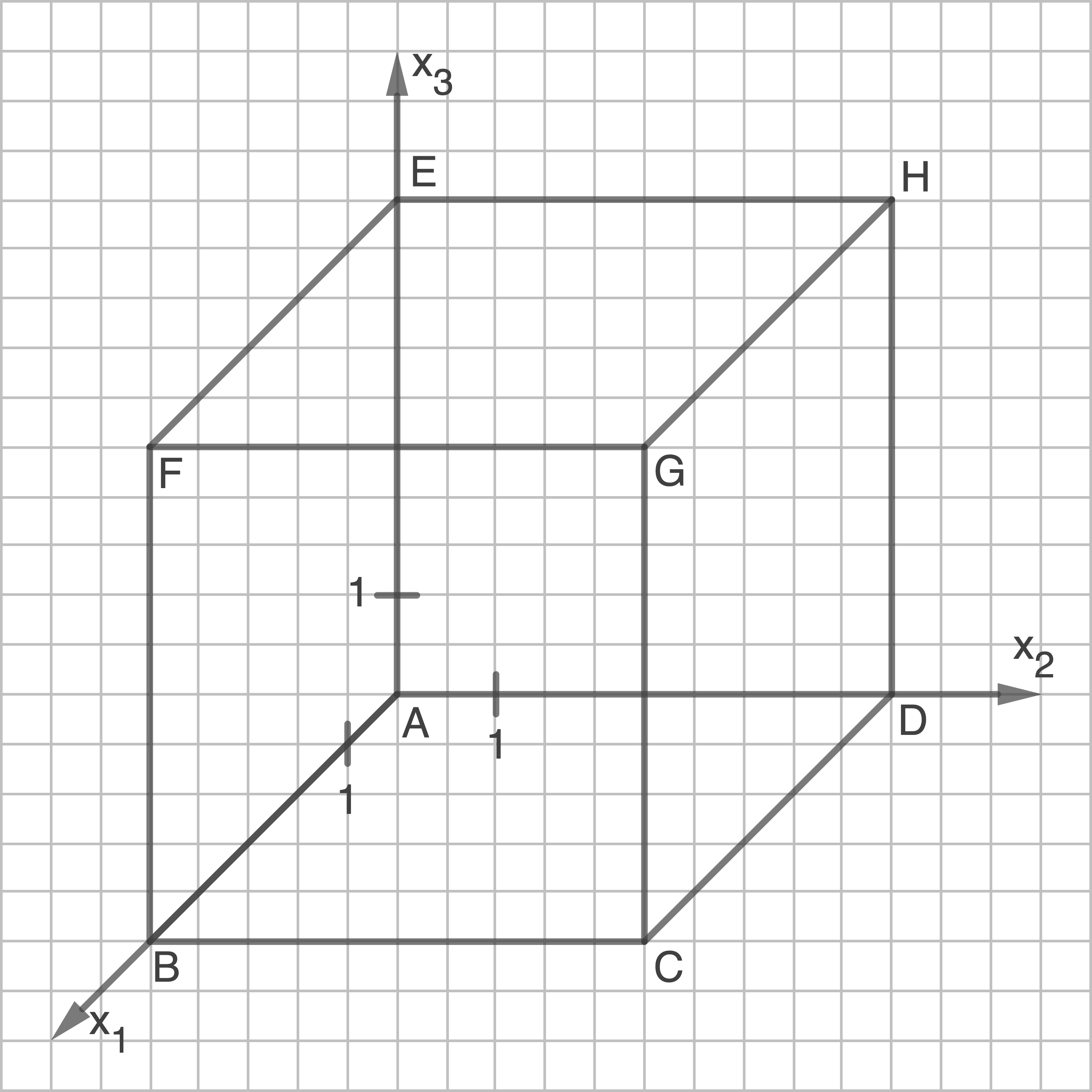
Die Abbildung zeigt den Würfel  mit
mit  und
und  in einem kartesischen Koordinatensystem.
in einem kartesischen Koordinatensystem.
Die Ebene schneidet die Kanten des Würfels unter anderem in den Punkten
schneidet die Kanten des Würfels unter anderem in den Punkten  ,
,  ,
,  und
und  .
.
Die Ebene

a)
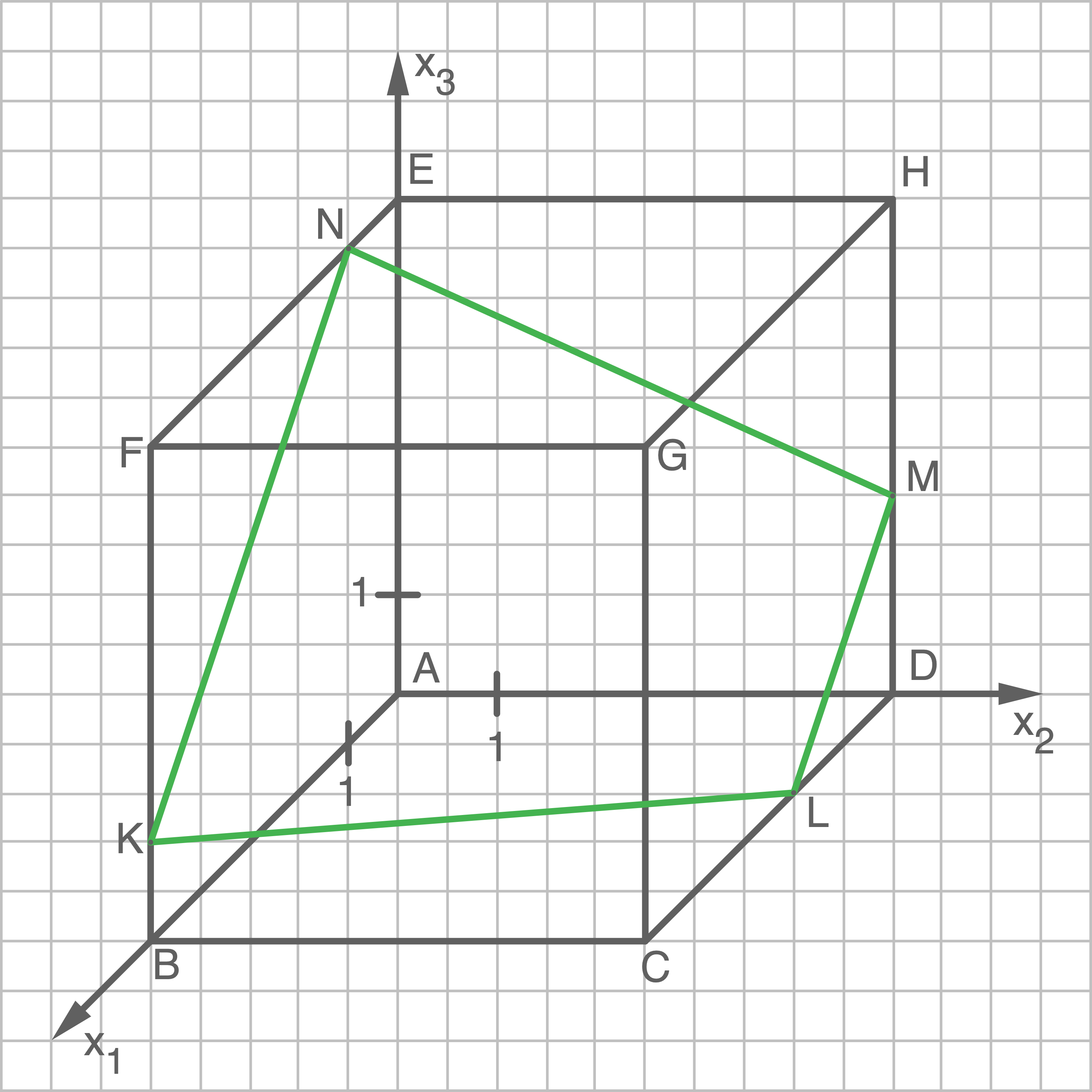
Zeichne das Viereck  in die Abbildung ein.
in die Abbildung ein.
Zeige, dass das Viereck ein Trapez ist und zwei gleich lange Seiten hat.
ein Trapez ist und zwei gleich lange Seiten hat.
Ermittle eine Gleichung der Ebene in Koordinatenform.
in Koordinatenform.
Gib die Koordinaten des Schnittpunkts von mit der
mit der  -Achse an.
-Achse an.
[Teilergebnis: ]
]
Zeige, dass das Viereck
Ermittle eine Gleichung der Ebene
Gib die Koordinaten des Schnittpunkts von
[Teilergebnis:
(5 VP)
b)
Die Spitze einer Pyramide mit der Grundfläche  liegt auf der Strecke
liegt auf der Strecke  . Untersuche, ob die Höhe dieser Pyramide
. Untersuche, ob die Höhe dieser Pyramide  betragen kann.
betragen kann.
(2 VP)
c)
Betrachtet wird die Schar der Geraden
 mit
mit  .
Begründe, dass keine Gerade der Schar in der Ebene mit der Gleichung
.
Begründe, dass keine Gerade der Schar in der Ebene mit der Gleichung  liegt.
liegt.
Gegeben ist die Ebene .
.
Untersuche, ob die Schnittgerade von und
und  zur betrachteten Schar gehört.
zur betrachteten Schar gehört.
Gegeben ist die Ebene
Untersuche, ob die Schnittgerade von
(3 VP)
a)
Viereck einzeichnen
 Trapezform mit zwei gleich langen Seiten zeigen
Der Abbildung kann entnommen werden, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten
Trapezform mit zwei gleich langen Seiten zeigen
Der Abbildung kann entnommen werden, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten ![\([NK]\)](https://mathjax.schullv.de/8480de8fe2873bbe141faf9804141947d1e8b2f8d535f23950840fe154ac1a26?color=5a5a5a) und
und ![\([ML]\)](https://mathjax.schullv.de/c4aadb329afbef34161540f4ed08e5c28d2b43a95caf482737c5d14b230de22b?color=5a5a5a) sind. Für die zugehörigen Verbindungsvektoren folgt:
sind. Für die zugehörigen Verbindungsvektoren folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{NK} &=& \pmatrix{4\\0\\-4} \\[5pt]
\overrightarrow{ML} &=& \pmatrix{2\\0\\-2}
\end{array}\)](https://mathjax.schullv.de/01a2c8c8ff916d888e97be13722025a8c1e65acf15fdbcf06a28ba34c46090f2?color=5a5a5a) Es gilt
Es gilt  Die beiden Vektoren
Die beiden Vektoren  und
und  sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten
sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten ![\([NK]\)](https://mathjax.schullv.de/8480de8fe2873bbe141faf9804141947d1e8b2f8d535f23950840fe154ac1a26?color=5a5a5a) und
und ![\([ML]\)](https://mathjax.schullv.de/c4aadb329afbef34161540f4ed08e5c28d2b43a95caf482737c5d14b230de22b?color=5a5a5a) parallel zueinander. Es handelt sich bei dem Viereck
parallel zueinander. Es handelt sich bei dem Viereck  daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass die beiden anderen gegenüberliegenden Seiten gleich lang sind. Die Länge der Seiten
daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass die beiden anderen gegenüberliegenden Seiten gleich lang sind. Die Länge der Seiten ![\([NM]\)](https://mathjax.schullv.de/56816052ea11e43c3aee13ed07231881a342472957b84562050052e797ca1d06?color=5a5a5a) und
und ![\([KL]\)](https://mathjax.schullv.de/dc04ee28de71778a2cb40846547f15e115488f4b96d8947ad535acc4ab30b675?color=5a5a5a) kannst du mithilfe des Vektorbetrags berechnen.
kannst du mithilfe des Vektorbetrags berechnen.
![\(\begin{array}[t]{rll}
\overline{NM}&=& \left|\overrightarrow{NM} \right| \\[5pt]
&=& \left|\pmatrix{-1\\5\\-3} \right| \\[5pt]
&=& \sqrt{(-1)^2 + 5^2 + (-3)^2} \\[5pt]
&=& \sqrt{35} \\[10pt]
\overline{KL}&=& \left|\overrightarrow{KL} \right| \\[5pt]
&=& \left|\pmatrix{-3\\5\\-1} \right| \\[5pt]
&=& \sqrt{(-3)^2 + 5^2 + (-1)^2} \\[5pt]
&=& \sqrt{35} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/c4f9c3699714c94ac2afca953acc0f6adb875be96f9bb7a5d9fb67144be1c094?color=5a5a5a) Es ist also
Es ist also  Die beiden gegenüberliegenden Seiten
Die beiden gegenüberliegenden Seiten ![\([NM]\)](https://mathjax.schullv.de/56816052ea11e43c3aee13ed07231881a342472957b84562050052e797ca1d06?color=5a5a5a) und
und ![\([KL]\)](https://mathjax.schullv.de/dc04ee28de71778a2cb40846547f15e115488f4b96d8947ad535acc4ab30b675?color=5a5a5a) sind also gleich lang. Das Viereck
sind also gleich lang. Das Viereck  ist also ein Trapez, bei dem zwei gegenüberliegende Seiten gleich lang sind.
Ebenengleichung in Koordinatenform ermitteln
Ein Normalenvektor von
ist also ein Trapez, bei dem zwei gegenüberliegende Seiten gleich lang sind.
Ebenengleichung in Koordinatenform ermitteln
Ein Normalenvektor von  kann über das Kreuzprodukt zweier Verbindungsvektoren beispielsweise der drei Punkte
kann über das Kreuzprodukt zweier Verbindungsvektoren beispielsweise der drei Punkte 
 und
und  bestimmt werden:
bestimmt werden:
![\(\begin{array}[t]{rll}
\overrightarrow{n} &=& \overrightarrow{KL}\times \overrightarrow{KM} \\[5pt]
&=& \pmatrix{-3\\5\\-1}\times \pmatrix{-5\\5\\1} \\[5pt]
&=& \pmatrix{ 5\cdot 1 - (-1)\cdot 5 \\ (-1)\cdot (-5) - (-3) \cdot 1 \\ (-3)\cdot 5 - 5\cdot (-5) } \\[5pt]
&=& \pmatrix{10 \\ 8 \\ 10 } \\[5pt]
&=& 2\cdot \pmatrix{5\\4\\5} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ebae4e9973e0ac65e487ccafa26060a3fa677cf297c6592b4214d58caf5457f4?color=5a5a5a) Für die Ebenengleichung kann nun sowohl der gekürzte Normalenvektor als auch der ursprüngliche verwendet werden. Mit einer Punktprobe mithilfe der Koordinaten eines der vier Punkte (z.B.
Für die Ebenengleichung kann nun sowohl der gekürzte Normalenvektor als auch der ursprüngliche verwendet werden. Mit einer Punktprobe mithilfe der Koordinaten eines der vier Punkte (z.B.  ) folgt:
) folgt:
![\(\begin{array}[t]{rll}
5\cdot x_1 +4\cdot x_2 +5\cdot x_3 &=& d \\[5pt]
5\cdot 1 +4\cdot 0 +5 \cdot 5 &=& d \\[5pt]
30&=& d
\end{array}\)](https://mathjax.schullv.de/d64e5f34c663b468392cfd7d671169421a364cbd834720bff0e334e3bed33bd9?color=5a5a5a) Eine Gleichung von
Eine Gleichung von  in Koordinatenform lautet:
in Koordinatenform lautet:
 Koordinaten des Schnittpunkts angeben
Für die Punkte auf der
Koordinaten des Schnittpunkts angeben
Für die Punkte auf der  -Achse gilt
-Achse gilt 
![\(\begin{array}[t]{rll}
5x_1+4x_2+5x_3 &=& 30 \\[5pt]
5x_1 +4\cdot 0 +5\cdot 0 &=& 30 \\[5pt]
5x_1 &=& 30 \\[5pt]
x_1 &=& 6
\end{array}\)](https://mathjax.schullv.de/1b22ace855a606747a3acba26d9759c8beb0821b6afda4c391df9957b3a0935b?color=5a5a5a) Die Koordinaten des Schnittpunkts von
Die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse lauten
-Achse lauten 

b)
Mögliche Höhe der Pyramide untersuchen
Die Grundfläche  der Pyramide liegt vollständig in der Ebene
der Pyramide liegt vollständig in der Ebene  Die Höhe der Pyramide entspricht daher dem Abstand der Spitze zur Ebene
Die Höhe der Pyramide entspricht daher dem Abstand der Spitze zur Ebene 
Die Spitze liegt auf der Strecke Diese ist Teil der Geraden durch die beiden Punkte
Diese ist Teil der Geraden durch die beiden Punkte  und
und  Die Koordinaten von
Die Koordinaten von  kannst du anhand der Koordinaten von
kannst du anhand der Koordinaten von  und
und  zu
zu  bestimmen. Die Gerade durch
bestimmen. Die Gerade durch  und
und  kann daher durch folgende Gleichung beschrieben werden:
kann daher durch folgende Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
FG:\overrightarrow{x} &=& \overrightarrow{OF} + t\cdot \overrightarrow{FG} \\[5pt]
&=& \pmatrix{5\\0\\5} + t\cdot \pmatrix{0\\5\\0} \\[5pt]
&=& \pmatrix{5\\5t\\5} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fe969d3f51464877c92f38fcc508c65e8be63c3cd41e65cedbd772b0196b41db?color=5a5a5a) Überprüfe, ob es einen Punkt auf dieser Gerade gibt, der zur Ebene
Überprüfe, ob es einen Punkt auf dieser Gerade gibt, der zur Ebene  den Abstand
den Abstand  hat und ob dieser auf der Kante
hat und ob dieser auf der Kante  liegt.
1. Schritt: Punkt mit dem Abstand berechnen
Den Abstand eines Punktes zu einer Ebene kannst du mithilfe der Hesseschen Normalenform darstellen. Für die Hessesche Normalenform von
liegt.
1. Schritt: Punkt mit dem Abstand berechnen
Den Abstand eines Punktes zu einer Ebene kannst du mithilfe der Hesseschen Normalenform darstellen. Für die Hessesche Normalenform von  folgt:
folgt:
![\(\begin{array}[t]{rll}
& \dfrac{5x_1+4x_2+5x_3-30 }{ \left|\pmatrix{5\\4\\5} \right| } &=& 0 \\[5pt]
& \dfrac{5x_1+4x_2+5x_3-30 }{ \sqrt{5^2 +4^2 +5^2}} &=& 0 \\[5pt]
& \dfrac{5x_1+4x_2+5x_3-30 }{ \sqrt{66}} &=& 0
\end{array}\)](https://mathjax.schullv.de/b67a29a1fa44ae85ba8d93d82f3bcd1b1c10d763fc57fd8fd2c62d4474fdd7ef?color=5a5a5a) Der Abstand eines Punkts
Der Abstand eines Punkts  zu
zu  beträgt also:
beträgt also:
 Einsetzen der Koordinaten der Punkte von
Einsetzen der Koordinaten der Punkte von  liefert:
liefert:
![\(\begin{array}[t]{rll}
\dfrac{\left|5x_1+4x_2+5x_3 -30 \right| }{ \sqrt{66}} &=& \dfrac{18}{\sqrt{66}} \\[5pt]
\dfrac{\left|5\cdot 5 +4\cdot 5t +5\cdot 5 -30 \right| }{ \sqrt{66}} &=&\dfrac{18}{\sqrt{66}} \\[5pt]
\dfrac{\left|20+20t \right| }{ \sqrt{66}} &=& \dfrac{18}{\sqrt{66}} \\[5pt]
\left|20+20t \right| &=& 18
\end{array}\)](https://mathjax.schullv.de/368ac82db9196c04af71b6ae7c50c3c1fe3a449448f320aaa54be40043ddb937?color=5a5a5a) Aufgrund des Betrags kann nun
Aufgrund des Betrags kann nun  und
und  möglich sein:
möglich sein:
![\(\begin{array}[t]{rll}
20 + 20t_1 &=& 18 &\quad \scriptsize \mid\; -20\\[5pt]
20t_1 &=& -2 &\quad \scriptsize \mid\;:20 \\[5pt]
t_1 &=& -0,1 \\[5pt]
20 + 20t_2 &=& -18 &\quad \scriptsize \mid\; -20\\[5pt]
20t_2 &=& -38 &\quad \scriptsize \mid\;:20 \\[5pt]
t_2 &=& -1,9 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a10c6bb7e8404c0effbb0cf83ff53322d9057a8d684284bdf83f4468194e691c?color=5a5a5a) 2. Schritt: Lage auf der Kante überprüfen
Die Punkte auf der Geraden durch
2. Schritt: Lage auf der Kante überprüfen
Die Punkte auf der Geraden durch  und
und  mit der Gleichung
mit der Gleichung  liegen für
liegen für  zwischen den Punkten
zwischen den Punkten  und
und  also auf der Strecke
also auf der Strecke  Für andere Werte von
Für andere Werte von  liegen die Punkte nicht auf der Strecke
liegen die Punkte nicht auf der Strecke  Beide Werte von
Beide Werte von  die oben berechnet wurden, sind negativ. Die zugehörigen Punkte mit dem Abstand
die oben berechnet wurden, sind negativ. Die zugehörigen Punkte mit dem Abstand  zu
zu  liegen nicht auf der Strecke
liegen nicht auf der Strecke 
Die Pyramide kann also nicht die Höhe besitzen.
besitzen.
Die Spitze liegt auf der Strecke
Die Pyramide kann also nicht die Höhe
c)
Lage der Geraden begründen
Damit eine Gerade in der Ebene mit der Gleichung  liegt, muss die
liegt, muss die  -Koordinate jedes Punktes auf dieser Geraden
-Koordinate jedes Punktes auf dieser Geraden  sein. Dazu muss die
sein. Dazu muss die  -Koordinate des Richtungsvektors Null sein.
Bei der Geradenschar
-Koordinate des Richtungsvektors Null sein.
Bei der Geradenschar  ist die
ist die  -Koordinate des Richtungsvektors
-Koordinate des Richtungsvektors  Diese kann also in keinem Fall Null werden. Daher liegt keine der Geraden
Diese kann also in keinem Fall Null werden. Daher liegt keine der Geraden  in der Ebene mit der Gleichung
in der Ebene mit der Gleichung  Zugehörigkeit zur Schar überprüfen
Damit die Schnittgerade von
Zugehörigkeit zur Schar überprüfen
Damit die Schnittgerade von  und
und  zur Schar
zur Schar  gehört, muss es einen Wert von
gehört, muss es einen Wert von  geben, für den
geben, für den  in
in  und in
und in  liegt.
liegt.
Überprüfe also zunächst, ob der Stützpunkt von in
in  und in
und in  liegt:
liegt:
![\(\begin{array}[t]{rll}
5x_1 +4x_2 +5x_3 &=& 30 \\[5pt]
5\cdot 2,5 + 4\cdot 0 +5\cdot 3,5 &=& 30 \\[5pt]
30 &=& 30
\end{array}\)](https://mathjax.schullv.de/59738368121744d08d533a602fe2524da95190f1b6a2cf5a8c01f626c187f7fb?color=5a5a5a) Der Stützpunkt
Der Stützpunkt  von
von  liegt also in der Ebene
liegt also in der Ebene 
![\(\begin{array}[t]{rll}
U:\, -5x_1 +4x_2 +5x_3 &=& 5 \\[5pt]
-5\cdot 2,5 + 4\cdot 0 +5\cdot 3,5 &=& 5 \\[5pt]
5 &=& 5
\end{array}\)](https://mathjax.schullv.de/c5815731f4cf4bfa773dae9135bc1cd379c2a79ead24602e414a2d3779eef4f8?color=5a5a5a) Der Stützpunkt
Der Stützpunkt  von
von  liegt also ebenfalls in der Ebene
liegt also ebenfalls in der Ebene  Damit eine Gerade
Damit eine Gerade  in der Ebene
in der Ebene  bzw.
bzw.  liegt, muss sie zusätzlich parallel zu diesen Ebenen verlaufen. Dazu muss ihr Richtungsvektor senkrecht zu den Normalenvektoren von
liegt, muss sie zusätzlich parallel zu diesen Ebenen verlaufen. Dazu muss ihr Richtungsvektor senkrecht zu den Normalenvektoren von  und
und  verlaufen. Überprüfe also das Skalarprodukt:
Ebene
verlaufen. Überprüfe also das Skalarprodukt:
Ebene 
![\(\begin{array}[t]{rll}
\overrightarrow{r}_{g_a}\circ \overrightarrow{n}_T &=& 0 \\[5pt]
\pmatrix{0\\-10a \\\frac{2}{a}} \circ \pmatrix{5\\4\\5} &=& 0 \\[5pt]
0\cdot 5 -10a\cdot 4 +\frac{2}{a}\cdot 5 &=& 0 \\[5pt]
-40a +\frac{10}{a} &=& 0 \quad \scriptsize \mid\; \cdot a \\[5pt]
-40a^2 +10 &=& 0 \quad \scriptsize \mid\;-10 \\[5pt]
10 &=& 40a^2 \quad \scriptsize \mid\;:40 \\[5pt]
0,25 &=& a^2 \\[5pt]
a^2 &=& 0,25 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4ab045b48eed8cd83774322d69f45f28291979a1c44eb815ca1612335ee0cc3b?color=5a5a5a) Daraus folgt:
Daraus folgt:  und
und  Ebene
Ebene 
![\(\begin{array}[t]{rll}
\overrightarrow{r}_{g_a}\circ \overrightarrow{n}_U &=& 0 \\[5pt]
\pmatrix{0\\-10a \\\frac{2}{a}} \circ \pmatrix{-5\\4\\5} &=& 0 \\[5pt]
0\cdot (-5) -10a\cdot 4 +\frac{2}{a}\cdot 5 &=& 0 \\[5pt]
-40a +\frac{10}{a} &=& 0 \quad \scriptsize \mid\; \cdot a \\[5pt]
-40a^2 +10 &=& 0 \quad \scriptsize \mid\;+40a^2 \\[5pt]
10 &=& 40a^2 \quad \scriptsize \mid\;:40 \\[5pt]
0,25 &=& a^2\\[5pt]
a^2 &=& 0,25 \\[5pt]
a_1 &=& 0,5 \\[5pt]
a_2 &=& -0,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c4fc0edf1198e63b841dc51439021431fb70ccd8952b1044e5e463b4724ff68a?color=5a5a5a) Da
Da  vorgegeben ist, bleibt nur
vorgegeben ist, bleibt nur  als mögliche Lösung.
Die Gerade
als mögliche Lösung.
Die Gerade  mit
mit  liegt also in
liegt also in  und in
und in  Sie beschreibt damit die Schnittgerade dieser beiden Ebenen. Die Schnittgerade von
Sie beschreibt damit die Schnittgerade dieser beiden Ebenen. Die Schnittgerade von  und
und  ist also Teil der Geradenschar
ist also Teil der Geradenschar 
Überprüfe also zunächst, ob der Stützpunkt von