Pflichtteil

Aufgabe 1

Bilde die Ableitung der Funktion $f$ mit $f(x)=\left(4+\mathrm e^{3x}\right)^{5}$ .

(2 VP)

Aufgabe 2

Berechne das Integral $\mathop{\displaystyle\int}\limits_{0}^{\pi}\left(4x-\sin\left(\frac{1}{2}x\right)\right)\mathrm dx$ .

(2 VP)

Aufgabe 3

Löse die Gleichung $\left(x^{3}-3x\right)\cdot\left(\mathrm{e}^{2x}-5\right)=0$ .

(3 VP)

Aufgabe 4

Der Graph einer ganzrationalen Funktion $f$ dritten Grades hat im Ursprung einen Hochpunkt und an der Stelle $x=2$ die Tangente mit der Gleichung $y=4x-12$ .
Bestimme eine Funktionsgleichung von $f$ .

(4 VP)

Aufgabe 5

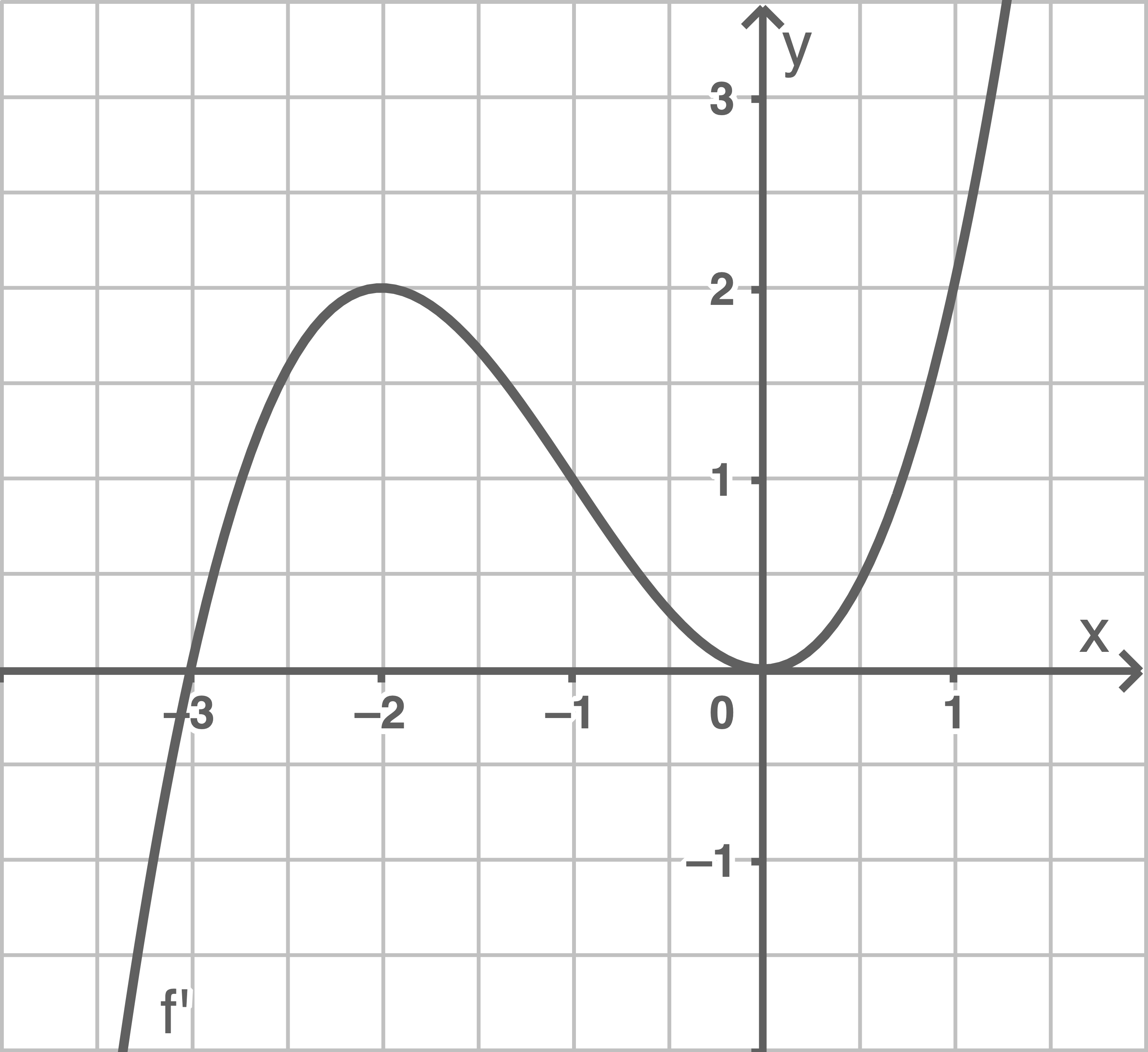
Die Abbildung zeigt den Graphen der Ableitungsfunktion $\(f$ einer ganzrationalen Funktion $f$ .
Entscheide, ob die folgenden Aussagen wahr oder falsch sind.
Begründe jeweils deine Antwort.

Der Graph von $f$ hat bei $x=-3$ einen Tiefpunkt.
$f(-2) \lt f(-1)$
$\(f$
Der Grad der Funktion $f$ ist mindestens vier.

Graf eines mathematischen Funktionsverlaufs mit Achsenbeschriftungen für x und y.

(5 VP)

Aufgabe 6

Gegeben sind die drei Punkte $A(4\mid0\mid4)$ , $B(0\mid4\mid4)$ und $C(6\mid6\mid2)$ .

Zeige, dass das Dreieck $ABC$ gleichschenklig ist.

Bestimme die Koordinaten eines Punktes, der das Dreieck $ABC$ zu einem Parallelogramm ergänzt.
Veranschauliche durch eine Skizze, wie viele solcher Punkte es gibt.

(4 VP)

Aufgabe 7

Gegeben ist die Ebene $E:\;4x_{1}+3x_{3}=12$ .

Stelle $E$ in einem Koordinatensystem dar.

Bestimme alle Punkte der $x_3$ -Achse, die von $E$ den Abstand 3 haben.

(3 VP)

Aufgabe 8

Ein Glücksrad hat drei farbige Sektoren, die beim einmaligen Drehen mit folgenden Wahrscheinlichkeiten angezeigt werden:

Rot: 20 %, Grün: 30 %, Blau: 50 %

Das Glücksrad wird $n$ -mal gedreht.
Die Zufallsvariable $X$ gibt an, wie oft die Farbe Rot angezeigt wird.

Begründe, dass $X$ binomialverteilt ist.

Die Tabelle zeigt einen Ausschnitt der Wahrscheinlichkeitsverteilung von $X$ :

$k$	$P(X=k)$
0	0,01
1	0,06
2	0,14
3	0,21
4	0,22
5	0,17
6	0,11
7	0,05
...	...

Bestimme die Wahrscheinlichkeit, dass mindestens dreimal Rot angezeigt wird.

Entscheide, welcher der folgenden Werte von $n$ der Tabelle zugrunde liegen kann: 20, 25 oder 30.
Begründe deine Entscheidung.

(4 VP)

Aufgabe 9

Mit $V=\pi\mathop{\displaystyle\int}\limits_{0}^{4}\left(4-\frac{1}{2}x\right)^{2}\mathrm dx$ wird der Rauminhalt eines Körpers berechnet.

Skizziere diesen Sachverhalt und beschreibe den Körper.

(3 VP)

Lösung 1

Die gegebene Funktion ist eine verkettete Funktion. Es wird also die Kettenregel angewendet:

$\(\begin{array}{rll} f(x)&=& \left(4+ \mathrm e^{3x}\right)^5\\ f$

Lösung 2

Um das Integral zu berechnen, benötigst du eine Stammfunktion der Funktion $g$ mit $g(x) = 4x-\sin\left(\frac{x}{2}\right)$ .
Beachte den Hauptsatz der Integralrechnung.

Bilde also zunächst eine Stammfunktion $G$ und berechne anschließend das Integral.

1. Schritt: Stammfunktion

Um eine Stammfunktion zu bilden, beachte, dass eine Stammfunktion von $\sin(x)$ die Funktion $-\cos(x)$ ist und wende lineare Substitution an, da es sich bei $\sin\left(\frac{x}{2}\right)$ um eine Verkettung handelt:

$\begin{array}{rll} g(x)&=&4x-\sin\left(\frac{x}{2}\right)\\[5pt] G(x)&=&\frac{4}{2}\cdot x^2 + 2\cdot\cos\left(\frac{x}{2}\right)\\[5pt] G(x)&=&2\cdot x^2 + 2\cdot\cos\left(\frac{x}{2}\right)\\[5pt] \end{array}$

2. Schritt: Integral berechnen

Vollständigen Rechenweg anzeigen

$\displaystyle\int_{0}^{\pi} \left(4x -\sin\left(\frac{x}{2}\right) \right)\mathrm dx=2\pi^2-2$

Lösung 3

$\begin{array}{rlllll} x^3-3x&=&0\\ x(x^2-3)&=&0\\ \end{array}$

Nach dem Satz vom Nullprodukt folgt: $x_1=0$

$\begin{array}{rlllll} x^2-3&=&0& \scriptsize\mid\; +3\\ x^2&=&3& \scriptsize\mid\; \sqrt{\;}\\ \end{array}$

$x_2=\sqrt{3}$ , $x_3=-\sqrt{3}$

$\begin{array}{rlllll} \mathrm e^{2x}-5&=&0&\scriptsize\mid\; +5\\ \mathrm e^{2x}&=&5& \scriptsize\mid\; \ln(\;)\\ 2x&=&\ln(5)& \scriptsize\mid\; : 2\\ x_4 &=&\dfrac{\ln(5)}{2}\\ \end{array}$

$\mathbb{L}= \left\{0;\sqrt{3};-\sqrt{3};\dfrac{\ln(5)}{2} \right\}$

Lösung 4

$f(x)=a\cdot x^3 +b\cdot x^2 +c\cdot x +d$

$\(f$

$\(\begin{array}{rlll} \text{I}& f(0)&=& 0\\ \text{II}& f$

$\begin{array}{lrllll} \text{I} &a\cdot 0^3 +b\cdot 0^2 +c\cdot 0 +d = 0& \\ \text{II}& 3\cdot a\cdot 0^2 +2\cdot b\cdot 0 +c = 0 \\ \text{III}& 3\cdot a\cdot 2^2 +2\cdot b\cdot 2 +c = 4\\ \text{IV}& a\cdot 2^3 +b\cdot 2^2 +c\cdot 2 +d = -4 \\ \end{array}$

Aus den ersten beiden Gleichungen folgt $c =0$ und $d =0$ .

$\begin{array}{lrllll} \text{IIIa}& 12\cdot a + 4\cdot b&=&4 & \scriptsize\mid\; -4b\\ &12a&=&4-4b& \scriptsize\mid\; : 12\\ & a &=& \dfrac{1}{3}-\dfrac{1}{3}b \\[5pt] \text{IVa}& 8\cdot a +4\cdot b &=& -4& \scriptsize\mid\; -8a\\ & 4\cdot b &=& -4-8a &\scriptsize\mid\; :4 \\ & b &=& -1-2a & \\ \end{array}$

$b$ in $\text{IIIa }$ :

$\begin{array}{rllll} a&=&\dfrac{1}{3}-\dfrac{1}{3}\left(-1-2a\right) \\[5pt] a&=&\dfrac{1}{3} +\dfrac{1}{3}+\frac{2}{3}a \mid\; -\frac{2}{3}a\\ \dfrac{1}{3}a &=& \dfrac{2}{3} \quad\scriptsize\mid \cdot 3 \\ a &=& 2 \end{array}$

$a$ in $\text{IVa }$ :

$b = -1-2\cdot 2 = -5$

$f(x) = 2 x^3 -5\dot x^2$

Lösung 5

Für diese Aufgabe ist es wichtig, dass du weißt, dass die erste Ableitungsfunktion $\(f$ einer Funktion $f$ die Steigung des Graphen von $f$ beschreibt.

Überprüfe hierzu, ob sowohl notwendiges Kriterium als auch hinreichendes Kriterium für einen Tiefpunkt erfüllt sind:

Der Abbildung kannst du entnehmen, dass $f‘$ bei $x =-3$ eine Nullstelle besitzt. Daher ist das notwendige Kriterium erfüllt.

Du kannst der Abbildung auch entnehmen, dass $f‘$ für Werte kleiner als $-3$ negative Werte und für Werte direkt nach $x =-3$ positive Werte annimmt. Es liegt also ein Vorzeichenwechsel der ersten Ableitung von $-$ zu $+$ vor. Damit ist auch das hinreichende Kriterium für einen Tiefpunkt erfüllt.

Die erste Aussage ist wahr.

Damit diese Aussage gilt, muss die Steigung zwischen den beiden Stellen $-2$ und $-1$ positiv sein. Der Abbildung kannst du entnehmen, dass der Graph von $f‘$ in diesem Bereich oberhalb der $x$ -Achse verläuft. Die Steigung ist also positiv.

Die zweite Aussage ist wahr.

Der Abbildung kannst du entnehmen, dass $f‘(-2) = 2$ gilt.Zudem kannst du sehen, dass der Graph von $f‘$ an der Stelle $x =-2$ einen Hochpunkt besitzt. Wegen des notwendigen Kriteriums für Hochpunkte muss also die zweite Ableitung $f‘‘$ an dieser Stelle eine Nullstelle besitzen. Damit folgt: $f‘‘(-2) +f‘(-2) = 0 +2 = 2 \lt 1$

Die dritte Aussage ist falsch.

Du kannst sehen, dass der Graph von $f‘$ mindestens zwei Extrempunkte besitzt. Dies bedeutet, dass $f‘$ mindestens den Grad drei haben muss. Da $f‘$ die Ableitung von $f$ und damit auf jeden Fall einen Grad weniger besitzt, muss $f$ mindestens den Grad vier haben.

Die vierte Aussage ist wahr.

Lösung 6

Ein Dreieck ist gleichschenklig, wenn mindestens zwei der Seiten gleich lang sind. Um das zu zeigen, wird jeweils der Betrag der Verbindungsvektoren $\overrightarrow{AB}$ , $\overrightarrow{AC}$ und $\overrightarrow{BC}$ berechnet:

$\left|\overrightarrow{AB} \right| = \left|\overrightarrow{OB} - \overrightarrow{OA} \right| = \left|\begin{pmatrix}-4\\4\\0 \end{pmatrix} \right|\,$ $= \sqrt{(-4)^2+4^2+0^2} = \sqrt{32}$

$\left|\overrightarrow{AC} \right| = \left|\overrightarrow{OC} - \overrightarrow{OA} \right| = \left|\begin{pmatrix}2\\6\\-2 \end{pmatrix} \right|\,$ $= \sqrt{2^2+6^2+(-2)^2} = \sqrt{44}$

$\left|\overrightarrow{BC} \right| = \left|\overrightarrow{OC} - \overrightarrow{OB} \right| = \left|\begin{pmatrix}6\\2\\-2 \end{pmatrix} \right|\,$ $= \sqrt{6^2+2^2+(-2)^2} = \sqrt{44}$

Da $\left|\overrightarrow{AC} \right| = \left|\overrightarrow{BC} \right|$ gilt, ist das Dreieck $ABC$ gleichschenklig.

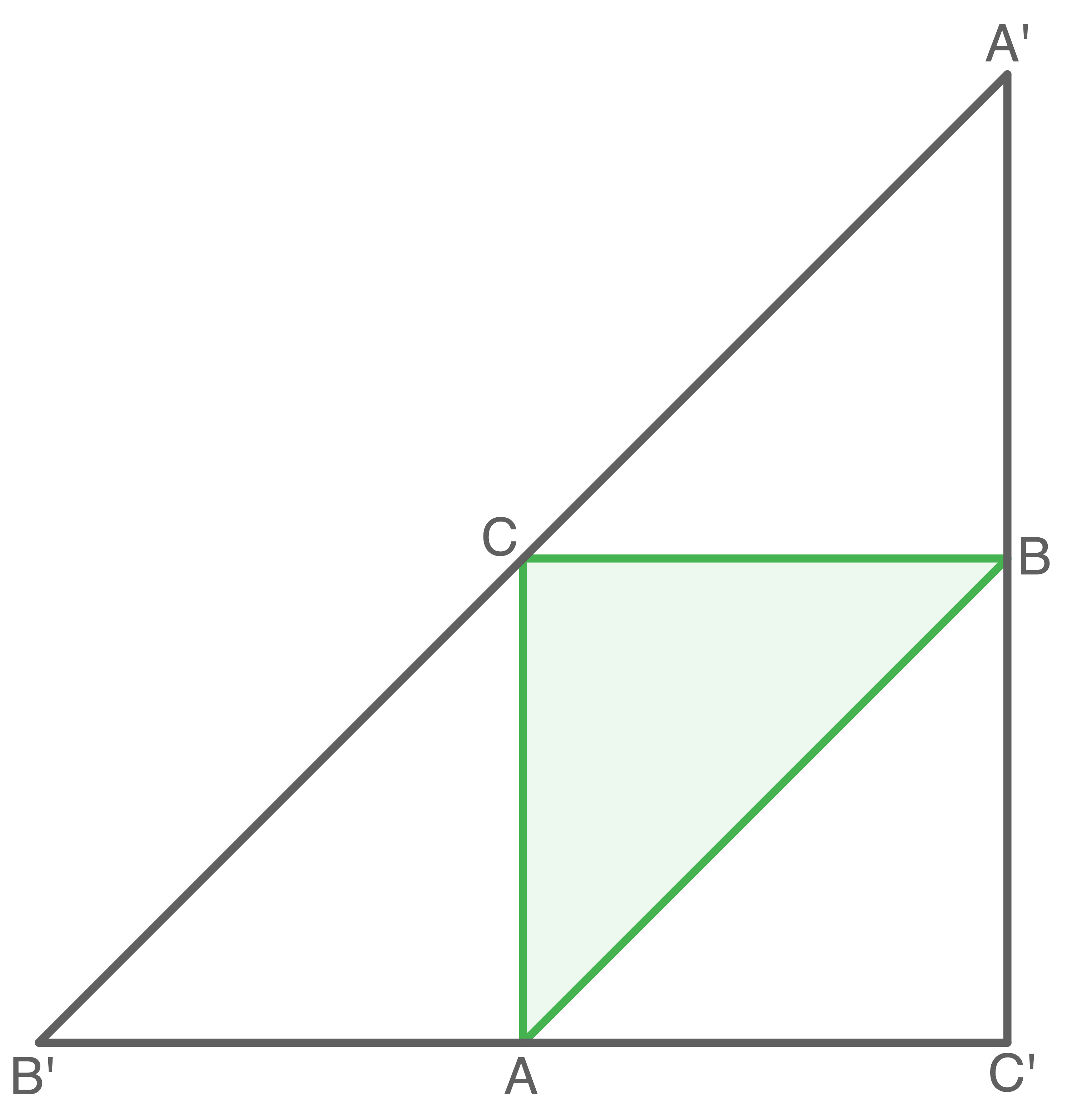
Geometrische Darstellung eines rechtwinkligen Dreiecks mit beschrifteten Punkten und einem grünen Rechteck.

Es gibt also drei mögliche Punkte, die das Dreieck $ABC$ zu einem Parallelogramm ergänzen. $\(\overrightarrow{OC$ $= \begin{pmatrix}4\\0\\4 \end{pmatrix} - \begin{pmatrix}6\\2\\-2 \end{pmatrix} = \begin{pmatrix}-2\\-2\\6 \end{pmatrix}$

Der Punkt $\(C$ ergänzt das Dreieck $ABC$ zu einem Parallelogramm.

Lösung 7

Schnittstellen bestimmen

Schnittstelle $x_1$ -Achse: $x_2 =0,$ $x_3=0$

$4x_1+3\cdot 0 = 12$ , daraus folgt $4x_1 = 12$ , also $x_1 = 3$

Schnittstelle $x_2$ -Achse: $x_1=0,$ $x_3=0$

$4\cdot0 + 3\cdot 0 = 12$

Da diese Gleichung keine Lösung besitzt, schneidet $E$ die $x_2$ -Achse nicht und liegt somit parallel zu dieser.

Schnittstelle $x_3$ -Achse: $x_1 =0,$ $x_2 =0$

$4\cdot0 + 3\cdot x_3 = 12,$ daraus folgt $3x_3 = 12,$ also $x_3 = 4$

Ebene darstellen

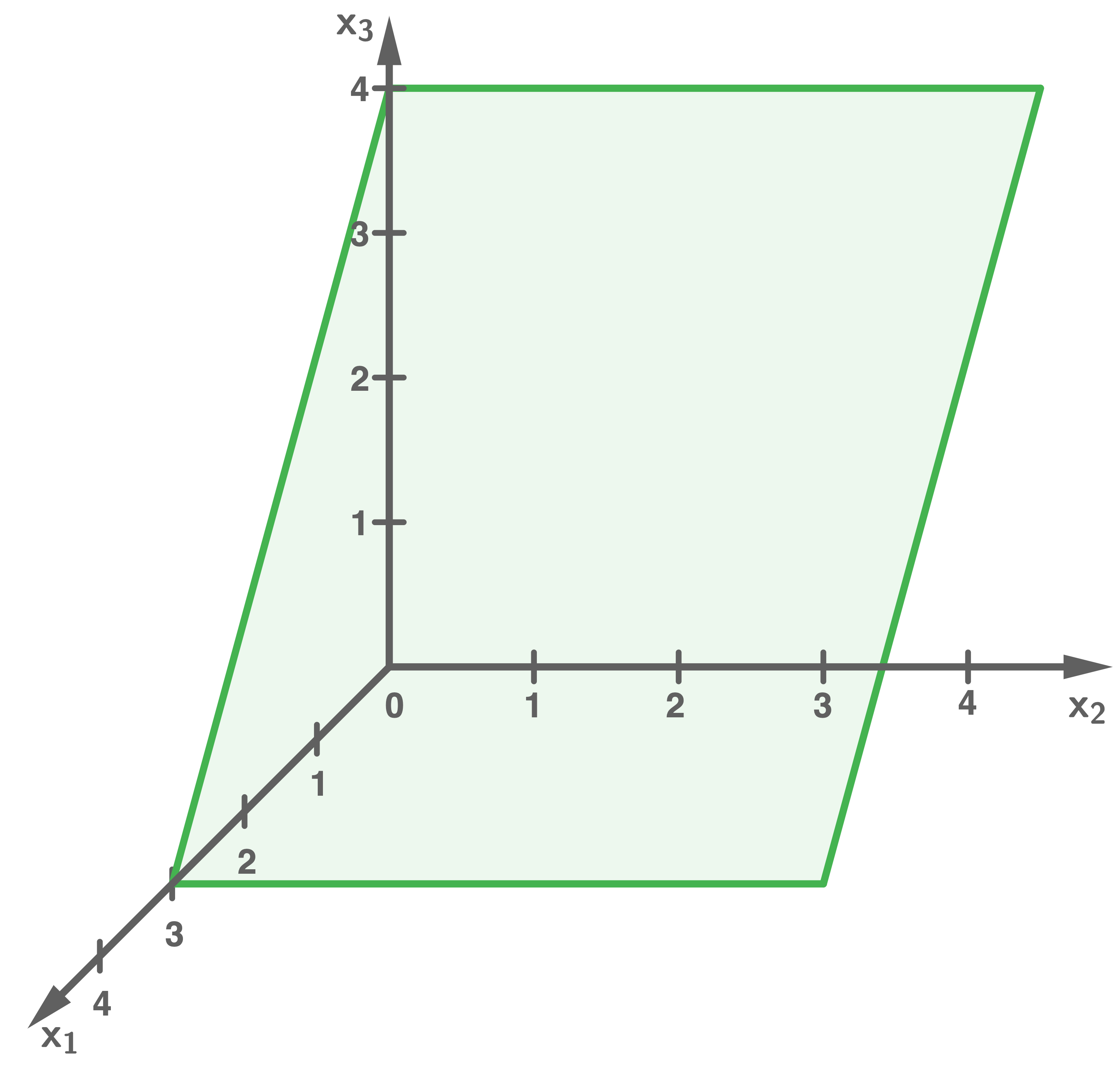
3D-Darstellung eines geometrischen Körpers im Raum mit Achsen x1, x2 und x3.

Die $x_3$ -Achse entspricht der Geraden mit der Gleichung $g: \overrightarrow{x} = t\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}.$ Jeder Punkt auf dieser Gerade hat die Koordinaten $\pmatrix{0\\0\\t}.$ Einsetzen dieser Punkte sowie einsetzen des Normalenvektors $\pmatrix{4\\0\\3}$ von $E$ in die Abstandsformel ergibt:

$d_t =\dfrac{\left|4\cdot 0 + 0 \cdot 0 +3 \cdot t -12\right|}{\sqrt{4^2+0^2+3^2}}\,$ $=\dfrac{\left|3t-12\right|}{5}$

Der Abstand soll $3$ betragen:

$\begin{array}[t]{rll} d_t&=&3 \\[5pt] \dfrac{\left|3t-12\right|}{5}&=&3 \quad \scriptsize \mid\;\; \cdot 5 \\[5pt] \left|3t-12\right| &=&15 \\[5pt] \end{array}$

Daraus folgen zwei Gleichungen:

$\begin{array}[t]{rll} 3t-12&=&15 \quad \scriptsize \mid\;\; +12 \\[5pt] 3t &=&27 \quad \scriptsize \mid\;\; :3\\[5pt] t_1 &=&9 \end{array}$

$\begin{array}[t]{rll} 3t-12&=&-15 \quad \scriptsize \mid\;\; +12 \\[5pt] 3t &=&-3 \quad \scriptsize \mid\;\; :3\\[5pt] t_2 &=&-1 \end{array}$

Die Punkte $A(0\mid\; 0\mid\; 9)$ und $B(0\mid\;0\mid\; -1)$ liegen auf der $x_3$ -Achse und haben von $E$ den Abstand $3$ .

Lösung 8

Bei jedem Dreh werden nur zwei Ergebnisse unterschieden: Es wird Rot angezeigt oder es wird nicht rot angezeigt.
Da bei jedem Dreh das gleiche Glücksrad verwendet wird, ist die Wahrscheinlichkeit für Rot bei jedem Dreh gleich.
Die Ergebnisse der einzelnen Drehungen sind voneinander abhängig.

Das Gegenereignis wird betrachtet:

$P(X\geq 3)$ $= 1- (P(X=0) + P(X=1) + P(X=2))$ $= 1- (0,01 + 0,06 + 0,14)$ $= 0,79$

Mit einer Wahrscheinlichkeit von $0,79 = 79\,\%$ wird mindestens dreimal Rot angezeigt.

Für die binomialverteilte Zufallsgröße $X$ gilt $p=0,2.$ Für die verschiedenen Werte von $n$ ergeben sich mit der zugehörigen Formel folgende Erwartungswerte:

$n=20:\;$ $\mu = n\cdot p = 20 \cdot 0,2 = 4$

$n=25:\;$ $\mu = 25 \cdot 0,2 = 5$

$n=30:\;$ $\mu = 30 \cdot 0,2 = 6$

Der Erwartungswert ist der Wert $k$ mit der höchsten Wahrscheinlichkeit. In der Tabelle besitzt $k=4$ die höchste Wahrscheinlichkeit. Also kann nur $n=20$ der Tabelle zugrunde liegen.

Lösung 9

$\blacktriangleright$ Sachverhalt skizzieren

Hier wird das Volumen eines Rotationskörpers berechnet. Dieser entsteht durch Rotation des Graphen der Funktion $f$ mit der Gleichung $f(x) = 4-\frac{1}{2}x$ um die $x$ -Achse. Skizziere also den Graphen dieser Funktion. Anhand der Skizze kannst du dann auch erkennen um was für einen Körper es sich handelt. Es ergibt sich folgende Skizze:

Diagramm mit einer diagonalen Linie in einem Koordinatensystem.

Anhand der Skizze kannst du erkennen, dass es sich bei dem Körper, der durch die Rotation entsteht, um einen Kegel handelt. Die Spitze befindet sich an der Nullstelle von $f$ im Punkt $(8\mid\;0)$ . Da das Integral allerdings nur von $0$ bis $4$ geht, wird dadurch auch nur der Rotationskörper bis zur Gerade zu $x=4$ beschrieben. Es entsteht also ein Kegelstumpf.