Wahlteil A2
Aufgabe A 2.1
Die Abbildung zeigt den Graphen der Funktion  mit
mit  , die für
, die für  die momentane Änderungsrate des Wasservolumens in einem Becken beschreibt (
die momentane Änderungsrate des Wasservolumens in einem Becken beschreibt ( in Stunden nach Beobachtungsbeginn,
in Stunden nach Beobachtungsbeginn,  in Kubikmeter pro Stunde).
in Kubikmeter pro Stunde).
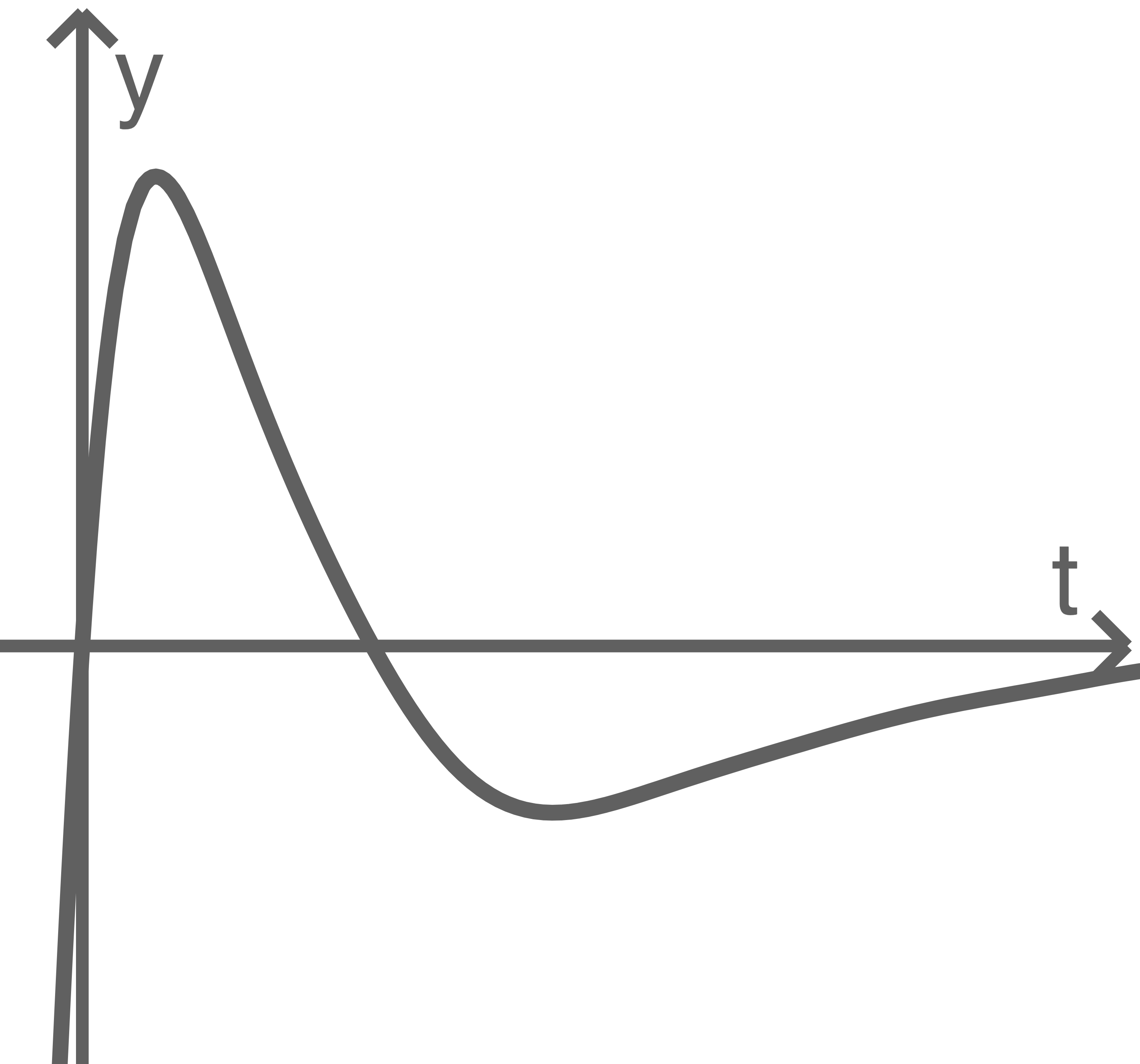
a)
Gib die momentane Änderungsrate des Wasservolumens eine Stunde nach Beobachtungsbeginn an.
Bestimme den Zeitpunkt, zu dem dieses Minimum angenommen wird. Teilergebnis:
Teilergebnis: 

Die Funktion
(0,5 VP)
Begründe, dass das Wasservolumen in den ersten beiden Stunden nach Beobachtungsbeginn niemals abnimmt.
(1,5 VP)
Die momentane Änderungsrate des Wasservolumens besitzt ein Minimum.
Bestimme den Zeitpunkt, zu dem dieses Minimum angenommen wird.
(2,5 VP)
b)
Ermittle das Wasservolumen, das sich zu Beobachtungsbeginn im Becken befand.
(1,5 VP)
Es gibt einen 45-Minuten-Zeitraum, in welchem das Wasservolumen um genau einen Kubikmeter zunimmt. Gib eine Gleichung an, deren Lösung den Beginn dieses Zeitraums darstellt.
(1 VP)
c)
Über eine Schaltuhr kann ein Zeitpunkt  gewählt werden, so dass die momentane Änderungsrate des Wasservolumens nur bis
gewählt werden, so dass die momentane Änderungsrate des Wasservolumens nur bis  durch die Funktion
durch die Funktion  beschrieben wird und danach konstant auf dem Wert
beschrieben wird und danach konstant auf dem Wert  bleibt. Zeige, dass
bleibt. Zeige, dass  nicht so gewählt werden kann, dass das Becken sieben Stunden nach Beobachtungsbeginn leer ist.
nicht so gewählt werden kann, dass das Becken sieben Stunden nach Beobachtungsbeginn leer ist.
(2 VP)
Für ein anderes Becken beschreiben die Funktion  die momentane Zuflussrate und die Funktion
die momentane Zuflussrate und die Funktion  die momentane Abflusrate des Wassers in Abhängigkeit von der Zeit
die momentane Abflusrate des Wassers in Abhängigkeit von der Zeit  (
( in Stunden nach Beobachtungsbeginn,
in Stunden nach Beobachtungsbeginn,  und
und  in Kubikmeter pro Stunde). Die Abbildung zeigt die Graphen der beiden Funktionen
in Kubikmeter pro Stunde). Die Abbildung zeigt die Graphen der beiden Funktionen  und
und 
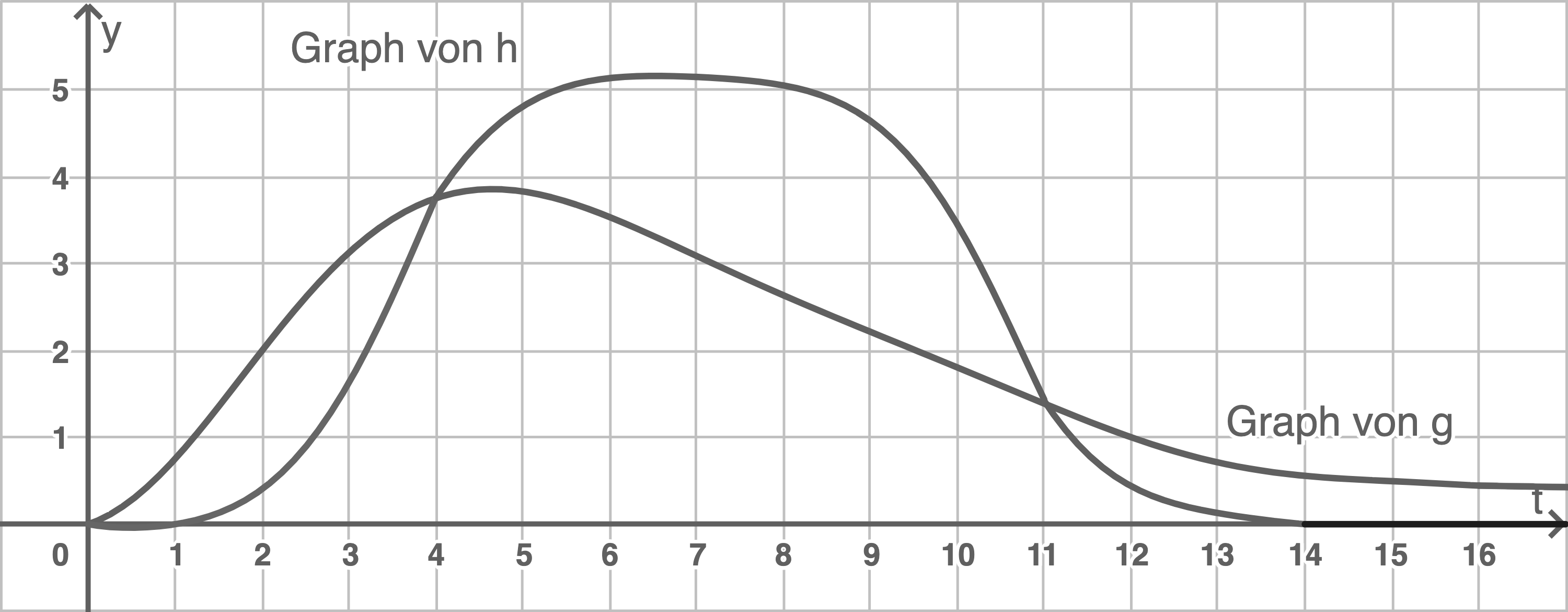
d)
Gib den Zeitraum an, in dem das Wasservolumen in diesem Becken abnimmt.
 gesammelt. Dieser ist zu Beobachtungsbeginn leer. Untersuche, ob das Wasser im Tank höher als
gesammelt. Dieser ist zu Beobachtungsbeginn leer. Untersuche, ob das Wasser im Tank höher als  steigt.
steigt.
(0,5 VP)
Das abfließende Wasser wird in einem quaderförmigen Tank mit der Grundfläche
(2 VP)
Entscheide, ob das Becken zu Beobachtungsbeginn leer war, und begründe deine Entscheidung.
(1,5 VP)
Aufgabe A 2.2
Für jede reelle Zahl
a)
Gib Gleichungen der Asymptoten des Graphen  an.
an.
 von
von  gilt:
gilt: 
 genau einen Extrempunkt besitzt, und untersuche, für welche Werte
genau einen Extrempunkt besitzt, und untersuche, für welche Werte
von ein Hochpunkt vorliegt.
ein Hochpunkt vorliegt.
(1 VP)
Weise nach, dass für die Ableitung
(1,5 VP)
Zeige, dass jeder Graph von
(2,5 VP)
b)
Jeder Graph  besitzt einen Punkt
besitzt einen Punkt  mit der folgenden Eigenschaft: Die Tangente im Punkt
mit der folgenden Eigenschaft: Die Tangente im Punkt  an
an  verläuft durch den Ursprung. Bestimme die
verläuft durch den Ursprung. Bestimme die  -Koordinate von
-Koordinate von 
(2 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung A 2.1
a)
Momentane Änderungsrate eine Stunde nach Beobachtungsbeginn:
![\(\begin{array}[t]{rll}
f(1)&=&\left(2\cdot1-1^2\right)\cdot \mathrm e^{2-1} &\ \\[5pt]
&=&1\cdot \mathrm e^1 &\ \\[5pt]
&=&\mathrm e &\ \\[5pt]
&\approx & 2,7
\end{array}\)](https://mathjax.schullv.de/b29c7256cce3af66033b971c9f5bb51e50c84d34b5367c3f7118eac799e6e04b?color=5a5a5a) Eine Stunde nach Beobachtungsbeginn beträgt die momentane Änderungsrate also
Eine Stunde nach Beobachtungsbeginn beträgt die momentane Änderungsrate also  Kubikmeter pro Stunde.
Begründung
Bestimmen der Nullstellen:
Kubikmeter pro Stunde.
Begründung
Bestimmen der Nullstellen:
![\(\begin{array}[t]{rll}
f(t)&=& 0 & \\[5pt]
\left(2t-t^2\right)\cdot \mathrm e^{2-t}&=&0 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/68603f2ced8890ea7937f51c57ff15c910cb32bfacea031d886982cef7c7340d?color=5a5a5a) Es gilt
Es gilt  und somit folgt mit dem Satz vom Nullprodukt
und somit folgt mit dem Satz vom Nullprodukt  Daraus ergeben sich die Nullstellen
Daraus ergeben sich die Nullstellen  ud
ud  Der Abbildung wird entnommen, dass
Der Abbildung wird entnommen, dass  für
für  also nimmt das Wasservolumen in den ersten beiden Stunden nie ab.
Zeitpunkt des Minimums bestimmen
Notwendige Bedingung für Extremstellen anwenden:
also nimmt das Wasservolumen in den ersten beiden Stunden nie ab.
Zeitpunkt des Minimums bestimmen
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/87be97f85db9b90ff4f15729ec6af7430cf8382797abfb9f80cd7e9fb633a309?color=5a5a5a) Es gilt stets
Es gilt stets  Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt 
 -Formel anwenden:
-Formel anwenden:
![\(\begin{array}[t]{rll}
t_{1;2}&=&-\dfrac{-4}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-2}& \\[5pt]
t_{1;2}&=&2 \pm \sqrt{2}& \\[5pt]
t_1&=&2 + \sqrt{2}& \\[5pt]
t_2&=&2 - \sqrt{2}
\end{array}\)](https://mathjax.schullv.de/cdd55d9700cc8378cac6c20f45eea6445ff3c631a7563bb6d948548d36e5c7c4?color=5a5a5a) Mit der Abbildung ergibt sich, dass
Mit der Abbildung ergibt sich, dass  die Stelle ist, an der das Minimum angenommen wird. Auf die hinreichende Bedingung für Extremstellen kann somit verzichtet werden. Etwa 3,4 Stunden nach Beobachtungsbeginn nimmt die Änderungsrate des Wasservolumens ihr Minimum an.
die Stelle ist, an der das Minimum angenommen wird. Auf die hinreichende Bedingung für Extremstellen kann somit verzichtet werden. Etwa 3,4 Stunden nach Beobachtungsbeginn nimmt die Änderungsrate des Wasservolumens ihr Minimum an.
b)
Wasservolumen zu Beobachtungsbeginn
Gleichung angeben
45 Minuten entsprechen 0,75 Stunden.
Als Zeitraum ergibt sich ![\([t;t+0,75]\)](https://mathjax.schullv.de/81c1c4bbe94ee5949f6b49a99697140ff3515b1e454ee93065cee568aab459d9?color=5a5a5a)
c)
Da sich das Becken leeren soll, muss  gewählt werden, da nur in diesem Bereich die Änderungsrate negativ ist. Wenn das Becken 7 Stunden nach Beobachtungsbeginn leer sein soll, kann höchstens 5 Stunden lang Wasser abfließen. Da sich bis zu
gewählt werden, da nur in diesem Bereich die Änderungsrate negativ ist. Wenn das Becken 7 Stunden nach Beobachtungsbeginn leer sein soll, kann höchstens 5 Stunden lang Wasser abfließen. Da sich bis zu  genau
genau  Wasser im Becken gesammelt haben, müsste das Wasser in diesen 5 Stunden mit einer konstanten Geschwindigkeit von
Wasser im Becken gesammelt haben, müsste das Wasser in diesen 5 Stunden mit einer konstanten Geschwindigkeit von  abfließen.
Maximale Abflussrate bestimmen:
Da die Abflussrate zu keinem Zeitpunkt
abfließen.
Maximale Abflussrate bestimmen:
Da die Abflussrate zu keinem Zeitpunkt  erreicht und
erreicht und  , fließen für kein
, fließen für kein  innerhalb von
innerhalb von  Stunden
Stunden  Wasser ab.
Wasser ab.
d)
Zeitraum bestimmen
An den Schnittstellen der Graphen von  und
und  ist ablesbar, zu welchem Zeitpunkt sich Zufluss und Abfluss ausgleichen. Da zwischen
ist ablesbar, zu welchem Zeitpunkt sich Zufluss und Abfluss ausgleichen. Da zwischen  und
und  der Graph von
der Graph von  oberhalb des Graphen von
oberhalb des Graphen von  verläuft, nimmt in diesem Zeitraum das Wasservolumen ab.
Füllhöhe untersuchen
Da die Grundfläche des Tanks
verläuft, nimmt in diesem Zeitraum das Wasservolumen ab.
Füllhöhe untersuchen
Da die Grundfläche des Tanks  groß ist, würde dieser bei einer Füllhöhe von
groß ist, würde dieser bei einer Füllhöhe von  insgesamt
insgesamt  Wasser fassen.
Die Fläche unter dem Graph von
Wasser fassen.
Die Fläche unter dem Graph von  gibt die Menge des abgeflossenen Wassers an, wobei ein Kästchen einem Kubikmeter entspricht. Durch Abzählen lässt sich feststellen, dass der Flächeninhalt
gibt die Menge des abgeflossenen Wassers an, wobei ein Kästchen einem Kubikmeter entspricht. Durch Abzählen lässt sich feststellen, dass der Flächeninhalt  kleiner als
kleiner als  ist. Somit steigt das Wasser nicht bis zu einer Höhe von
ist. Somit steigt das Wasser nicht bis zu einer Höhe von  an.
an.
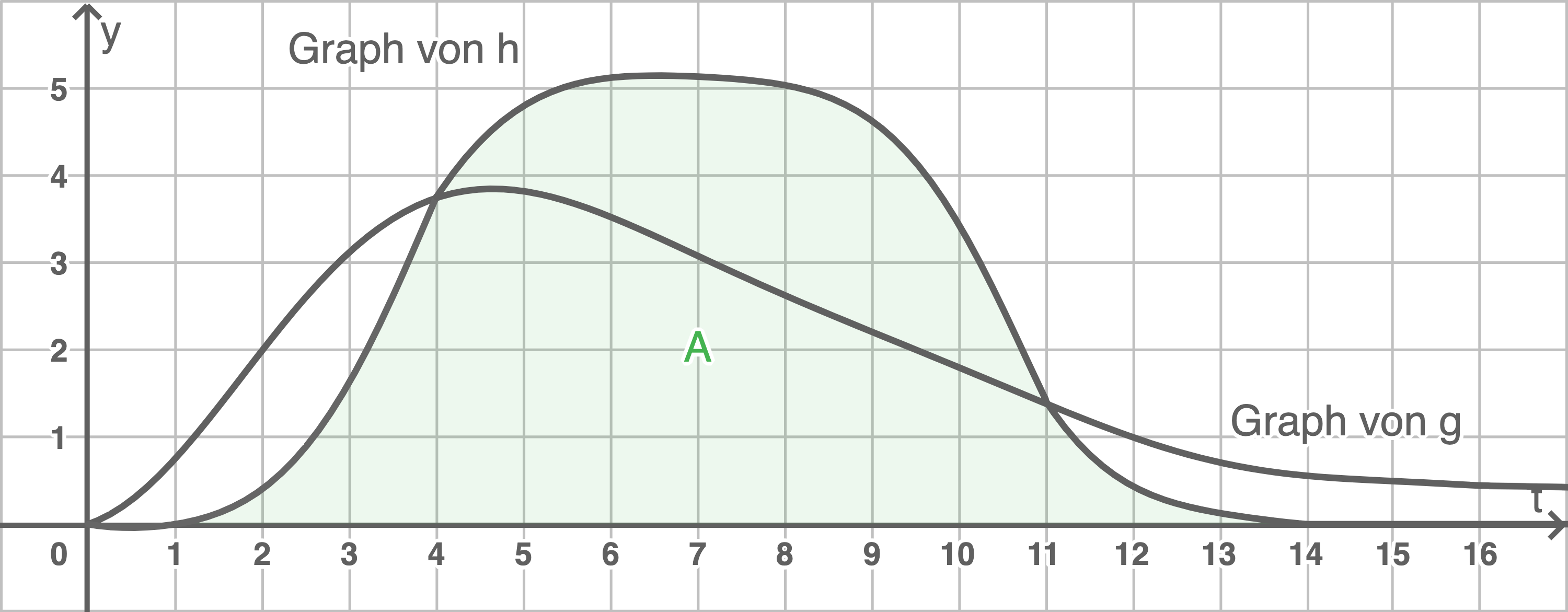 Füllhöhe des Beckens zu Beobachtungsbeginn
Da der Flächeninhalt der Fläche
Füllhöhe des Beckens zu Beobachtungsbeginn
Da der Flächeninhalt der Fläche  kleiner als der Inhalt der Fläche
kleiner als der Inhalt der Fläche  ist, fließt in den ersten 11 Stunden mehr Wasser ab als hinzu. Deshalb kann das Becken zu Beobachtungsbeginn nicht leer gewesen sein.
ist, fließt in den ersten 11 Stunden mehr Wasser ab als hinzu. Deshalb kann das Becken zu Beobachtungsbeginn nicht leer gewesen sein.
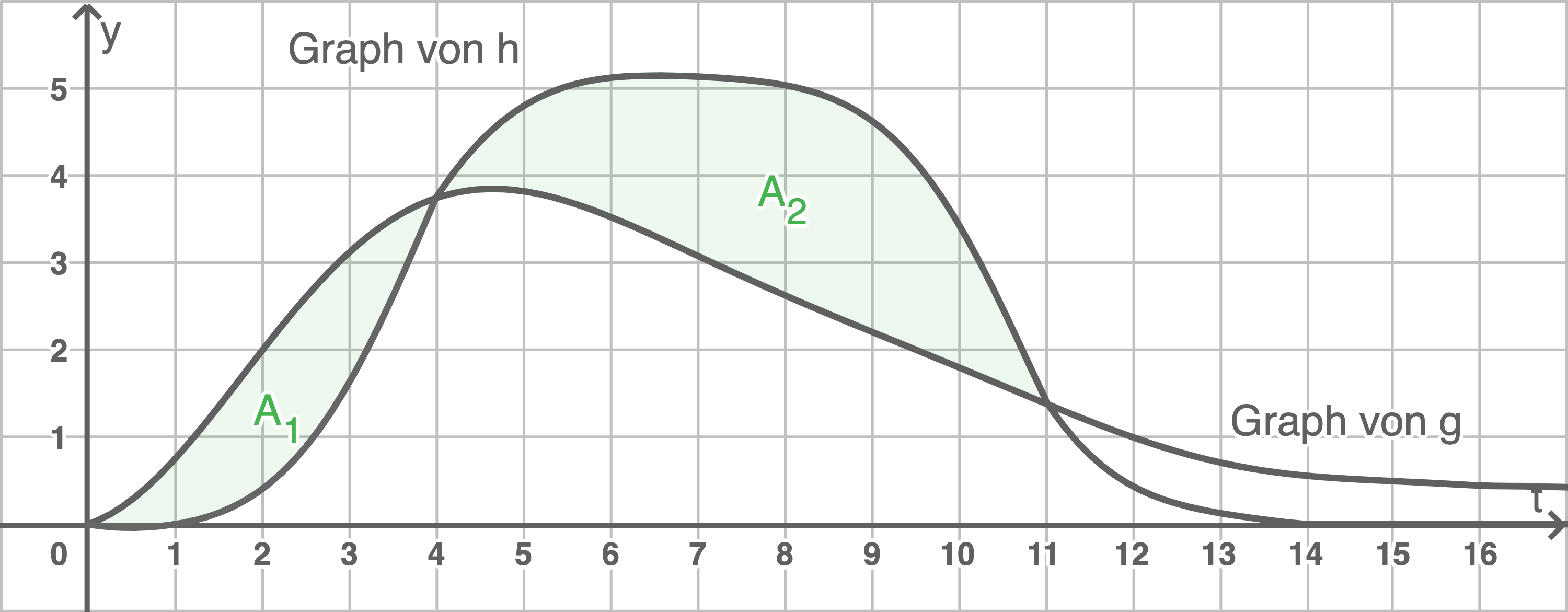


Lösung A 2.2
a)
Gleichungen der Asymptoten von  bestimmen
Aus der Definitionslücke von
bestimmen
Aus der Definitionslücke von  folgt die senkrechte Asymptote
folgt die senkrechte Asymptote  Durch das Betrachten des Grenzwerts von
Durch das Betrachten des Grenzwerts von  folgt: Für
folgt: Für  gilt
gilt  . Somit ist die waagereche Asymptote durch
. Somit ist die waagereche Asymptote durch  festgelegt.
Ableitung von
festgelegt.
Ableitung von  nachweisen
nachweisen
![\(\begin{array}[t]{rll}
k_a](https://mathjax.schullv.de/b25b5c20e4af75d53c401bd514dd3b33156a445e2f7ce6a0af327ce65ad4a286?color=5a5a5a) Extremstellen in Abhängigkeit von
Extremstellen in Abhängigkeit von  untersuchen
Notwendige Bedingung für Extremstellen anwenden:
untersuchen
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
k_a](https://mathjax.schullv.de/78c827257ddf90c524bd7804263c2ff04e6d65fcbc58aee281c6ed11d49aabec?color=5a5a5a) Jeder Graph
Jeder Graph  hat also einen einzigen Extrempunkt an der Stelle
hat also einen einzigen Extrempunkt an der Stelle  .
Überprüfen der hinreichenden Bedingung für Extremstellen:
.
Überprüfen der hinreichenden Bedingung für Extremstellen:

![\(\begin{array}[t]{rll}
k](https://mathjax.schullv.de/db64a3968e79a689fd1ce2583db403d8c19822af30975b5192253faa8d082a70?color=5a5a5a) Für
Für  besitzen alle Graphen
besitzen alle Graphen  mit
mit  einen Hochpunkt als Extrempunkt.
einen Hochpunkt als Extrempunkt.
b)