Analysis
Aufgabe 1A
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Abbildung 1 zeigt den Graphen von
Abbildung 1 zeigt den Graphen von  sowie den Punkt
sowie den Punkt 
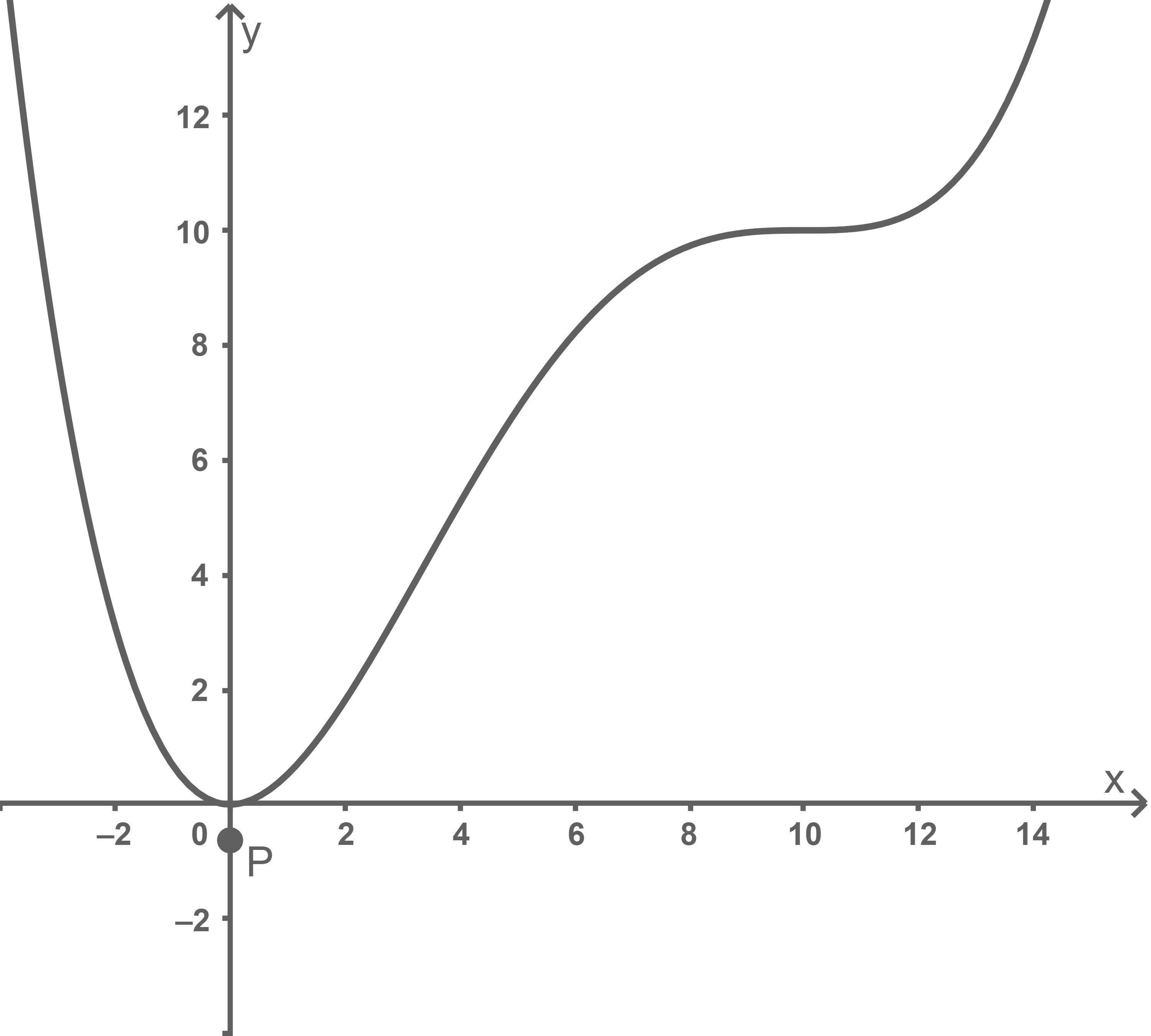
Abbildung 1
a)
Der Graph von  besitzt den Tiefpunkt
besitzt den Tiefpunkt  Zeige, dass der Graph von
Zeige, dass der Graph von  keine weiteren Extrempunkte besitzt.
keine weiteren Extrempunkte besitzt.
Die Gerade durch die Punkte
(4 BE)
b)
Ermittle eine Gleichung von  Weise rechnerisch nach, dass
Weise rechnerisch nach, dass  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist.
[Zur Kontrolle: Gleichung von
ist.
[Zur Kontrolle: Gleichung von  ]
]
(5 BE)
c)
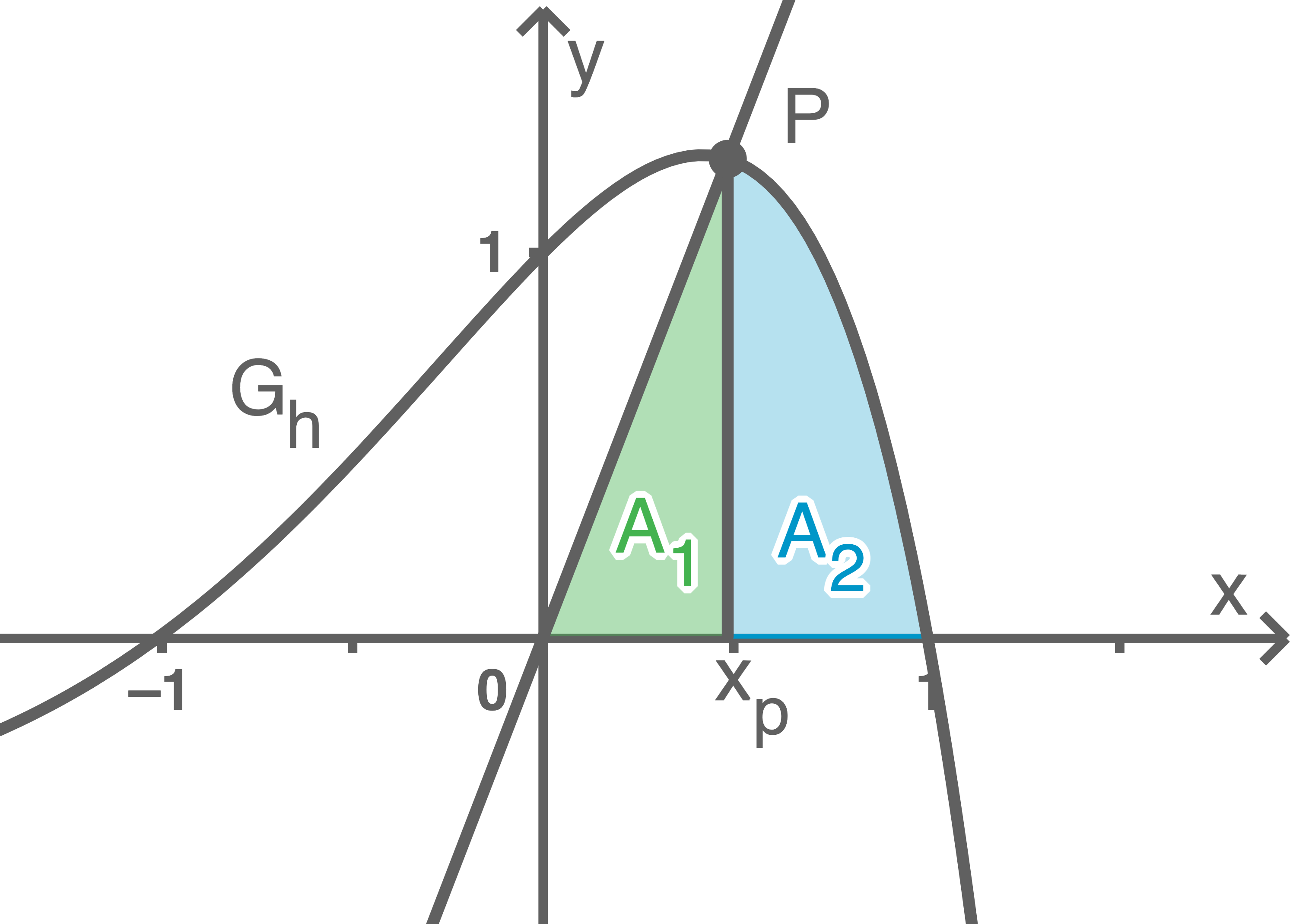
Der Graph von  und die Tangente
und die Tangente  schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
(6 BE)
d)
Der Graph der in  definierten Funktion
definierten Funktion  kann aus dem Graphen von
kann aus dem Graphen von  erzeugt werden. Der Punkt
erzeugt werden. Der Punkt  des Graphen von
des Graphen von  wird dabei aus dem Punkt
wird dabei aus dem Punkt  des Graphen von
des Graphen von  erzeugt und für alle
erzeugt und für alle  gilt
gilt  mit
mit  Gib in diesem Zusammenhang die Bedeutung von
Gib in diesem Zusammenhang die Bedeutung von  und
und  an und berechne die Werte von
an und berechne die Werte von  und
und 
(4 BE)
Zwei Radfahrer starten gleichzeitig nebeneinander. Die Geschwindigkeit von Radfahrer  wird in den ersten 10 Sekunden (s) nach dem Start durch die Funktion
wird in den ersten 10 Sekunden (s) nach dem Start durch die Funktion  mit
mit  beschrieben. Die Geschwindigkeit von Radfahrer
beschrieben. Die Geschwindigkeit von Radfahrer  wird in den ersten 12 Sekunden nach dem Start durch die in
wird in den ersten 12 Sekunden nach dem Start durch die in  definierte Funktion
definierte Funktion  mit
mit  beschrieben.
beschrieben.
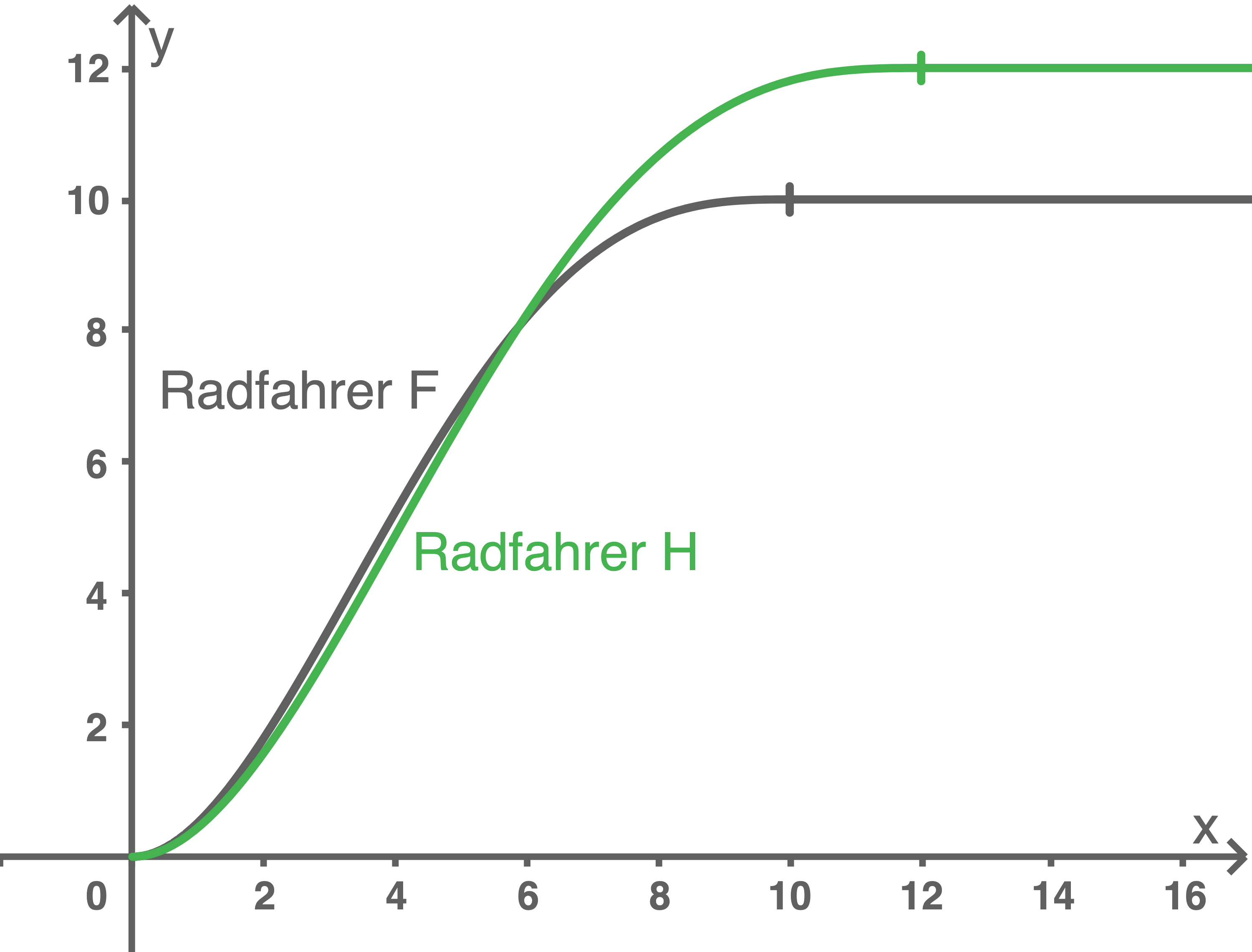
Abbildung 2
e)
Bestimme die Geschwindigkeit von Radfahrer  drei Sekunden nach dem Start sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von
drei Sekunden nach dem Start sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von  erreicht.
erreicht.
(4 BE)
f)
Nach den ersten 12 Sekunden fährt Radfahrer  mit konstanter Geschwindigkeit.
Gib diese konstante Geschwindigkeit an.
Zeige durch Rechnung, dass der zum Radfahrer
mit konstanter Geschwindigkeit.
Gib diese konstante Geschwindigkeit an.
Zeige durch Rechnung, dass der zum Radfahrer  gehörende Graph in der Abbildung 2 an der Stelle 12 eine waagerechte Tangente aufweist.
gehörende Graph in der Abbildung 2 an der Stelle 12 eine waagerechte Tangente aufweist.
Nach dem Start gibt es genau einen Zeitpunkt, zu dem die Geschwindigkeiten beider Radfahrer gleich groß sind. Im Modell wird dieser Zeitpunkt mit
(4 BE)
g)
Berechne 
(3 BE)
h)
Es gibt genau einen Zeitpunkt in den ersten 10 Sekunden nach dem Start, zu dem einer der beiden Radfahrer den anderen überholt.
Berechne, um wie viel Prozent die Geschwindigkeit des schnelleren Radfahrers die Geschwindigkeit des langsameren Radfahrers zum Zeitpunkt des Überholens übersteigt.
(5 BE)
Aufgabe 1B
Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in
a)
Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.
Bestimme den Zeitpunkt, zu dem die Wassertemperatur  beträgt.
beträgt.
(3 BE)
b)
Berechne die Werte der folgenden Terme und interpretiere diese im Sachzusammenhang:


(6 BE)
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
Ohne Nachweis kann verwendet werden:
bezeichnet.
Ohne Nachweis kann verwendet werden:

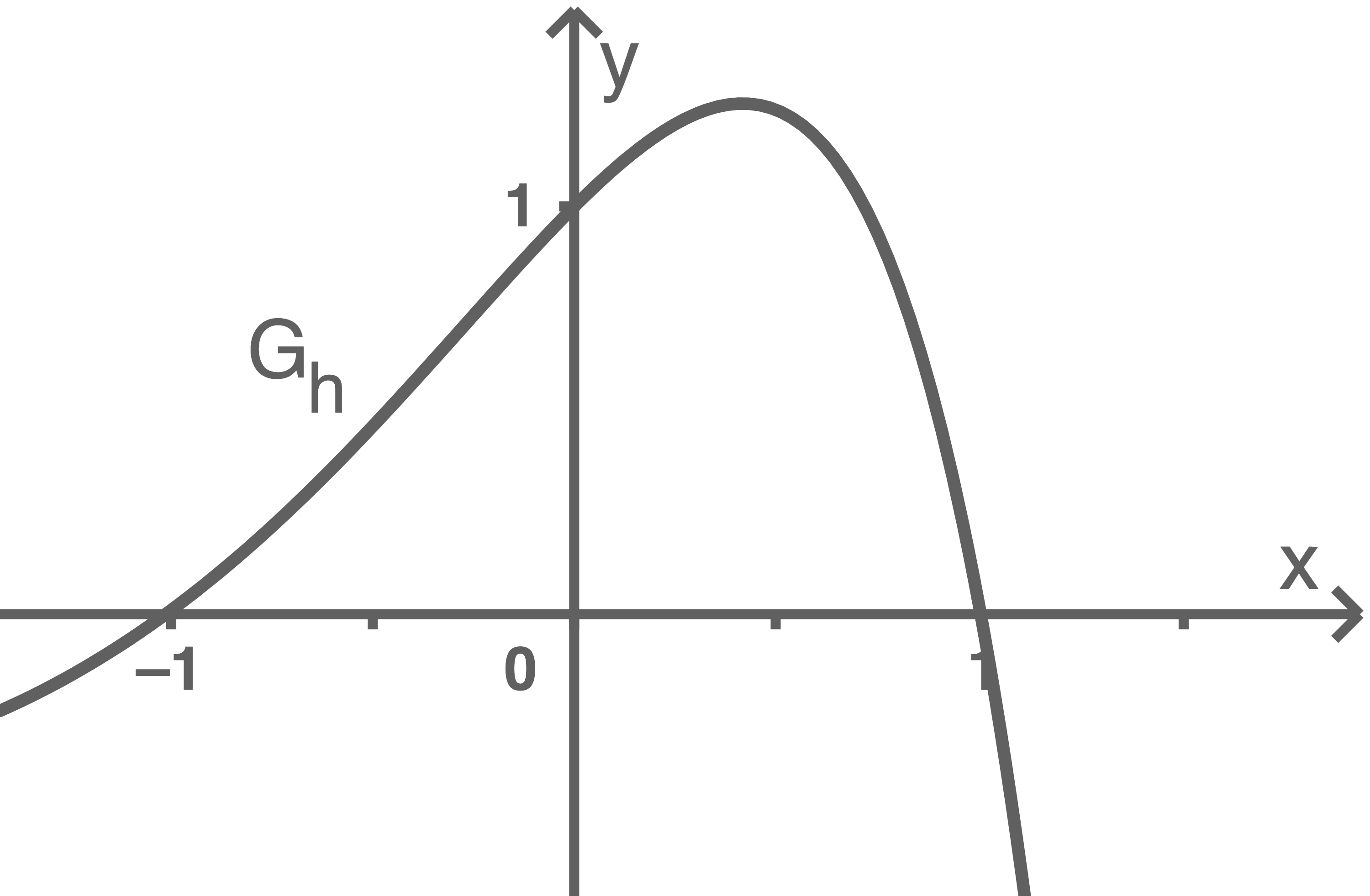
Abbildung 1
c)
Begründe anhand des Funktionsterms von  dass der Funktionswert
dass der Funktionswert  nur für
nur für  positiv ist.
positiv ist.
(3 BE)
d)
Die Gerade  ist die Tangente an
ist die Tangente an  im Punkt
im Punkt  Es gibt genau eine Tangente
Es gibt genau eine Tangente  an
an  , die zu
, die zu  senkrecht ist.
Gib die notwendigen Schritte zur Berechnung einer Gleichung von
senkrecht ist.
Gib die notwendigen Schritte zur Berechnung einer Gleichung von  an und erläutere diese.
an und erläutere diese.
(6 BE)
e)
In einem Wendepunkt von  ist die Steigung von
ist die Steigung von  maximal.
Berechne die Koordinaten dieses Wendepunktes und den Wert der maximalen Steigung.
maximal.
Berechne die Koordinaten dieses Wendepunktes und den Wert der maximalen Steigung.
(5 BE)
f)
Für  wird das Dreieck mit den Eckpunkten
wird das Dreieck mit den Eckpunkten 
 und
und  betrachtet. Für einen Wert von
betrachtet. Für einen Wert von  ist der Flächeninhalt des Dreiecks maximal.
Berechne den maximalen Flächeninhalt.
ist der Flächeninhalt des Dreiecks maximal.
Berechne den maximalen Flächeninhalt.
(5 BE)
g)
(7 BE)

Abbildung 2
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1A
a)
Für die erste Ableitung von  gilt:
gilt:
 Notwendige Bedingung für Extremstellen anwenden:
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/615bcc700b80b81d595528740563be9bb91cbde69f413e591e570b9ab54eae12?color=5a5a5a) Aus der Abbildung lässt sich ablesen, dass der Graph von
Aus der Abbildung lässt sich ablesen, dass der Graph von  für
für  einen Sattelpunkt hat. Da
einen Sattelpunkt hat. Da  eine ganzrationale Funktion vierten Grades ist, besitzt der Graph von
eine ganzrationale Funktion vierten Grades ist, besitzt der Graph von  keine weiteren Extrempunkte.
keine weiteren Extrempunkte.
b)
Gleichung von  ermitteln
Die gesuchte Gerade
ermitteln
Die gesuchte Gerade  besitzt die allgemeine Gleichung
besitzt die allgemeine Gleichung  wobei der
wobei der  -Achsenabschnitt
-Achsenabschnitt  als
als  gegeben ist, da
gegeben ist, da  durch
durch  verläuft.
Einsetzen der Koordinaten von
verläuft.
Einsetzen der Koordinaten von  und Auflösen nach der Steigung
und Auflösen nach der Steigung  liefert:
Eine Gleichung von
liefert:
Eine Gleichung von  ist somit durch
ist somit durch  gegeben.
Tangente rechnerisch nachweisen
Es muss gezeigt werden, dass
gegeben.
Tangente rechnerisch nachweisen
Es muss gezeigt werden, dass  durch den Punkt
durch den Punkt  verläuft und in diesem die Steigung
verläuft und in diesem die Steigung  besitzt.
Es gilt:
besitzt.
Es gilt:

 Einsetzen von
Einsetzen von  in
in  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
f(5)&=&\dfrac{3}{1000} \cdot 5^4-\dfrac{8}{100} \cdot 5^3+\dfrac{6}{10} \cdot 5^2 \\[5pt]
&=& 6,875 \\[5pt]
&=&t(5) \\[10pt]
f](https://mathjax.schullv.de/741649c3400e9d47368d2f2e4bae92b8c3f804a7191cce9e80b1699d8684241a?color=5a5a5a) Somit ist
Somit ist  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt mit den Koordinaten
im Punkt mit den Koordinaten 
c)
Die beiden Flächenstücke werden durch die Schnittstellen der beiden Graphen begrenzt. Diese ergeben sich zu:
![\(\begin{array}[t]{rll}
f(x)&=& t(x)& \quad \scriptsize \mid \; GTR \\[5pt]
x_1&=&\dfrac{25-5 \sqrt{22}}{3} \\[5pt]
x_2&=&5 \\[5pt]
x_3&=&\dfrac{25+5 \sqrt{22}}{3}
\end{array}\)](https://mathjax.schullv.de/c733fa39a545af10cbd3f0af1bdbe18ffeeb147127c0d458dc4447b24f699558?color=5a5a5a) Da
Da  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist, berührt sie diesen an der Stelle
ist, berührt sie diesen an der Stelle  nur.
Der Graph von
nur.
Der Graph von  verläuft im betrachteten Intervall somit vollständig oberhalb des Graphen von
verläuft im betrachteten Intervall somit vollständig oberhalb des Graphen von  Für den Flächeninhalt folgt also mit dem GTR:
Für den Flächeninhalt folgt also mit dem GTR:
![\(\displaystyle\int_{x_1}^{x_3}\left(\dfrac{3}{2} x-\dfrac{5}{8}-f(x)\right)\;\mathrm dx \approx 44,59 \; [\text{FE}]\)](https://mathjax.schullv.de/265f3e4856194c2937b770a90ba3ac664640167ae2a5a8e08f514aa089270606?color=5a5a5a)
d)
Der Graph von  entsteht aus dem Graphen von
entsteht aus dem Graphen von  durch Streckung mit dem Faktor
durch Streckung mit dem Faktor  in
in  -Richtung und mit dem Faktor
-Richtung und mit dem Faktor  in
in  -Richtung.
Für
-Richtung.
Für  ergibt sich durch Einsetzen der gegebenen Koordinaten:
ergibt sich durch Einsetzen der gegebenen Koordinaten:
![\(\begin{array}[t]{rll}
g(12)&=&a\cdot f(10) \\[5pt]
12&=&a\cdot 10 &\quad \scriptsize \mid\;:10\\[5pt]
\dfrac{6}{5}&=&a
\end{array}\)](https://mathjax.schullv.de/fb0e63842b8203e0965a8cc09a7d47dc63d3f9716e310d71204577be3675459f?color=5a5a5a) Für den Wert von
Für den Wert von  gilt:
gilt:
![\(\begin{array}[t]{rll}
12&=&\dfrac{1}{b}\cdot10 &\quad \scriptsize \mid\;\cdot b \\[5pt]
12b&=&10 &\quad \scriptsize \mid\;:12\\[5pt]
b&=&\dfrac{5}{6}
\end{array}\)](https://mathjax.schullv.de/a6407b1ce3258c26bd3aee3b2825928c97313c2e4458c8205aa2996e69b0c5ca?color=5a5a5a)
e)
Geschwindigkeit berechnen
![\(\begin{array}[t]{rll}
f(3)&=&\dfrac{3}{1000} \cdot 3^4-\dfrac{8}{100} \cdot 3^3+\dfrac{6}{10} \cdot 3^2 \\[5pt]
&\approx&3,48
\end{array}\)](https://mathjax.schullv.de/a76ae2a9472aad2b6c5161da19e7b6f2e6ef6dac2ab68013fcd276c1d2b5a226?color=5a5a5a) Drei Sekunden nach dem Start beträgt die Geschwindigkeit von Radfahrer
Drei Sekunden nach dem Start beträgt die Geschwindigkeit von Radfahrer  somit ca.
somit ca.  Zeitpunkt berechnen
Für den Zeitpunkt, zu dem er eine Geschwindigkeit von
Zeitpunkt berechnen
Für den Zeitpunkt, zu dem er eine Geschwindigkeit von  hat, liefert die Gleichung
hat, liefert die Gleichung  mit dem solve-Befehl des GTR folgende Lösung im betrachteten Zeitraum:
mit dem solve-Befehl des GTR folgende Lösung im betrachteten Zeitraum:
 Radfahrer
Radfahrer  erreicht somit ca.
erreicht somit ca.  Sekunden nach dem Start eine Geschwindigkeit von
Sekunden nach dem Start eine Geschwindigkeit von 
f)
Konstante Geschwindigkeit ermitteln
![\(\begin{array}[t]{rll}
h(12)&=&\dfrac{1}{576} \cdot 12^4-\dfrac{1}{18} \cdot 12^3+\dfrac{1}{2} \cdot 12^2 \\[5pt]
&=&12
\end{array}\)](https://mathjax.schullv.de/8e6ceec7d94d3bd869d3b82fa5b7a13b625dea3d54a03b45fc0ee010856879bc?color=5a5a5a) Die gesuchte konstante Geschwindigkeit von Radfahrer
Die gesuchte konstante Geschwindigkeit von Radfahrer  beträgt somit
beträgt somit  Waagrechte Tangente zeigen
Mit dem GTR folgt, dass
Waagrechte Tangente zeigen
Mit dem GTR folgt, dass  gilt. Somit ist die Tangente an den Graphen von
gilt. Somit ist die Tangente an den Graphen von  an dieser Stelle waagrecht.
an dieser Stelle waagrecht.
g)
Aus der Gleichung  folgt mit dem GTR als Lösung im Zeitraum
folgt mit dem GTR als Lösung im Zeitraum 

h)
1. Schritt: Zeitpunkt des Überholens berechnen
Zu dem Zeitpunkt im Intervall  an dem einer der beiden Radfahrer den anderen überholt und die beiden Radfahrer somit die gleiche Strecke zurückgelegt haben, gilt:
an dem einer der beiden Radfahrer den anderen überholt und die beiden Radfahrer somit die gleiche Strecke zurückgelegt haben, gilt:
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{z}(f(x)-h(x))\;\mathrm dx&=& 0 &\quad \scriptsize \mid\; CAS \\[5pt]
z_0&=& \dfrac{1100-20 \sqrt{295}}{91} &\\[5pt]
z_0&\approx & 8,31
\end{array}\)](https://mathjax.schullv.de/cded9ccd46b01c22d8d983c864ce1693ca2351c5d92375f77a0b0845acde1e46?color=5a5a5a) 2. Schritt: Prozentuale Überschreitung berechnen
Zum Zeitpunkt
2. Schritt: Prozentuale Überschreitung berechnen
Zum Zeitpunkt  ist der Radfahrer
ist der Radfahrer  schneller. Für den Wert in Prozent, um den die Geschwindigkeit von Radfahrer
schneller. Für den Wert in Prozent, um den die Geschwindigkeit von Radfahrer  die Geschwindigkeit von Radfahrer
die Geschwindigkeit von Radfahrer  zu diesem Zeitpunkt übersteigt, ergibt sich mit dem CAS:
zu diesem Zeitpunkt übersteigt, ergibt sich mit dem CAS:
![\(\begin{array}[t]{rll}
\dfrac{h\left(z_0\right)-f\left(z_0\right)}{f\left(z_0\right)}& \approx &0,11 & \\[5pt]
&=& 11\,\%
\end{array}\)](https://mathjax.schullv.de/ffbe6f71845a55e8d7bcf52bf898bd05a0b1df433209251ad7fcedb4b045e74c?color=5a5a5a)
Lösung 1B
a)
Wassertemperatur angeben
![\(\begin{array}[t]{rll}
f(0)&=& 25 - 20 \cdot \mathrm{e}^{-0,014\cdot0} \\[5pt]
&=& 25 - 20 \\[5pt]
&=& 5\;[^\circ C]
\end{array}\)](https://mathjax.schullv.de/a95daf75b0ad3c41aa6330cd4c588191ff485584733881291b9ed5d2c1d2afa7?color=5a5a5a) Zeitpunkt bestimmen
Zu dem Zeitpunkt, an dem die Wassertemperatur
Zeitpunkt bestimmen
Zu dem Zeitpunkt, an dem die Wassertemperatur  beträgt, gilt:
beträgt, gilt:
![\(\begin{array}[t]{rll}
f(t)&=& 12 \\[5pt]
25 - 20 \cdot \mathrm{e}^{-0,014t}&=& 12 &\quad \scriptsize \mid\;-25 \\[5pt]
- 20 \cdot \mathrm{e}^{-0,014t}&=& -13 &\quad \scriptsize \mid\;:(-20) \\[5pt]
\mathrm{e}^{-0,014t}&=&\dfrac{13}{20} \\[5pt]
-0,014t&=&\ln\left(\dfrac{13}{20}\right) &\quad \scriptsize \mid\;:(-0,014) \\[5pt]
t&\approx& 30,77
\end{array}\)](https://mathjax.schullv.de/3b20a3509fc8f024ef86534c3814025e9b7e36741bdc2f2c22df1884e3843a5b?color=5a5a5a) Die Wassertemperatur beträgt somit nach etwa
Die Wassertemperatur beträgt somit nach etwa  Minuten
Minuten 
b)
Für die erste Ableitung von  gilt:
gilt:
 Für
Für  gilt also:
gilt also:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/7728a4fbebe0af39d3cf29d7d0aa0351d83ca6f9791e7773b0ff1d80da96ab90?color=5a5a5a) Der Term beschreibt die momentane Änderungsrate der Wassertemperatur 30 Minuten nach Entnahme in Grad pro Minute.
Der Term beschreibt die momentane Änderungsrate der Wassertemperatur 30 Minuten nach Entnahme in Grad pro Minute.
c)
Für alle  gilt
gilt  .
Da nur für Werte
.
Da nur für Werte  der Wert des Terms
der Wert des Terms  positiv ist, ist
positiv ist, ist  nur für diese Werte positiv.
nur für diese Werte positiv.
d)
Die Gerade  hat im Punkt
hat im Punkt  die Steigung
die Steigung  Eine Tangente
Eine Tangente  die senkrecht zur Gerade
die senkrecht zur Gerade  in diesem Punkt verläuft, hat die Steigung
in diesem Punkt verläuft, hat die Steigung  Zur Bestimmung der
Zur Bestimmung der  -Koordinate
-Koordinate  des Berührpunkts
des Berührpunkts  von
von  und
und  wird die Gleichung
wird die Gleichung  gelöst.
Bestimmung der
gelöst.
Bestimmung der  -Koordinate
-Koordinate  von
von 
 Der
Der  -Achsenabschnitt von
-Achsenabschnitt von  wird schließlich durch Einsetzen der der Steigung von
wird schließlich durch Einsetzen der der Steigung von  und der Koordinaten von
und der Koordinaten von  in die allgemeine Tangentengleichung
in die allgemeine Tangentengleichung  berechnet.
berechnet.
e)
Wendestellen bestimmen
Zweite Ableitung bestimmen:
Notwendige Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/40ed5e3c72c3aacc5413344ba8c5a9ab43b0d869bdc406eb2d479032e1c9c2ff?color=5a5a5a) Mit dem GTR folgt:
Mit dem GTR folgt:

 Hinreichende Bedingung für Wendestellen anwenden:
Hinreichende Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/ddc3ac7be9fcdb8a08142253bcb7b51c6d54eac8b5c94316e00577b990f6b582?color=5a5a5a) Die Wendestellen von
Die Wendestellen von  sind somit gegeben durch
sind somit gegeben durch  und
und 
 -Koordinaten berechnen:
-Koordinaten berechnen:
![\(\begin{array}[t]{rll}
h(-2-\sqrt{3})&\approx& -0,31 & \\[5pt]
h(-2+\sqrt{3})&\approx& 0,71 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ede2e0c849ae032ab189f38bdd7a433754a139004384844cea8da2d424606051?color=5a5a5a) Die Koordinaten der Wendepunkte folgen also mit
Die Koordinaten der Wendepunkte folgen also mit  und
und  Wert der maximalen Steigung berechnen
Steigung in den Wendepunkten berechnen:
Wert der maximalen Steigung berechnen
Steigung in den Wendepunkten berechnen:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/b45056367a91e4dd8b6b7b732c032e55329906845707b8b9a4f04e2927e971c5?color=5a5a5a) Wegen
Wegen  hat
hat  an der Stelle
an der Stelle  ein Maximum.
Der gesuchte Wendepunkt hat also die Koordinaten
ein Maximum.
Der gesuchte Wendepunkt hat also die Koordinaten  Der Wert der maximalen Steigung ist dann:
Der Wert der maximalen Steigung ist dann:

f)
Der Flächeninhalt des Dreiecks in Abhängigkeit von  lässt sich wie folgt berechnen:
lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
a(w)&=& \dfrac{1}{2}\cdot w\cdot h(w) \\[5pt]
&=& \dfrac{1}{2}\cdot w\cdot (1-w^2) \cdot \mathrm{e}^w \\[5pt]
&=& \dfrac{1}{2}\cdot w\cdot \mathrm{e}^w- \dfrac{1}{2}\cdot w^3\cdot \mathrm{e}^w
\end{array}\)](https://mathjax.schullv.de/a055970e253399f4e0b4f961296b8f3ede7269928eccbc33b94f358756f68fd7?color=5a5a5a) Für die Ableitung gilt:
Um den maximalen Flächeninhalt zu berechnen, wird die notwendige Bedingung für Extremstellen angewendet:
Für die Ableitung gilt:
Um den maximalen Flächeninhalt zu berechnen, wird die notwendige Bedingung für Extremstellen angewendet:
![\(\begin{array}[t]{rll}
a](https://mathjax.schullv.de/340b8e149a37264fa9c286800864cf48f48994ee068872f5d7fa697815deca9e?color=5a5a5a) Mit dem GTR folgt
Mit dem GTR folgt  Wegen
Wegen  beträgt der maximale Flächeninhalt ungefähr
beträgt der maximale Flächeninhalt ungefähr 
g)
Für die  -Koordinate
-Koordinate  von
von  gilt:
gilt: