Aufgabe 3A

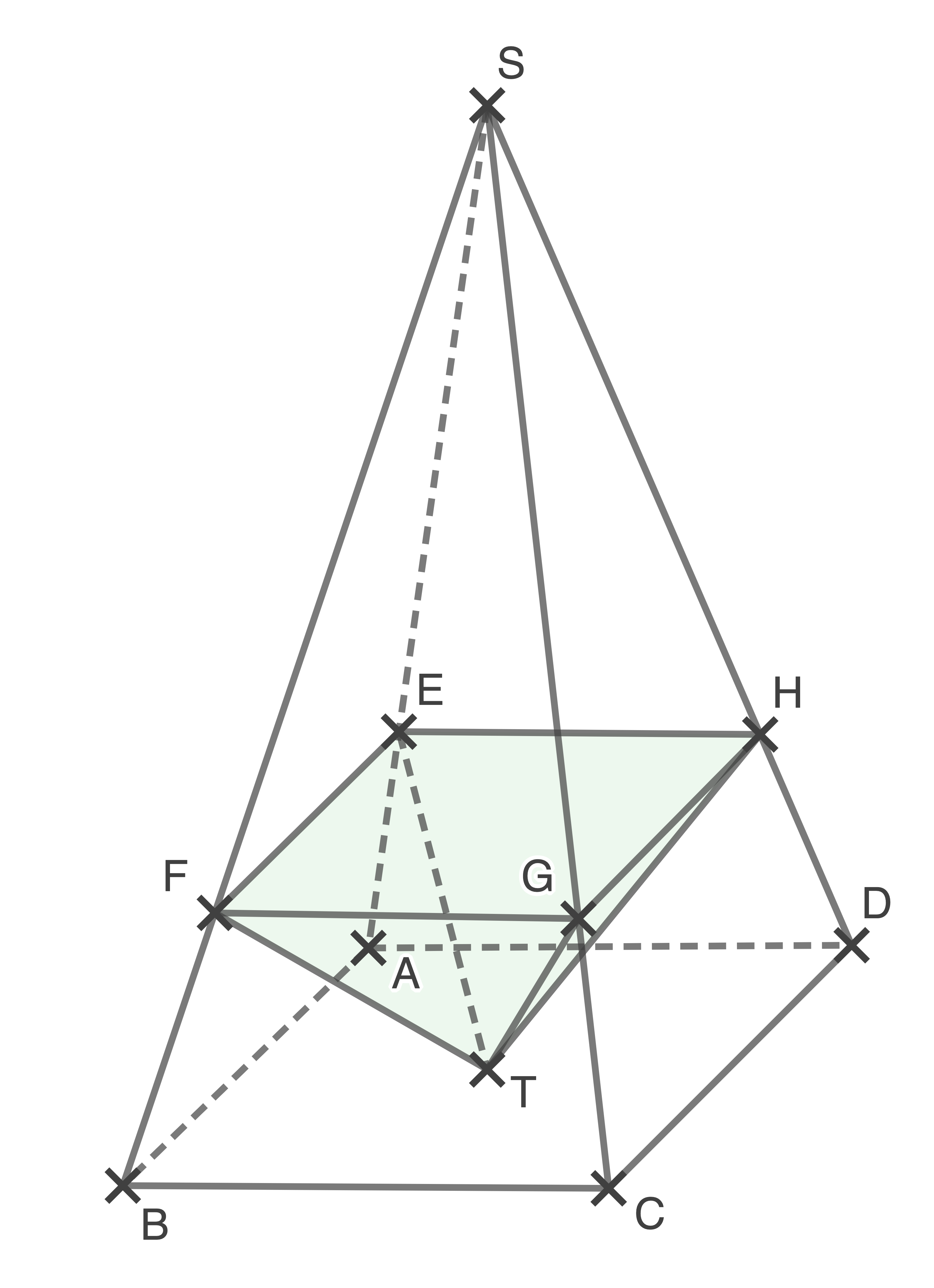
Die Abbildung zeigt die Pyramide $ABCDS$ mit $A(0 \mid 0 \mid 0), B(2 \mid 0 \mid 0), C(2 \mid 2 \mid 0),$ $D(0 \mid 2 \mid 0)$ und $S(1 \mid 1 \mid 4)$ .

Die Grundfläche $ABCD$ ist quadratisch.
Der Schnittpunkt der Diagonalen der Grundfläche $ABCD$ wird mit $T$ bezeichnet.

3D-Diagramm eines geometrischen Körpers mit verschiedenen Punkten und Linien.

Gib die Koordinaten des Punktes $T$ an.
Berechne den Inhalt der Oberfläche der Pyramide $ABCDS$ .

(6 BE)

Bestimme die Größe des Winkels zwischen den Kanten $\overline{AS}$ und $\overline{AB}$ .

(3 BE)

Der Mittelpunkt der Kante $\overline{CD}$ wird mit $M$ bezeichnet.
Untersuche, ob es einen Punkt $P$ auf der Kante $\overline{DS}$ gibt, für den das Dreieck $BMP$ im Punkt $M$ rechtwinklig ist.

(5 BE)

Die vier Punkte $E, F, G$ und $H$ liegen jeweils auf einer der vier vom Punkt $S$ ausgehenden Kanten und haben alle die $z$ -Koordinate 1 (vgl. Abbildung).

Gegeben ist die folgende Lösung einer Aufgabe im Zusammenhang mit den betrachteten geometrischen Objekten:

$\pmatrix{2\\0\\0}+k \cdot \pmatrix{-1\\1\\4} = \pmatrix{x\\y\\1}$

liefert $k = \frac{1}{4}$ und damit $x= 1,75$ und $y=0,25.$

Gib eine passende Aufgabenstellung an und erläutere den Ansatz der gegebenen Lösung.

(3 BE)

Ermittle das Volumen der Pyramide $EFGHT$ .

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\overrightarrow{OT}=\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}$ $=\pmatrix{1\\1\\0}$
Die Koordinaten des Punktes $T$ sind gegeben durch $T(1 \mid 1 \mid 0).$

$\overrightarrow{AB}= \pmatrix{2\\0\\0}$ , $\mid \overrightarrow{AB} \mid = 2\,[\text{LE}]$
Da die Grundfläche der Pyramide quadratisch ist, kann der Flächeninhalt der Grundfläche berechnet werden durch $\mid \overrightarrow{AB} \mid^2 =2^2 =4\,[\text{FE}].$
Die Koordinaten des Mittelpunkts der Strecke $\overline{AB}$ sind gegeben durch $Z(1 \mid 0 \mid 0).$ Es gilt also $\overrightarrow{ZS}=\pmatrix{0\\1\\4}$ und damit insbesondere $\mid \overrightarrow{ZS} \mid=\sqrt{0^2+1^2+4^2}=\sqrt{17}$ $\approx 4,12\,[\text{LE}].$
Der Flächeninhalt der Oberfläche der Pyramide ist gegeben durch die Summe des Flächeninhalts der Grundfläche und der vier Seitenflächen:
$4 +4 \cdot \dfrac{1}{2} \cdot 2 \cdot \sqrt{17} \approx 20,5\,[\text{FE}]$
Der Inhalt der Oberfläche der Pyramide ist gegeben durch $20,5\,\text{FE}.$

$\overrightarrow{AB}=\pmatrix{2\\0\\0}, \mid \overrightarrow{AB} \mid = 2$

$\overrightarrow{AS} = \pmatrix{1\\1\\4}, \mid \overrightarrow{AS} \mid = \sqrt{18}$

Berechnung des Winkels mit der Formel für Winkel zwischen zwei Vektoren:

$\dfrac{\overrightarrow{AB} \circ \overrightarrow{AS}}{\mid \overrightarrow{AB}\mid \cdot \mid \overrightarrow{AS} \mid}$ $= \dfrac{2 \cdot 1 + 0 \cdot 1 + 0 \cdot 4}{2 \cdot \sqrt{18}}\approx 0,24$

$\begin{array}[t]{rll} \cos(\alpha)&=& 0,24&\quad \scriptsize \mid\;\cos^{-1} \\[5pt] \alpha &\approx& 76,11 \end{array}$

Der gesuchte Winkel hat ungefähr $76,11^{\circ}.$

$\overrightarrow{OM}=\overrightarrow{OC}+\dfrac{1}{2}\overrightarrow{CD}=\pmatrix{1\\2\\0}$
Die Koordinaten des Mittelpunkts der Kante $\overline{CD}$ sind gegeben durch $M (1 \mid 2 \mid 0).$

Die Gerade durch die Punkte $D$ und $S$ ist gegeben durch $g: \overrightarrow{x}= \overrightarrow{OD}+ r \cdot \overrightarrow{DS}$ $= \pmatrix{0\\2\\0}+ r\cdot \pmatrix{1\\-1\\4}.$

Die Punkte auf $g$ haben also die Koordinaten $P(r \mid 2-r \mid 4r).$ Für $r \in [0,1]$ liegt ein Punkt $P$ auf der Kante zwischen $D$ und $S.$
Damit das Dreieck $BMP$ im Punkt $M$ einen rechten Winkel hat, muss $\overrightarrow{MB} \circ \overrightarrow{MP}=0$ gelten.

$\overrightarrow{MB}= \overrightarrow{OB}-\overrightarrow{OM} = \pmatrix{1\\-2\\0},$ $\overrightarrow{MP}=\overrightarrow{OP}-\overrightarrow{OM}=\pmatrix{r-1\\-r\\4r}$

$\overrightarrow{MB} \circ \overrightarrow{MP}=\pmatrix{1\\-2\\0} \circ \pmatrix{r-1\\-r\\4r}$ $=1 \cdot (r-1) +(-2)\cdot(-r)+0\cdot 4r$ $=3r-1$

Für $r=\dfrac{1}{3}$ gilt $\overrightarrow{MB} \circ \overrightarrow{MP}=0.$ Ein solcher Punkt $P$ existiert also.

Eine passende Aufgabe zur gegebenen Lösung ist: "Bestimme die $x$ - und $y$ -Koordinaten des Punktes $F$ ".
Der Ansatz ermitelt die $x$ - und $y$ -Koordinate von $F$ wie folgt: Die Gleichung der Geraden durch die Punkte $B$ und $S$ wird gleichgesetzt mit den Koordinaten des Punktes $F$ , von dem nur die $z$ -Koordiate bekannt ist. Dadurch lässt sich der Faktor $k$ ermitteln, mit dem dann wiederum die $x$ - und $y$ -Koordinate berechnet werden können.

Mit Aufgabenteil d) ist bekannt, dass dass $F=(1,75 \mid 0,25 \mid 1)$ und analog $G=(1,75 \mid 1,75 \mid 1)$ gilt. Daraus folgt $\overrightarrow{FG}=\pmatrix{0\\1,5\\0}$ und damit $\mid \overrightarrow{FG} \mid = 1,5\,[\text{LE}].$
Die Grundfläche der Pyramide ist quadratisch und die Höhe ist durch die $z$ -Koordinate der Punkte auf der Grundfläche gegeben, also $h=1\,[\text{LE}].$
Das Volumen der Pyramide lässt sich damit insgesamt wie folgt berechnen:
$\dfrac{1}{3} \cdot 1,5^2 \cdot 1 = 0,75\,[\text{VE}]$

Das Volumen der Pyramide ist gegeben durch $0,75\,\text{VE}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?