Aufgabe 3B
Betrachtet wird der Stumpf  der schiefen Pyramide
der schiefen Pyramide  Die Grundfläche
Die Grundfläche  mit
mit 

 und
und  sowie die Deckfläche des Stumpfs mit
sowie die Deckfläche des Stumpfs mit 

 und
und  sind quadratisch.
sind quadratisch.
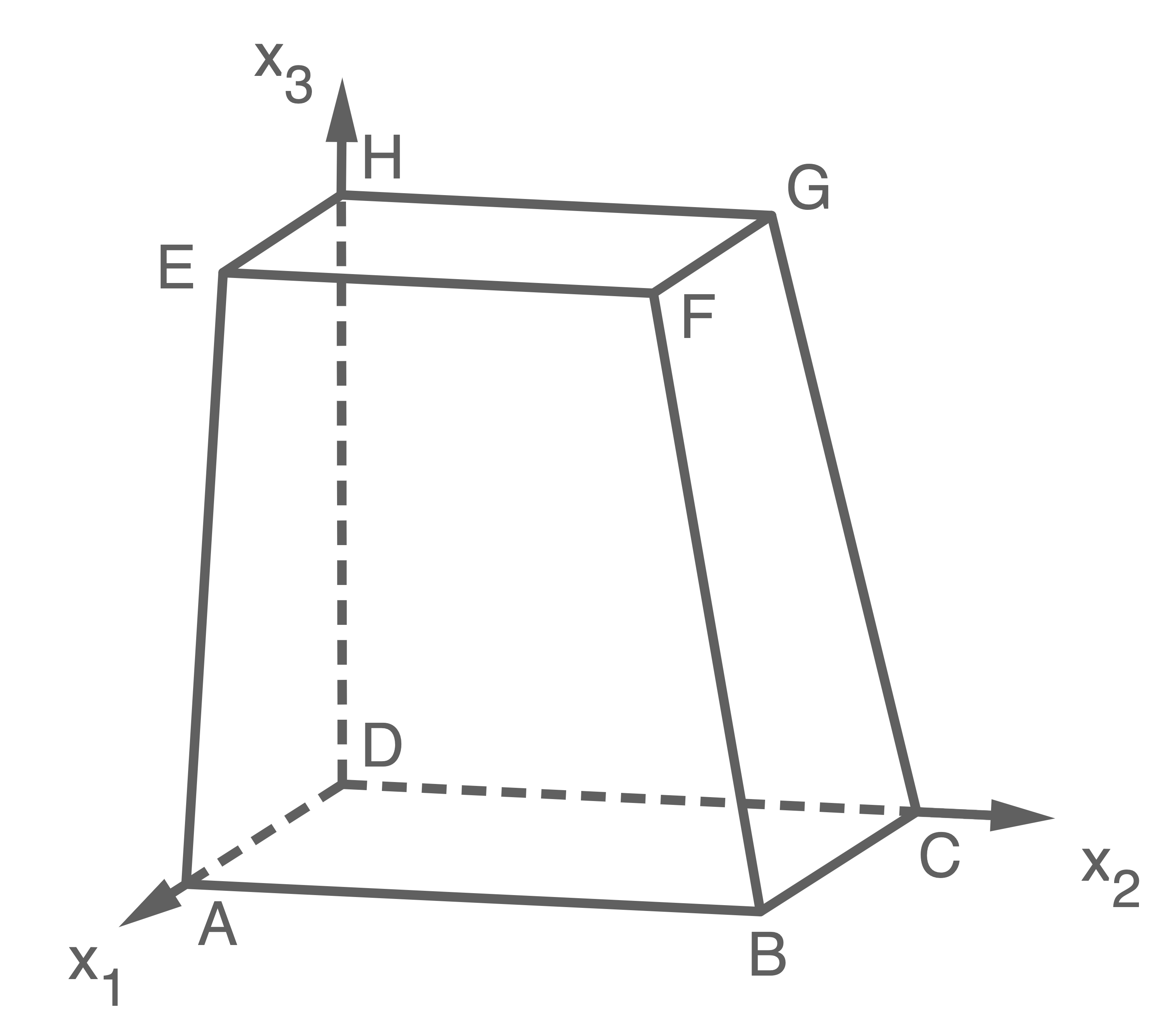
a)
Berechne
- die Länge der Strecke
- die Koordinaten des Mittelpunktes der Strecke
.
(3 BE)
b)
Erläutere den folgenden Ansatz zur Berechnung der Koordinaten der Pyramidenspitze 

(3 BE)
c)
Bestimme das Volumen des Stumpfs.
(3 BE)
d)
Der Pyramidenstumpf wird soweit um die Kante  gedreht bis die Fläche
gedreht bis die Fläche  in der
in der  -Ebene liegt.
-Ebene liegt.
Gib die Koordinaten eines Bildpunktes an.
an.
Der Mittelpunkt Gib die Koordinaten eines Bildpunktes
(2 BE)
e)
Für einen Punkt  der Kante
der Kante  schneidet die Gerade durch
schneidet die Gerade durch  und
und  die Gerade
die Gerade 
Berechne den zugehörigen Wert von
Berechne den zugehörigen Wert von
(4 BE)
f)
Es gibt Punkte  der Kante
der Kante  , für die der von den Strecken
, für die der von den Strecken  und
und  eingeschlossene Winkel größer als
eingeschlossene Winkel größer als  ist.
ist.
Ermittle die zugehörigen Werte von .
.
Ermittle die zugehörigen Werte von
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Es ist: ![\(|\overrightarrow{D F}|=\left|\left(\begin{array}{l}3 \\ 3 \\ 4\end{array}\right) \right| \approx 5,83 \; [\text{LE}]\)](https://mathjax.schullv.de/9d7bbbddcbf1f872d06014af1ec42179b3ef75f5b230d92a1820370d13081850?color=5a5a5a) Die Koordinaten des Mittelpunktes der Strecke
Die Koordinaten des Mittelpunktes der Strecke  folgen mit:
folgen mit:


b)
c)
Das Volumen des Stupfes berechnet sich aus dem Gesamtvolumen der Pyramide minus dem Volumen der Pyramide die sich von der Oberseite des Stumpf bis zur Spitze hin erstreckt.
Volumen: 
![\(=\dfrac{148}{3} \; [\text{VE}]\)](https://mathjax.schullv.de/dfe0dc5c70c40b34d3183cac6b6d15db1d9788b744d02a4098592dbee4fca203?color=5a5a5a)
d)
Mögliche Koordinaten sind beispielsweise  oder als zweite mögliche Lösung
oder als zweite mögliche Lösung 
e)
f)