Aufgabe 1A
Aufgabe 1A
In einem Betrieb wird im Produktionsprozess ein Gas verbraucht. Dazu wird das benötigte Gas durch eine Leitung aus dem Gastank in die Produktionsstätte geleitet. Das hierbei pro Zeit durch die Leitung strömende Gas wird als Gasstrom bezeichnet. Dieser wird in Litern pro Stunde| Zeit in |
||||
|---|---|---|---|---|
| Gasstrom in |
a)
Der Betriebsleiter stimmt der Nutzung des Modells unter folgenden Bedingungen zu:
 die Bedingungen des Betriebsleiters erfüllt werden und
die Bedingungen des Betriebsleiters erfüllt werden und  somit für die folgenden Berechnungen genutzt werden kann.
Bestimme den Zeitpunkt zwischen den Zeitpunkten der Spitzenwerte im Gasstrom, an dem der Gasstrom am stärksten abnimmt.
Berechne die Gesamtzeit im Laufe eines Arbeitstages, in welcher der Gasstrom mindestens
somit für die folgenden Berechnungen genutzt werden kann.
Bestimme den Zeitpunkt zwischen den Zeitpunkten der Spitzenwerte im Gasstrom, an dem der Gasstrom am stärksten abnimmt.
Berechne die Gesamtzeit im Laufe eines Arbeitstages, in welcher der Gasstrom mindestens 
 beträgt.
beträgt.
- Die mit dem Modell berechneten Werte weichen nicht mehr als
von den Tabellenwerten ab.
- Die Zeitpunkte der mit dem Modell berechneten Spitzenwerte weichen nicht mehr als
Minuten von den Zeitpunkten der Spitzenwerte der Messung ab.
(13P)
b)
Das Gas wird für den Verbrauch in einem Tank gespeichert. Dem Tank können 
 Gas entnommen werden. Über eine Anzeige wird das noch entnehmbare Gasvolumen in Prozent angezeigt. Zu Beginn eines Arbeitstages ist der Tank vollständig gefüllt, die Anzeige zeigt
Gas entnommen werden. Über eine Anzeige wird das noch entnehmbare Gasvolumen in Prozent angezeigt. Zu Beginn eines Arbeitstages ist der Tank vollständig gefüllt, die Anzeige zeigt  an.
Bestimme das in der ersten Stunde des Arbeitstages entnommene Gasvolumen.
Begründe, dass das für die Produktion zu einem Zeitpunkt
an.
Bestimme das in der ersten Stunde des Arbeitstages entnommene Gasvolumen.
Begründe, dass das für die Produktion zu einem Zeitpunkt  nach Arbeitsbeginn noch entnehmbare Gasvolumen durch die Funktion
nach Arbeitsbeginn noch entnehmbare Gasvolumen durch die Funktion  mit
mit  ,
,  in
in  ,
,  in
in  , beschrieben werden kann.
Der Tank muss aufgefüllt werden, sobald die Anzeige
, beschrieben werden kann.
Der Tank muss aufgefüllt werden, sobald die Anzeige  anzeigt.
Bestimme den Zeitpunkt des Beginns dieses Auftankvorgangs.
anzeigt.
Bestimme den Zeitpunkt des Beginns dieses Auftankvorgangs.
(10P)
c)
Unabhängig vom Sachzusammenhang ist die Funktionenschar  mit
mit
 ,
,  ,
,  , gegeben.
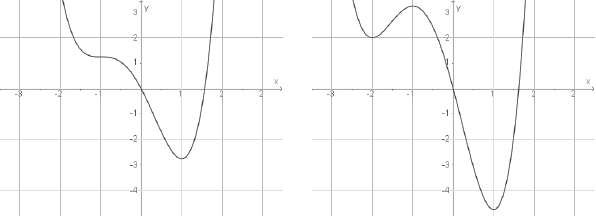
In der Abbildung sind zwei Graphen für
, gegeben.
In der Abbildung sind zwei Graphen für  und
und  dargestellt.
Entscheide, welcher der beiden Graphen zu dem Parameterwert
dargestellt.
Entscheide, welcher der beiden Graphen zu dem Parameterwert  gehört.
Entscheide, ob es einen Wert für
gehört.
Entscheide, ob es einen Wert für  gibt, sodass der Graph von
gibt, sodass der Graph von  symmetrisch zur
symmetrisch zur  -Achse ist.
Es gilt:
-Achse ist.
Es gilt:  .
Begründe damit, dass die Graphen von
.
Begründe damit, dass die Graphen von  entweder drei Extrempunkte oder nur einen Extrempunkt und einen Wendepunkt haben.
entweder drei Extrempunkte oder nur einen Extrempunkt und einen Wendepunkt haben.
Bildnachweise [nach oben]
(11P)
© 2016 - SchulLV.
Aufgabe 1A
a)
- Die mit dem Modell berechneten Werte weichen nicht mehr als
von den Tabellenwerten ab.
- Die Zeitpunkte der mit dem Modell berechneten Spitzenwerte weichen nicht mehr als
Minuten von den Zeitpunkten der Spitzenwerte der Messung ab.
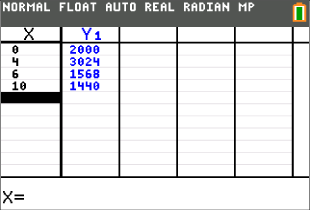 Abb. 1: Tabellenwerte mit dem Taschenrechner bestimmen
Abb. 1: Tabellenwerte mit dem Taschenrechner bestimmen
| Zeit in |
Gas- strom in |
Funktions- werte |
|---|---|---|
Lass dir dazu den Graphen anzeigen. Den Befehl für die Bestimmung von Hochpunkten findest du unter:
 ,
, 
2ND  TRACE (CALC)
TRACE (CALC)  4: maximum
4: maximum
Du erhältst folgende Koordinaten:
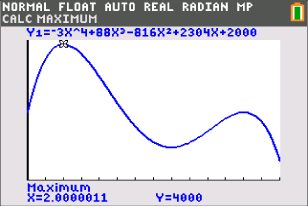 Abb. 2: Hochpunkte mit dem Taschenrechner bestimmen
Abb. 2: Hochpunkte mit dem Taschenrechner bestimmen
Lass dir dazu den Graphen anzeigen. Den Befehl für die Bestimmung von Tiefpunkt findest du unter:

2ND  TRACE (CALC)
TRACE (CALC)  4: minimum
4: minimum
Du erhältst folgende Koordinaten:
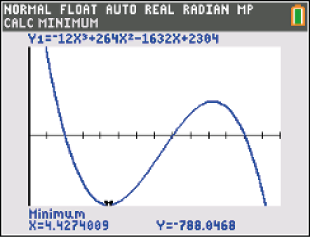 Abb. 3: Tiefpunkt mit dem Taschenrechner bestimmen
Abb. 3: Tiefpunkt mit dem Taschenrechner bestimmen
2ND  TRACE(CLAC)
TRACE(CLAC)  5:intersect
5:intersect
Damit erhälst du das folgende Ergebnis:
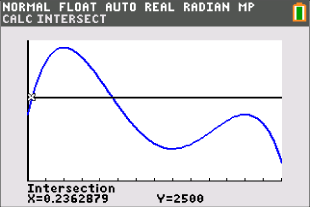 Abb. 4: Schnittpunkte mit dem Taschenrechner bestimmen
Abb. 4: Schnittpunkte mit dem Taschenrechner bestimmen
b)
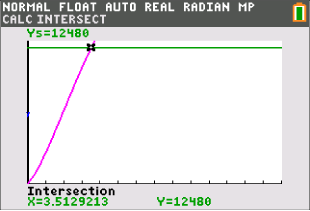 Abb. 5: Schnittpunkt bestimmen
Abb. 5: Schnittpunkt bestimmen
c)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabe 1A
a)
- Die mit dem Modell berechneten Werte weichen nicht mehr als
von den Tabellenwerten ab.
- Die Zeitpunkte der mit dem Modell berechneten Spitzenwerte weichen nicht mehr als
Minuten von den Zeitpunkten der Spitzenwerte der Messung ab.
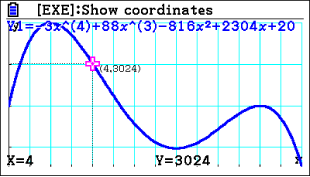 Abb. 1: Tabellenwerte mit dem Taschenrechner bestimmen
Abb. 1: Tabellenwerte mit dem Taschenrechner bestimmen
| Zeit in |
Gas- strom in |
Funktions- werte |
|---|---|---|
Lass dir dazu den Graphen anzeigen. Den Befehl für die Bestimmung von Hochpunkten findest du unter:
 ,
, 
SHIFT  F5
F5  F2
F2
Du erhältst folgende Koordinaten:
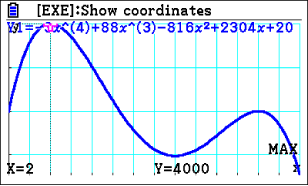 Abb. 2: Hochpunkte mit dem Taschenrechner bestimmen
Abb. 2: Hochpunkte mit dem Taschenrechner bestimmen
Lass dir dazu den Graphen anzeigen. Den Befehl für die Bestimmung von Tiefpunkt findest du unter:

SHIFT  F5
F5  F3
F3
Du erhältst folgende Koordinaten:
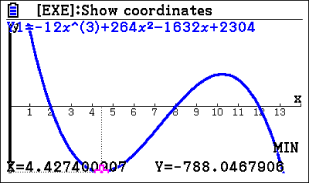 Abb. 3: Tiefpunkt mit dem Taschenrechner bestimmen
Abb. 3: Tiefpunkt mit dem Taschenrechner bestimmen
SHIFT  F5
F5  F5
F5
Damit erhälst du das folgende Ergebnis:
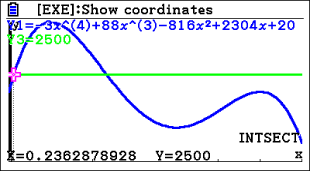 Abb. 4: Schnittpunkte mit dem Taschenrechner bestimmen
Abb. 4: Schnittpunkte mit dem Taschenrechner bestimmen
b)
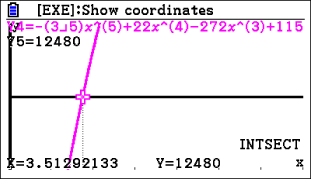 Abb. 5: Schnittpunkt bestimmen
Abb. 5: Schnittpunkt bestimmen
c)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.