Pflichtaufgaben
Aufgabe P1
Gegeben ist die in
a)
Begründe, dass der Graph von 
symmetrisch bezüglich des Koordinatenursprungs ist.
(1 BE)
b)
Der Graph von und die 
-Achse schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
(4 BE)
Aufgabe P2
Bei einer Werbeaktion erhält jedes Kind einen blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball rot ist, beträgt
a)
Zeige, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen roten Ball erhält, kleiner als 
ist.
(2 BE)
b)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term 
berechnet werden kann.
Gib dieses Ereignis an.
(3 BE)
Aufgabe P3
Die Punkte 
, 
, 
und 
sind Eckpunkte des in der Abbildung dargestellten Quaders 
.
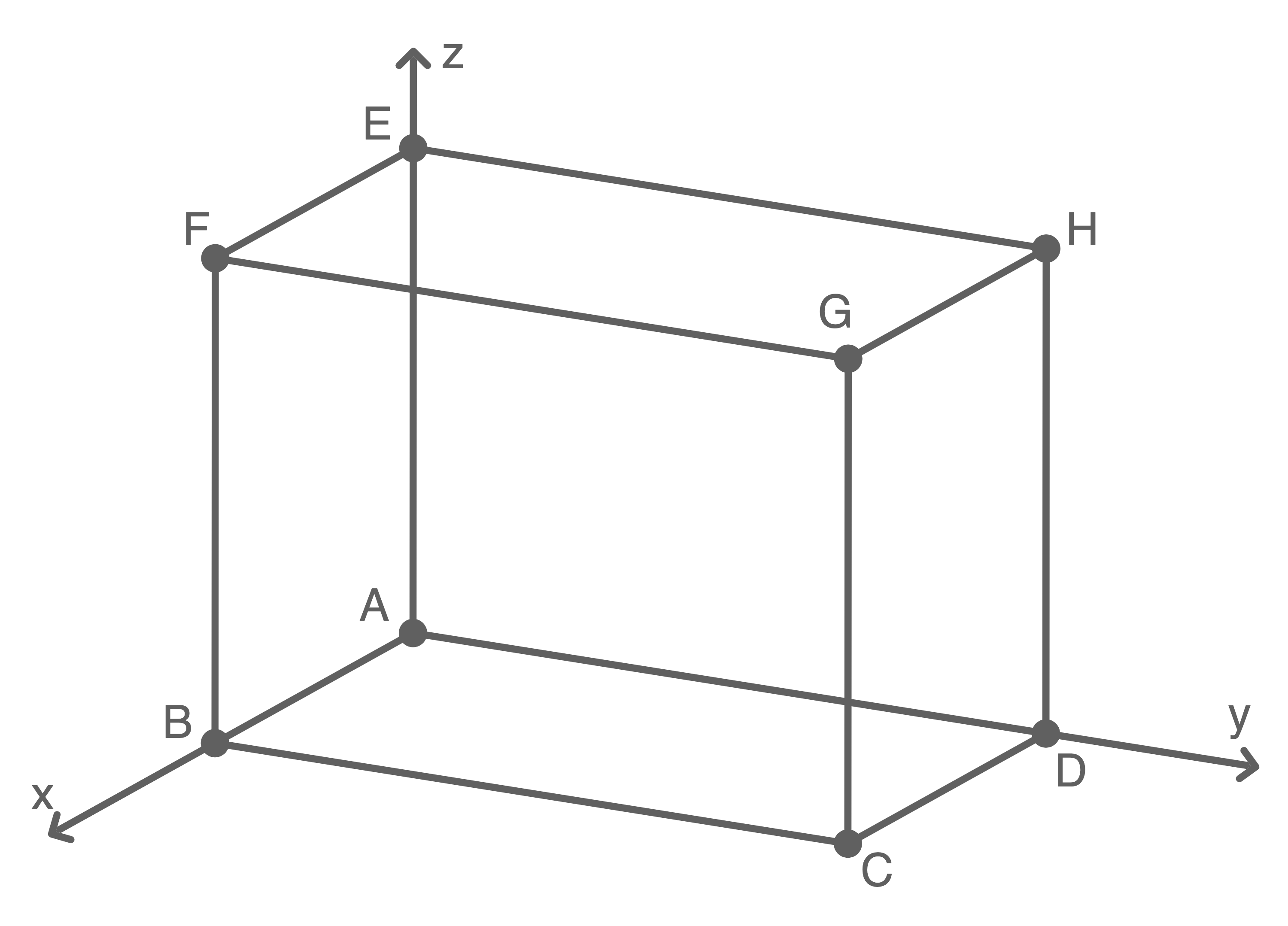
a)
Gib die Koordinaten des Punktes 
an.
Der Quader wird so verschoben, dass sich der Schnittpunkt seiner Raumdiagonalen im Koordinatenursprung befindet. Dabei entsteht der Quader
(1 BE)
b)
Ermittle die Koordinaten des Punkts 
.
(3 BE)
c)
Gib einen Eckpunkt des Quaders 
an, der nur positive Koordinaten hat.
(1 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung P1
a)
Das Polynom 
enthält ausschließlich Potenzen von 
mit ungeraden Exponenten.
b)
Nullstellen berechnen:
![\(\begin{array}[t]{rll}
f(x) &=& 0& \\[5pt]
x^3 - 4x &=& 0& \\[5pt]
x\cdot (x^2-4) &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/daccbd3fff4c407935a8a7e57f107fa259c4bc5632b58ae52118f9148ea2e884?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt direkt 
Die weiteren Nullstellen ergeben sich zu:
![\(\begin{array}[t]{rll}
x^2-4&=& 0&\quad \scriptsize \mid\; +4\\[5pt]
x^2&=& 4&\quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_{2;3 }&=& \pm 2
\end{array}\)](https://mathjax.schullv.de/c69beaa53cdda62fa6fc0cc3fd3d5f0ea4912666d01d0f5c23986be773fafdc2?color=5a5a5a)
Da der Graph von 
symmetrisch zum Ursprung ist, folgt:
Der Inhalt der eingeschlossenen Fläche entspricht somit 8 Flächeneinheiten.
Aufgabe P2
a)
b)
Ein mögliches Zufallsexperiment wäre, dass vier Kinder jeweils einen Ball bekommen.
Ein Ereignis, dessen Wahrscheinlichkeit durch den Term beschrieben wird, ist, dass höchstens einer der Bälle rot ist.
Aufgabe P3
a)
b)
Die Raumdiagonalen des Quaders 
schneiden sich genau in der Mitte des Quaders.
Eine Raumdiagonale des Quaders wird beispielsweise durch die Strecke 
dargestellt. Für den Mittelpunkt dieser Strecke gilt 
und somit 
Für 
gilt also:
Die Koordinaten des Punkts sind somit gegeben durch 
c)