Pflichtteil
Aufgabe P1
Gegeben ist die Funktion
a)
Berechne die Nullstellen der Funktion  .
.
(2P)
b)
Berechne  .
.
(3P)
Aufgabe P2
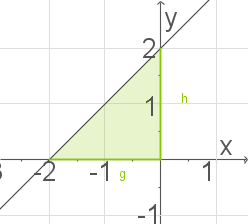
Für jeden Wert vonDie Tangente an den Graphen von
a)
Weise nach, dass für jeden Wert von  die Tangente
die Tangente  durch die Gleichung
durch die Gleichung  beschrieben werden kann.
beschrieben werden kann.
(3P)
b)
Für jeden Wert von  schließen die Tangente
schließen die Tangente  und die beiden Koordinatenachsen ein Dreieck ein.
und die beiden Koordinatenachsen ein Dreieck ein.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von .
.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von
(2P)
Aufgabe P3
Ein Basketballspieler wirftDie Anzahl seiner Treffer wird mit
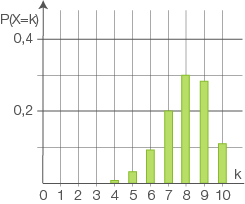
In der Abbildung
a)
Gib mithilfe der Abbildung  einen Näherungswert für die Wahrscheinlichkeit für genau
einen Näherungswert für die Wahrscheinlichkeit für genau  Treffer an.
Treffer an.
Ermittle mithilfe der Abbildung einen Näherungswert für die Wahrscheinlichkeit für mindestens
einen Näherungswert für die Wahrscheinlichkeit für mindestens  Treffer.
Treffer.
Ermittle mithilfe der Abbildung
(3P)
b)
Die Zufallsgröße  ist binomialverteilt mit
ist binomialverteilt mit  und
und  .
.
Stelle in Abbildung die Wahrscheinlichkeitsverteilung von
die Wahrscheinlichkeitsverteilung von  mithilfe der Wahrscheinlichkeitsverteilung von
mithilfe der Wahrscheinlichkeitsverteilung von  dar.
dar.
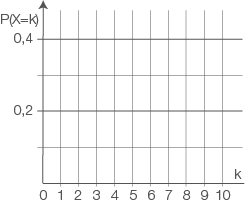 Abb. 2: Koordinatensystem zu Aufgabenteil b)
Abb. 2: Koordinatensystem zu Aufgabenteil b)
Stelle in Abbildung
(2P)
 Abb. 2: Koordinatensystem zu Aufgabenteil b)
Abb. 2: Koordinatensystem zu Aufgabenteil b)
Aufgabe P4
Die unten angegebene Tabelle stellt die Übergänge eines Systems mit zwei ZuständenDie zugehörige Übergangsmatrix wird mit
nach
a)
Stelle den zugehörigen Übergangsgraphen dar.
Berechne die in fehlenden Werte:
fehlenden Werte:  .
.
Berechne die in
(3P)
b)
In einem anderen System mit zwei Zuständen werden die Übergänge durch die Matrix
 beschrieben. Die Anfangsverteilung ist
beschrieben. Die Anfangsverteilung ist  .
.
Zeige, dass sich die Verteilung nach einem Übergang nicht mehr ändert.
Bildnachweise [nach oben]
Zeige, dass sich die Verteilung nach einem Übergang nicht mehr ändert.
(2P)
© 2016 - SchulLV.
Aufgabe P1
a)
b)
- Integrieren des Funktionsterms
- Einsetzen der Grenzen
Aufgabe P2
a)
b)
Die Höhe entspricht dem in der Tangentengleichung gegebenen
Der Flächeninhalt des Dreiecks ist somit:
Aufgabe P3
a)
Somit ist
b)
- In Summe sind alle Balken gleich 1
- Der Balken bei
muss der größte sein
- Die Höhe der Balken berechnest du über eine Binominalverteilung
Tipp: Es ist zu erwarten, dass die Wahrscheinlichkeit ab einem Wert für
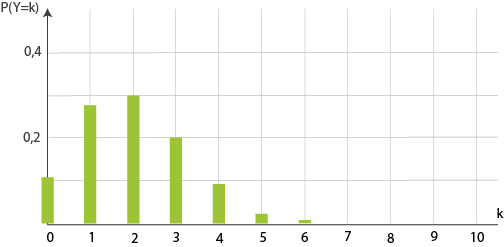 Abb. 2: Wahrscheinlichkeitsverteilung
Abb. 2: Wahrscheinlichkeitsverteilung
Aufgabe P4
a)
Jeder Zustand wird mit einem Kreis dargestellt. Von jedem Zustand zu jedem Zustand verläuft ein Pfeil, an dem die Übergangswahrscheinlichkeit steht. Dabei gilt, dass die Summe der von einem Zustand ausgehenden Übergangswahrscheinlichkeiten immer gleich 1 ist.
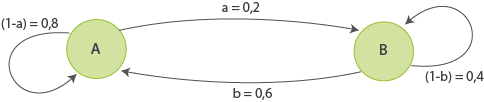 Abb. 3: Übergangsgarph für die Zustände A und B
Abb. 3: Übergangsgarph für die Zustände A und B
Dies ist auf zwei Arten möglich:
- Von A nach A und danach von A nach A
- Von A nach B und danach von B nach A
Dies ist auch auf zwei Arten möglich:
- Von B nach A und danach von A nach A
- Von B nach B und danach von B nach A
b)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.