Aufgabe 3A

Eine Pyramide mit viereckiger Grundfläche hat die Eckpunkte $A(-3\mid 0\mid 0)$ , $B(3\mid 0\mid 0)$ , $C(1,5\mid 2\mid 0)$ , $D(-1,5\mid 2\mid 0)$ und $S(0\mid 2\mid 2)$ .

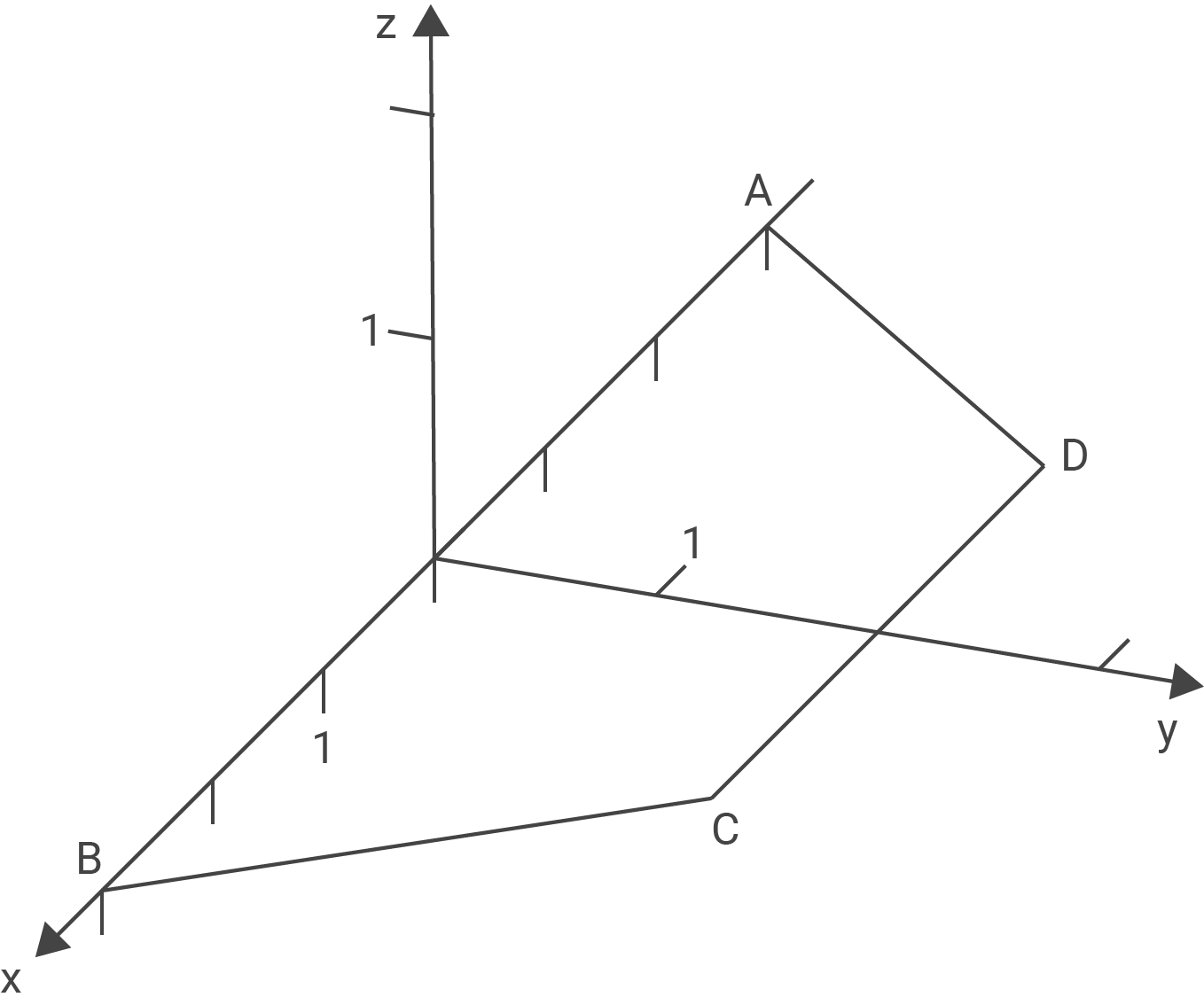
3D-Diagramm mit Punkten A, B, C, D und Achsen x, y, z. Linien und Maße sind eingezeichnet.

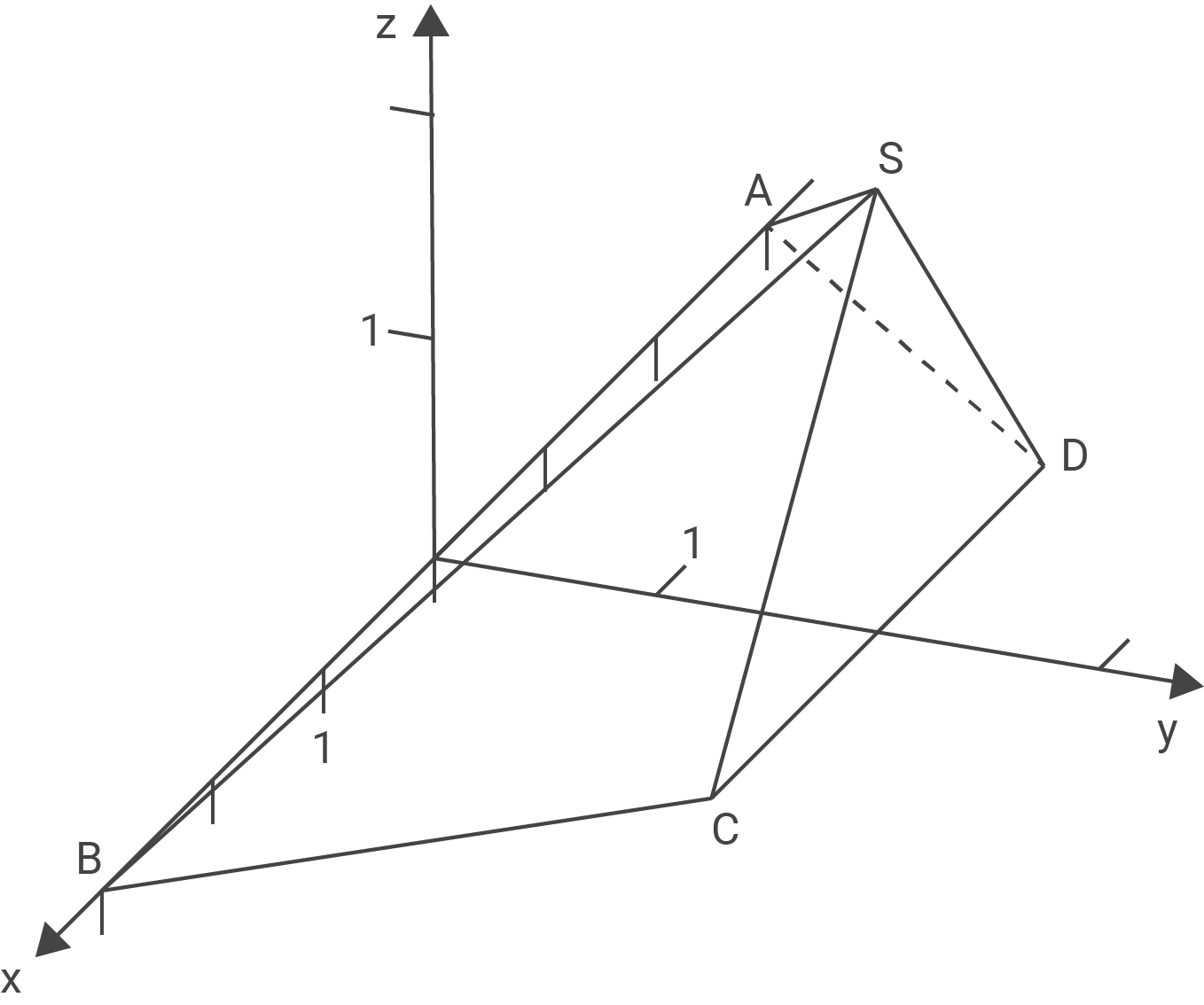
Stelle die Pyramide im Koordinatensystem der Abbildung grafisch dar.
Begründe, dass das Dreieck $SCD$ gleichschenklig ist.

(5 BE)

Die Gerade

$g: \overrightarrow{x}= \pmatrix{-3\\0\\0}+ u \cdot \pmatrix{21\\10\\2}$ , $u\in \mathbb{R}$ ,

verläuft durch den Punkt $A$ und schneidet die Pyramidenkante $\overline{CS}$ .
Berechne den Winkel, den die Gerade $g$ mit der Grundfläche $ABCD$ der Pyramide einschließt.
Berechne, in welchem Verhältnis die Gerade $g$ die Pyramidenkante $\overline{CS}$ teilt.

(7 BE)

Betrachtet werden Pyramiden mit der Grundfläche $ABCD$ , bei denen die Pyramidenspitze in Abhängigkeit von $k$ durch $S_{k}\left(0 \,\bigg \vert \, 4-\dfrac{4}{5}k \,\bigg \vert \, \dfrac{4}{5}k\right)$ beschrieben werden kann.
Untersuche, ob es Pyramiden gibt, bei denen das Dreieck $ABS_{k}$ am Punkt $S_{k}$ rechtwinklig ist.

(5 BE)

Pyramide im Koordinatensystem:

Dreidimensionale geometrische Darstellung mit Punkten A, B, C, D, S und Achsen x, y, z.

Dreieck $SCD$ auf Gleichschenkligkeit überprüfen:

Das Dreieck $SCD$ ist ein gleichschenkliges Dreieck, falls mindestens zwei Seiten gleich lang sind.
Berechne jeweils die Längen der drei Seiten $|\overrightarrow{SC}|$ , $|\overrightarrow{SD}|$ und $|\overrightarrow{CD}|$ .

$\begin{array}[t]{rll} |\overrightarrow{SC}|&=&\sqrt{(1,5-0)^2+(2-2)^2+ (0-2)^2}&\quad \\[5pt] &=&\sqrt{\dfrac{25}{4}}&\quad \\[5pt] &=&\dfrac{5}{2}&\quad \\[5pt] |\overrightarrow{SD}|&=&\sqrt{(-1,5-0)^2+(2-2)^2+ (0-2)^2}&\quad \\[5pt] &=&\sqrt{\dfrac{25}{4}}&\quad \\[5pt] &=&\dfrac{5}{2}&\quad \\[5pt] |\overrightarrow{CD}|&=&\sqrt{(-1,5-1,5)^2+(2-2)^2+ (0-0)^2}&\quad \\[5pt] &=&\sqrt{9}&\quad \\[5pt] &=&3&\quad \\[5pt] \end{array}$

$|\overrightarrow{SC}|=|\overrightarrow{SD}|$

Daraus folgt, dass das Dreieck $SCD$ gleichschenklig ist.

$g: \overrightarrow{x}= \pmatrix{-3\\0\\0}+ u \cdot \pmatrix{21\\10\\2}$ , $u\in \mathbb{R}$

Winkel berechnen, den die Gerade $g$ mit der Grundfläche $ABCD$ der Pyramide einschließt:

Die Grundfläche $ABCD$ liegt in der xy-Ebene.

Normalenvektor der xy-Ebene: $\overrightarrow{n}=\pmatrix{0\\0\\1}$

Richtungsvektor der Geraden $g$ :

$\overrightarrow{v}=\pmatrix{21\\10\\2}$

$\alpha\approx 4,91^{\circ}$

Vollständige Lösung anzeigen

Die Gerade $g$ schließt mit der Grundfläche $ABCD$ der Pyramide einen Winkel von $\alpha\approx4,91^{\circ}$ ein.

Verhältnis bestimmen, in dem die Gerade $g$ die Pyramidenkante $\overline{CS}$ teilt:

Die Pyramidenkante $\overline{CS}$ liegt auf der Geraden $h$ .

$h: \overrightarrow{x}= \overrightarrow{OC}+ l \cdot \overrightarrow{CS}$ , $\, \, l\in \mathbb{R}$

$h: \overrightarrow{x}= \pmatrix{1,5\\2\\0}+ l \cdot \pmatrix{-1,5\\0\\2}$

Schnittpunkt der Geraden $g$ und $h$ bestimmen:

$u \cdot \pmatrix{21\\10\\2}- l \cdot \pmatrix{-1,5\\0\\2}=\pmatrix{4,5\\2\\0}$

Vollständige Lösung anzeigen

Lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&10u + 1,5l&=&4,5 &\quad \\ \text{II}\quad&10u&=& 2 &\quad \\ \text{III}\quad&2u-2l&=& 0 &\quad \\ \end{array}$

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} 10u&=&2 &\quad \scriptsize \mid\; :10 \\[5pt] u&=&\dfrac{1}{5} \end{array}$

$u=\dfrac{1}{5}$ in die erste bzw. dritte Zeile einsetzen.

Einsetzen in die dritte Zeile liefert:

$\begin{array}[t]{rll} 2 \cdot \dfrac{1}{5}-2l&=&0 &\quad \scriptsize \mid\;-\dfrac{2}{5} \\[5pt] -2l&=&-\dfrac{2}{5} &\quad \scriptsize \mid\;:(-2)\\[5pt] l&=&\dfrac{1}{5}&\quad \\[5pt] \end{array}$

$u=\dfrac{1}{5}$ in die Geradengleichung $g$ bzw. $l=\dfrac{1}{5}$ in die Geradengleichung $h$ einsetzen, liefert den Ortsvektor $\overrightarrow{OP}$ des Schnittpunkts.

$\begin{array}[t]{rll} \overrightarrow{OP}&=&\pmatrix{1,5\\2\\0}+ \dfrac{1}{5} \cdot \pmatrix{-1,5\\0\\2} &\quad \\[5pt] &=&\pmatrix{\dfrac{6}{5}\\2\\\dfrac{2}{5}} \end{array}$

Die Gerade $g$ schneidet die Pyramidenkante $\overline{CS}$ im Punkt $P\left(\dfrac{6}{5}\,\bigg \vert \,2 \,\bigg \vert \, \dfrac{2}{5}\right)$ .

$\begin{array}[t]{rll} |\overrightarrow{CS}|&=&|\overrightarrow{CP}|+|\overrightarrow{SP}| &\quad \\[5pt] |\overrightarrow{CP}|&=&\sqrt{(\dfrac{6}{5}-1,5)^2+(2-2)^2+ (\dfrac{2}{5}-0)^2} &\quad \\[5pt] &=&\sqrt{\dfrac{9}{100}+0+\dfrac{4}{25}} &\quad \\[5pt] &=&\sqrt{\dfrac{1}{4}} &\quad \\[5pt] &=& \dfrac{1}{2}&\quad \\[5pt] |\overrightarrow{SP}|&=&\sqrt{(\dfrac{6}{5}-0)^2+(2-2)^2+ (\dfrac{2}{5}-2)^2} &\quad \\[5pt] &=&\sqrt{\dfrac{36}{25}+0+\dfrac{64}{25}} &\quad \\[5pt] &=&\sqrt{4} &\quad \\[5pt] &=& 2&\quad \\[5pt] |\overrightarrow{CS}|&=&|\overrightarrow{CP}|+|\overrightarrow{SP}| &\quad \\[5pt] &=&\dfrac{1}{2}+2 &\quad \\[5pt] &=&2,5 &\quad \\[5pt] \end{array}$

Die Gerade $g$ teilt die Pyramidenkante $\overline{CS}$ im Verhältnis $1:4$ .

Werte für $k$ , sodass das Dreieck $ABS_{k}$ am Punkt $S_k$ rechtwinklig ist:

Das Dreieck $ABS_k$ ist am Punkt $S_k$ rechtwinklig, wenn $\overrightarrow{S_kA}$ und $\overrightarrow{S_kB}$ im rechten Winkel zueinander stehen, das heißt, dass das Skalarprodukt der beiden Vektoren $0$ ergibt.

Es muss gelten: $\overrightarrow{S_kA}\circ \overrightarrow{S_kB} = 0$

$\begin{array}[t]{rll} \overrightarrow{S_kA}&=&\pmatrix{-3\\-4+\dfrac{4}{5}k\\-\dfrac{4}{5}k} &\quad \\[5pt] \overrightarrow{S_kB}&=&\pmatrix{3\\-4+\dfrac{4}{5}k\\-\dfrac{4}{5}k} &\quad \\[5pt] \end{array}$

$\overrightarrow{S_kA}\circ \overrightarrow{S_kB}=7-\frac{32}{5}k+\frac{32}{25}k^2$

Vollständige Lösung anzeigen

$\overrightarrow{S_kA}\circ \overrightarrow{S_kB} = 0$ , falls $\dfrac{32}{25}k^2-\dfrac{32}{5}k+7=0$ .
Mögliche Werte für $k$ entsprechen den Nullstellen von $\dfrac{32}{25}k^2-\dfrac{32}{5}k+7=0$ .

$\begin{array}[t]{rll} \dfrac{32}{25}k^2-\dfrac{32}{5}k+7&=&0 &\quad \scriptsize \mid\; \cdot \dfrac{25}{32}\\[5pt] k^2-5k+ \dfrac{175}{32}&=&0 \end{array}$

Die Nullstellen können mit Hilfe der pq-Formel berechnet werden.

pq-Formel:

$\begin{array}[t]{rll} k_{1, 2}&=&\dfrac{5}{2}\pm \sqrt{\dfrac{25}{4}-\dfrac{175}{32}} &\quad \\[5pt] &=&\dfrac{5}{2}\pm \sqrt{\dfrac{25}{32}} &\quad \\[5pt] &=&\dfrac{5}{2}\pm \dfrac{5 \sqrt{2}}{8} &\quad \\[5pt] k_1&=&\dfrac{5}{2}+ \dfrac{5 \sqrt{2}}{8} &\quad \\[5pt] &=&\dfrac{20+5\sqrt{2}}{8} &\quad \\[5pt] k_2&=&\dfrac{5}{2}- \dfrac{5 \sqrt{2}}{8} &\quad \\[5pt] &=&\dfrac{20-5\sqrt{2}}{8} &\quad \\[5pt] \end{array}$

Für $k_1=\dfrac{20+5\sqrt{2}}{8}$ und $k_2=\dfrac{20-5\sqrt{2}}{8}$ gibt es Pyramiden, sodass das Dreieck $ABS_k$ am Punkt $S_k$ rechtwinklig ist.