Aufgabe 1A
Ein Unternehmen verkauft Fitnessarmbänder. Die momentane Änderungsrate des Absatzes wird beschrieben mit der in  definierten Funktion
definierten Funktion  mit:
mit:
 Dabei ist
Dabei ist  die seit der Produkteinführung vergangene Zeit in Monaten und
die seit der Produkteinführung vergangene Zeit in Monaten und  die momentane Änderungsrate des Absatzes in Stück pro Monat.
die momentane Änderungsrate des Absatzes in Stück pro Monat.
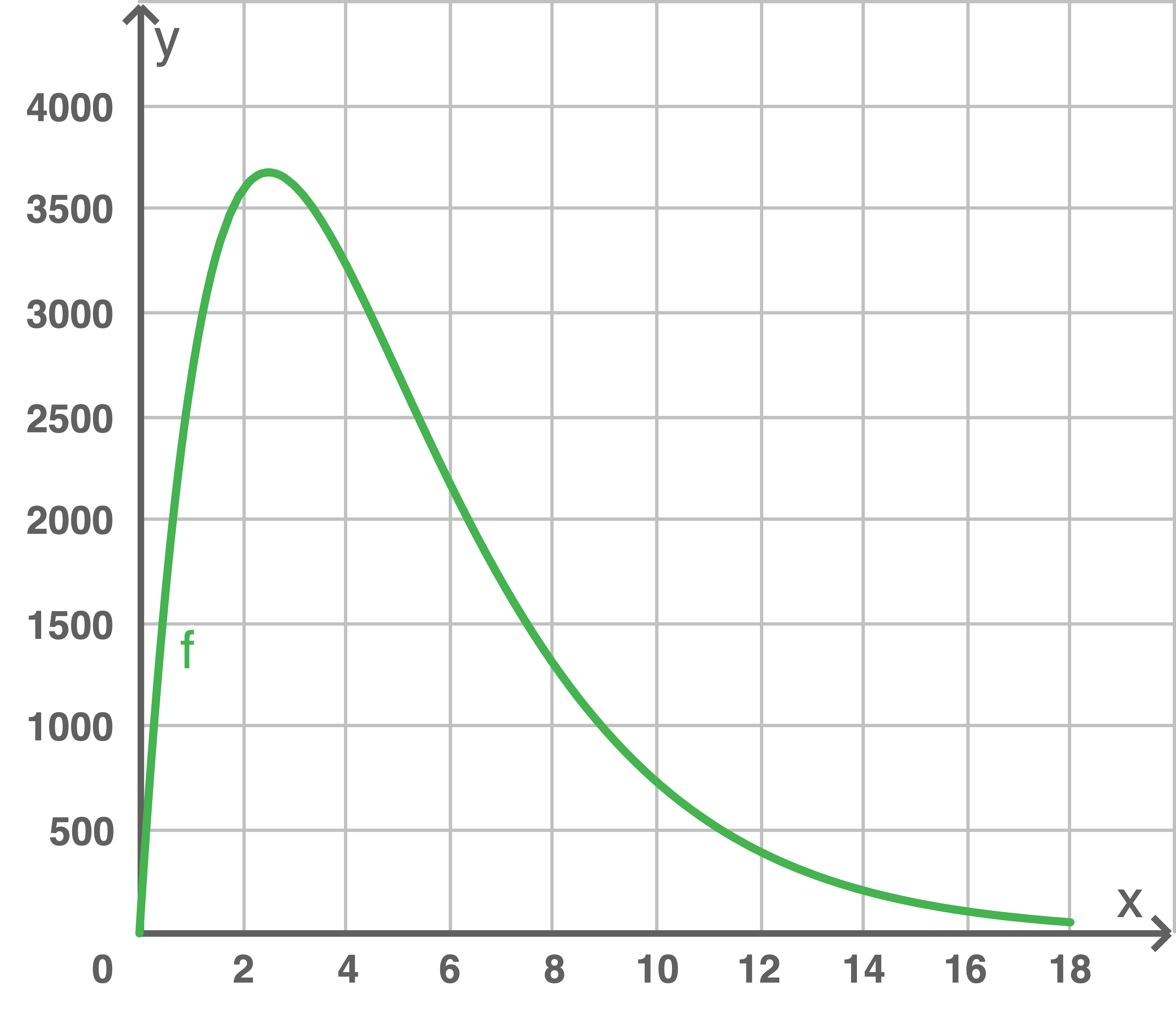
a)
Berechne den Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes den größten Wert erreicht, und gib diesen größten Wert an.
Kennzeichne in der Abbildung diejenigen Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören.
Kennzeichne in der Abbildung diejenigen Punkte des Graphen, die zu einer momentanen Änderungsrate des Absatzes in Höhe von 1000 Stück pro Monat gehören.
(6 BE)
b)
Im Beobachtungszeitraum gibt es einen Zeitpunkt, zu dem die momentane Änderungsrate des Absatzes am stärksten zunimmt, und einen Zeitpunkt, zu dem sie am stärksten abnimmt. Zur Bestimmung dieser beiden Zeitpunkte wurden folgende Berechnungen durchgeführt:

 Erläutere diese beiden Berechnungen.
Erläutere diese beiden Berechnungen.
Bestimme ohne weitere Rechnung die beiden gesuchten Zeitpunkte.
Gleichzeitig mit der Einführung des Fitnessarmbands brachte das Unternehmen eine Smartwatch auf den Markt. Die momentane Änderungsrate des Absatzes der Smartwatch in Stück pro Monat wird mithilfe der in
I.
II.
Bestimme ohne weitere Rechnung die beiden gesuchten Zeitpunkte.
(6 BE)
c)
Vergleiche die momentanen Änderungsraten des Absatzes für das Fitnessarmband und die Smartwatch fünf Monate nach Produkteinführung.
(2 BE)
d)
Berechne die Anzahl der im ersten Jahr nach Produkteinführung insgesamt verkauften Smartwatches.
Untersuche, ob es einen Zeitpunkt nach Produkteinführung gibt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden.
Gib gegebenenfalls diesen Zeitpunkt an.
Gegeben sind nun die in Untersuche, ob es einen Zeitpunkt nach Produkteinführung gibt, bis zu dem ebenso viele Fitnessarmbänder wie Smartwatches verkauft wurden.
Gib gegebenenfalls diesen Zeitpunkt an.
(6 BE)
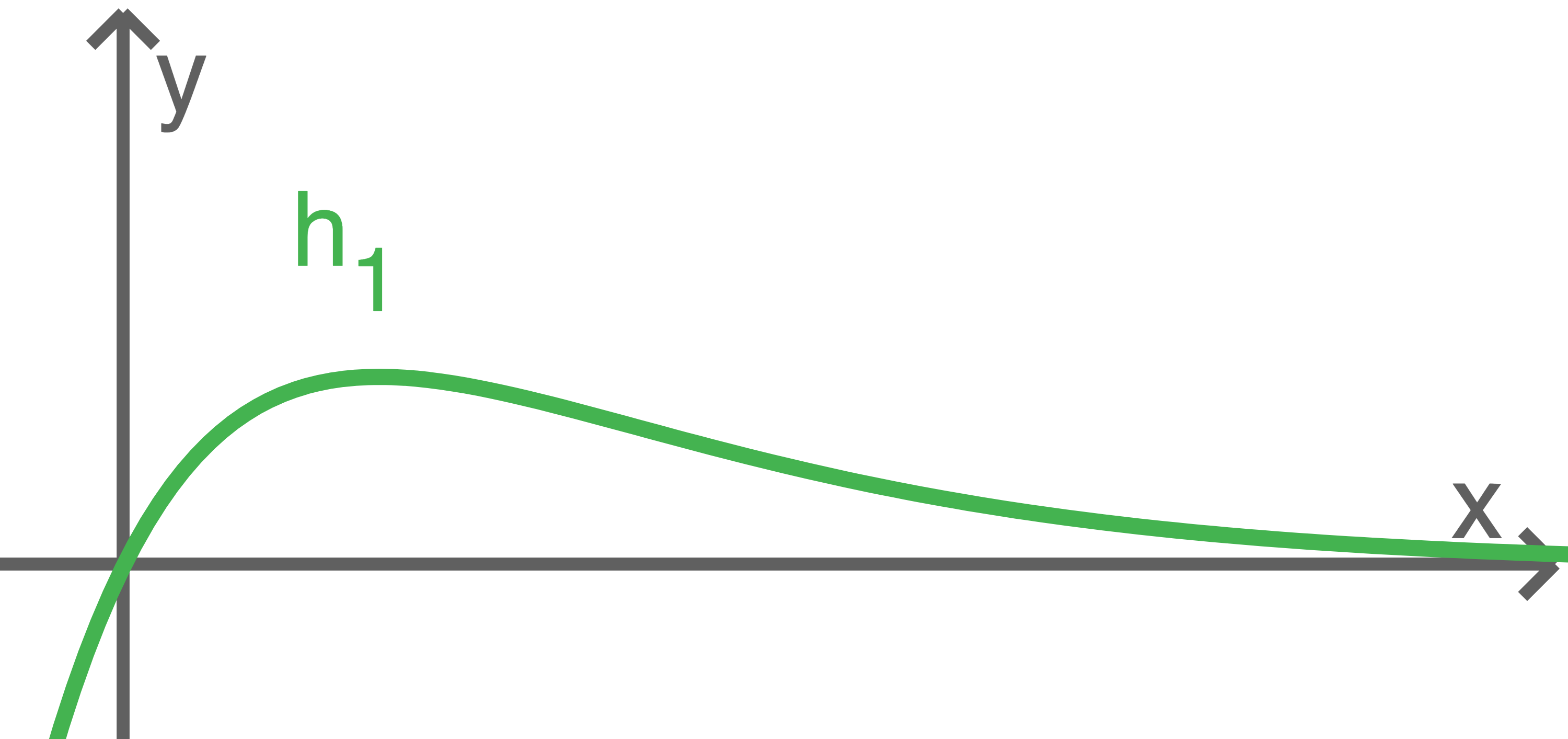
e)
Gib für den Graphen von  die Koordinaten des Extrempunktes und des Wendepunktes an.
die Koordinaten des Extrempunktes und des Wendepunktes an.
(2 BE)
f)
Die Tangente an den Graphen von  in dessen Wendepunkt und der Graph von
in dessen Wendepunkt und der Graph von  schließen mit der
schließen mit der  -Achse eine Fläche ein. Bestimme deren Flächeninhalt.
-Achse eine Fläche ein. Bestimme deren Flächeninhalt.
(6 BE)
g)
Jeder Punkt  liegt auf einer Ursprungsgeraden und jeder Punkt
liegt auf einer Ursprungsgeraden und jeder Punkt  liegt auf einer anderen Ursprungsgeraden. Gib die Gleichungen dieser beiden Ursprungsgeraden an.
liegt auf einer anderen Ursprungsgeraden. Gib die Gleichungen dieser beiden Ursprungsgeraden an.
(3 BE)
h)
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/6281c107916a78d647bb16409e7052e381096a80855f844947cf57b4b96df262?color=5a5a5a) Mit dem Satz vom Nullprodukt gilt:
Mit dem Satz vom Nullprodukt gilt:
![\(\begin{array}[t]{rll}
1-0,4\cdot x&=& 0 &\quad \scriptsize \mid\; -1 \\[5pt]
-0,4\cdot x&=& -1 &\quad \scriptsize \mid\; :(-0,4) \\[5pt]
x&=&2,5
\end{array}\)](https://mathjax.schullv.de/65c0e5a6aa5198d09165d77cf8dbb388007f2349de83e199cc2bbac159687142?color=5a5a5a) Es ist
Es ist  , deshalb ist
, deshalb ist  die einzige Extremstelle.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Nach der Produktregel ist
die einzige Extremstelle.
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Nach der Produktregel ist  .
.
 3. Schritt:
3. Schritt:  ermitteln
ermitteln
 Die momentane Änderungsrate des Absatzes erreicht zweieinhalb Monate nach Produkteinführung mit ungefähr
Die momentane Änderungsrate des Absatzes erreicht zweieinhalb Monate nach Produkteinführung mit ungefähr  Stück pro Monat den größten Wert.
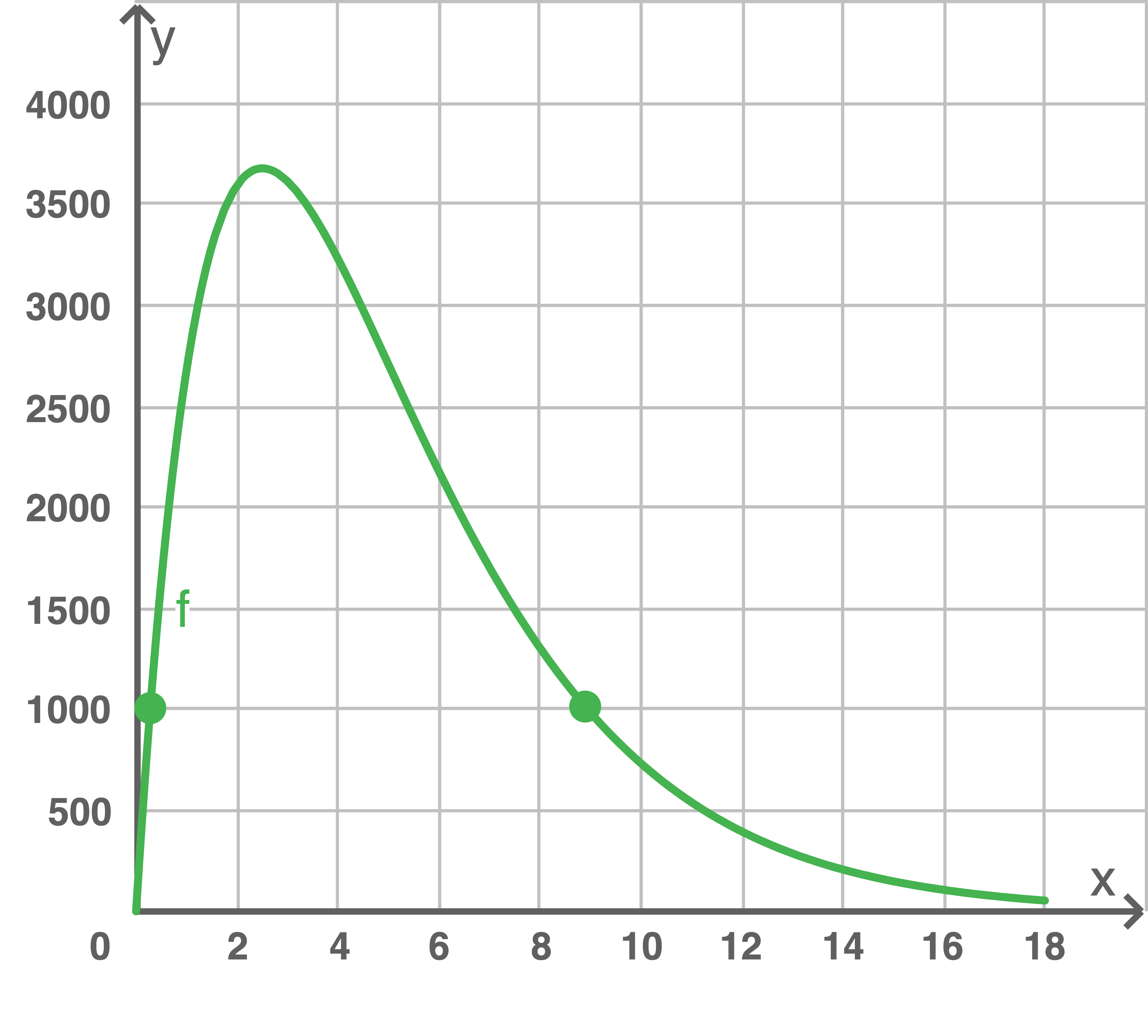
Kennzeichnung in der Abbildung
Stück pro Monat den größten Wert.
Kennzeichnung in der Abbildung

b)
Die gesuchten Zeitpunkte sind durch die globalen Extremstellen der Ableitungsfunktion  im Intervall
im Intervall ![\([0;18]\)](https://mathjax.schullv.de/e8e9fe9ed19539c81417a22651f2286708601f9b50fd50615a26fa465a3ca531?color=5a5a5a) gegeben, bei denen es sich um lokale Extremstellen oder Randstellen handeln kann.
Mit der Berechnung werden zunächst die lokalen Extremstellen von
gegeben, bei denen es sich um lokale Extremstellen oder Randstellen handeln kann.
Mit der Berechnung werden zunächst die lokalen Extremstellen von  ermittelt:
ermittelt:  ist die einzige Nullstelle der Funktion
ist die einzige Nullstelle der Funktion  und damit die einzige mögliche lokale Extremstelle von
und damit die einzige mögliche lokale Extremstelle von  Da zusätzlich
Da zusätzlich  gilt, ist
gilt, ist  eine lokale Minimalstelle von
eine lokale Minimalstelle von  .
.  ist als einzige lokale Extremstelle von
ist als einzige lokale Extremstelle von  auch die globale Minimalstelle von
auch die globale Minimalstelle von  Da außerdem der Graph von
Da außerdem der Graph von  an der Stelle
an der Stelle  fällt, gilt: Fünf Monate nach der Produkteinführung nimmt die momentane Änderungsrate des Absatzes am stärksten ab. Da der Graph von
fällt, gilt: Fünf Monate nach der Produkteinführung nimmt die momentane Änderungsrate des Absatzes am stärksten ab. Da der Graph von  an der Randstelle
an der Randstelle  steigt und an der Randstelle
steigt und an der Randstelle  fällt, gilt
fällt, gilt  und
und  Daher ist
Daher ist  die globale Maximalstelle von
die globale Maximalstelle von  . Die momentane Änderungsrate des Absatzes nimmt zum Zeitpunkt der Produkteinführung am stärksten zu.
. Die momentane Änderungsrate des Absatzes nimmt zum Zeitpunkt der Produkteinführung am stärksten zu.
c)
Mit dem Taschenrechner ergibt sich:

 Fünf Monate nach Produkteinführung ist die momentane Änderungsrate des Absatzes für die Smartwatch etwa doppelt so groß wie die für das Armband.
Fünf Monate nach Produkteinführung ist die momentane Änderungsrate des Absatzes für die Smartwatch etwa doppelt so groß wie die für das Armband.
d)
Mit dem Taschenrechner ergibt sich:
 Im ersten Jahr nach der Produkteinführung werden ungefähr
Im ersten Jahr nach der Produkteinführung werden ungefähr  Smartwatches verkauft.
Die Anzahl an verkauften Geräten kann jeweils mit einem Integral berechnet werden:
Anzahl der verkauften Smartwatches bis zum Zeitpunkt
Smartwatches verkauft.
Die Anzahl an verkauften Geräten kann jeweils mit einem Integral berechnet werden:
Anzahl der verkauften Smartwatches bis zum Zeitpunkt 
 Anzahl der verkauften Fitnessarmbänder bis zum Zeitpunkt
Anzahl der verkauften Fitnessarmbänder bis zum Zeitpunkt 

![\(\begin{array}[t]{rll}
A_S&=& A_F \\[5pt]
\displaystyle\int_{0}^{t}f(x)\;\mathrm dx&=& \displaystyle\int_{0}^{t}g(x)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/4a373c1d73210dc432a150f394dac82486a9339e681da5d3a663a0a277d6519b?color=5a5a5a) Mit dem Taschenrechner kann für
Mit dem Taschenrechner kann für  für diese Gleichung die Lösung
für diese Gleichung die Lösung  gefunden werden.
Etwa viereinhalb Monate nach Produkteinführung stimmt die Anzahl der seit der Produkteinführung verkauften Fitnessarmbänder mit der Anzahl der seit der Produkteinführung verkauften Smartwatches überein.
gefunden werden.
Etwa viereinhalb Monate nach Produkteinführung stimmt die Anzahl der seit der Produkteinführung verkauften Fitnessarmbänder mit der Anzahl der seit der Produkteinführung verkauften Smartwatches überein.
e)
Einsetzen von  in die in der Aufgabenstellung gegebenen Punkte ergibt:
in die in der Aufgabenstellung gegebenen Punkte ergibt:
 und
und 
f)
Bestimmen der Steigung des Graphen von  an der Wendestelle
an der Wendestelle  mit dem Taschenrechner ergibt:
mit dem Taschenrechner ergibt:  Auflösen der Tangentengleichung:
Auflösen der Tangentengleichung:
![\(\begin{array}[t]{rll}
t(x) &=& h_1](https://mathjax.schullv.de/0bc9d1b60bc1479aa1b530a3213c3645a840a2c60048bc2e0e869d56d891471a?color=5a5a5a) Die Nullstelle des Graphen von
Die Nullstelle des Graphen von  kann mit dem Taschenrechner bestimmt werden und beträgt:
kann mit dem Taschenrechner bestimmt werden und beträgt:  Der gesuchte Flächeninhalt beträgt:
Der gesuchte Flächeninhalt beträgt:
![\(\begin{array}[t]{rll}
A &=& \displaystyle\int_{0}^{20}h_1(x) + \displaystyle\int_{20}^{40}t(x) \;\mathrm dx \\[5pt]
A &\approx& 59,4 + \dfrac{1}{2} \cdot 20 \cdot \dfrac{20}{\mathrm{e}^2} \;\mathrm dx \\[5pt]
A&\approx& = 86,47
\end{array}\)](https://mathjax.schullv.de/838d25c41552f8b67ce352584ded511f5f8b6939c061325fca02cc4cb0042c77?color=5a5a5a)
g)
Ortskurve für die Extrempunkte aufstellen
Aus den Koordinaten der Extrempunkte folgt  und
und 
![\(\begin{array}[t]{rll}
x&=&\dfrac{10}{b} \\[5pt]
b&=&\dfrac{10}{x} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/14a2e87e955c257fcd37a7851414787abf8d3b351566849b0488425a58175ba3?color=5a5a5a) Eingesetzt in
Eingesetzt in  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
y &=&\dfrac{10}{\dfrac{10}{x}}\cdot \mathrm e^{-1} \\[5pt]
y&=& \dfrac{1}{\mathrm e} x
\end{array}\)](https://mathjax.schullv.de/35fde5533e34465005d00db8c7449a6d614411e14bbccc26d20f9c8bec473003?color=5a5a5a) Gerade, auf der die Extrempunkte liegen:
Gerade, auf der die Extrempunkte liegen:  Ortskurve für die Wendepunkte aufstellen
Aus den Koordinaten der Wendepunkte folgt
Ortskurve für die Wendepunkte aufstellen
Aus den Koordinaten der Wendepunkte folgt  und
und 
![\(\begin{array}[t]{rll}
x&=&\dfrac{20}{b} \\[5pt]
b&=&\dfrac{20}{x} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b0d9e06b645931638be2ca4a6b44b9124908fdca23e9518fa99b72115a2f0710?color=5a5a5a) Eingesetzt in
Eingesetzt in  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
y &=&\dfrac{20}{\dfrac{20}{x}}\cdot \mathrm e^{-2} \\[5pt]
y&=& \dfrac{1}{\mathrm e^2} x
\end{array}\)](https://mathjax.schullv.de/24b0b0750310524164def0d361decc2c655df36780d5567d5094256c3552b380?color=5a5a5a) Gerade, auf der die Wendepunkte liegen:
Gerade, auf der die Wendepunkte liegen: 
h)
Für beliebige Werte von  geht das Dreieck
geht das Dreieck  aus dem entsprechenden Dreieck für
aus dem entsprechenden Dreieck für  durch Streckung mit dem Faktor
durch Streckung mit dem Faktor  hervor, wobei das Streckzentrum im Koordinatenursprung liegt.
Daher sind alle Dreiecke
hervor, wobei das Streckzentrum im Koordinatenursprung liegt.
Daher sind alle Dreiecke  ähnlich.
ähnlich.