Aufgabe 1C
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Der Graph von
Der Graph von  besitzt zwei Extrempunkte. Einer davon hat die
besitzt zwei Extrempunkte. Einer davon hat die  -Koordinate
-Koordinate  Der Graph von
Der Graph von  hat den Wendepunkt
hat den Wendepunkt 
 soll in drei Schritten verändert werden. Die drei Schritte sind:
soll in drei Schritten verändert werden. Die drei Schritte sind:
a)
Begründe, dass der Graph von  symmetrisch bezüglich seines Wendepunktes ist.
Bestimme die Koordinaten der Schnittpunkte des Graphen von
symmetrisch bezüglich seines Wendepunktes ist.
Bestimme die Koordinaten der Schnittpunkte des Graphen von  mit den Koordinatenachsen.
mit den Koordinatenachsen.
(5 BE)
b)
Es gibt Punkte des Graphen von  in denen die Tangente an den Graphen von
in denen die Tangente an den Graphen von  parallel zur Geraden durch die beiden Extrempunkte des Graphen von
parallel zur Geraden durch die beiden Extrempunkte des Graphen von  ist.
Bestimme die Koordinaten dieser Punkte.
ist.
Bestimme die Koordinaten dieser Punkte.
(6 BE)
c)
Bestimme alle Werte für  sodass der Graph zu
sodass der Graph zu  genau zwei Nullstellen besitzt.
genau zwei Nullstellen besitzt.
(4 BE)
d)
Die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  hat die Gleichung
hat die Gleichung  .
.
Der Graph von und die Tangente
und die Tangente  schließen eine Fläche ein.
Bestimme den Inhalt dieser Fläche.
schließen eine Fläche ein.
Bestimme den Inhalt dieser Fläche.
Der Graph von Der Graph von
(4 BE)
- Spiegeln an der
-Achse
- Verschieben um 6 in positive
-Richtung
- Verschieben um 14 in positive
-Richtung
e)
Gib an, wie viele verschiedene neue Graphen entstehen, nachdem die drei Schritte in allen möglichen Reihenfolgen ausgeführt wurden.
Begründe deine Angabe.
(5 BE)
Wird der Graph von  den drei Schritten in der angegebenen Reihenfolge unterzogen, so entsteht der Graph der in
den drei Schritten in der angegebenen Reihenfolge unterzogen, so entsteht der Graph der in  definierten Funktion
definierten Funktion  mit
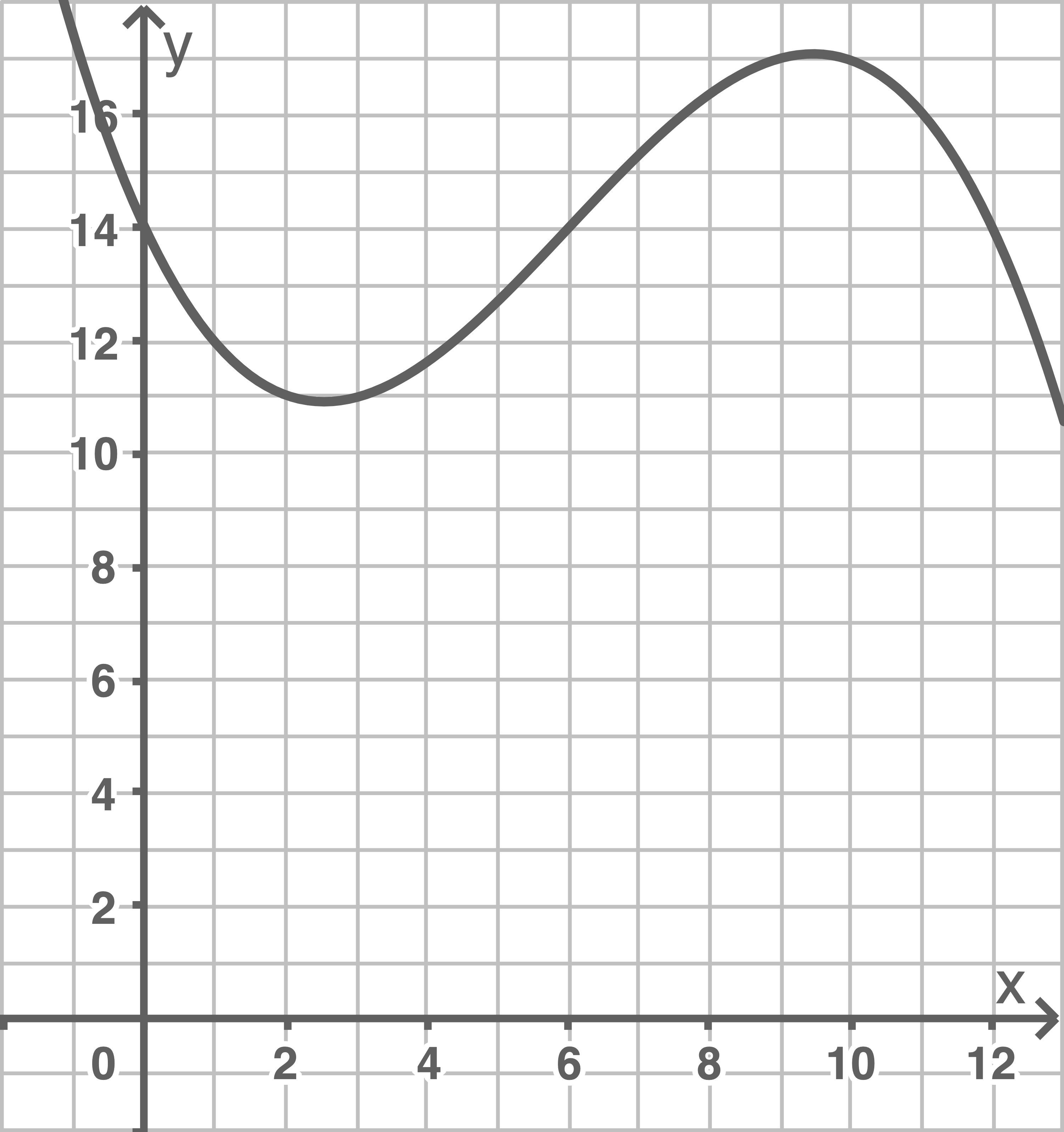
mit  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von  .
Die Funktion
.
Die Funktion  beschreibt für
beschreibt für  den Verlauf der Tagesdurchschnittstemperatur an einem bestimmten Ort.
Dabei ist
den Verlauf der Tagesdurchschnittstemperatur an einem bestimmten Ort.
Dabei ist  die seit einem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und
die seit einem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und  die Temperatur in
die Temperatur in  .
.

f)
Gib die Bedeutung der Wendestelle von  hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an.
hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an.
(3 BE)
g)
Die folgenden Rechnungen stellen in Verbindung mit der Abbildung die Lösung einer Aufgabe im Sachzusammenhang dar:
Gib eine passende Aufgabenstellung an.
Erläutere den dargestellten Lösungsweg.
(5 BE)
h)
Entscheide, ob die Funktion  für
für  geeignet ist, den Verlauf der Tagesdurchschnittstemperatur an dem betrachteten Ort für ein weiteres Jahr zu beschreiben.
Begründe deine Entscheidung.
geeignet ist, den Verlauf der Tagesdurchschnittstemperatur an dem betrachteten Ort für ein weiteres Jahr zu beschreiben.
Begründe deine Entscheidung.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Symmetrie begründen
Der Funktionsterm von  ist ganzrational und enthält Potenzen von
ist ganzrational und enthält Potenzen von  mit ausschließlich ungeraden Exponenten. Somit ist der Graph von
mit ausschließlich ungeraden Exponenten. Somit ist der Graph von  punktsymmetrisch zum Ursprung, also seinem Wendepunkt.
Koordinaten bestimmen
Der Schnittpunkt des Graphen von
punktsymmetrisch zum Ursprung, also seinem Wendepunkt.
Koordinaten bestimmen
Der Schnittpunkt des Graphen von  mit der
mit der  -Achse ist bereits durch den Wendepunkt gegeben und besitzt somit die Koordinaten
-Achse ist bereits durch den Wendepunkt gegeben und besitzt somit die Koordinaten  Für die Schnittpunkte mit der
Für die Schnittpunkte mit der  -Achse gilt:
-Achse gilt:
![\(\begin{array}[t]{rll}
f(x)&=& 0 & \\[5pt]
\dfrac{1}{27} x^3-\dfrac{4}{3} x &=& 0
\end{array}\)](https://mathjax.schullv.de/78ae966a68aa4c93141db39f75be07421a9d5f24c96bcc7a1ebf7eaa7099eac1?color=5a5a5a) Mit dem solve-Befehl des GTR folgen die Schnittstellen des Graphen von
Mit dem solve-Befehl des GTR folgen die Schnittstellen des Graphen von  mit der
mit der  -Achse mit
-Achse mit 
 und
und  Die Koordinaten der Schnittpunkte ergeben sich also zu
Die Koordinaten der Schnittpunkte ergeben sich also zu 
 und
und 
b)
1. Schritt: Extrempunkte bestimmen
Da der Graph von  symmetrisch bezüglich seines Wendepunkts ist und einer der beiden Extrempunkte die
symmetrisch bezüglich seines Wendepunkts ist und einer der beiden Extrempunkte die  -Koordinate
-Koordinate  besitzt, folgt, dass der zweite Extrempunkt die
besitzt, folgt, dass der zweite Extrempunkt die  -Koordinate
-Koordinate  hat.
hat.
 -Koordinaten berechnen:
-Koordinaten berechnen:
![\(\begin{array}[t]{rll}
f(\sqrt{12})&=& \dfrac{1}{27} \cdot \sqrt{12}^3-\dfrac{4}{3} \cdot \sqrt{12} & \\[5pt]
&\approx& -3,08
\end{array}\)](https://mathjax.schullv.de/d00bc19a34fdf05d88a60d596d11729b5f29f82de56624463e203a4a337b90f4?color=5a5a5a) Die Koordinaten der Extrempunkte sind somit gegeben durch
Die Koordinaten der Extrempunkte sind somit gegeben durch  und
und  2. Schritt: Steigung bestimmen
Für die Steigung der Geraden durch die beiden Extrempunkte gilt:
2. Schritt: Steigung bestimmen
Für die Steigung der Geraden durch die beiden Extrempunkte gilt:
![\(\begin{array}[t]{rll}
m&=& \dfrac{f(\sqrt{12})-f(-\sqrt{12})}{\sqrt{12}-(-\sqrt{12})} & \\[5pt]
&=& \dfrac{-3,08-3,08}{\sqrt{12}+\sqrt{12}} & \\[5pt]
&\approx& -0,89
\end{array}\)](https://mathjax.schullv.de/f8264f8caa89106fc0254b7bd3e804c0433045e88fc472534dbbf16d895b94d8?color=5a5a5a) 3. Schritt: Punkte ermitteln
Für die Punkte des Graphen von
3. Schritt: Punkte ermitteln
Für die Punkte des Graphen von  in denen die Tangente an den Graphen parallel zur Geraden durch die beiden Extrempunkte ist, muss die Steigung der Tangente folglich der Steigung der Geraden entsprechen.
Es soll also gelten:
in denen die Tangente an den Graphen parallel zur Geraden durch die beiden Extrempunkte ist, muss die Steigung der Tangente folglich der Steigung der Geraden entsprechen.
Es soll also gelten:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/4bb39c0d0a7f95d977ed84bc377f6bbf3b94ffa32b3b70d9c7a27a26174de68f?color=5a5a5a) Der GTR liefert
Der GTR liefert  und
und 
 -Koordinaten bestimmen:
-Koordinaten bestimmen:
![\(\begin{array}[t]{rll}
f(2)&=& \dfrac{1}{27} \cdot 2^3-\dfrac{4}{3} \cdot 2 & \\[5pt]
&\approx& -2,4
\end{array}\)](https://mathjax.schullv.de/3fcb82775d16e7270a5261e26081167356a2ce10a5dcc3f85cc84bfc84e4778d?color=5a5a5a) Aufgrund der Symmetrie folgt
Aufgrund der Symmetrie folgt  Die Koordinaten der Punkte ergeben sich somit zu
Die Koordinaten der Punkte ergeben sich somit zu  und
und 
c)
Der Graph von  muss parallel zur
muss parallel zur  -Achse so verschoben werden, dass einer der Extrempunkte auf der
-Achse so verschoben werden, dass einer der Extrempunkte auf der  -Achse liegt.
Es ergeben sich also:
-Achse liegt.
Es ergeben sich also:


d)
Schnittstellen bestimmen:
![\(\begin{array}[t]{rll}
f(x)&=& t(x) & \\[5pt]
\dfrac{1}{27} x^3-\dfrac{4}{3} x&=& \dfrac{8}{3} x-16
\end{array}\)](https://mathjax.schullv.de/997b5b80b0b3aaa5f3a0ed077168fbb423bd235076e3d35ece8df79ef4504fb8?color=5a5a5a) Der GTR liefert
Der GTR liefert  und
und  Der Inhalt der Fläche folgt nun mit:
Der Inhalt der Fläche folgt nun mit:
e)
Anzahl angeben
Es entstehen zwei neue Graphen.
Angabe begründen
Das Ergebnis der Veränderungen ist unabhängig von der Position der Verschiebung in  -Richtung. Wesentlich ist nur die Reihenfolge der beiden anderen Schritte.
-Richtung. Wesentlich ist nur die Reihenfolge der beiden anderen Schritte.
Für diese gibt es genau zwei mögliche Reihenfolgen der Ausführung und somit zwei neue Graphen.
Für diese gibt es genau zwei mögliche Reihenfolgen der Ausführung und somit zwei neue Graphen.
f)
Die Wendestelle gibt den Zeitpunkt mit dem größten Anstieg der Tagesdurchschnittstemperatur an.
g)
Aufgabenstellung angeben
Ermittle die Differenz zwischen der höchsten und der niedrigsten Tagesdurchschnittstemperatur.
Lösungsweg erläutern
In der ersten Zeile werden die möglichen Extremstellen von  bestimmt. Anhand der Abbildung wird ersichtlich, dass diese Stellen tatsächlich absolute Extremstellen im Modellierungsbereich sind.
In der zweiten Zeile wird die Differenz zwischen den zugehörigen Funktionswerten berechnet.
bestimmt. Anhand der Abbildung wird ersichtlich, dass diese Stellen tatsächlich absolute Extremstellen im Modellierungsbereich sind.
In der zweiten Zeile wird die Differenz zwischen den zugehörigen Funktionswerten berechnet.
h)
Die Funktion ist nicht geeignet.
Einsetzen von Werten von  mit
mit  in
in  liefert beispielsweise
liefert beispielsweise  was den realen Gegebenheiten widerspricht.
Für die Tagesdurchschnittstemperaturen über mehrere Jahre hinweg ist außerdem ein annähernd periodischer Temperaturverlauf zu erwarten,
was den realen Gegebenheiten widerspricht.
Für die Tagesdurchschnittstemperaturen über mehrere Jahre hinweg ist außerdem ein annähernd periodischer Temperaturverlauf zu erwarten,  ist jedoch nicht periodisch.
ist jedoch nicht periodisch.