Aufgabe 2A

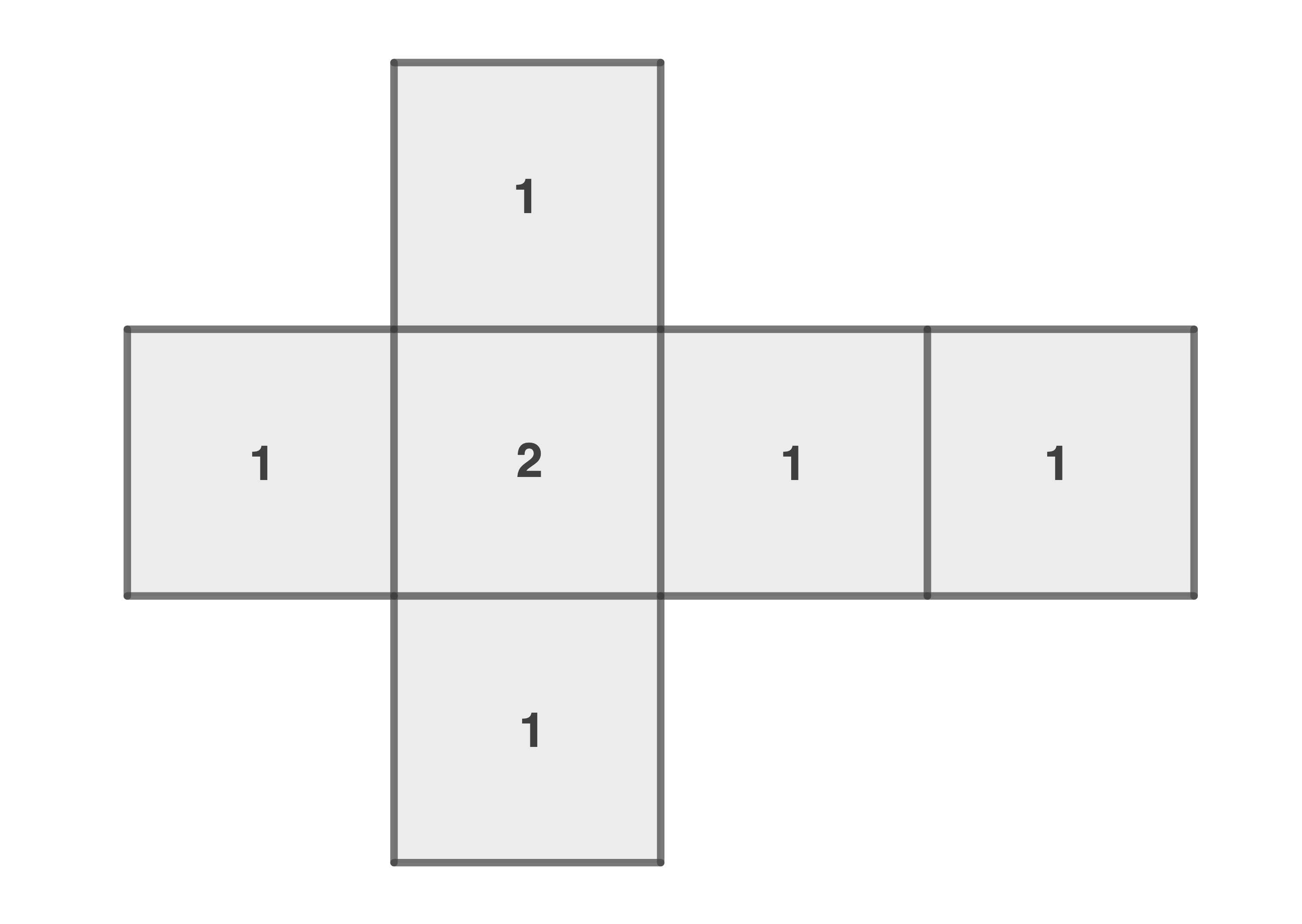
Ein Würfelspiel wird mit einem Würfel gespielt, dessen Netz in der Abbildung dargestellt ist.

Der Spieler zahlt einen Einsatz von $3\,€$ und würfelt dann zweimal. Anschließend wird ihm die Summe der beiden gewürfelten Zahlen in $\,€$ ausgezahlt.

Diagramm mit Zahlen in verschiedenen Kästchen, dargestellt in einer Kreuzform.

Die Zufallsgröße $X$ beschreibt den Betrag in $\,€$ , der an den Spieler ausgezahlt wird.
Begründe, dass $X$ nur die Werte $2, 3$ und $4$ annehmen kann.
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von $X$ .

$k$	$P(X=k)$
$2$	$\dfrac{25}{36}$
$3$	$\dfrac{10}{36}$
$4$	$\dfrac{1}{36}$

Gib ein Ereignis an, das bezüglich dieser Verteilung mit einer Wahrscheinlichkeit von $\displaystyle \frac{26}{36}$ eintritt.
Ein Spiel heißt fair, wenn die Einsätze und die Auszahlungen auf lange Sicht ausgeglichen sind.
Untersuche, ob das Spiel fair ist.
Berechne den Zahlenwert, mit dem die „ $2$ “-Seitenfläche des Würfels überklebt werden muss, damit das Spiel bei einem Einsatz von $5\,€$ fair ist.

(11 BE)

Es wird $10$ -mal mit dem oben abgebildeten Würfel gespielt.
Berechne die Wahrscheinlichkeit dafür, dass bei mindestens $2$ Spielen $4\,€$ ausgezahlt werden.
Gib die Bedeutung des Terms $1-\left(\displaystyle \dfrac{35}{36}\right)^{10}$ im Sachzusammenhang an.

(6 BE)

$X$ : Betrag in $€$ , der an den Spieler ausgezahlt wird

Werte für $X$ bestimmen:

$1+1=2$
$1+2=3=2+1$
$2+2=4$

In diesem Spiel lassen sich aus den Zahlen $1$ und $2$ als Summe die Zahlen $2, 3$ und $4$ bilden.

Mögliches Ereignis angeben:

$A$ : ein gerader Betrag wird ausgezahlt

$\begin{array}[t]{rll} P(A)&=&P(X=2)+P(X=4) &\quad \\[5pt] &=&\dfrac{25}{36}+ \dfrac{1}{36}&\quad \\[5pt] &=&\dfrac{26}{36}&\quad \\[5pt] \end{array}$

Erwartungswert bestimmen:

Damit das Spiel fair ist, muss für den Erwartungswert $E(X)=3$ gelten, sodass sich die Einsätze und die Auszahlungen ausgleichen.

$\begin{array}[t]{rll} E(X)&=&2 \cdot \dfrac{25}{36}+ 3 \cdot \dfrac{10}{36}+ 4 \cdot \dfrac{1}{36} &\quad \\[5pt] &=&\dfrac{7}{3} \neq 3 \end{array}$

Der Erwartungswert beträgt $E(X)=\dfrac{7}{3} \neq 3$ und daher ist das Spiel nicht fair.

Neuen Zahlenwert $a$ berechnen:

Für den Erwartungswert muss $E(X)=5$ gelten, sodass das Spiel fair ist.
Werte die $X$ annehmen kann: $2$ , $1+a$ und $2a$

Daraus folgt eine neue Wahrscheinlichkeitsverteilung:

$k$	$P(X=k)$
$2$	$\dfrac{25}{36}$
$3$	$\dfrac{10}{36}$
$4$	$\dfrac{1}{36}$

$E(X)=5$

$a=10$

Vollständige Lösung anzeigen

Die "2"-Seitenfläche des Würfels muss mit dem Zahlenwert $a=10$ überklebt werden, damit das Spiel bei einem Einsatz von $5\,€$ fair ist.

Es wird $10$ -mal mit dem abgebildeten Würfel gespielt.

Wahrscheinlichkeit berechnen, dass bei mindestens zwei Spielen $4\,€$ ausgezahlt werden:

$4\,€$ werden ausgezahlt, wenn zweimal die $2$ gewürfelt wird.

$P(X=4)=\dfrac{1}{36}$

$n=10$ , $p=\dfrac{1}{36}$

Definiere eine neue Zufallsvariable $Y$ :
$Y$ : Anzahl der Spiele, in denen $4\,€$ ausgezahlt werden
$Y$ ist binomialverteilt mit $B_{10; \frac{1}{36}}$ .

$\begin{array}[t]{rll} P(Y\geq 2)&=&1- P(Y\leq 1) &\quad \\[5pt] \end{array}$

Die Wahrscheinlichkeit kann mit Hilfe eines GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ vars (distr) $\to$ B: binomcdf

$\blacktriangleright$ Casio fx-CG

Statistik: F5: DIST $\to$ F5: BINOM $\to$ F2: Bcd

$\begin{array}[t]{rll} P(Y\geq 2)&=&1- P(Y\leq 1) &\quad \\[5pt] &\approx&1- 0,97 &\quad \\[5pt] &=&0,03&\quad \\[5pt] \end{array}$

Mit einer Wahrscheinlichkeit von ca. $3\,\%$ wird bei mindestens zwei Spielen $4\,€$ ausgezahlt.

Bedeutung des Terms $1-\left(\dfrac{35}{36}\right)^{10}$ angeben:

Der Term beschreibt die Wahrscheinlichkeit dafür, dass bei $10$ Spielen mindestens bei einem Spiel $4\,€$ ausgezahlt werden.

$\begin{array}[t]{rll} P(Y\geq 1)&=&1- P(Y=0) &\quad \\[5pt] &=&1-\left(\dfrac{35}{36}\right)^{10}&\quad \\[5pt] \end{array}$