Aufgabe 1A

Eine Minigolfbahn enthält als Hindernis eine Welle. Die auf $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=0,5x^{4}-4x^{3}+11x^{2}-12x+4,5$ beschreibt für $1\leq x\leq 3$ modellhaft die Seitenansicht der Welle. Für $x\leq 1$ und $x\geq 3$ sind die Abschnitte der Bahn waagerecht und in der Seitenansicht durch die $x$ -Achse gegeben. Alle Angaben haben die Einheit Meter $(\text{m})$ .
Eine dreidimensionale Ansicht ist in Abbildung 1 dargestellt.

Grafische Darstellung einer Fläche mit einer Welle und einer kreisförmigen Basis im xy-Koordinatensystem.

Abb. 1

Bestimme die maximale Höhe der Bahn.
Untersuche, ob der Übergang zur Welle an der Stelle $x=1$ sprung- und knickfrei ist.
Die größte Steigung der Bahn soll den Wert $0,8$ nicht überschreiten.
Entscheide, ob die Minigolfbahn diese Bedingung erfüllt, und begründe deine Entscheidung.

(11 BE)

Der Ball wird modellhaft als punktförmig angenommen. Bei einem festen Schlag hebt er am Punkt $P (1,42\mid f(1,42))$ von der Bahn ab. Seine Flugbahn ab dem Punkt $\mathrm{P}$ kann näherungsweise durch die Parabel $q$ mit $q(x)=-0,28x^{2}+1,56x-1,42$ beschrieben werden.
Zeige, dass der Ball nicht direkt im Loch bei $x=5$ landet.
Berechne den Winkel, unter dem der Ball auf die Bahn trifft.
Bestimme den maximalen vertikalen Abstand des Balles von der Welle.

(11 BE)

Das Hindernis soll auf einer Seite verkleidet werden. Die Kosten der Verkleidung betragen pro Quadratmeter $40\,€$ .
Berechne die Kosten für die Seitenverkleidung. Die Seitenverkleidung soll so wie in Abbildung 2 dargestellt gestrichen werden. Der zur Mitte der Verkleidung symmetrische Farbstreifen soll $0,3\,\text{m}^{2}$ groß sein.

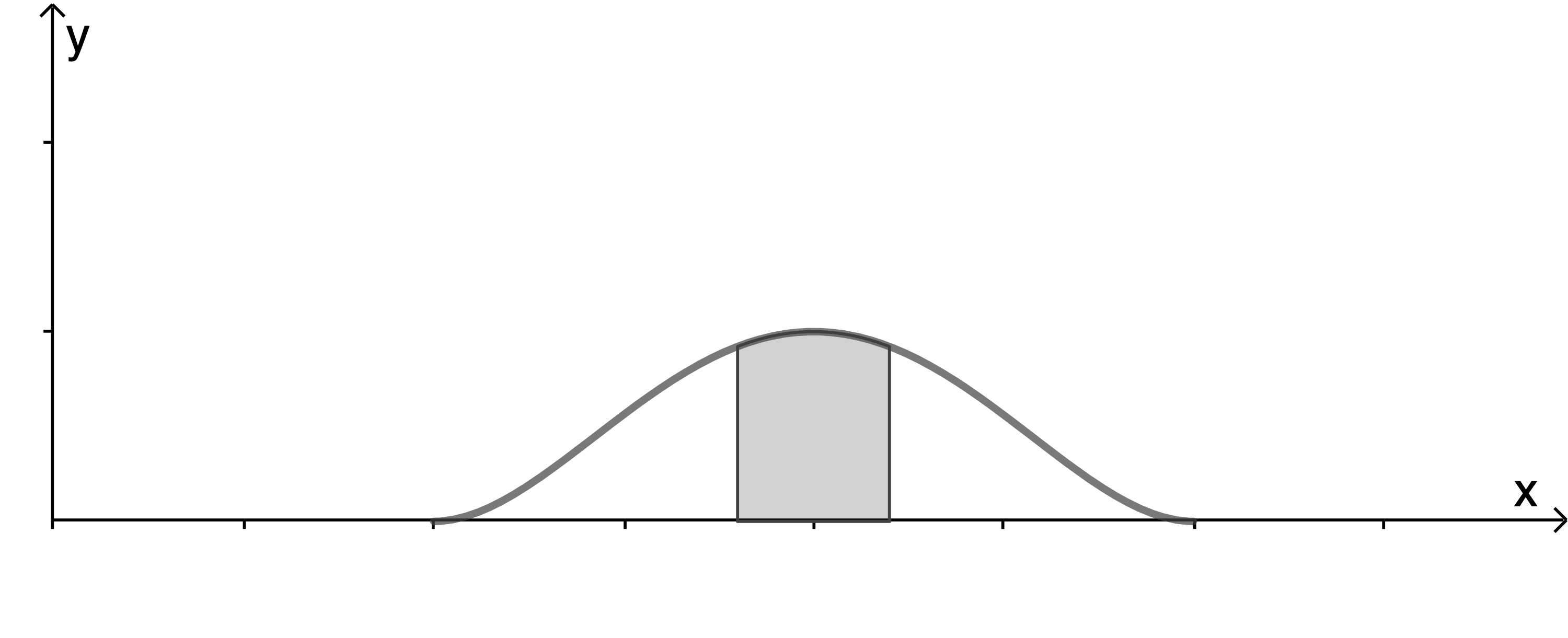
Grafik einer Funktion mit einem hervorgehobenen Bereich unter der Kurve. Achsen sind beschriftet.

Abb. 2

Erläutere, dass man die Breite dieses Streifens mithilfe der Gleichung $\displaystyle \int_{2}^{k} f(x)dx$ $=0,15$ berechnen kann.

(8 BE)

Unabhängig vom Sachzusammenhang gilt für eine nicht konstante ganzrationale Funktion $g$ :

Ihr Graph ist achsensymmetrisch zur Geraden mit $x=2.$
$\( g$

Entscheide, welchen Grad $g$ mindestens haben muss, und begründe deine Entscheidung.

(4 BE)

Maximale Höhe des Graphen der Funktion $f$ bestimmen:

Die maximale Höhe der Bahn entspricht dem Maximum von $f$ . Der Hochpunkt kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt des Graphen der Funktion $f$ befindet sich bei $H_f(2 \mid 0,5)$ .
Daraus folgt, dass die maximale Höhe der Bahn $0,5$ Meter beträgt.

Auf einen sprung-und knickfreien Übergang an der Stelle $x=1$ untersuchen:

Der Übergang des Graphen der Funktion $f$ und der x-Achse ist sprungfrei, wenn $f(1)=0$ gilt.

$f(1)=0$

Vollständige Lösung anzeigen

Daraus folgt, dass der Übergang sprungfrei ist.

Der Übergang des Graphen der Funktion $f$ und der x-Achse ist knickfrei, wenn $\(f$ gilt.
Die Ableitung von $f$ entspricht der Steigung des Graphen der Funktion in diesem Punkt.

$\(f$

Einsetzen von $x=1$ liefert: $\(f$

Daraus folgt, dass der Übergang knickfrei ist.

Der Übergang zur Welle an der Stelle $x=1$ ist sprung- und knickfrei.

Maximale Steigung des Graphen der Funktion $f$ ermitteln:

Die maximale Steigung des Graphen der Funktion $f$ entspricht dem Maximum der Funktion $f^{´}$ .
Der Hochpunkt des Graphen der Funktion $\(f$ kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt des Graphen von $\(f$ liegt bei $\(H_{f$ .
Daraus folgt, dass die maximale Steigung des Graphen der Funktion $f$ $\, m=0,77$ beträgt.

Die größte Steigung der Minigolfbahn ist $\leq 0,8$ und daher erfüllt die Minigolfbahn die Bedingung.

Nullstelle des Graphen der Funktion $q$ bestimmen:

Die Nullstelle des Graphen der Funktion $q$ kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 2: zero

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F1: ROOT

Die Nullstelle des Graphen von $q$ befindet sich bei $x\approx 4,43$ .
Der Ball kommt bei $x\approx 4,43$ auf der Bahn wieder auf und landet somit nicht direkt bei $x=5$ im Loch.

alternativer Lösungsweg:

$q(5)$ bestimmen:

Der Ball würde bei $x=5$ direkt im Loch landen, falls $q(5)=0$ gilt.

$q(5)=-0,62\neq0$

Vollständige Lösung anzeigen

Daraus folgt, dass der Ball nicht direkt im Loch bei $x=5$ landet.

Steigungswinkel des Graphen von $q$ und der x-Achse berechnen:

Es gilt: $m=\tan(\alpha)$ und $\alpha=\tan^{-1}(m)$

$q^´(x)=-0,56x+1,56$

Bestimme den Funktionswert für $x=4,43$ (Nullstelle des Graphen der Funktion $q$ ).
$\(q$

Das Einsetzen in obige Formel liefert: $\alpha=\tan^{-1}(0,92)\approx42,56^{\circ}$
Der Ball trifft ungefähr unter einem Winkel von $42,56^{\circ}$ auf die Bahn.

Maximaler vertikaler Abstand der Graphen der Funktionen $f$ und $q$ bestimmen:

Definiere eine neue Funktion $d$ mit $d(x)=q(x)-f(x)$
Der maximale vertikale Abstand der Graphen der Funktionen $f$ und $q$ entspricht dem Maximum der Funktion $d$ .
Der Hochpunkt des Graphen der Funktion $d$ kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt des Graphen von $d$ liegt bei $H_d(2,97 \mid 0,74)$ .
Daraus folgt, dass der maximale vertikale Abstand des Balles und der Welle $0,74$ Meter beträgt.

Kosten für die Seitenverkleidung berechnen:

Ein Quadratmeter der Verkleidung kostet $40\,€$ .
Das Integral $A=\displaystyle\int_{1}^{3}f(x) \,\mathrm dx$ beschreibt den Flächeninhalt des Hindernisses.
Das Integral kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

$A=\displaystyle\int_{1}^{3}f(x) \,\mathrm dx\approx0,53$

Kosten für die Seitenverkleidung: $0,53 \cdot 40\,€=21,20\,€$

Die Kosten für die Seitenverkleidung betragen $21,20\,€$ .

Ausdruck $\displaystyle\int_{2}^{k}f(x)\;\mathrm dx = 0,15$ erläutern:

Der Graph der Funktion $f$ hat an der Stelle $x=2$ einen Hochpunkt.
Der Farbstreifen ist symmetrisch zur Geraden mit der Gleichung $x=2$ . Daraus folgt, dass die Flächenstücke links und rechts der Geraden $x=2$ gleich groß sind und einen Flächeninhalt von $0,15 \,\text{m}^2$ haben.
Das angegebene Integral beschreibt den Flächeninhalt des rechten Flächenstücks von $x=2$ (Mitte des Streifens) bis $x=k$ (rechte Begrenzung). Der Abstand von $k$ zur Stelle $2$ entspricht der halben Breite des Streifens.
Da der Farbstreifen symmetrisch ist, wird die gesamte Breite des Streifens mit $b=2\cdot (k-2)\,[\text{m}]$ beschrieben.
Daraus folgt, dass die Breite des Streifens mit Hilfe der Gleichung $\displaystyle\int_{2}^{k}f(x)\;\mathrm dx = 0,15$ berechnet werden kann.

Minimalen Grad der Funktion $g$ bestimmen:

Die Funktion $g$ muss an der Stelle $x=2$ eine Extremstelle haben, sodass der Graph von $g$ achsensymmetrisch zur Geraden $x=2$ ist. Außerdem folgt aus der Achsensymmetrie, dass $\(g$ gelten muss.
Aufgrund der Achsensymmetrie zur Geraden mit $x=2$ und $g^{´}(1)=0$ gilt $g^{´}(2)=0$ sowie $g^{´}(1)=g^{´}(3)=0$ .
Daraus folgt, dass der Graph der Funktion $g^´$ mindestens drei Nullstellen besitzt.
Die Funktion $g$ muss also mindestens Grad $4$ haben, um die beiden Bedingungen zu erfüllen.