Aufgabe 1B
Aufgabe 1B
Gegeben ist die Funktion
a)
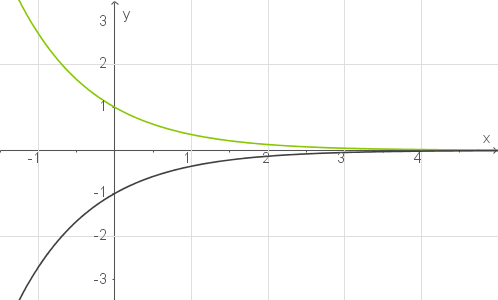
Die Abbildung 1 zeigt die Graphen der Funktionen  und
und  .
Entscheide, welche der Funktionen zu welchem Graphen gehört.
Begründe, dass der Graph von
.
Entscheide, welche der Funktionen zu welchem Graphen gehört.
Begründe, dass der Graph von  keinen Extrempunkt hat.
Berechne die Koordinaten des Punktes
keinen Extrempunkt hat.
Berechne die Koordinaten des Punktes  , in dem die Tangente an den Graphen von
, in dem die Tangente an den Graphen von  die Steigung
die Steigung  hat.
Die Koordinatenachsen, der Graph der Funktion
hat.
Die Koordinatenachsen, der Graph der Funktion  und die Gerade zu
und die Gerade zu  mit
mit  schließen eine Fläche ein.
Berechne einen Wert für
schließen eine Fläche ein.
Berechne einen Wert für  so, dass der Inhalt dieser Fläche
so, dass der Inhalt dieser Fläche  Flächeneinheiten beträgt. Ohne Nachweis kannst du verwenden, dass
Flächeneinheiten beträgt. Ohne Nachweis kannst du verwenden, dass  mit
mit  eine Stammfunktion zu
eine Stammfunktion zu  ist.
ist.
(11P)
b)
Für eine Stelle  sind
sind  ,
,  und
und  die Eckpunkte eines rechtwinkligen Dreiecks. Es gibt einen Punkt
die Eckpunkte eines rechtwinkligen Dreiecks. Es gibt einen Punkt  auf dem Graphen von
auf dem Graphen von  so, dass der Flächeninhalt des Dreiecks maximal ist.
Bestimme die Koordinaten der Punkte
so, dass der Flächeninhalt des Dreiecks maximal ist.
Bestimme die Koordinaten der Punkte  und
und  .
Betrachtet werden alle Punkte, die auf dem Graphen von
.
Betrachtet werden alle Punkte, die auf dem Graphen von  liegen.
Bestimme die Koordinaten des Punktes
liegen.
Bestimme die Koordinaten des Punktes  , der vom Ursprung den kleinsten Abstand hat.
Die Gerade
, der vom Ursprung den kleinsten Abstand hat.
Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  und ist senkrecht zur Tangente an den Graphen von
und ist senkrecht zur Tangente an den Graphen von  im Punkt
im Punkt  .
Untersuche, ob
.
Untersuche, ob  eine Ursprungsgerade ist. Ohne Nachweis kannst du verwenden: Wenn für die Steigungen
eine Ursprungsgerade ist. Ohne Nachweis kannst du verwenden: Wenn für die Steigungen  und
und  zweier Geraden die Beziehung gilt:
zweier Geraden die Beziehung gilt:  , dann stehen die zugehörigen Geraden senkrecht aufeinander.
, dann stehen die zugehörigen Geraden senkrecht aufeinander.
(13P)
c)
Gegeben sind die Funktion  mit
mit  ,
,  und ihre Ableitungsfunktion
und ihre Ableitungsfunktion  mit
mit  .
Die Graphen von
.
Die Graphen von  und
und  schneiden sich im Punkt
schneiden sich im Punkt  .
Die Graphen von
.
Die Graphen von  und
und  und die
und die  -Achse schließen für
-Achse schließen für  eine Fläche ein.
Bestimme deren Inhalt.
Beurteile mithilfe der Ableitungen von
eine Fläche ein.
Bestimme deren Inhalt.
Beurteile mithilfe der Ableitungen von  und
und  die Behauptung, dass für
die Behauptung, dass für  weitere Schnittpunkte existieren können.
Untersuche mithilfe des Graphen der Funktion
weitere Schnittpunkte existieren können.
Untersuche mithilfe des Graphen der Funktion  , für welche Stellen die zugehörigen Funktionswerte von
, für welche Stellen die zugehörigen Funktionswerte von  nur einmal auftreten.
nur einmal auftreten.
Bildnachweise [nach oben]
(10P)
© 2016 - SchulLV.
a)
b)
Die Punkte  ,
,  und
und  bilden ein rechtwinkliges Dreieck.
Du sollst den Parameter
bilden ein rechtwinkliges Dreieck.
Du sollst den Parameter  so bestimmen, dass der Flächeninhalt des Dreiecks maximal wird. Dazu bestimmst du zunächst den Flächeninhalt als Funktion von
so bestimmen, dass der Flächeninhalt des Dreiecks maximal wird. Dazu bestimmst du zunächst den Flächeninhalt als Funktion von  .
.
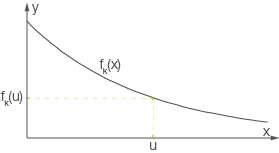 Abb. 1: Skizze des Dreiecks
Abb. 1: Skizze des Dreiecks
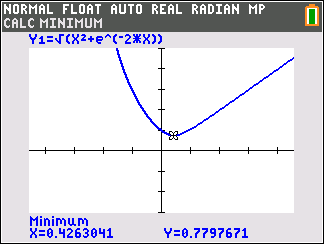 Abb. 2: Minimum der Abstandsfunktion
Abb. 2: Minimum der Abstandsfunktion
c)
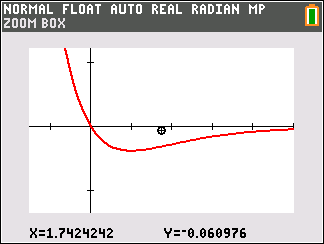
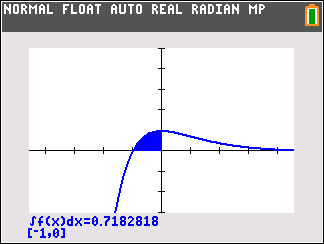 Abb. 3: Integral graphisch berechnen
Abb. 3: Integral graphisch berechnen
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.