Pflichtteil 2

Aufgabe P1

Eine Funktion $f$ ist gegeben durch $f(x)=x^2-6x, \; x \in \mathbb{R}.$

Gib die Koordinaten des Scheitelpunktes an.

(2 BE)

Bestimme eine Gleichung der Tangente an den Graphen von $f$ im Punkt $P(-2 \mid f(-2)).$

(3 BE)

Aufgabe P2

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x) = x^3-x.$

Einer der folgenden Graphen I, II und III stellt $f$ dar. Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.

Graph einer mathematischen Funktion mit den Achsen x und y.

Graf einer mathematischen Funktion mit x- und y-Achse, zeigt eine grüne Kurve.

Graph einer Funktion mit x- und y-Achse, zeigt eine steigende Kurve.

(2 BE)

Berechne den Inhalt der Fläche, die der Graph von $f$ und die $x$ -Achse einschließen.

(3 BE)

Aufgabe P3

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x) = \mathrm{e}^x + 1.$

Bestimme: $\displaystyle\int_{0}^{1}f(x)\;\mathrm dx.$

(3 BE)

Der Graph der Funktion $g$ kann aus dem Graphen von $f$ durch Spiegeln an der $y$ -Achse und Verschieben um $3$ in positive $y$ -Richtung erzeugt werden.
Gib einen Funktionsterm von $g$ an.

(2 BE)

Aufgabe P4

Von den Personen, die einen bestimmten Allergietest machen, haben 15 $\,\%$ Heuschnupfen. Der Test ist bei einer Person, die Heuschnupfen hat, mit einer Wahrscheinlichkeit von 90 $\,\%$ positiv. Die Wahrscheinlichkeit dafür, dass der Test bei einer Person positiv ist, obwohl diese Person keinen Heuschnupfen hat, beträgt 2 $\,\%.$

Von den Personen, die den Test machen lassen, wird eine Person zufällig ausgewählt.
Berechne die Wahrscheinlichkeit dafür, dass diese Person keinen Heuschnupfen hat und der Test positiv ist.

(2 BE)

Deute den Term $\dfrac{0,15 \cdot 0,9}{0,15 \cdot 0,9 + 0,85 \cdot 0,02}$ im Sachzusammenhang.

(3 BE)

Aufgabe P5

Die Zufallsgröße $X$ ist binomialverteilt; die Trefferwahrscheinlichkeit beträgt $p = \frac{1}{4}.$
Vervollständige die folgende Gleichung zur Berechnung einer Wahrscheinlichkeit:

$P(X= \;\;\;) = \pmatrix{\\3} \cdot \left( \dfrac{1}{4} \right)^3 \cdot \left(\dfrac{}{} \right)^2$

(2 BE)

Die Abbildung zeigt die symmetrische Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $Y.$

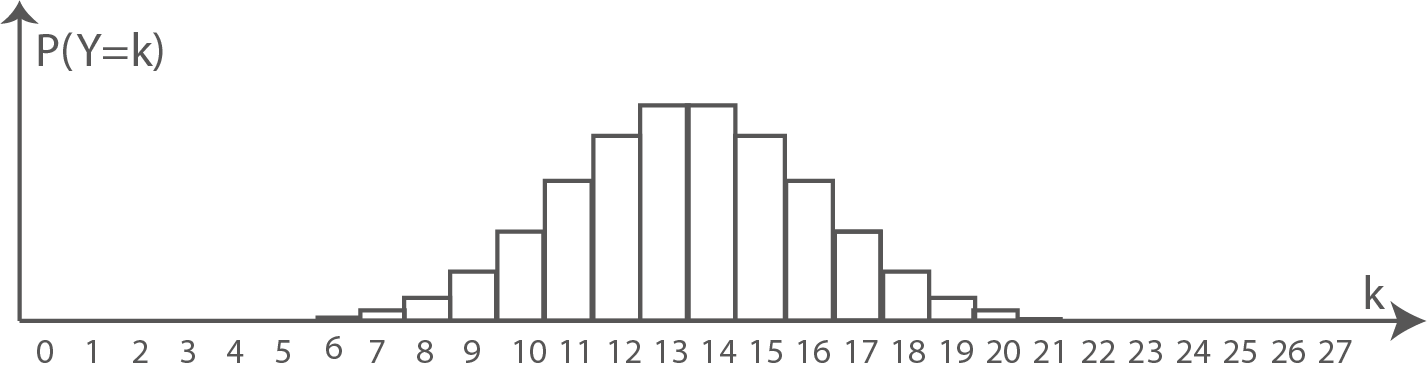Histogramm zur Darstellung von Wahrscheinlichkeiten für Werte k.

Gegeben sind die Wahrscheinlichkeitswerte $P (Y \leq 15) \approx 0,78$ und $P (Y = 12) \approx 0,13$ .
Berechne unter Verwendung dieser Werte einen Näherungswert für die Wahrscheinlichkeit $P(Y = 14).$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung P1

$\(f$
$\(f$

$2x -6 = 0$
$x=3$

$f(3)= 3^2 - 6 \cdot 3 = -9$

Der Scheitelpunkt hat die Koordinaten $(3 \mid -9).$

Die allgemeine Tangentengleichung lautet $y=mx+b.$

$f(-2)=(-2)^2-6 \cdot (-2)=16$

$\(m=f$

Die Koordinaten von Punkt P in die Tangentengleichung eingesetzt, ergeben $16=-10 \cdot (-2) +b$ $=20+b.$
Damit ist $b=-4$ und somit $y = -10x -4.$

Lösung P2

Graph II kommt nicht in Frage, da $x^3 \leq x$ für $x \in [0;1]$ und somit im gegebenen Intervall $x^3-x \leq 0$ . Im Intervall $[0,1]$ liegt der Graph II jedoch über der $x$ -Achse.

Graph III kommt nicht infrage, da die Steigung des Graphen von $f$ für $-0,5 \leq x \leq 0,5$ nicht konstant ist.

Die Fläche, die der Graph von $f$ und die $x$ -Achse einschließen, liegt im Intervall $[-1,1].$ Da der Graph der Funktion punktsymmetrisch zum Ursprung ist, wird der Flächeninhalt der Fläche wie folgt berechnet:

$2\displaystyle\int_{-1}^{0} (x^3 -x)\;\mathrm dx$ $= 2 \left[\dfrac{1}{4}x^4 - \dfrac{1}{2} x^2 \right]_{-1}^0$ $= -2\left(\dfrac{1}{4}-\dfrac{1}{2}\right) = \dfrac{1}{2}$

Lösung P3

$\displaystyle\int_{0}^{1}\mathrm{e}^x+1\;\mathrm dx= \left[\mathrm{e}^x + x\right]_0^1$ $= \mathrm{e}+1-(1+0)=\mathrm{e}$

$g(x) = \mathrm{e}^{-x}+4$

Lösung P4

Vollständigen Rechenweg anzeigen

$1,7\%$

Der Term gibt die Wahrscheinlichkeit dafür an, dass eine Person, die aus der Gruppe der Personen mit positivem Test zufällig ausgewählt wird, tatsächlich Heuschnupfen hat.

Lösung P5

$P(X=3)=\pmatrix{5\\3} \cdot \left(\dfrac{1}{4}\right)^3 \cdot \left(\dfrac{3}{4}\right)^2$

Aus dem Schaubild ist ersichtlich, dass $P(Y=12)=P(Y=15)$ gilt, wobei beide Wahrscheinlichkeiten nach dem Hinweis ungefähr den Wert $0,13$ haben.

Weiter wird $P(Y \leq 13)=P(Y \geq 14) = 0,5$ abgelesen.

Vollständigen Rechenweg anzeigen

$P(X=14)=0,0015$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?