Pflichtteil
Aufgabe P1
Gegeben ist die auf
a)
Berechne die Nullstelle von 
(2 BE)
b)
Bestimme eine Gleichung der Tangente an den Graphen von  im Schnittpunkt mit der
im Schnittpunkt mit der  -Achse.
-Achse.
(3 BE)
Aufgabe P2
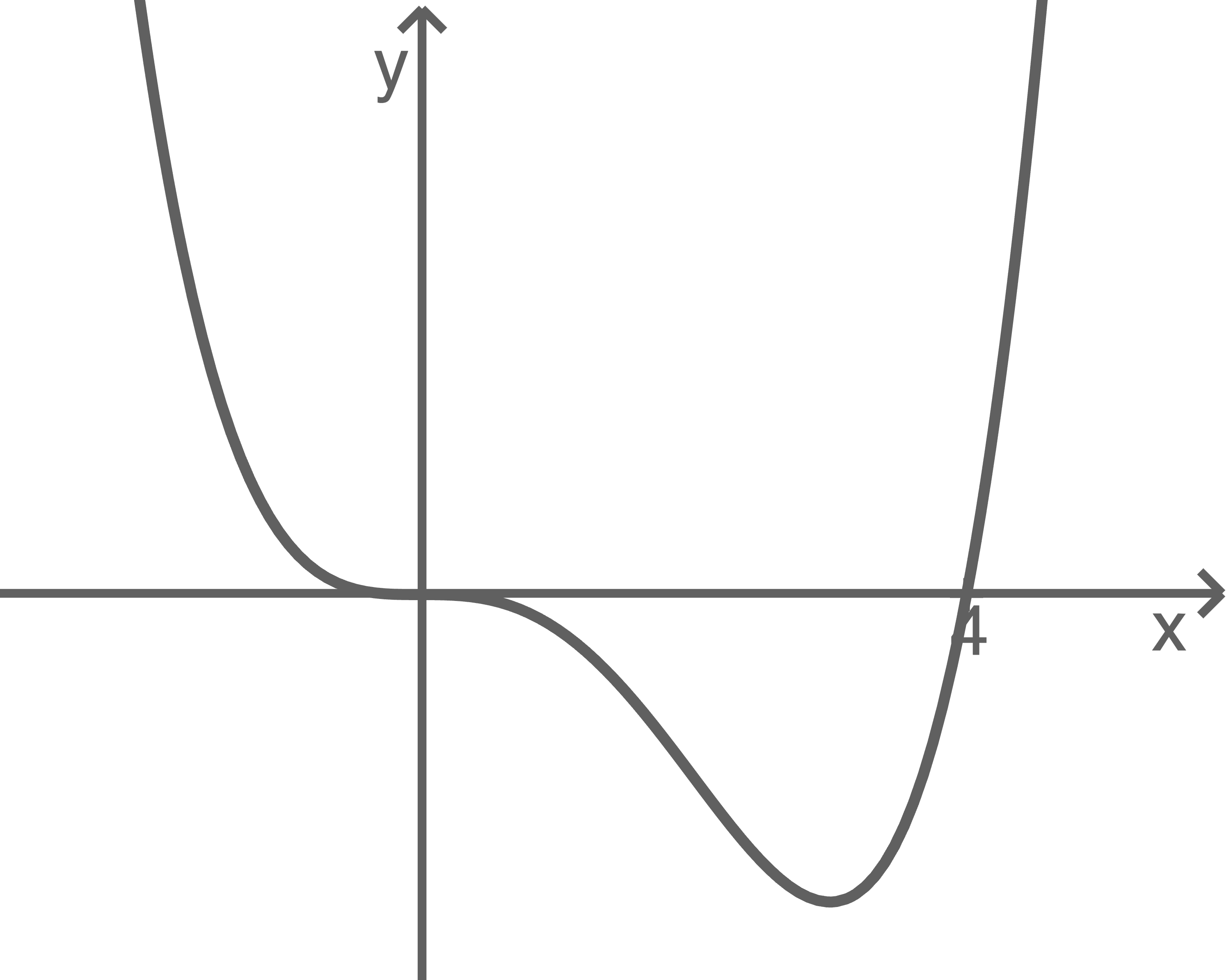
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion  mit
mit 
a)
Berechne den Wert des Integrals 
(2 BE)
b)
Beurteile, ob die folgende Aussage richtig ist:
Für die Abbildung wurde eine Längeneinheit auf der  -Achse ebenso groß gewählt wie auf der
-Achse ebenso groß gewählt wie auf der  -Achse.
-Achse.
(3 BE)
Aufgabe P3
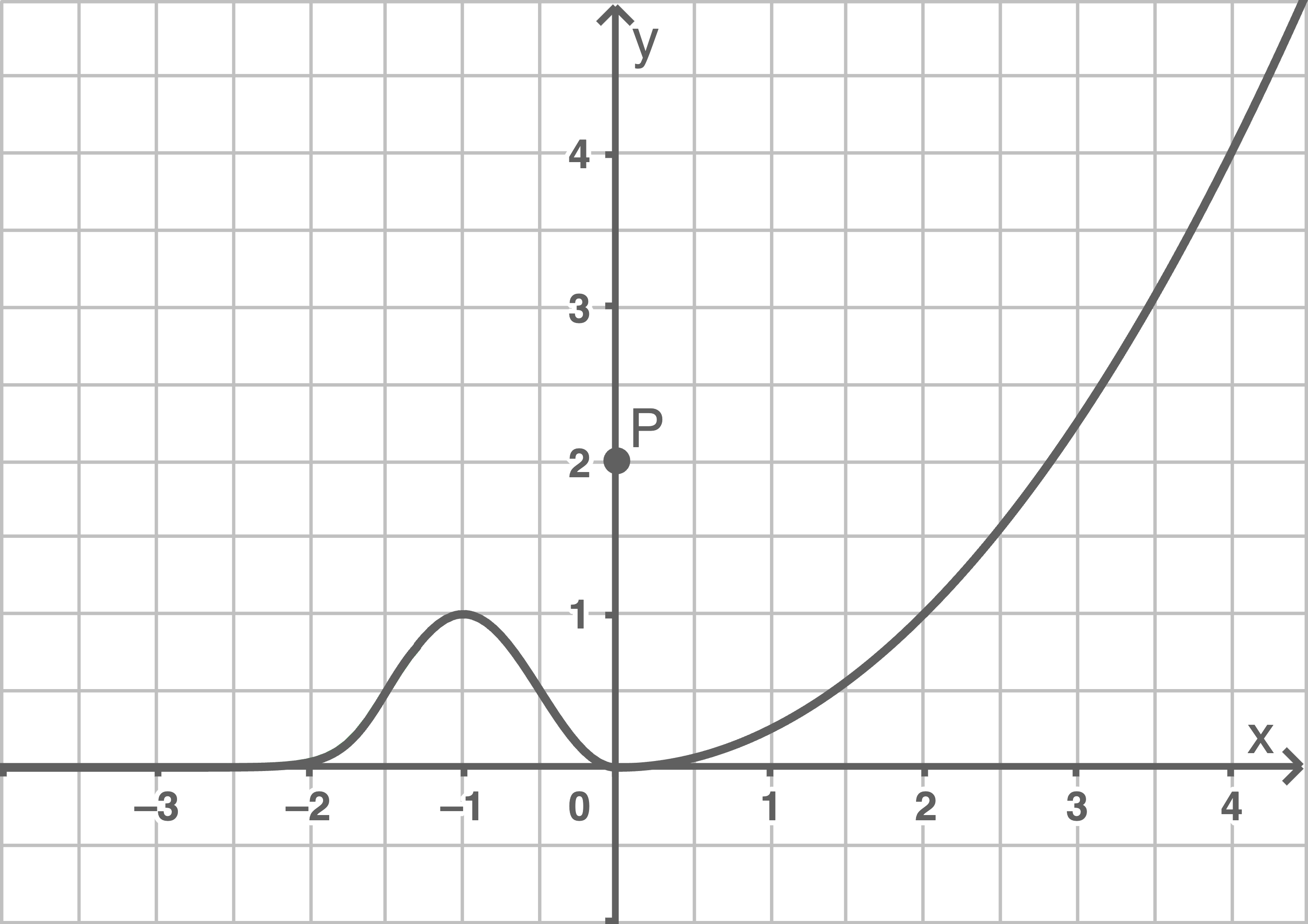
Die Abbildung zeigt den Punkt  und den Graphen der in
und den Graphen der in  definierten Funktion
definierten Funktion  Der Graph von
Der Graph von  hat die einzigen Extrempunkte
hat die einzigen Extrempunkte  und
und 
a)
Gegeben ist die Funktion  mit
mit  Gib die Koordinaten des Hochpunkts des Graphen von
Gib die Koordinaten des Hochpunkts des Graphen von  an.
an.
(2 BE)
b)
Der Graph einer Stammfunktion von  verläuft durch den Punkt
verläuft durch den Punkt  Skizziere diesen Graphen in der Abbildung.
Skizziere diesen Graphen in der Abbildung.
(3 BE)
Aufgabe P4
Bei einem Spielautomaten gewinnt man in
a)
Es werden 10 Spiele gespielt. Die Anzahl der gewonnenen Spiele ist binomialverteilt.
Gib einen Term an, mit dem die Wahrscheinlichkeit für das folgende Ereignis berechnet werden kann:
Es werden mindestens 2, aber weniger als 4 Spiele gewonnen.
(3 BE)
b)
Der Einsatz für ein Spiel beträgt  Gewinnt man ein Spiel, so werden
Gewinnt man ein Spiel, so werden  ausgezahlt.
Berechne den auf lange Sicht zu erwartenden Gewinn pro Spiel.
ausgezahlt.
Berechne den auf lange Sicht zu erwartenden Gewinn pro Spiel.
(2 BE)
Aufgabe P5
Gegeben sind die Gerade
a)
Begründe, dass  nicht auf
nicht auf  liegt.
liegt.
(1 BE)
b)
Gib eine Gleichung der Ebene an, die  und
und  enthält.
enthält.
(2 BE)
c)
Bestimme den Wert für  so, dass
so, dass  und
und  parallel zueinander sind.
parallel zueinander sind.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung P1
a)
Es soll gelten:
![\(\begin{array}[t]{rll}
f(x)&=& 0& \\[5pt]
2\mathrm e^x-4&=& 0 &\quad \scriptsize \mid\;+4 \\[5pt]
2\mathrm e^x &=& 4 &\quad \scriptsize \mid\; :2\\[5pt]
\mathrm e^x &=& 2 &\quad \scriptsize \mid\; \ln(\,)\\[5pt]
x&=& \ln(2)
\end{array}\)](https://mathjax.schullv.de/3563377d1f0e91cf8102a8771901b4af525b1e1edd3af6ae0c3e1185feef6650?color=5a5a5a)
b)
1. Schritt: Koordinaten des Schnittpunkts bestimmen
Der Graph von  schneidet die
schneidet die  -Achse an der Stelle
-Achse an der Stelle 
 -Koordinate berechnen:
-Koordinate berechnen:
 Die Koordinaten des Schnittpunkts sind somit gegeben durch
Die Koordinaten des Schnittpunkts sind somit gegeben durch  2. Schritt: Steigung
2. Schritt: Steigung  berechnen
Ableitung bestimmen:
berechnen
Ableitung bestimmen:
 An der Stelle
An der Stelle  gilt also:
gilt also:
 3. Schritt: Tangentengleichung aufstellen
Einsetzen der Koordinaten von
3. Schritt: Tangentengleichung aufstellen
Einsetzen der Koordinaten von  sowie der Steigung
sowie der Steigung  in die allgemeine Tangentengleichung liefert:
in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
y&=& m\cdot x+c& \\[5pt]
-2&=& 2\cdot 0+c& \\[5pt]
-2&=& c
\end{array}\)](https://mathjax.schullv.de/a89fdc437bf49df43e0e1913b0bb004d4ed997e750167c9aad8add766fc52920?color=5a5a5a) Eine Gleichung der Tangente folgt also mit:
Eine Gleichung der Tangente folgt also mit:

Lösung P2
a)
b)
Lösung P3
a)
Der Graph von  ergibt sich aus dem Graphen von
ergibt sich aus dem Graphen von  durch Verschiebung um 3 Längeneinheiten in positive
durch Verschiebung um 3 Längeneinheiten in positive  -Richtung und Streckung um den Faktor 2.
Der Hochpunkt des Graphen von
-Richtung und Streckung um den Faktor 2.
Der Hochpunkt des Graphen von  ist gegeben durch
ist gegeben durch  Aufgrund der Verschiebung entlang der
Aufgrund der Verschiebung entlang der  -Achse gilt für die
-Achse gilt für die  -Koordinate des Hochpunkts des Graphen von
-Koordinate des Hochpunkts des Graphen von  :
:
 Die
Die  -Koordinate folgt wegen der Streckung um den Faktor 2 mit:
-Koordinate folgt wegen der Streckung um den Faktor 2 mit:
 Die Koordinaten des Hochpunkts des Graphen von
Die Koordinaten des Hochpunkts des Graphen von  ergeben sich also zu
ergeben sich also zu 
b)
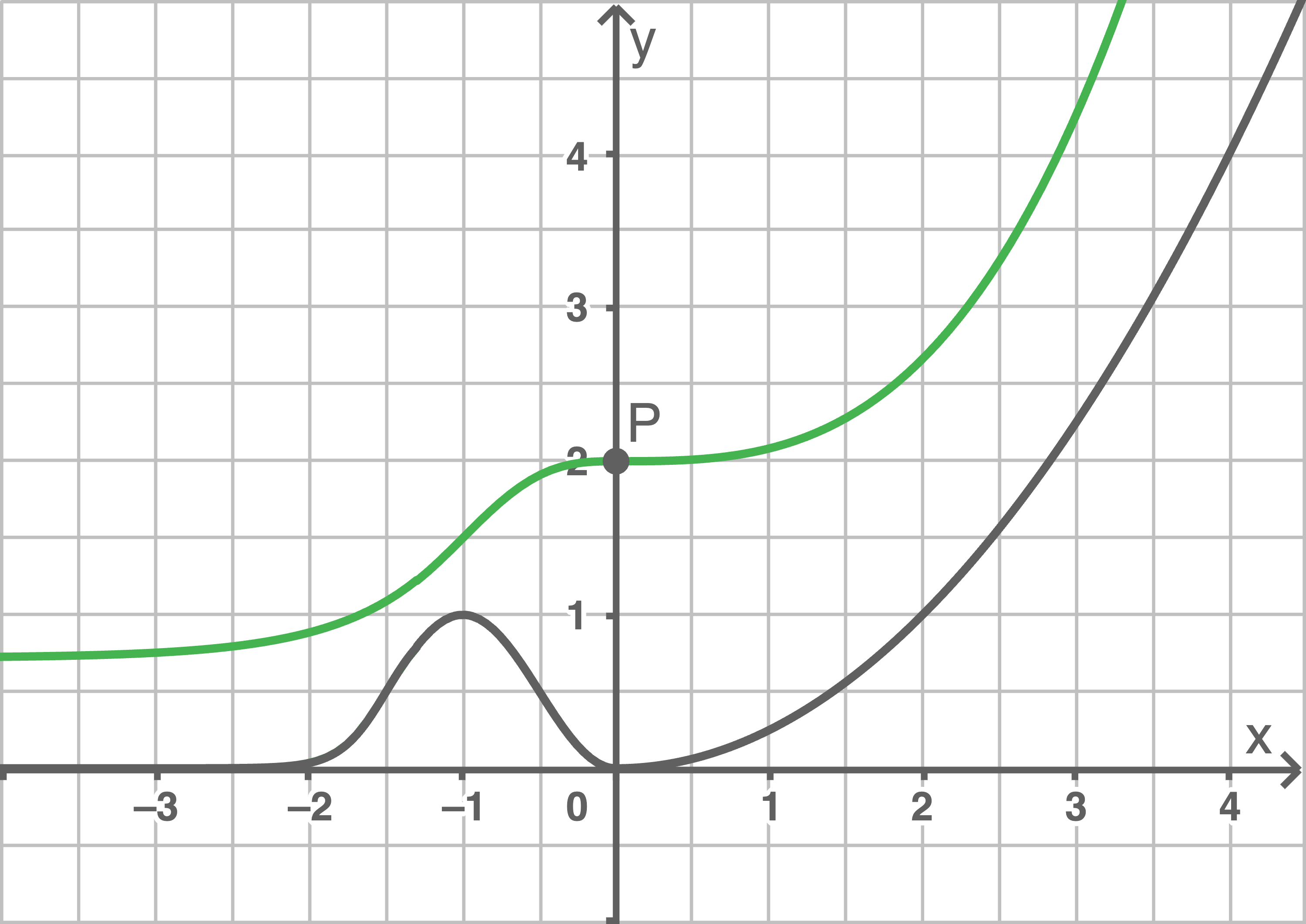
Lösung P4
a)
b)
Der zu erwartende Gewinn ergibt sich durch:

Lösung P5
a)
Aus der Geradengleichung von  folgt, dass alle Punkte von
folgt, dass alle Punkte von  die
die  -Koordinate
-Koordinate  besitzen.
Da
besitzen.
Da  jedoch die
jedoch die  -Koordinate 0 hat, liegt
-Koordinate 0 hat, liegt  folglich nicht auf
folglich nicht auf 
b)
c)
Ein Richtungsvektor der Gerade  ist gegeben durch:
ist gegeben durch:
 Da
Da  und
und  parallel sein sollen, muss es ein
parallel sein sollen, muss es ein  geben, sodass gilt:
geben, sodass gilt:
 Aus der ersten Zeile folgt:
Aus der ersten Zeile folgt:  Mit
Mit  folgt dann aus der dritten Zeile
folgt dann aus der dritten Zeile  Für
Für  sind die Geraden parallel.
sind die Geraden parallel.