Wahlaufgaben 1
Aufgabe Q1
Die Abbildung zeigt den Graphen 
einer in 
definierten Funktion 
.
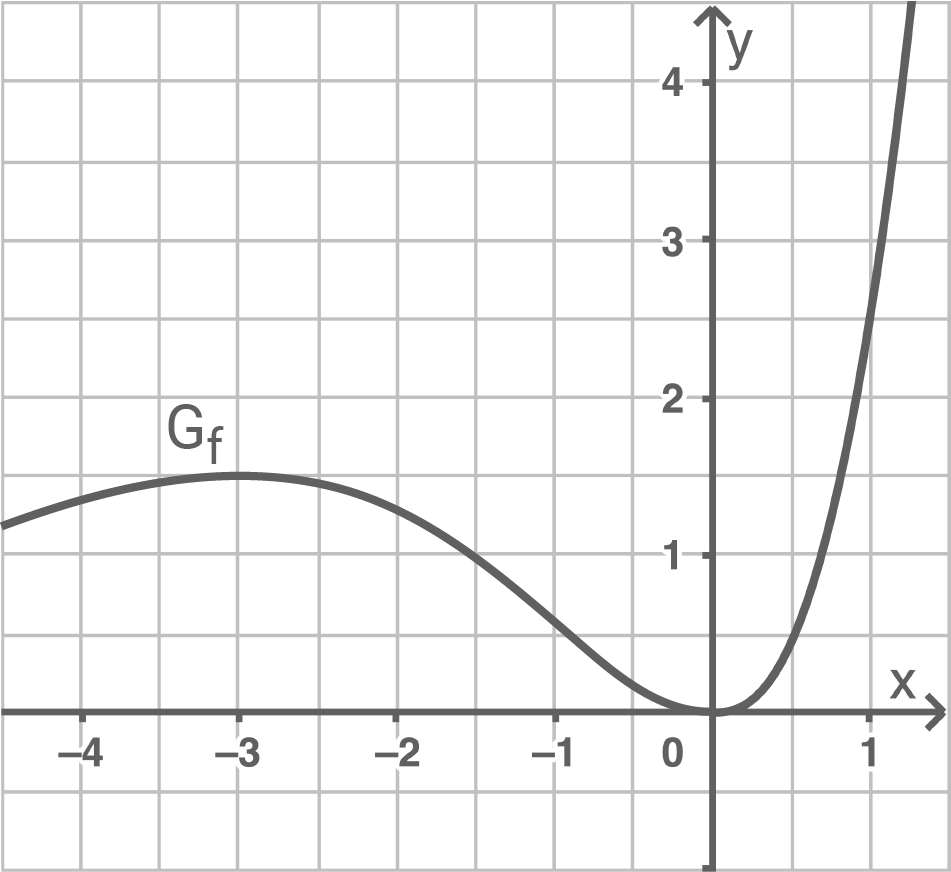
a)
Bestimme grafisch den Wert des Integrals 
(2 BE)
b)
Beschreibe, wie der Graph der in definierten Funktion 
mit 
aus erzeugt werden kann.
Gib die Koordinaten des Hochpunkts des Graphen von an.
(3 BE)
Aufgabe Q2
Im hinteren Teil eines Klassenzimmers stehen sechs Stühle in einer Reihe.
a)
Es gibt vier Möglichkeiten, drei der sechs Stühle so auszuwählen, dass zwischen je zwei ausgewählten Stühlen mindestens ein weiterer Stuhl steht.
Gib diese Möglichkeiten an.
(3 BE)
b)
Die Schüler Aaron, Bert und Can sollen sich so auf jeweils einen der sechs Stühle setzen, dass zwischen je zwei Schülern mindestens ein weiterer Stuhl steht.
Berechne, wie viele Möglichkeiten es dafür gibt.
(2 BE)
Aufgabe Q3
Gegeben sind die Punkte
a)
Entscheide, ob es einen Wert von 
gibt, für den die Gerade 
parallel zur 
-Ebene verläuft.
Begründe deine Entscheidung.
(2 BE)
b)
Der Koordinatenursprung und die Punkte 
und 
bilden ein Dreieck.
Ermittle diejenigen Werte von , für die das Dreieck in einen rechten Winkel hat.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung Q1
a)
Der Wert des Integrals gibt den Inhalt der Fläche zwischen dem Graphen und der 
-Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa ![\(8\cdot0,5^2=2\;[\text{FE}].\)](https://mathjax.schullv.de/f52af0e22124d1ded4d66412fc64dfb022b2971fc07ebf226bf4f3e0663bc090?color=5a5a5a)
b)
Der Graph der Funktion geht durch Spiegelung an der -Achse und Verschiebung um 2 Einheiten in positive 
-Richtung aus dem Graphen hervor.
Aus der Abbildung können die Koordinaten des Tiefpunkts von mit 
abgelesen werden.
Da der Graph und somit auch sein Hochpunkt und Tiefpunkt an der -Achse gespiegelt wird, entspricht der Tiefpunkt des Graphen von dem Hochpunkt des Graphen von vor der Verschiebung in -Richtung.
Verschieben um 2 Einheiten in positive -Richtung liefert dann:
Lösung Q2
a)
Eine Menge 
mit Zahlen 
, die die Positionen der ausgewählten Stühle in einer Reihe angibt, beschreibt eine mögliche Auswahl von drei Stühlen. Mit dieser Schreibweise ergeben sich die gesuchten Möglichkeiten wie folgt:
b)
Bei allen vier Möglichkeiten hat der erste Schüler drei Stühle zur Auswahl, der zweite Schüler zwei und der letzte nur noch einen Stuhl. Somit folgt für die gesuchte Anzahl an Möglichkeiten:
Lösung Q3
a)
Da die Punkte und unabhängig von immer unterschiedliche 
-Koordinaten haben, gibt es keinen solchen Wert für 
b)