Pflichtteil 1
Aufgabe P1
Eine Funktion
a)
Gib die Koordinaten des Scheitelpunktes an.
(2 BE)
b)
Bestimme eine Gleichung der Tangente an den Graphen von  im Punkt
im Punkt 
(3 BE)
Aufgabe P2
Gegeben ist die in
a)
Einer der folgenden Graphen I, II und III stellt  dar. Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.
dar. Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.






(2 BE)
b)
Berechne den Inhalt der Fläche, die der Graph von  und die
und die  -Achse einschließen.
-Achse einschließen.
(3 BE)
Aufgabe P3
Gegeben ist die in
a)
Bestimme: 
(3 BE)
b)
Der Graph der Funktion  kann aus dem Graphen von
kann aus dem Graphen von  durch Spiegeln an der
durch Spiegeln an der  -Achse und Verschieben um
-Achse und Verschieben um  in positive
in positive  -Richtung erzeugt werden.
-Richtung erzeugt werden.
Gib einen Funktionsterm von an.
an.
Gib einen Funktionsterm von
(2 BE)
Aufgabe P4
Gegeben sind die Punkte
a)
Bestimme denjenigen Wert von  , für den
, für den  und
und  den Abstand
den Abstand  haben.
haben.
(3 BE)
b)
Ermittle denjenigen Wert von  , für den das Dreieck
, für den das Dreieck  im Punkt
im Punkt  rechtwinklig ist.
rechtwinklig ist.
(2 BE)
Aufgabe P5
Die Abbildung zeigt einen Quader sowie die Ortsvektoren der Eckpunkte  und
und  . Die Grundfläche
. Die Grundfläche  ist quadratisch.
ist quadratisch.
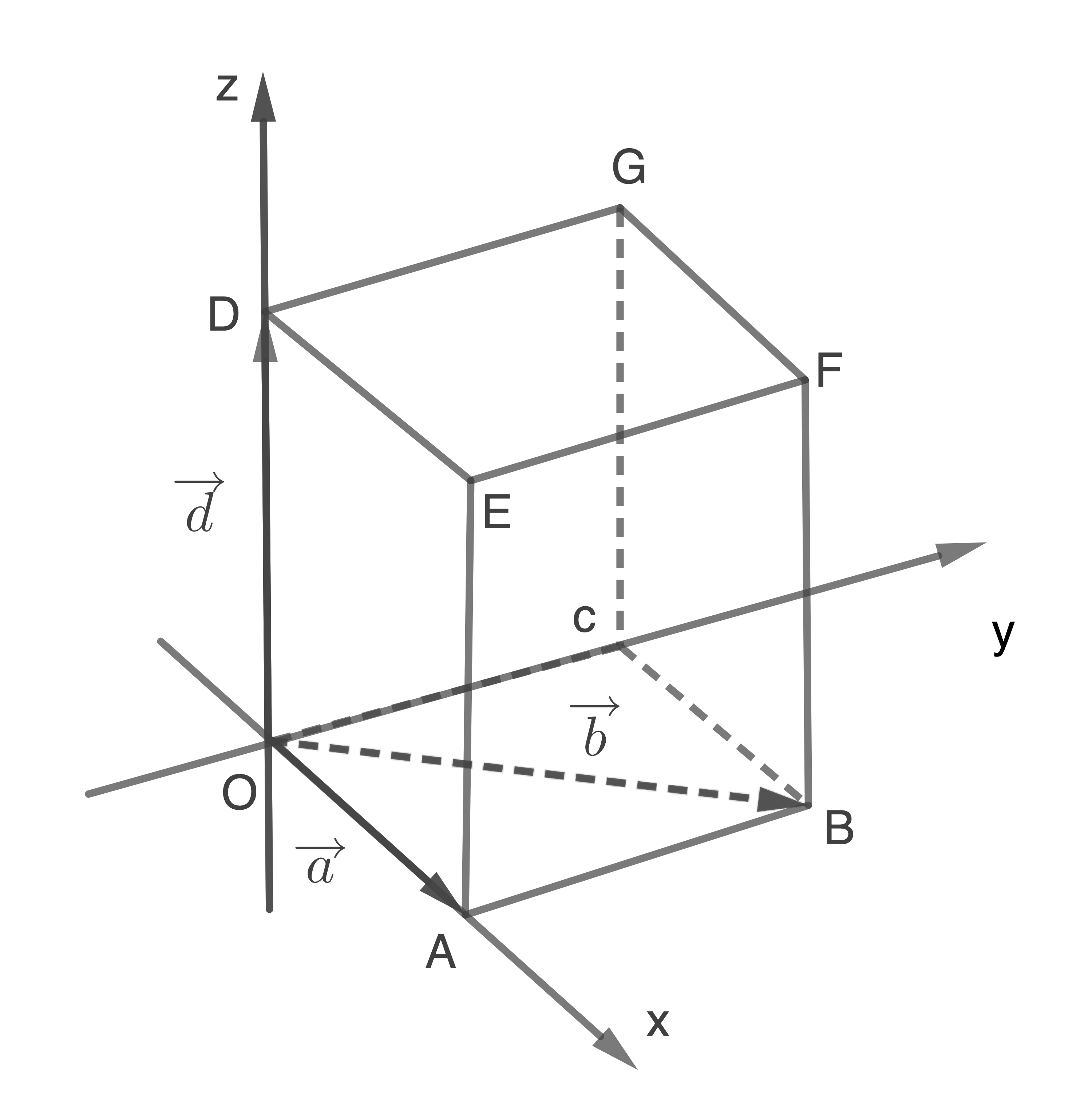
a)
Beschreibe die Lage des Punkts, zu dem der Ortsvektor  gehört.
gehört.
(1 BE)
Der Punkt
b)
Zeichne  in die Abbildung ein.
in die Abbildung ein.
(1 BE)
c)
Begründe, dass der Wert des Terms  nur von der Seitenlänge der Grundfläche abhängt.
nur von der Seitenlänge der Grundfläche abhängt.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung P1
a)
Der Graph der Funktion hat die Form einer nach oben geöffneten Parabel. Der Scheitelpunkt entspricht somit dem Tiefpunkt des Graphen.
1. Schritt: Ableitungen bestimmen

 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/6345ee8a84cc74380168f5b10b3a87fc68e4210bc81fbab20e2af49f8987a4f1?color=5a5a5a) 3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 4. Schritt:
4. Schritt:  -Koordinate bestimmen
-Koordinate bestimmen
![\(\begin{array}[t]{rll}
f(3)&=&3^2 - 6 \cdot 3 & \\[5pt]
&=& -9
\end{array}\)](https://mathjax.schullv.de/9714ff39f88532054fea28d0b079330e8ba21ceacf34e731b56667ef582c4cfb?color=5a5a5a) Die Koordinaten des Scheitelpunkts ergeben sich zu
Die Koordinaten des Scheitelpunkts ergeben sich zu 
b)
Die allgemeine Tangentengleichung lautet 
 -Koordinate von
-Koordinate von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
f(-2)&=& (-2)^2-6 \cdot (-2)& \\[5pt]
&=& 16
\end{array}\)](https://mathjax.schullv.de/3f7b978eec0fbd2361883ba6017054aa9779880f663244d38f47d08ffbd38471?color=5a5a5a) Steigung
Steigung  an der Stelle
an der Stelle  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/5d1039e8d8ddcb2e0d92c7cc627301ea514ea4e63255a40121da1a91e13266c5?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in die allgemeine Tangentengleichung ergibt:
in die allgemeine Tangentengleichung ergibt:
![\(\begin{array}[t]{rll}
16&=& -10 \cdot (-2) +b&\quad \scriptsize \mid\; -20 \\[5pt]
-4&=& b
\end{array}\)](https://mathjax.schullv.de/f02cffcd0c5455b275de6d545024343eed91c0d313f0728e15c0dbeb710b3e64?color=5a5a5a) Somit gilt
Somit gilt  und die Tangentengleichung im Punkt
und die Tangentengleichung im Punkt  folgt mit
folgt mit 
Lösung P2
a)
Graph II kommt nicht in Frage, da  für
für ![\(x \in [0;1]\)](https://mathjax.schullv.de/d7d1a396bf6537b829aa4ae286cf2c87dea443a40ebf247503ba73ce2f965908?color=5a5a5a) und somit im gegebenen Intervall
und somit im gegebenen Intervall  . Im Intervall
. Im Intervall ![\([0,1]\)](https://mathjax.schullv.de/463f2998327eb3a694145e6014444480b2235be84aa6cfd57871cc64f1cd816c?color=5a5a5a) liegt der Graph II jedoch über der
liegt der Graph II jedoch über der  -Achse.
Graph III kommt nicht infrage, da die Steigung des Graphen von
-Achse.
Graph III kommt nicht infrage, da die Steigung des Graphen von  für
für  nicht konstant ist.
nicht konstant ist.
b)
Die Fläche, die der Graph von  und die
und die  -Achse einschließen, liegt im Intervall
-Achse einschließen, liegt im Intervall ![\([-1;1].\)](https://mathjax.schullv.de/9ee67de6e588cb24ee4b89dc565addcb1a258582df85bf2ff7e5546ef182ff1a?color=5a5a5a) Da der Graph der Funktion punktsymmetrisch zum Ursprung ist, wird der Flächeninhalt der Fläche wie folgt berechnet:
Da der Graph der Funktion punktsymmetrisch zum Ursprung ist, wird der Flächeninhalt der Fläche wie folgt berechnet:

![\( = 2 \left[\dfrac{1}{4}x^4 - \dfrac{1}{2} x^2 \right]_{-1}^0 \)](https://mathjax.schullv.de/262294b60ad3a6bfa166002095dcae666840cce693958177def7568f447bee0d?color=5a5a5a)

![\(= \dfrac{1}{2}\,[\text{FE}]\)](https://mathjax.schullv.de/09e4dc03abe8acb13dad75145b4b5e6fcacdf606007ee4729743f6352f7dc2ec?color=5a5a5a)
Lösung P3
a)
b)
Lösung P4
a)
b)
Damit das Dreieck im Punkt  eine rechten Winkel hat, muss
eine rechten Winkel hat, muss  senkrecht zu
senkrecht zu  sein, also
sein, also 






Für ist
ist  und das Dreieck
und das Dreieck  damit im Punkt
damit im Punkt  rechtwinklig.
rechtwinklig.
Für
Lösung P5
a)
Der Punkt liegt auf halber Strecke zwischen den Punkten  und
und 
b)
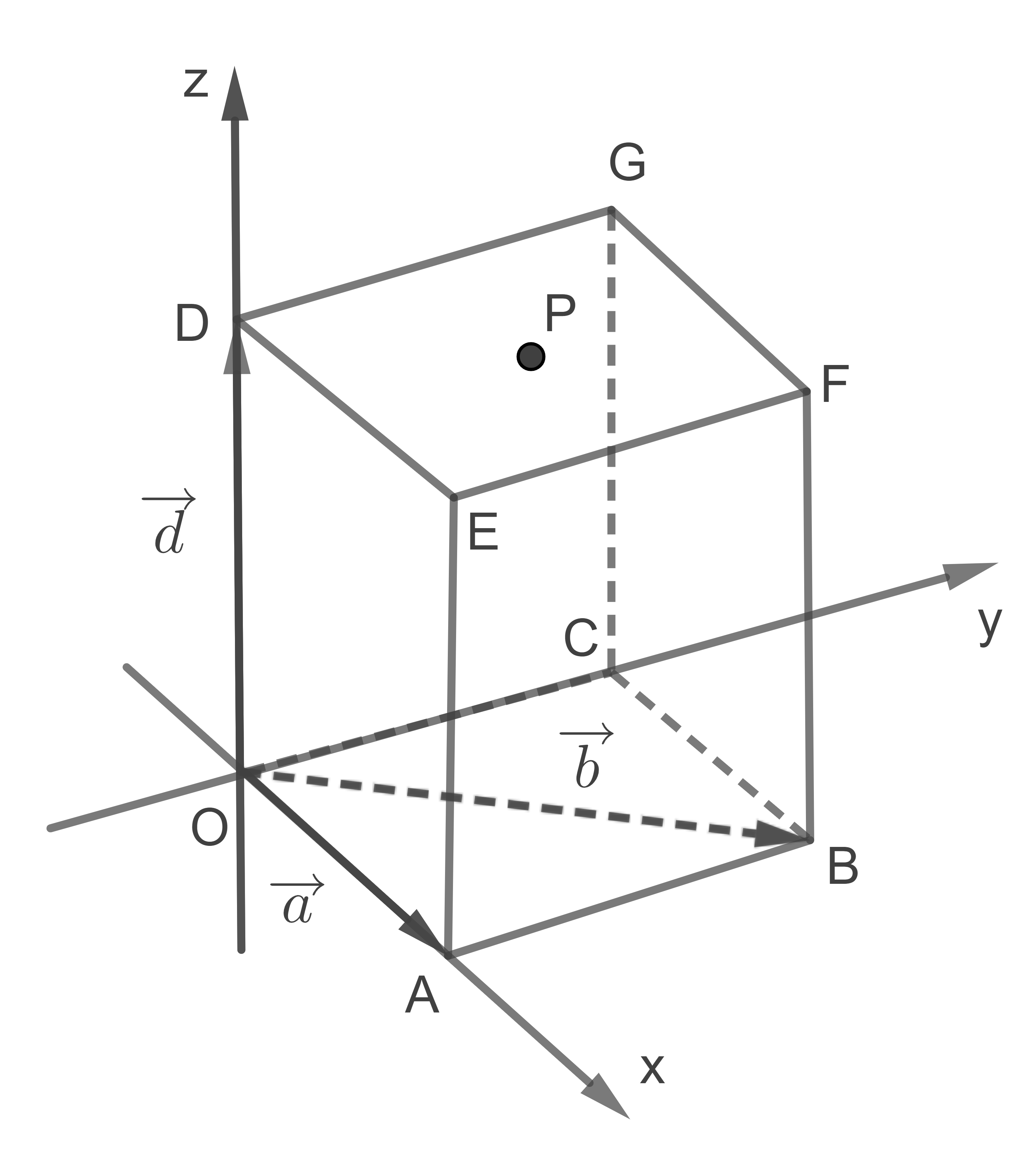
c)
Der Wert von  hängt von den Seitenlängen der Grundfläche ab, denn es gilt der Zusammenhang
hängt von den Seitenlängen der Grundfläche ab, denn es gilt der Zusammenhang  , wobei
, wobei  und
und  die Seiten der Grundfläche sind.
Weiter gilt
die Seiten der Grundfläche sind.
Weiter gilt 
 Da
Da  orthogonal zu
orthogonal zu  steht, gilt
steht, gilt  Daraus folgt
Daraus folgt  und somit hängt der Wert von
und somit hängt der Wert von  nur von der Seitenlänge der Grundfläche ab.
nur von der Seitenlänge der Grundfläche ab.